構建“培養幾何直觀能力”的練習課
——“圖形與幾何”練習課教學改進與創新有感
浙江省余姚市實驗學校 孫 潔
構建“培養幾何直觀能力”的練習課
——“圖形與幾何”練習課教學改進與創新有感
浙江省余姚市實驗學校 孫 潔
“圖形與幾何”(測量)領域的練習課設計,除了讓學生掌握“四基”外,更為重要的是通過練習培養學生的幾何直觀能力,發展學生的空間觀念。學會用圖形思考、想象問題是研究數學,也是學習數學的基本能力,這種能力的培養要貫穿于數學教學的全過程,而練習課則是一個重要的戰場。
練習課;幾何直觀
在2011版課程標準頒布后,又開展了一輪“以學為中心”的課改攻堅戰,在這樣的背景下,小學教學課程及教學的研究將逐步深入并細微化,小學教學課堂中教學的方式方法發生了巨大的變化,從教師主宰課堂到教師的教與學生的學的統一;從教師講學生聽到豐富而有效的數學教學活動;從重視知道結論到重視為學生提供充足的時間和空間經歷觀察、實驗、猜測、計算、推理、驗證等活動過程;課堂教學目標從落實“雙基”到落實基本知識、基本技能、基本思想和基本活動經驗的“四基”等等。但當我們仔細品味其中時卻不難發現,這一系列的改變更多指向的是數學教學中的新授課,而對于作為新授課補充與延續的練習課相比之下卻少有人問津。
這些年,筆者進行了“圖形與幾何”(測量)領域練習課教學改進與創新的實踐,下面談談粗淺的經驗。
一、練習課改進與創新的實踐目標
構建“基于培養幾何直觀能力的練習課”是本次課堂研究的實踐目標。幾何直觀主要是指利用圖形描述和分析數學問題。借助幾何直觀可以把復雜的數學問題變得簡明、形象,有助于探索解決問題的思路,預測結果。“圖形與幾何”(測量)領域的練習課設計,除了讓學生掌握“四基”外,更為重要的是通過練習培養學生的幾何直觀能力,發展學生的空間觀念。學會用圖形思考、想象問題是研究數學,也是學習數學的基本能力,這種能力的培養要貫穿于數學教學的全過程,而練習課則是一個重要的戰場。要摒棄以訓練解題能力、獲取解題技巧為目的的設計理念,而應結合學生的實際,設計針對的題型,有利于學生的想象和操作,進而培養學生的幾何直觀。
二、練習課改進與創新的理論基礎
基于“培養幾何直觀能力”的練習課的改進與創新需要實踐研究的理論基礎。建構主義理論和“做中學”理論能有效地指導練習課的改進與創新。
建構主義理論是學習理論認識心理學派的一個分支,它是行為主義發展到認知階段后的進一步發展。建構主義認為人們通過個人的經歷和圖式來不斷地建構個體對世界的認識,因此強調培養學習者在真實的情境中進行問題解決。建構主義理論強調:①學習是學習者主動建構內部心理表征的過程。②學習的建構過程包含兩方面的建構,即對新信息意義的建構和原有經驗的改造和重組,使學習者為自己的“經驗流”建立一種秩序。③學習者以自己的方式建構對事物的理解,從而不同的人看到的是事物的不同方面,因此要增進學生之間的交流與合作,提倡合作學習。
“做中學”最早由美國著名教育家杜威提出,在歷史發展過程中,研究者賦予了“做中學”更多的價值與內涵。美國著名教育家杜威提出了經驗主義教育思想,為操作學習提供了理論基礎和實踐雛形。“做中學”的理念就在于“我聽了,我忘了;我看了,我記住了,我做了,我明白了”,這種理念強調學生親身經歷的探索過程,通過自己觀察、提問、假設、驗證等活動,體驗探索知識的過程,建構知識體系、形成一定的探究能力,積累活動經驗和探究經驗。
三、練習課改進與創新的基本模式
結合研究目標,本次實踐重點研究了基于“培養學生幾何直觀能力”的練習課教學的基本流程與操作范式,初步建立練習課的課堂教學的基本模式,如下圖:
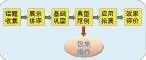
以六年級下冊《圓錐的體積》練習課為例,具體如下:
①收集錯例——這是課堂教學前的環節。教師依據新授課的教學內容,組織進行前測或審閱學生的作業本,收集相關典型的錯題。
②展示講評——結合學生的錯題匯總,引導學生先進行自我解剖:這些題目錯在哪里?為什么會產生這樣的錯誤?應該怎樣改正?這個環節為下一步的練習進行知識上的自我回顧和糾正。

通過學生錯例的展示,讓學生思考錯誤的原因,由于錯誤資源來源于學生,因此可以激發學生學習的主動性。通過錯例原因的反思,不但給了錯誤學生再次回顧圓錐體積計算方法的機會,而且讓全體學生進一步體驗到良好的學習習慣的重要性。
③基礎鞏固——以全班學生為目標,設計基礎性的習題,鞏固學生的基礎知識,培養基本技能,以達到保底的目標。



④典型練習——這是課堂教學中的主要環節,結合數學知識點,以培養學生的幾何直觀能力為核心目標,設計出相關的習題,便于學生進行空間想象和動手操作,以此達到課堂的教學目標。

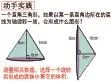
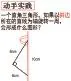
培養學生的“幾何直觀”是圖形與幾何教學的核心理念,而想象和畫圖是培養學生幾何直觀能力有效的途徑之一。從一個平面的直角三角形入手,讓學生先想象旋轉后的圖形的形狀,再畫出這樣的立體圖形,進而選擇一個圓錐進行體積的計算,這樣的設計不但進一步鞏固了圓錐體積的計算方法,而且有效地培養了學生的空間觀念,學生的思維從一維空間發展到二維空間。同時,沿斜邊旋轉和鈍角三角形的旋轉提升了思維的含量,激發了學生的探索欲望。
⑤應用拓展——這不是數學知識點的簡單重復練習,而是對原先學習過的內容進行綜合提升后的練習,是一個使學生對所學知識達到深入理解、融會貫通、牢固掌握,提高數學知識應用能力和技能的過程,更是學生獲取解題的不同策略,感悟數學思想方法,提高解決實際問題能力的重要環節。

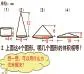

新課標指出“學會用圖形思考、想象問題是研究數學,也是學習數學的基本能力,這種能力的培養要貫穿于數學教學的全過程。”因此,設計練習題時讓學生根據提供的信息先想象出這個立體圖形,再畫出這個立體圖形,就是把頭腦中的幾何形象進行物化,這是一種培養學生幾何直觀的有效方法。而在比較圖形體積的過程中,允許不同的學生運用不同的方法進行解答,不但尊重了學生作為學習主體的地位,更讓學生積累了解決問題不同策略的數學活動經驗。把學生課堂生成的信息匯總成表,讓學生進行觀察探索,培養了學生的分析、推理和綜合的能力,溝通了圓柱和圓錐體積計算之間的內在聯系,更突出了體積與底面積和高之間的關系。及時的應用提升既鞏固了學生發現的數學規律,又激發了學生探索數學的欲望。
⑥效果評價——這是一個完整教學的階段性總結環節,主要由教師對個人自身的教學活動進行客觀的自我評價,另外也要完成對學習者個人的學習評價。
綜上所述,圖形與幾何的練習課的改進和創新,需要建立新的課堂教學模式,關注學生的數學核心素養,設計針對性的有利于學生想象和操作的練習題,在學生動手、動腦、動口的過程中培養學生的幾何直觀能力,發展學生的空間觀念,做到“下要保底,上不封頂”,最終達到改變學習方式、提升學生的數學綜合素養的目的。
[1]義務教育數學課程標準:2011年版[S].北京:北京師范大學出版社,2012(1).
[2]朱榮武.小習題 大習題[J].小學數學教師,2015(6):67.
[3]張佩玲,呂傳漢.小學數學核心概念教學研究[M].貴陽:貴州人民出版社,2008(12):36-54.

