強G-預不變凸函數
李 婷
(山西大學商務學院 基礎教學部,太原 030031)
強G-預不變凸函數
李 婷
(山西大學商務學院 基礎教學部,太原 030031)
主要以強G-預不變凸函數為研究對象,首先在中間點的G-預不變凸性下得到了G-預不變凸函數的一個判定定理,然后將已有文獻的結果進行了推廣,得到了在中間點的強G-預不變凸性下強G-預不變凸函數的兩個重要的判定定理。
強G-預不變凸函數;嚴格G-預不變凸函數;半嚴格G-預不變凸函數
0 引言
在研究最優化問題時,凸性和廣義凸性起著很重要的作用。近年來,國內外很多學者將凸函數不斷進行推廣,得到了一系列的廣義凸函數及其相關成果,具體見參考文獻[1-8],這些文獻詳細介紹了不變凸性、預不變凸性、強預不變凸性、G-預不變凸性、強G-預不變凸性等,并給出了這些廣義凸函數的性質。
2011年,彭再云等在文獻[8]中給出了強G-預不變凸函數的如下的一個判定定理。
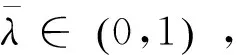
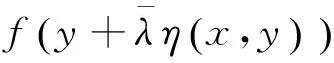
本文首先得到了半嚴格G-預不變凸函數是G-預不變凸函數的一個充分條件,然后將上述引理的結果進一步推廣,得到了強G-預不變凸函數的另外兩個判定定理。
1 基本知識
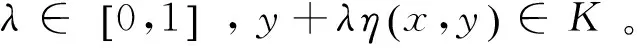

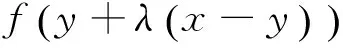
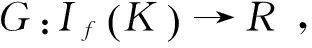
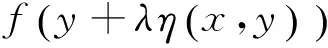
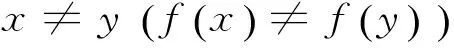
時上述不等式嚴格成立,即:
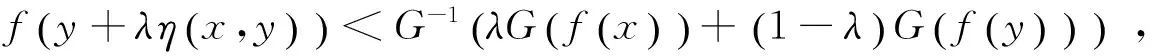
定義4[8]設集合K?Rn是關于η:Rn×Rn→Rn的不變凸集,f:K→R是定義K上的函數,稱f是K上關于η的強G-預不變凸函數,如果存在連續遞增函數:
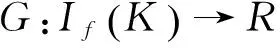
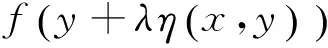
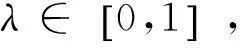
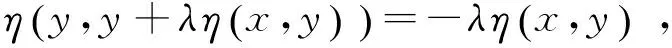
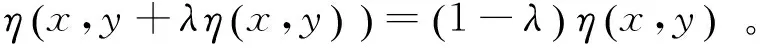
2 半嚴格G-預不變凸函數是G-預不變凸函數的一個充分條件
引理2.1 設G:R→R是一個連續實值函數,則G-1是遞增函數當且僅當G也是遞增函數。
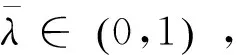
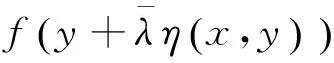
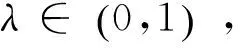
(1)
因為G單調遞增,由引理2.1可知,G-1也是單調遞增的。
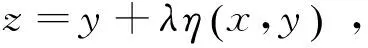
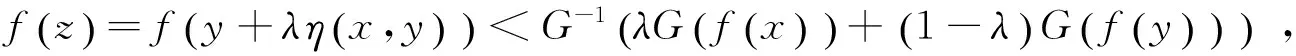
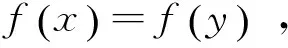
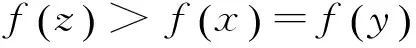
(2)
(3)
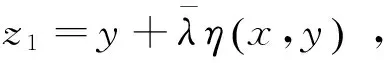
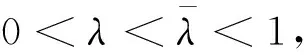
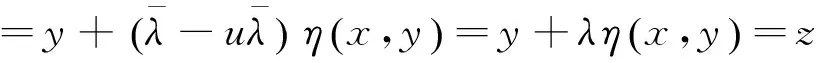
由f的半嚴格G-預不變凸性,引理2.1及(3)式可得:
上式與(2)式矛盾。
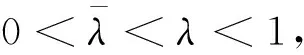
由f的半嚴格G-預不變凸性,引理2.1及(3)式可得:
上式與(2)式矛盾。故假設不成立,所以f是K上關于η的G-預不變凸函數。
3 強G-預不變凸函數的兩個判定定理
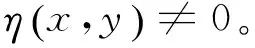
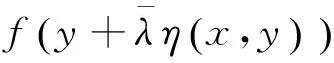
(4)
則f是K上關于η的強G-預不變凸函數。
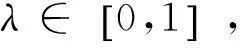
(5)
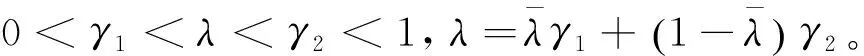
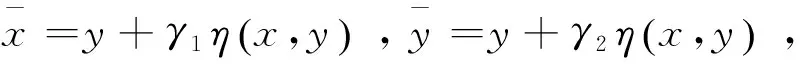
(6)
由條件C可得:
(7)
(8)
由(4)和(7)式可得:
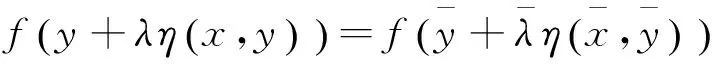
(9)
又由(6)式有:
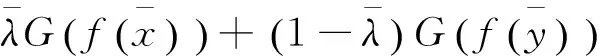
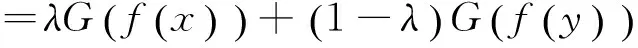
(10)
所以,由(8)、(9)及(10)式可得:
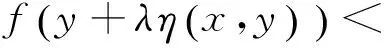

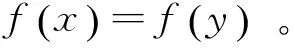
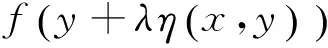
于是,f是K上關于η的強G-預不變凸函數。
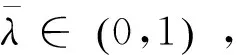
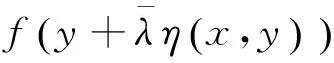
(11)
則f是K上關于η的強G-預不變凸函數。
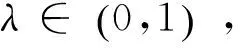
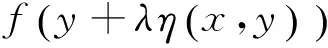
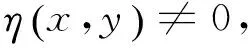
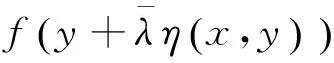
(12)
由定理2.1及(12)式知f是K上關于η的G-預不變凸函數,從而由引言中的引理得,f是K上關于η的強G-預不變凸函數。
[1]CravenBD.Invexfunctionsandconstrainedlocalminima[J].BulletinoftheAustralianMathematicalSociety, 1981, 24(3):357-366.
[2]WeirT,MondB.Preinvexfunctionsinmultipleobjectiveoptimization[J].JournalofMathematicalAnalysis&Applications, 1988, 136(1):29-38.
[3] 顏麗佳, 劉芙萍. 強預不變凸函數[J]. 重慶師范大學學報(自然科學版), 2005, 22(1):11-15.
[4]SchaiblesT,ZiembaWT.Generalizedconcavityinoptimizationandeconmics[M].London:AcademicPress, 1981.
[5]AntczakT.G-pre-invexfunctionsinmathematicalprogramming[J].JournalofComputational&AppliedMathematics, 2008, 217(1):212-226.
[6]AntczakT.NewoptimalityconditionsanddualityresultsofGtypeindifferentiablemathematicalprogramming[J].NonlinearAnalysis, 2007, 66(7):1617-1632.
[7]LuoHZ,WuHX.OntherelationshipsbetweenG-preinvexfunctionsandsemistrictlyG-preinvexfunctions[J].JournalofComputational&AppliedMathematics, 2008, 222(2):372-380.
[8] 彭再云, 房效亮, 趙勇. 強G-預不變凸函數[J]. 重慶師范大學學報(自然科學版), 2011, 28(6):7-10+18.
責任編輯:程艷艷
StrongG-PreinvexFunctions
LITing
(FundamentalTeachingDepartment,BusinessCollegeofShanxiUniversity,Taiyuan030031,China)
Taking strongG-preinvexfunctionastheresearchobject,thispaperobtainsajudgingtheoremofG-preinvexfunctiononthemiddlepointofG-preinvexity,andthengeneralizestheresultsoftheexistedliterature,finally,obtainstwoimportantjudgingtheoremsofstrongG-preinvexfunctiononthemiddlepointofstrongG-preinvexity.
strongG-preinvexfunction;strictG-preinvexfunction;semi-strictG-preinvexfunction
2017-02-18
山西省教育科學“十三五”規劃課題(GH—16713);山西大學商務學院科研項目(2016027)
李婷(1981-),女,山西永濟人,講師,碩士,主要從事最優化理論及應用方面研究。
O
A
1009-3907(2017)04-0025-04

