單抽汽輪機熱電耦合的模糊解耦控制

李 艷， 拓福婷， 劉麗芳

(1.陜西科技大學 電氣與信息工程學院， 陜西 西安 710021； 2.陜西農產品加工技術研究院， 陜西 西安 710021； 3.陜西科技大學 職業教育師范學院， 陜西 西安 710021)

?

單抽汽輪機熱電耦合的模糊解耦控制

李 艷1,2， 拓福婷1， 劉麗芳3

(1.陜西科技大學 電氣與信息工程學院， 陜西 西安 710021； 2.陜西農產品加工技術研究院， 陜西 西安 710021； 3.陜西科技大學 職業教育師范學院， 陜西 西安 710021)

抽汽式汽輪機存在著熱負荷、電負荷之間的強耦合以及參數的不確定性問題，其中任一負荷的變化都會引起另一個的波動，進而影響整個汽輪機控制系統的性能.針對上述問題，以某造紙廠熱電廠6 MW單抽汽輪機為例，在分析其工作原理的基礎上應用機理法建立了系統數學模型.其次，分析了其強耦合特性，根據實際需要設計了模糊解耦控制方法以實現熱電解耦及提高系統適應性.最后，進行了Matlab/Simulink仿真實驗，結果表明，與常規對角解耦相比，該方法在強耦合及模型參數存在一定波動時，仍能保證較好的穩定性及魯棒性.

汽輪機; 熱電負荷耦合; 數學模型; 模糊解耦控制

0 引言

抽汽式汽輪機是一類既能供熱又能供電的原動機械，是目前實現熱電聯產的主要形式之一，具有能源利用合理，循環熱效率高、運行方式靈活、適用范圍廣的特點，因此受到廣泛的重視和應用，主要包括化工、造紙、發電等行業[1,2].但抽汽式汽輪機結構復雜，存在強熱電耦合特性，為保證供熱和供電品質，就要選擇合適的控制方案及控制器參數.因此，實現汽輪機熱電解耦控制具有十分重要的意義，也是目前研究的重點問題之一[3].

針對抽汽式汽輪機熱電強耦合特性引起的系統輸出頻繁波動的問題，國內外許多科研機構和高校進行了大量的理論分析和實驗研究[2-6].文獻[2]將功率變化對熱負荷的影響通過加權系數疊加在控制熱負荷變化的閥門上，來消除熱電耦合，其本質是對角解耦.雖然實現了系統靜態解耦，但嚴重依賴于解耦系數的準確性.文獻[3]提出了分塊線性化的熱-電負荷比例解耦控制算法，并給出了基于非線性工況圖的比例系數計算方法.該方法能夠實現系統靜態解耦及準動態解耦，但存在對系統非線性工況圖準確性要求較高的問題.文獻[4]提出利用電液控制電信號處理方便的優點實現系統電負荷與熱負荷的解耦，但也要求精確的數學模型，不適用于含有不確定性參數的系統.文獻[5,6]以某小型雙抽汽輪機為被控對象，建立了其動態數學模型，用BP神經網絡實現其解耦控制并提出了基于模糊神經網絡的雙抽汽輪機解耦控制的方法，該方法能夠有效實現熱電解耦控制，但其算法復雜，不易實現.文獻[7,8]應用神經網絡解耦也有相同的問題.

上述方法為汽輪機的解耦控制技術的發展做出了貢獻,但仍然存在一些不足.首先，傳統的對角解耦方法中的解耦系數都是在系統參數確定的情況下，根據多變量解耦理論通過精確計算得到的，對系統精確模型依賴性過高.其次，神經網絡存在需要數據量巨大，訓練時間長等缺點.文獻[9-14]分別將模糊控制理論應用于有各類強耦合系統的解耦控制，雖然方法有所不同但都取得了良好的控制效果，證明模糊控制在解耦控制領域具有一定的優勢.

根據上述分析，本文在完成抽汽式汽輪機機理建模的基礎上，提出了一種PI控制與模糊解耦相結合的控制方法.PI控制具有良好的穩態性能及快速跟蹤性，是一種應用廣泛的控制器.模糊邏輯控制具有不依賴對象精確數學模型、對模型參數變化不敏感以及算法簡單等優點，是處理參數不確定、非線性、多變量強耦合系統的一種有效的方法[14].因此將二者結合，可以在實現系統解耦的基礎上提高系統的適應性、魯棒性.本文以某造紙廠熱電廠6MW汽輪機組為例進行研究，汽輪機是由青島捷能汽輪機集團股份有限公司生產的C6-4.90/0.686單抽汽式汽輪機.

1 系統描述及數學模型的建立

1.1 系統描述

抽汽式汽輪機的詳細模型較復雜，通常在仿真實驗研究中采用較為簡化的結構，典型的單抽汽輪機的結構如圖 1 所示[1].

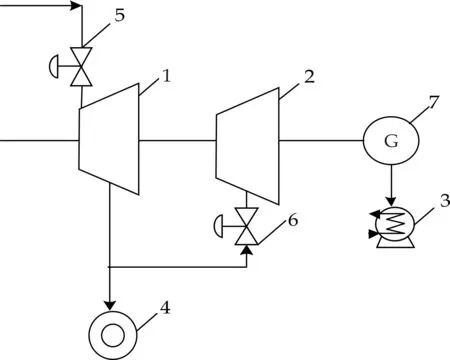
圖1 單抽汽輪機結構

圖1中：1-高壓缸， 2-低壓缸 ，3-凝汽器，4-熱用戶， 5-高壓調節閥 ，6-低壓調節閥 ，7-發電機.這7部分是典型的單抽汽輪機的主要組成環節.其工作原理為：主蒸汽經過高壓調節閥，進入高壓缸，膨脹做功后一部分經低壓調節閥進入低壓缸繼續做功直至凝汽器，另一部分由抽汽口引出到蒸汽容積用于為熱用戶供熱.

當熱負荷增加時，為保證總功率電負荷不發生變化，相應地就要增大高壓調節閥的開度，減小低壓調節閥的開度.同理，當所需的電負荷發生變化時，同時增大高、低壓調節閥的開度，以保證電負荷保持不變.因此通過高、低壓調節閥開度的協調調節就可以同時控制汽輪機總功率及供熱壓力的穩定.

1.2 系統數學模型的建立

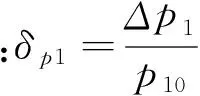
1.2.1 液壓放大元件及執行元件

滑閥油動機是目前廣泛應用的一類液壓放大元件及執行元件，主要包括錯油門、油動機、反饋機構三部分.其輸入量為控制滑閥位移ΔSx，輸出量為油動機活塞位移ΔSz.在不考慮慣性力及初始狀態為平衡狀態的條件下，滑閥油動機模型如圖2所示[1].

圖2 滑閥油動機的傳遞函數框圖

其中，Ks為油動機機構的靜態放大倍數；Th為油動機滑閥時間常數；Ts為油動機時間常數.由于Th?Ts，則滑閥油動機機構的傳遞函數為：

(1)

1.2.2 高、低壓容積方程

單抽汽輪機蒸汽容積分為高壓蒸汽容積和低壓蒸汽容積，高壓蒸汽容積的物理模型如圖3所示.

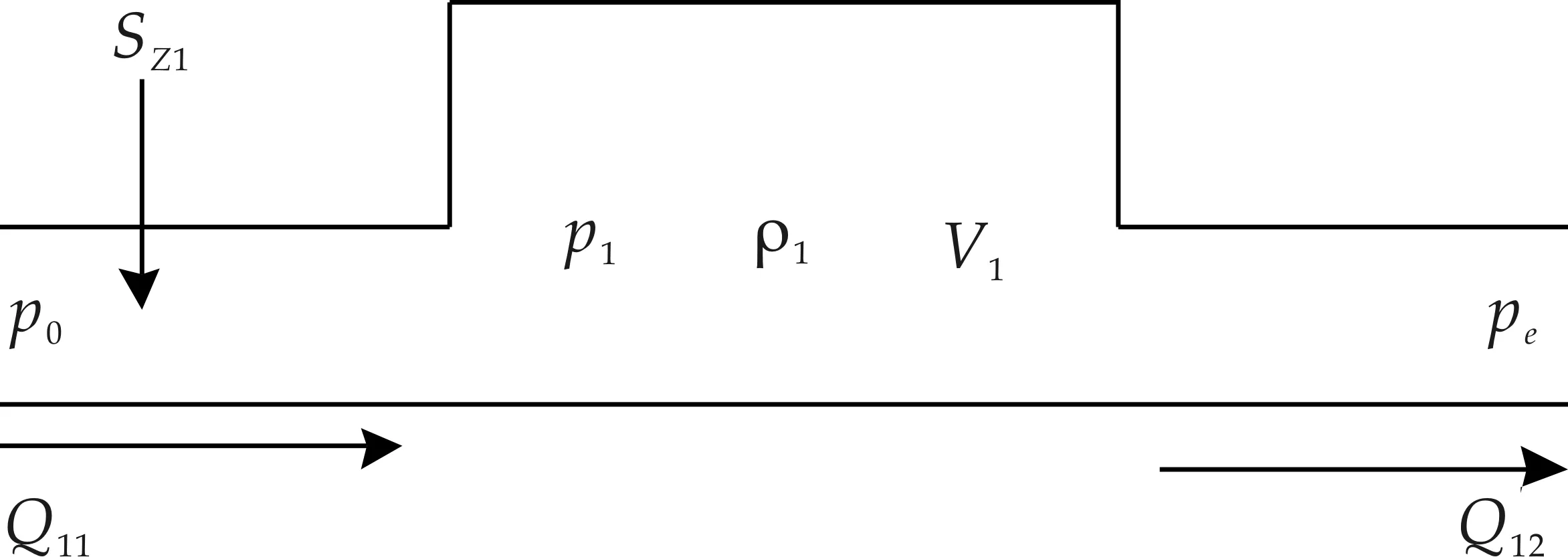
圖3 高壓蒸汽容積物理模型

對于圖3所示的高壓蒸汽容積，在不考慮pe對排汽量Q12影響及p1對進汽量Q11的影響的前提下，Q11主要受p0、Sz1的影響，Q12主要由p1決定.則根據質量守恒定律可得：

(2)

式(2)中：p1、ρ1、V1分別為高壓容積的壓力、密度、體積；Q11、Q12分別為其進汽量、排汽量；p0、pe分別為主蒸汽壓力和抽汽供熱壓力，Sz1為高壓調節閥開度.

設高壓容積的過程為指數為n的多變過程[9]，由氣體多變過程狀態方程可得：

(3)

在工作點(p00、p10、ρ10、Sz10)附近取變化量(Δp0、Δp1、Δρ1、ΔSz1)，考慮額定工況下Q11=Q12，同時有Δp0?p00，Δp1?p10，Δρ1?ρ10,對式(3)進行小偏差線性化處理并將方程中各變量用其相應額定值的百分比表示：

(4)

在假定系統投入運行后主蒸汽壓力不發生較明顯變化的前提下，方程兩邊同時除以Q110對式(4)進行標幺化，則式(4)可簡化為：

(5)

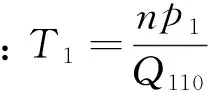
同理，可得低壓蒸汽容積方程為：

(6)

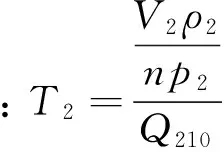
1.2.3 抽汽容積

抽汽容積的物理模型如圖4所示.圖(4)中的低壓容積進汽流量為Q21(不考慮p2對其影響)，主要由受pe和Sz2的影響.Qe由pe和抽汽時間t決定.根據質量守恒定律得：

(7)

式(7)中：pe、ρe、Ve分別為抽汽容積壓力、密度、體積；Q21為低壓容積進汽流量；Qe為供熱蒸汽流量，t為抽汽時間.

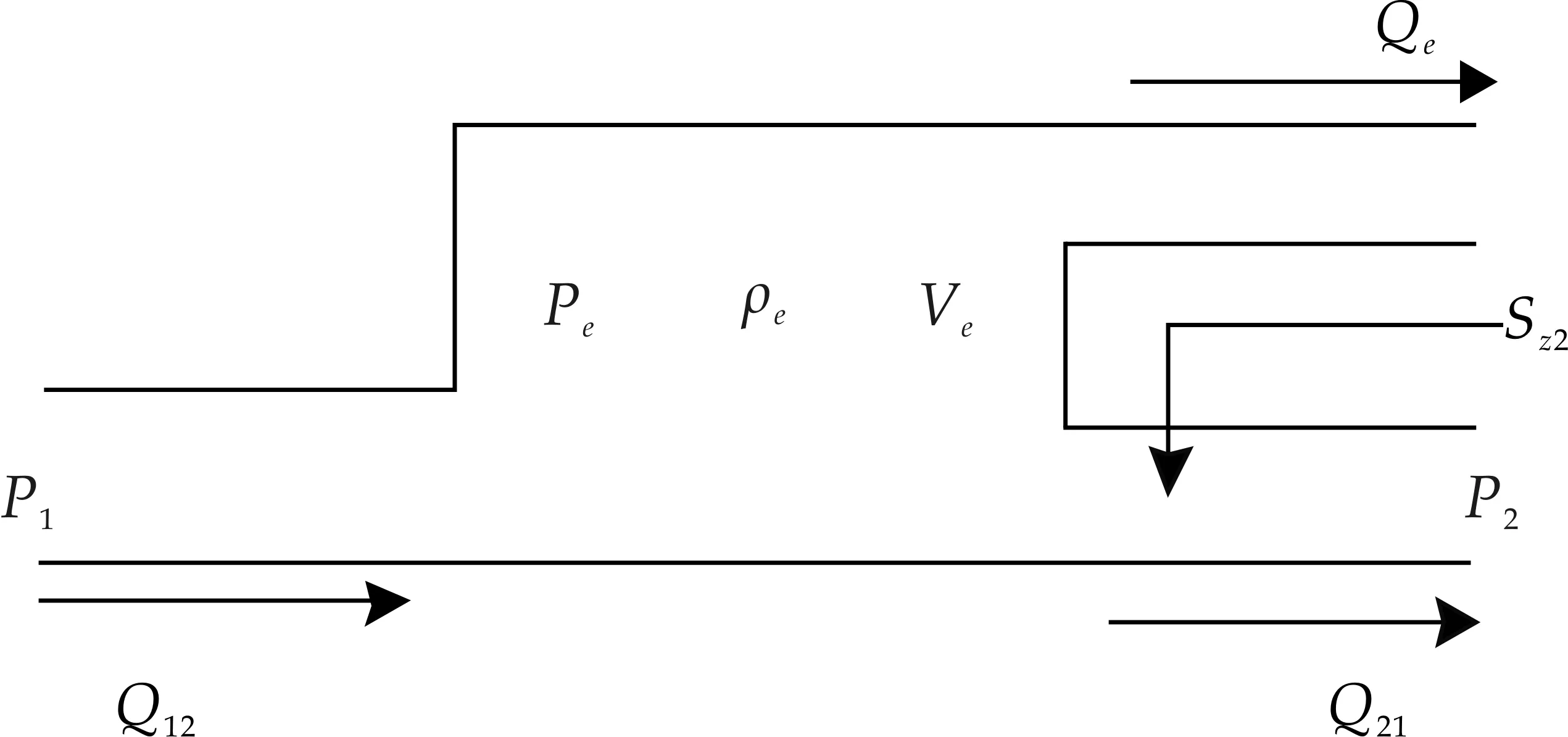
圖4 抽汽容積物理模型

在工作點附近做小偏差線性化(各變量用百分比表示)，取線性部分：

(8)

對式(8)進行標幺化，兩邊同時除以高壓容積排汽量額定值Q120得(此處不考慮熱負荷擾動)：

(9)

1.2.4 轉子方程

汽輪機轉子功率的決定性因素有三個：蒸汽功率NT、負荷消耗功率NL、摩擦功率Nf.則由功率平衡原理可得:

(10)

式 (10)中：J為轉子的轉動慣量，ω為轉子的角速度.Nf為ω的非線性函數，可表示為Nf(ω).NL為電負荷擾動，在進行模型建立時不考慮該擾動. 蒸汽功率：

NT=N1+N2

N1=ΔH1Q12(p1)η1

N2=ΔH2Q22(p2)η2

(11)

式(11)中：N1，N2分別為高壓容積、低壓容積的蒸汽功率；ΔH1、ΔH2和η1、η2分別為高壓缸和低壓缸的焓降和功率因子，建模時，假定其不變.

將式(11)代入式(10)，并對其進行小偏差線性化得：

(12)

對式(12)進行標幺化(不考慮電負荷擾動NL)得轉子方程為：

(13)

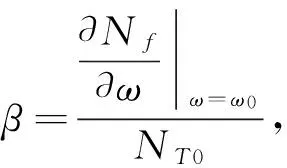
綜上，根據式(1)、(5)、(6)、(9)、(13)，可得單抽汽輪機耦合系統結構圖，如圖5所示(通常假定進汽量與調節閥開度成正比同時進汽量與容積壓力成正比，則k11，k12，k21,k22,ke2,ke3通常均取1).

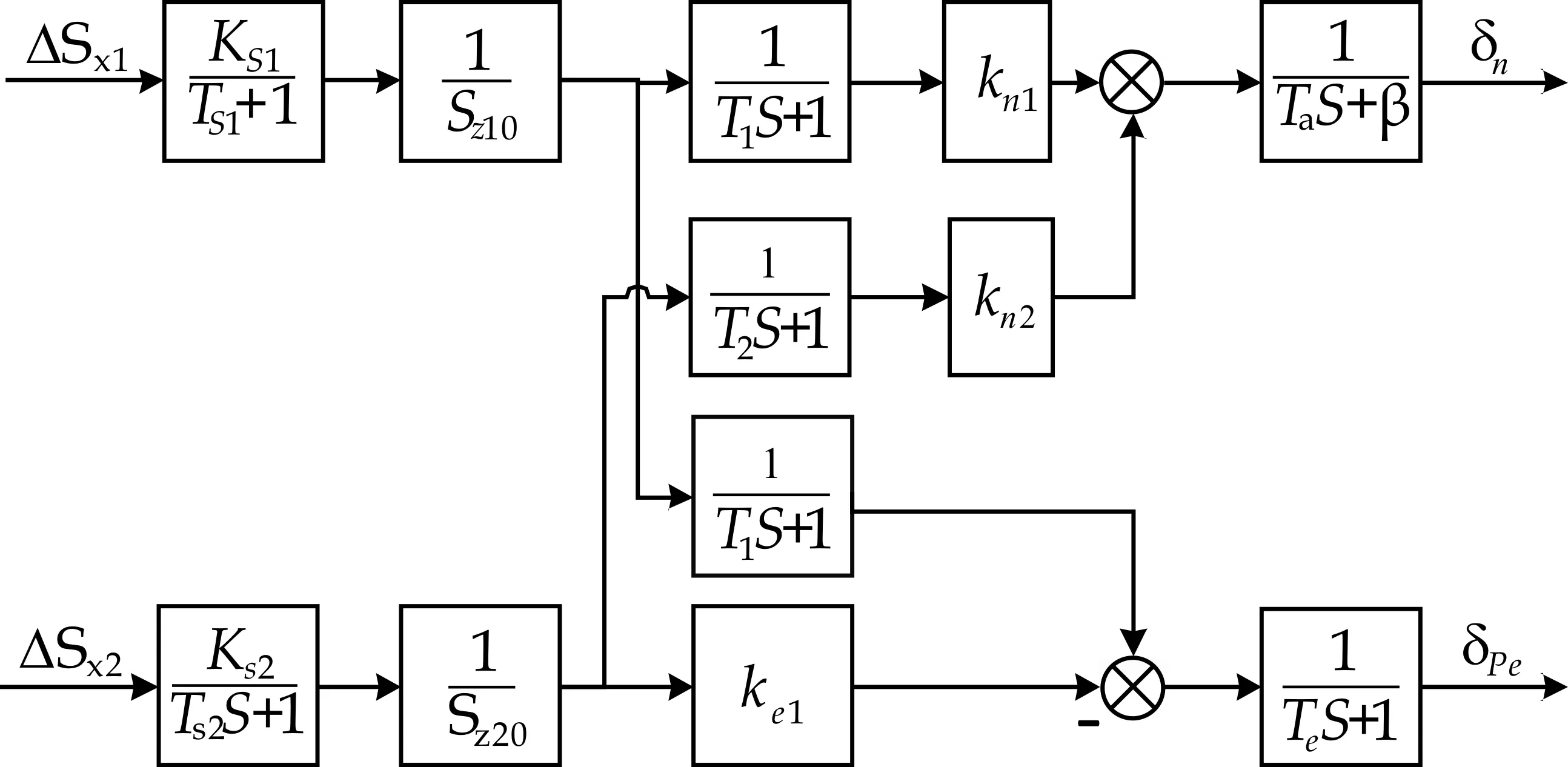
圖5 單抽汽輪機數學模型

其中,Ts1，Ts2分別為兩個控制回路的滑閥油動機時間常數,Ks1、Ks2分別為兩個油動機機構的靜態放大倍數.

2 系統耦合特性分析及解耦控制器設計

2.1 耦合特性分析

多變量系統各回路之間存在耦合，是指系統的某個輸入與系統的所有輸出之間相互影響或系統的某一輸出受所有輸入的影響[15].由上述分析可知汽輪機系統是一個兩入兩出的多變量系統.輸入為高、低壓調節閥的開度，輸出為轉速和抽汽壓力，且高壓、低壓任一調節閥的開度發生變化都會引起兩個輸出量的變化.例如，高壓調節閥開度增大，則汽輪機總功率和抽汽壓力都會增大.因此，汽輪機系統是一個典型的多變量、強耦合系統.

2.2 解耦控制方案結構設計

汽輪機系統解耦控制的目標是實現高、低壓調節閥對汽輪機總功率和抽汽壓力的獨立控制，互不影響.本文提出的模糊解耦控制方案結構框圖如圖6所示.

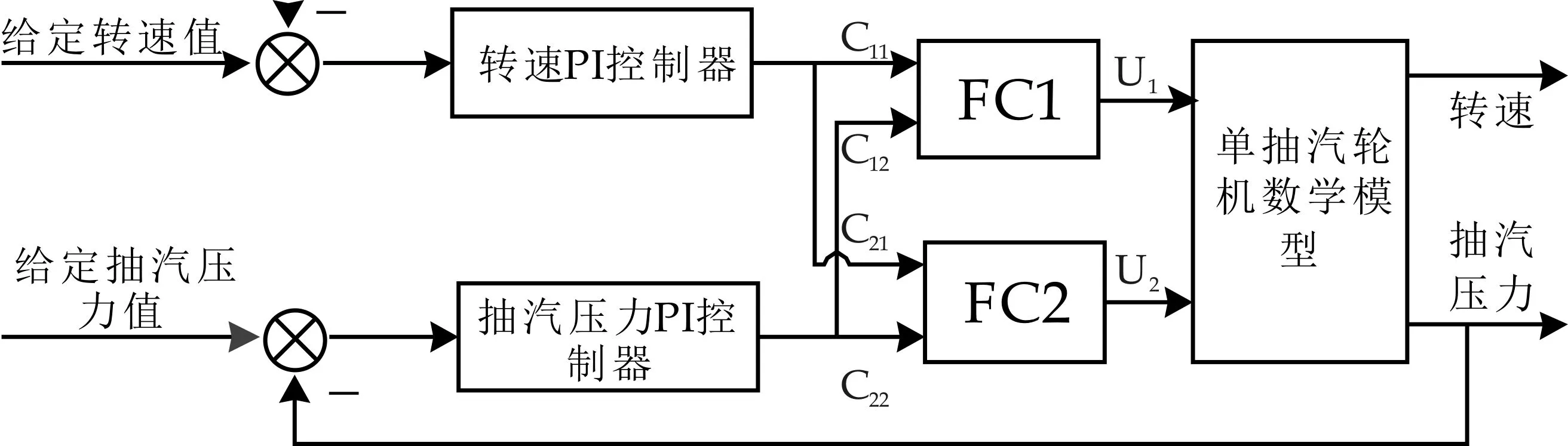
圖6 模糊解耦控制方案結構

解耦方案中，分別用轉速和抽汽壓力表示汽輪機電負荷和熱負荷.其控制原理是：將兩入兩出的多變量耦合系統通過兩個PI控制器和兩個模糊解耦器轉化為兩個兩入單出的控制系統.首先通過模糊解耦器實現系統解耦，然后通過兩個PI控制器依次實現單個回路的控制.

3 模糊解耦器及PI控制器的設計

3.1 模糊解耦器設計

本文采用二維輸入，9*7模糊規則的模糊控制器，由模糊化、模糊推理、解模糊三部分組成.下面以解耦控制器FC1為例進行說明.輸入信號分別為轉速PI控制器輸出信號和壓力PI控制器輸出信號.

(1)模糊變量設計及隸屬度函數選擇

假定模糊控制器的輸入變量分別為C11、C12，論域為[-6,6].輸出變量為U1，其模糊論域為[-10,10].將模糊變量C11、輸出變量U1的論域劃分為9個模糊子集，{NB，NM，NS，NW，Z，PW，PS，PM，PB}，模糊變量C12劃分為7個模糊子集，{NB，NM，NS，Z，PS，PM，PB}.

根據三角形隸屬度函數控制靈敏度高，分辨率高的特點，在PI控制器輸出相對小的時候選用三角形隸屬度函數.同時為了保證系統的穩態性能，在PI控制器輸出值較大時選用S和Z型隸屬度函數，當其輸出值適中時，選用梯形隸屬度函數，即可得模糊解耦器1輸入變量C11的隸屬度函數.依據相似的設計原理，其余各變量的隸屬度函數如圖7所示.

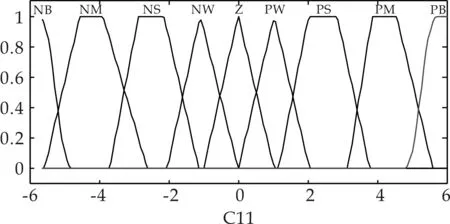
(a)C11的隸屬度函數

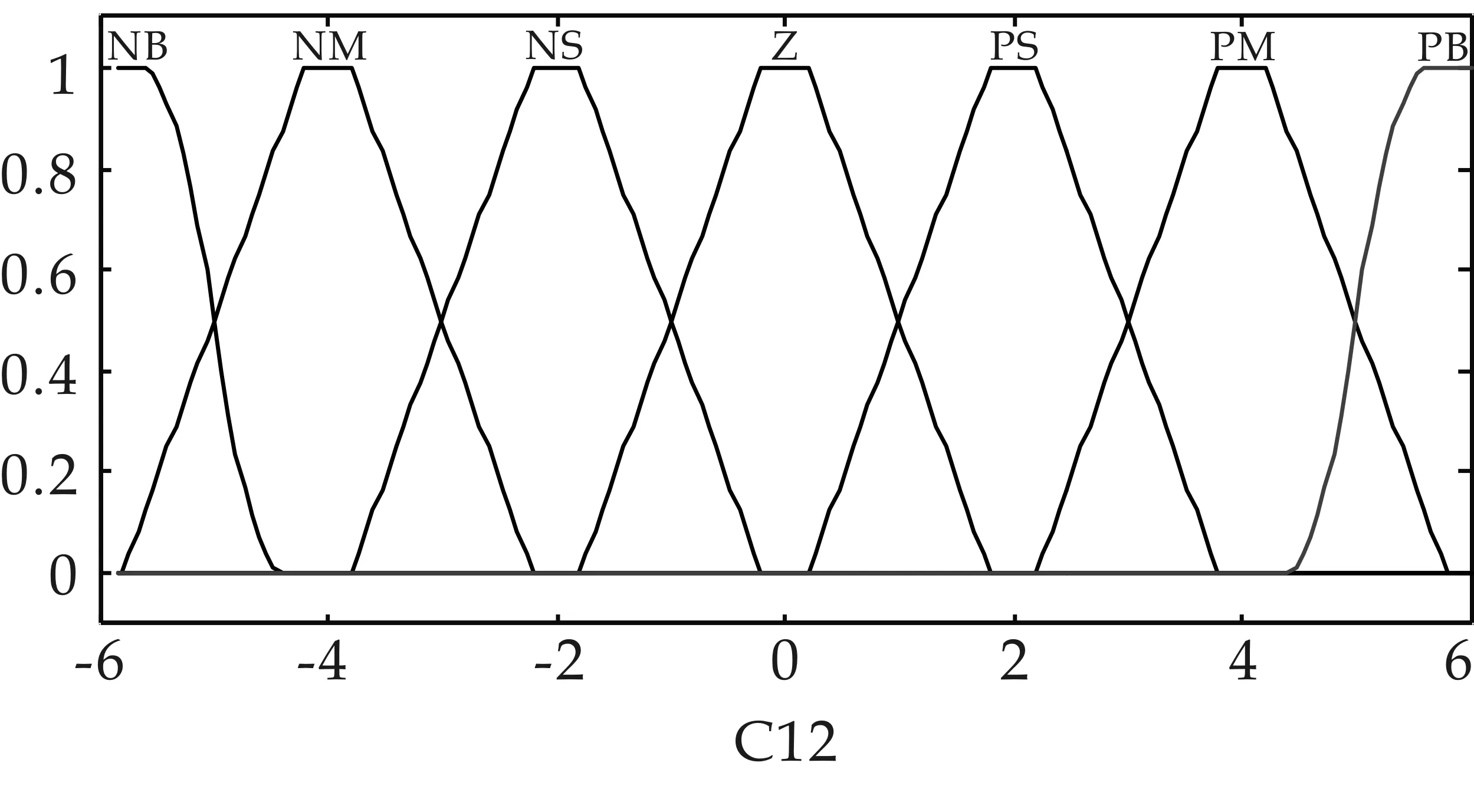
(b)C12的隸屬度函數

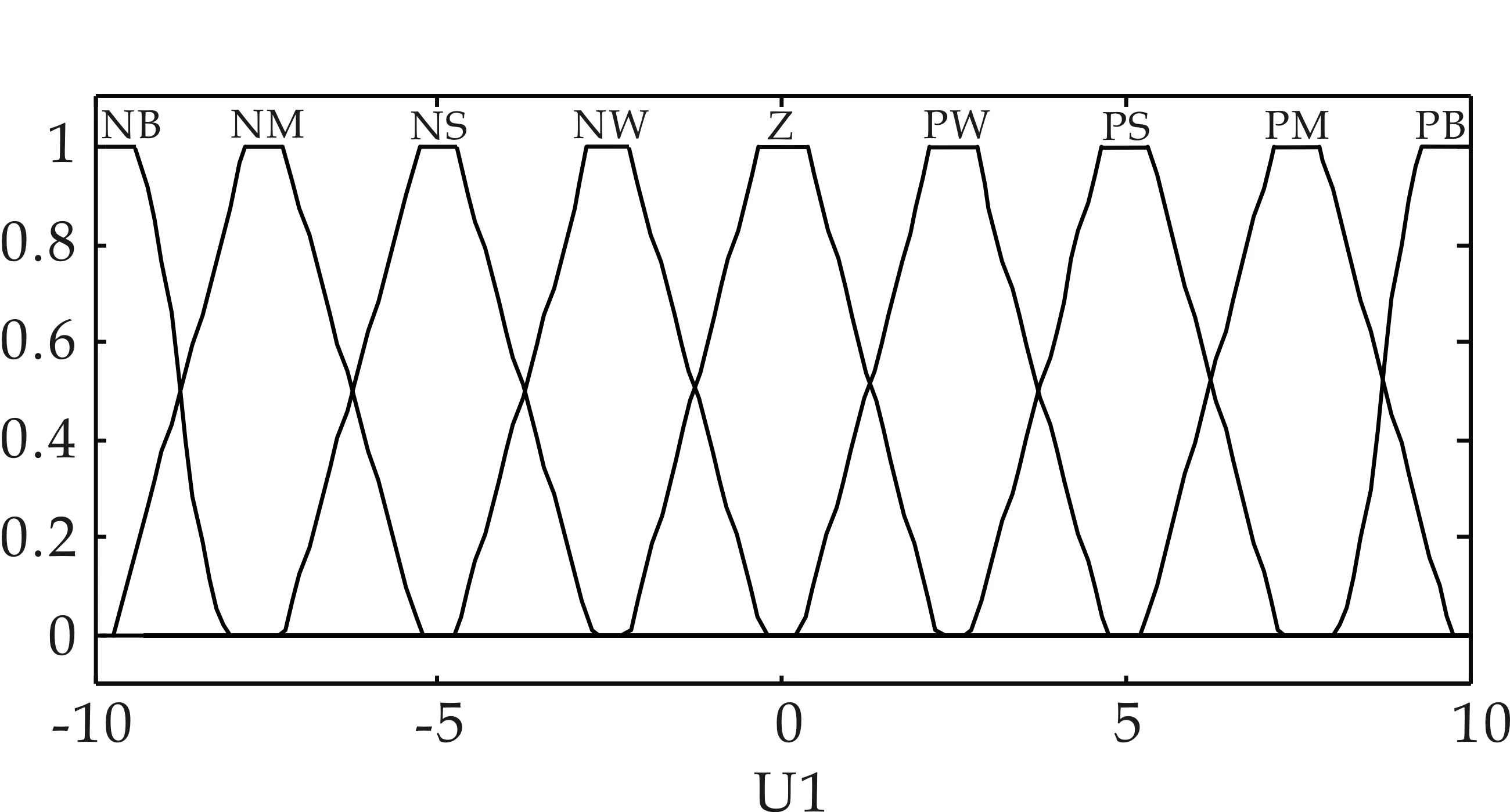
(c)U1的隸屬度函數圖7 模糊解耦控制器1的隸屬度函數

(2)模糊規則設計及解模糊

在本文所設計的模糊解耦控制系統中，模糊控制器的主要作用是解耦，模糊規則根據以下思路建立：當系統電負荷增加時，則系統實際轉速低于設定轉速，如果僅通過增大高壓調節閥的開度來調節，則C11增大，U1增大，調節閥開度增大.但由于耦合關系的存在，此時若C12也增大，則抽汽壓力也低于設定值，根據單抽汽輪機調節原理，則模糊控制器U1應進一步增大.

根據上述思路及實際控制需求，可建立如表1所示的FC1的全部模糊控制規則.

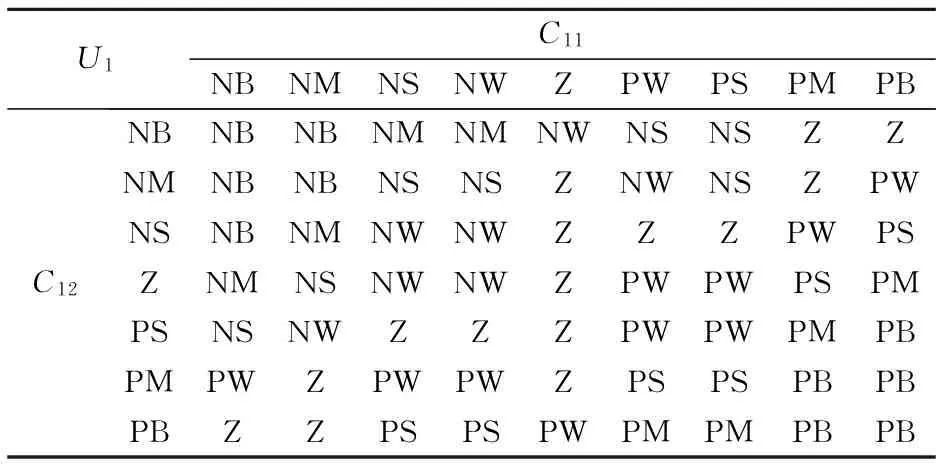
表1 模糊解耦器1的模糊規則表

為獲取準確的控制量，本文選取重心法解模糊方法，其表達式為：

(14)

用類似的方法可完成模糊解耦控制器2的設計.

3.2 轉速及壓力控制器設計

基于PI控制器快速跟蹤輸入，消除靜態誤差的特點，本文選用PI控制器作為轉速和壓力控制器.PI控制器包含比例，積分兩部分，其控制算法如下：

(15)

對于轉速控制回路，系統輸出的轉速經過調速器中的轉速測量元件測量后反饋至系統輸入端，與給定的轉速比較，從而得到轉速PI控制器的輸入信號.壓力PI控制器設計思路同轉速PI控制器.

4 系統仿真實驗

為驗證所設計控制方案的有效性，筆者采用上述6 MW汽輪機組數據進行數字仿真研究，圖5中數學模型的各參數如下：油動機時間常數Ts1=Ts2=0.2，各蒸汽容積時間常數介于0.1～0.3，高壓缸功率系數Kn1=0.6，低壓缸功率系數Kn2=0.4，抽汽流量比Ke=0.4，轉自時間常數Ta=11.8，自平衡系數β=1.

在Matlab/Simulink圖形化建模環境下，根據上述理論分析及實際數據建立如圖8所示的仿真模型.

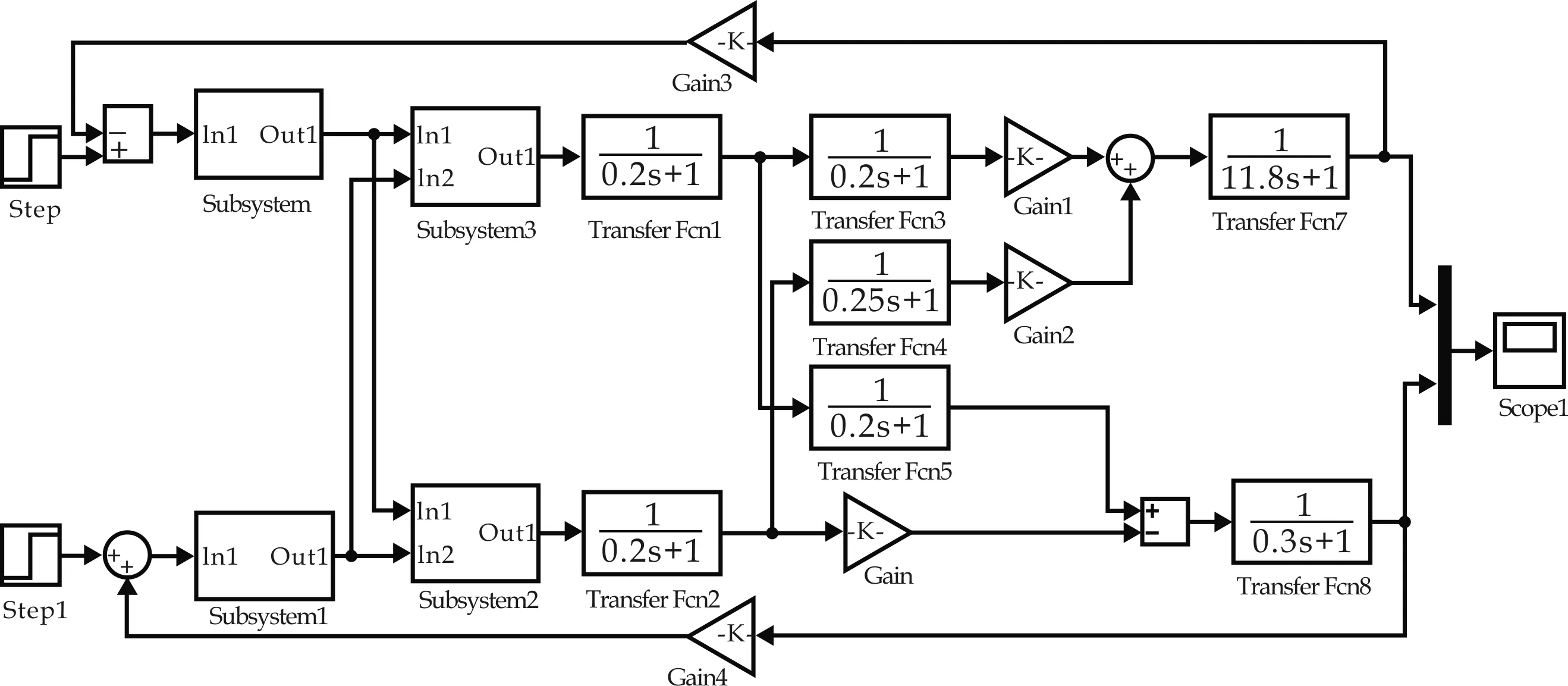
圖8 模糊解耦控制Simulink仿真模型

圖8中各輸入量的量化因子由模糊子集論域的最大絕對值與其基本論域的最大絕對值作商求得，而輸出變量的比例因子由其基本論域的最大絕對值與相應的模糊子集論域的最大絕對值作商得到.根據上述理論計算可得k11=1.5,k12=3,ku1=0.5.具體仿真實驗過程中，通過Matlab/Simulink仿真平臺中Signal Constraints進行調整，得：k11=2,k12=4,ku1=0.65.控制系統中的PI控制器參數可通過試誤法獲得，其中kp1=4.2,ki1=2,Ti1=0.2;kp2=5,ki2=1.2,Ti2=1.1.

仿真實驗中，分別當0 s和20 s時在電負荷控制回路和熱負荷控制回路中加入終值為1的階躍信號，仿真時間為60 s.解耦效果仿真結果如圖9、10所示.其中,圖9為未解耦時的響應曲線，圖10中(a)、(b)分別為模糊解耦控制和對角解耦控制的仿真結果.

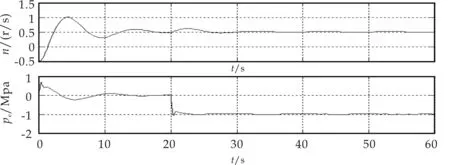
圖9 系統耦合響應曲線

通過對上述仿真結果的分析可知：對于給定的單位階躍輸入信號，采用對角解耦時雖然能夠實現有效解耦但電負荷控制回路輸出的轉速達到了300%的超調，壓力控制回路中，抽氣壓達到了100%的超調.而采用模糊解耦控制時單抽汽輪機系統運行平穩，在電負荷和熱負荷突變時系統輸出波動在3%以內，有效地抑制了汽輪機轉速和抽汽壓力的波動，最終實現了單抽汽輪機系統的高效，快速的解耦控制.

為驗證系統的適應性、魯棒性及抗干擾能力，筆者還根據實際生產情況，就油動機時間常數發生變化及系統加入電負荷擾動的情況作了仿真對比.仿真結果如圖11(a)、(b)、(c)、(d)所示.

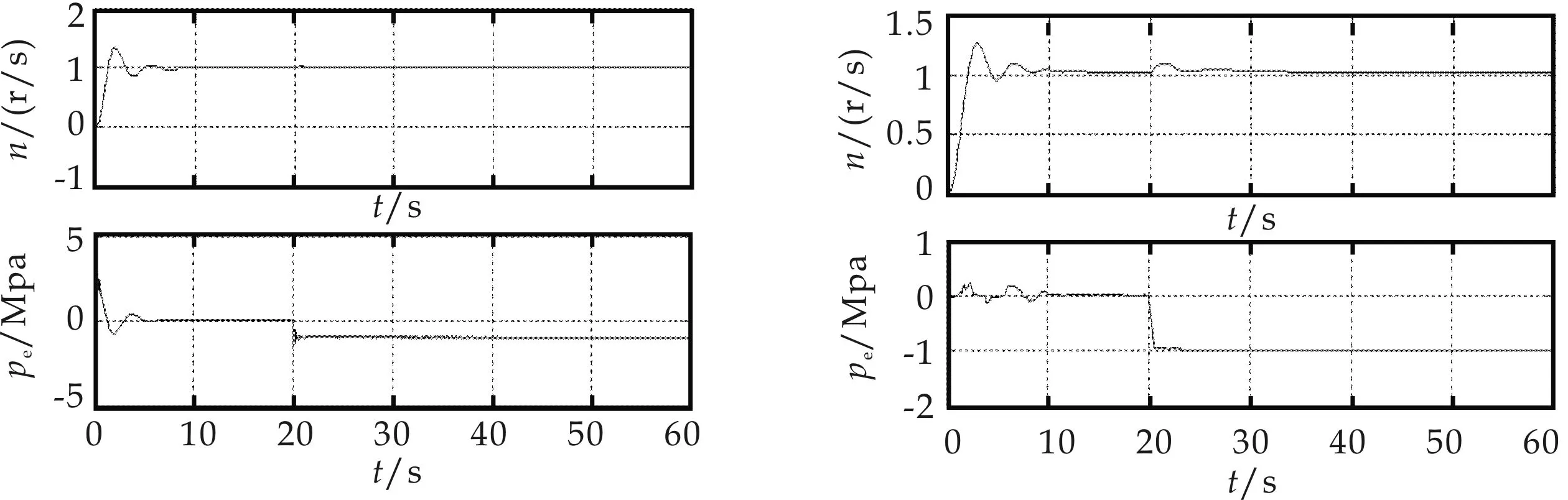
(a)油動機1時間常數變 (b)油動機1時間常數變

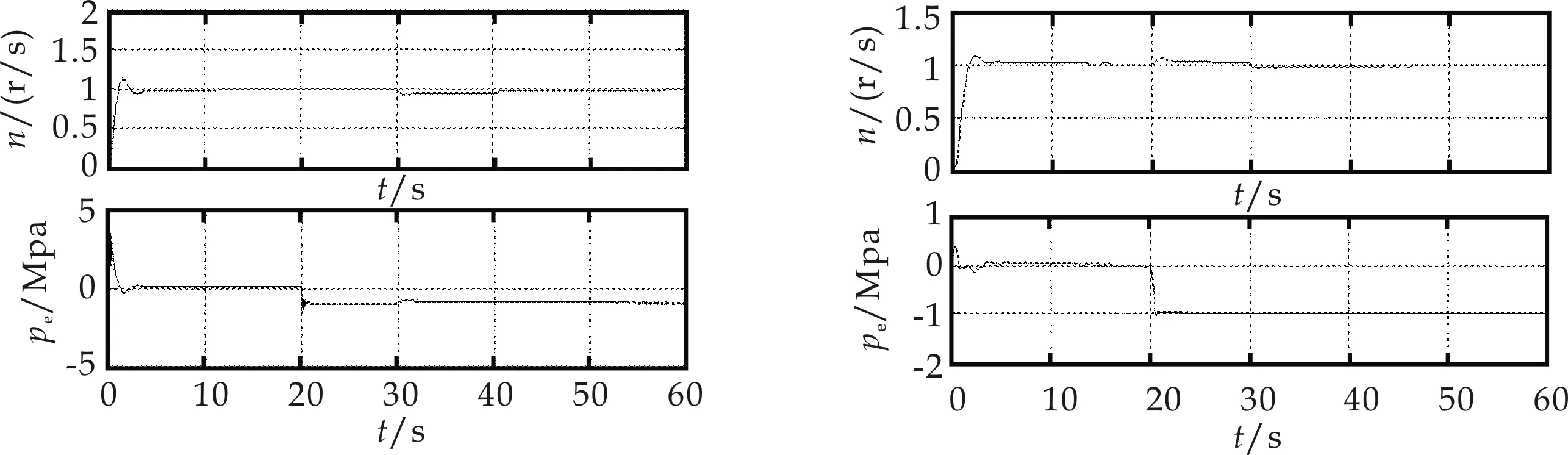
(c)加入電負荷擾 (d)加入電負荷擾圖11 解耦控制系統性能測試響應曲線

圖11中(a)、(b)分別為單抽汽輪機耦合系統中油動機1時間常數發生25%的變化時的對角解耦和模糊解耦控制仿真結果.由仿真結果可知：當油動機時間常數發生變化時，對角解耦控制系統對于電負荷的突變，其轉速響應曲線超調大，調節時間長，同時抽汽壓力回路的輸出有明顯的波動和超調.而采用模糊解耦控制時，系統響應速度加快，超調減小，仍然具有良好的魯棒性、跟蹤性，并能有效的實現系統解耦.

圖(11)(c)、(d)分別為在第30 s時加入100%的電負荷擾動后的對角解耦控制和模糊解耦控制響應曲線圖.從圖中可以看出第30 s時，對角解耦控制中抽汽壓力的響應曲線發生明顯的波動且過渡時間長.而采用模糊解耦時抽汽壓力響應曲線幾乎不受影響，系統具有更好的解耦效果及抗干擾能力.

5 結論

本文針對汽輪機系統存在強耦合及時變的特點，以解除熱電耦合以及提高控制系統對參數波動的適應性為目的，采用模糊控制器作為解耦器，設計了一種基于模糊解耦控制的單抽汽輪機控制系統.仿真結果表明本系統不僅具有較強的抗干擾能力、魯棒性，而且能有效地實現單抽汽輪機的熱電解耦控制，同時該控制系統對參數變化具有較好的適應性.

[1] 郭鈺峰,徐志強,于達仁.汽輪機調節原理[M].2版.北京:機械工業出版社,2010.

[2] 唐 麗.抽汽式汽輪機熱電牽連解耦控制的研究與應用[J].電站系統工程,2009,25(1):61-63.

[3] 史毅越.抽汽式汽輪機的模型辨識及熱電解耦[D].南京:東南大學,2014.

[4] 紀云鋒.抽汽汽輪機組DEH系統的解耦控制[J].液壓與氣動,2007(5):49-50.

[5] 裘潯雋,楊瑜文,林中達.用多變量模糊神經網絡實現雙抽汽輪機熱電負荷的解耦控制[J].汽輪機技術,2003,45(2):76-79.

[6] 吳優福,裘潯雋.用神經網絡實現雙抽汽輪機的負荷解耦控制及仿真[J].能源研究與利用,2003(1):29-32，40.

[7] 陳 蓓,田 娜,姚 培.基于單神經元自適應PID的水分定量內模解耦控制[J].陜西科技大學學報(自然科學版),2008,26(3):91-95.

[8] 高希明,孟彥京.一種基于神經元的解耦控制算法研究[J].陜西科技大學學報(自然科學版),2009,27(1):110-113.

[9] 胡 燦,田小梅.基于耦合度分析的家禽孵化過程模糊解耦控制系統[J].衡陽師范學院學報,2016,37(3):26-29.

[10] 麥雪鳳,寧甲宇.焦爐集氣管壓力模糊解耦及吸力協調控制與應用[J].冶金自動化,2015,39(1):72-76.

[11] 王 茹,陶澤炎.基于模糊前饋解耦的變風量空調控制方法研究[J].計算機測量與控制,2015,23(2):450-453，456.

[12] 王昕煜,趙靜一,徐麗杰.橋梁同步頂升模糊解耦控制策略研究[J].中國工程機械學報,2015,13(4):347-352，371.

[13] 王江鵬.基于模糊解耦的精餾塔溫度控制的仿真研究[D].昆明：昆明理工大學,2015.

[14] 張 玲,張文苑,鄭恩讓.一種模糊解耦控制系統的設計與仿真研究[J].計算機仿真,2010,27(8):118-121.

[15] 柴天佑.多變量自適應解耦控制及應用[M].北京：科學出版社，2001.

【責任編輯：陳 佳】

Fuzzy decoupling control of thermo-electric coupling single extraction turbine

LI Yan1,2， TUO Fu-ting1， LIU Li-fang3

(1.College of Electrical and Information Engineering, Shaanxi University of Science & Technology, Xi′an 710021, China; 2.Shaanxi Research Institute of Agricultural Products Processing Technology, Xi′an 710021, China; 3.College of Vocational Normal Education, Shaanxi University of Science & Technology, Xi′an 710021， China)

Parameter uncertainty and serious coupling relationship exists between heat load and electric load are two major problem in extraction steam turbine,a small change in either load of the two will cause further fluctuations,thereby affecting the performance of the turbine control system.To solve these problems,taking a 6 MW single extraction steam turbine from power plant of a paper mill as a case.Based on the analysis of its working principle we establish a mathematical model.Then,we analysis its strong coupling characteristics,and design a fuzzy decoupling control method to achieve decoupling and improve the thermoelectric system adaptability,according to the actual need .Finally,the Matlab / Simulink simulation results show that,compared to conventional diagonal decoupling,the method in strong coupling model parameters and there are some fluctuations,it can still ensure better stability and robustness.

turbine； thermoelectric load coupling； mathematical model； fuzzy decoupling control

2016-11-27

陜西省科技廳科學技術研究發展計劃項目(2013K07-28)； 陜西省教育廳專項科研計劃項目(14JK1094)

李 艷(1972-)，女，四川仁壽人，副教授，碩士，研究方向：工業自動化、智能檢測與智能控制

2096-398X(2017)03-0159-07

TK261

A