一類位置不變重尾指數估計
李彤彤
(山西大學 數學科學學院, 山西 太原 030006)
?
一類位置不變重尾指數估計
李彤彤
(山西大學 數學科學學院, 山西 太原 030006)
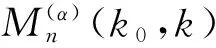
重尾分布; 極值指數; 位置不變; 正規變化; 均方誤差; 漸近性質; Hill估計
0 引言
重尾分布普遍存在于社會的各個領域中,例如:生物統計學、金融學、保險和風險理論等.為了了解尾部的相關信息和規律性,對重尾指數 的估計變得尤為重要,并且重尾極值指數估計的有效性、穩健性已經備受人們的關注.Pickands估計、Hill估計、矩估計和核估計是最經典的、最基礎的極值指數估計,當γ>0時,最為著名的是Hill估計量[1]:
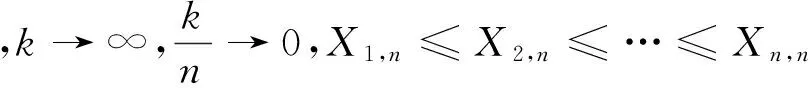
對于更為廣泛的情況γ∈R,Dekkers,Einmahl和de Haan[7](1989)提出了矩估計:
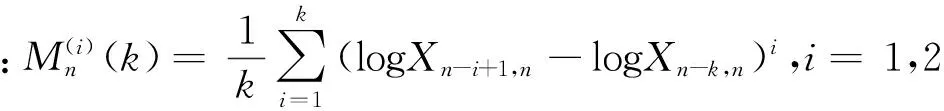
Ling等[8,9]在2007年在矩估計的基礎上,提出了一類位置不變的矩估計量.鄒佶叡等[10]在2006年提出了漸近無偏矩估計量.
然而,Hill估計和矩估計雖然有許多優點,但它們對門限k0的值較為敏感,換句話說,上述的這些估計都不滿足位置不變性,Pickands(1975)[11]在假定尾部分布函數的前提下,通過求分位數給出了一類位置不變估計:
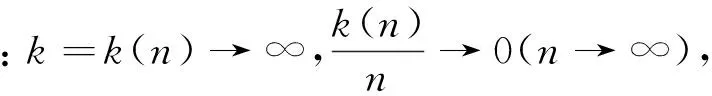
其中:k=k(n)=o(n),k0=o(k(n)),k(n)→∞,k0→∞(n→∞).Li等[13,14]也提出了一類位置不變的Hill估計,隨后劉維奇等[15]進一步闡明了重尾指數估計的研究進展,陶寶[16]討論了另一類Hill型位置不變的估計量的強相合性,而Ling[17]還提出了Weiss類Hill估計.
在許多學者研究位置不變性的同時,降偏差的研究也越來越受到人們的重視,deHaanL等[5],Beirlant等[18]、Feuerverger等[19],Caeiro等[20],Gomes等[21]對Hill估計進行了改進,降低了漸近偏差,BrahimB等[22]的降偏差估計,以此作為基礎,劉維奇等[23]利用降偏差的方法對Caeiro等人提出的改進Hill估計及Gomes等人的估計進行了重新修正.
1.1 正則變化條件
為了研究重尾極值指數相關的漸近性質,下面給出二階正則變化條件:
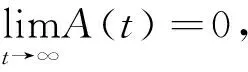
(1)
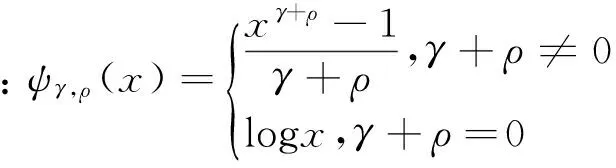
且有|A(t)|∈RVρ(ρ≤0)[deHaanL,Ferreira[24]中推論2.3.5]
(2)存在可測函數A(t)>0且A(t)→0(t→∞),使得
(2)
對一切x>1,y>1局部一致成立,其中:
(3)
且對上述條件有二階參數ρ<0及|A(t)|∈RVρ.
FrageAlves[12]提出位置不變的Hill估計:
Ling等[8,9]提出的位置不變矩估計:
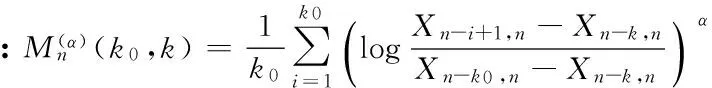
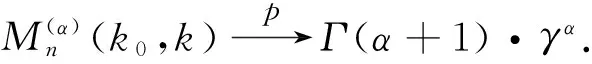
鑒于此,本文提出一類新的位置不變的重尾極值指數估計量:
(α∈R+)
為方便計算,本文需要規定以下記號以及變量:
引理1 當γ>0,ρ<0時,若1.1中公式(1)成立,則對任意的ε,δ>0存在t0=t0(ε,δ),使得對一切t>t0及x>1時
(4)
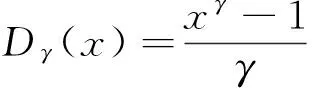
引理2 在引理1的條件下,對一切x>1,y>1有
(5)
此外,對任意的ε,δ>0,存在t0=t0(ε,δ)使得t>t0時
Tγ,ρ(x,y)
對于x>y>1局部一致成立,其中
Fγ,ρ(x,y)=

(6)
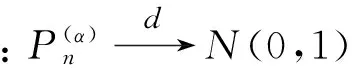
(7)
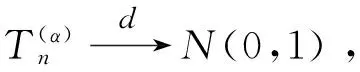
(8)

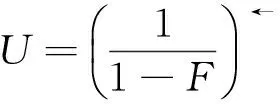
成立.
若γ+ρ≠0,由引理3可得:
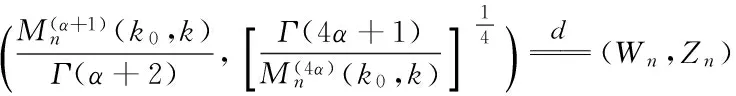
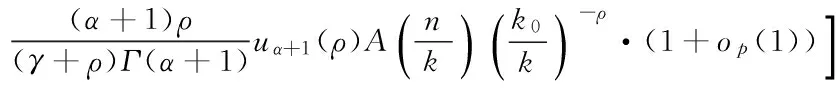
令
它的特征函數為:
fk0(t)=
從而
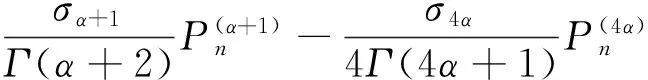
同理可證γ+ρ=0的情形.
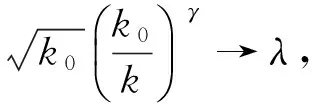
1.3k0的最優選擇
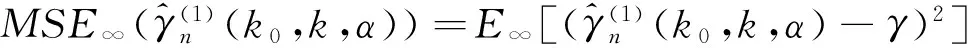
定理2 設A(t)~ctρ,其中ρ<0,c≠0,若1.1節中二階正規條件公式(1)成立.記
則有如下結論:
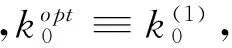
2.當γ>-ρ時,
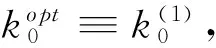
(2)若k?n,則
(3)若k~Dn,D≠0,則有
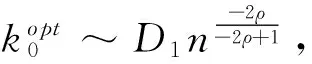
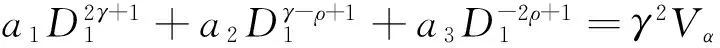
證明:設A(t)~ctρ,c≠0分以下情況討論:
(1)若γ<-ρ時,其漸近展開式為
(9)
且
要使MSE最小,對k0求偏導,可得:
(10)
(2)若γ>-ρ時
從而可得
(11)
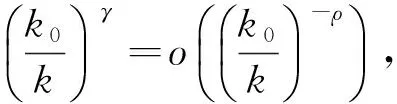
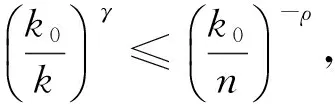
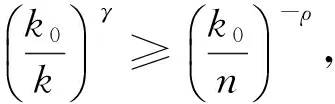
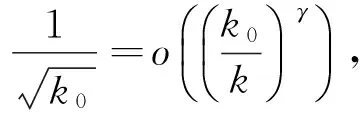
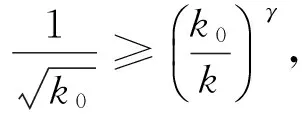
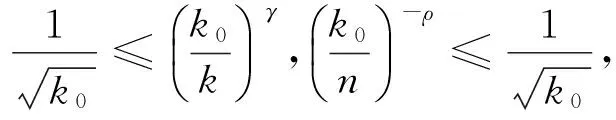
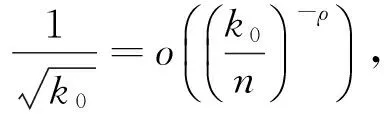
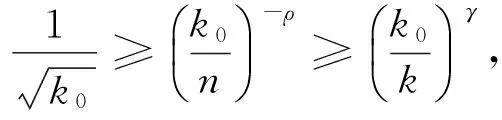
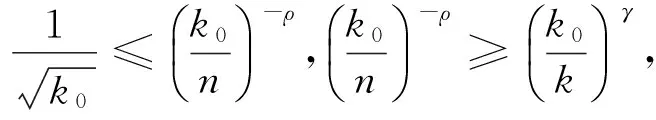
則n≤k0≤k·n
上述幾種情況,與(10)證明類似,可求出k0的最優解.

推論3 在推論2的基礎上
令
則
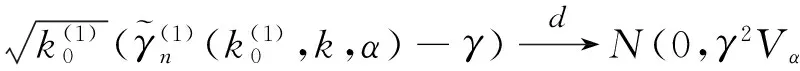
2 模擬與比較
對于同一個極值指數,通常采用經驗似然,極大似然等模擬方法,通過討論估計量的相對漸近效、均值和均方誤差等實現對其的評價.
2.1 參數α的選取
(12)
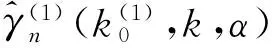
2.2 兩類位置不變估計的模擬比較
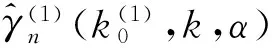
(1)Pareto(γ)分布
F(x)=1-x,(x>0,γ>0)
(2)Frechet(γ)分布
(3)Burr(α,β)分布
F(x)=1-(1+xα)-β,(x≥0,α,β>0)
(a)均值 (b)均方誤差圖1 極值指數γ=0.5的Pareto分布,估計量與的模擬均值(a)和均方誤差(b)
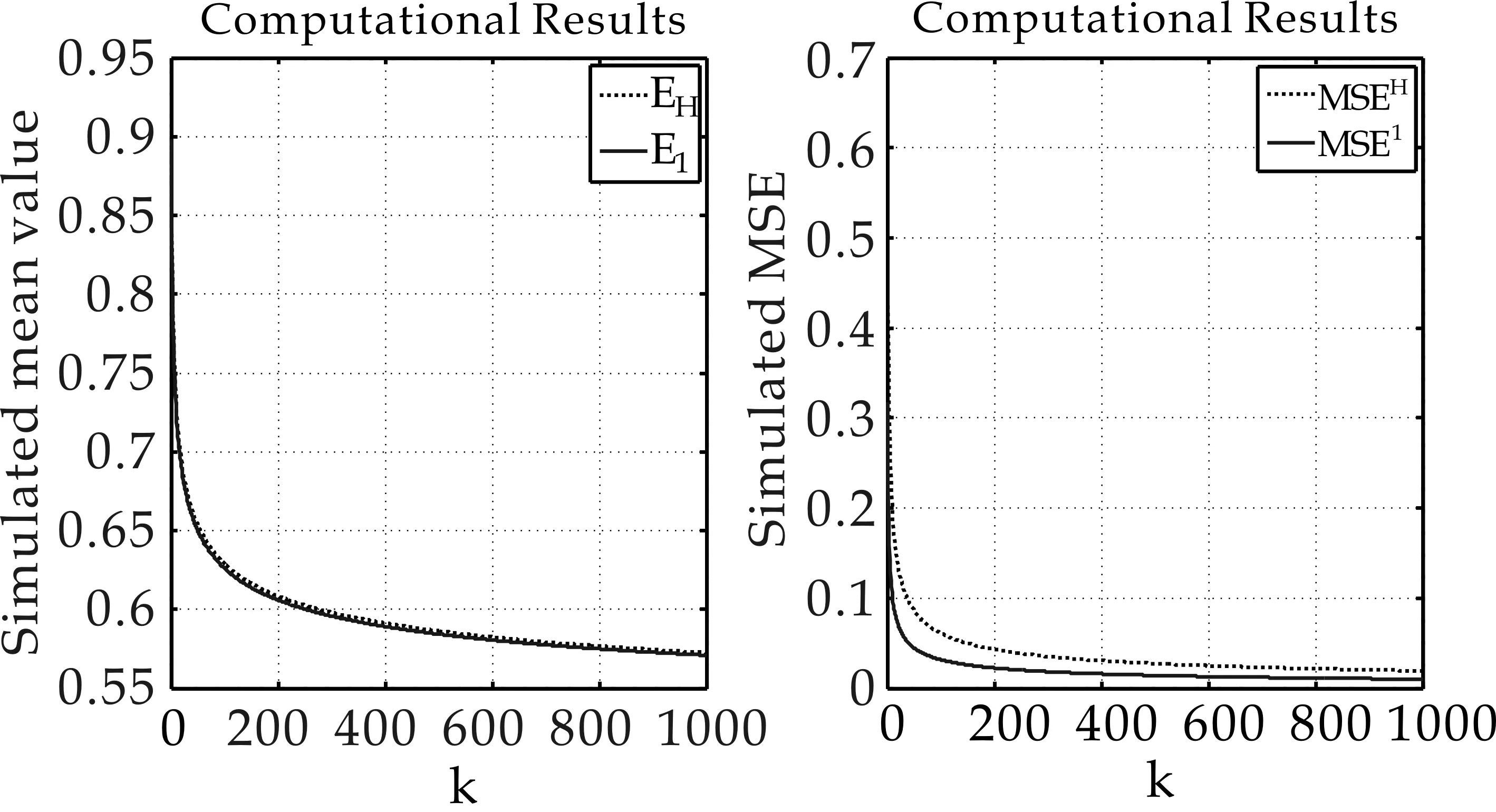
(a)均值 (b)均方誤差圖2 極值指數γ=1的Frechet分布,估計量與的模擬均值(a)和均方誤差(b)
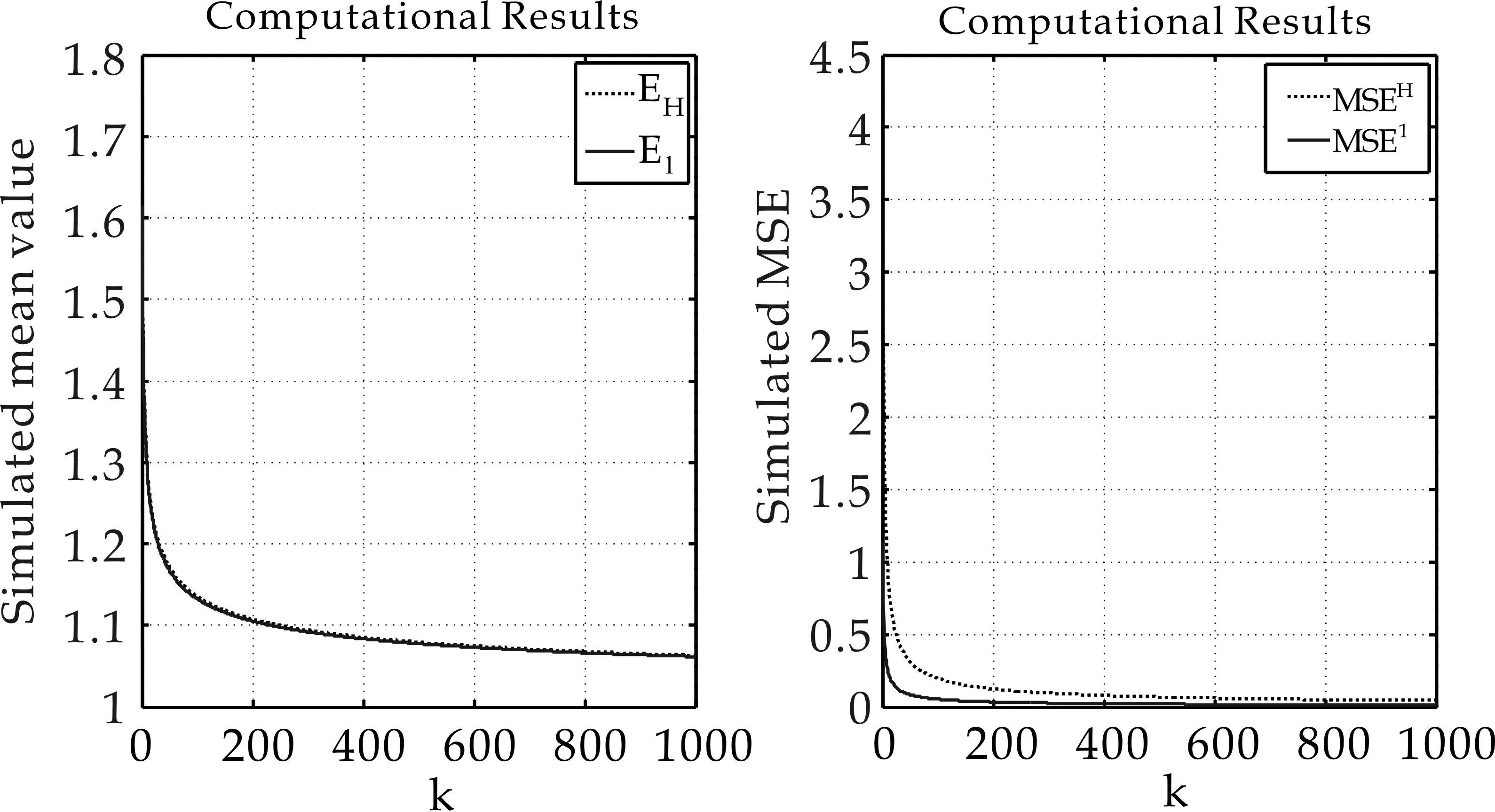
(a)均值 (b)均方誤差圖3 極值指數γ=2的Burr分布,估計量與的模擬均值(a)和均方誤差(b)
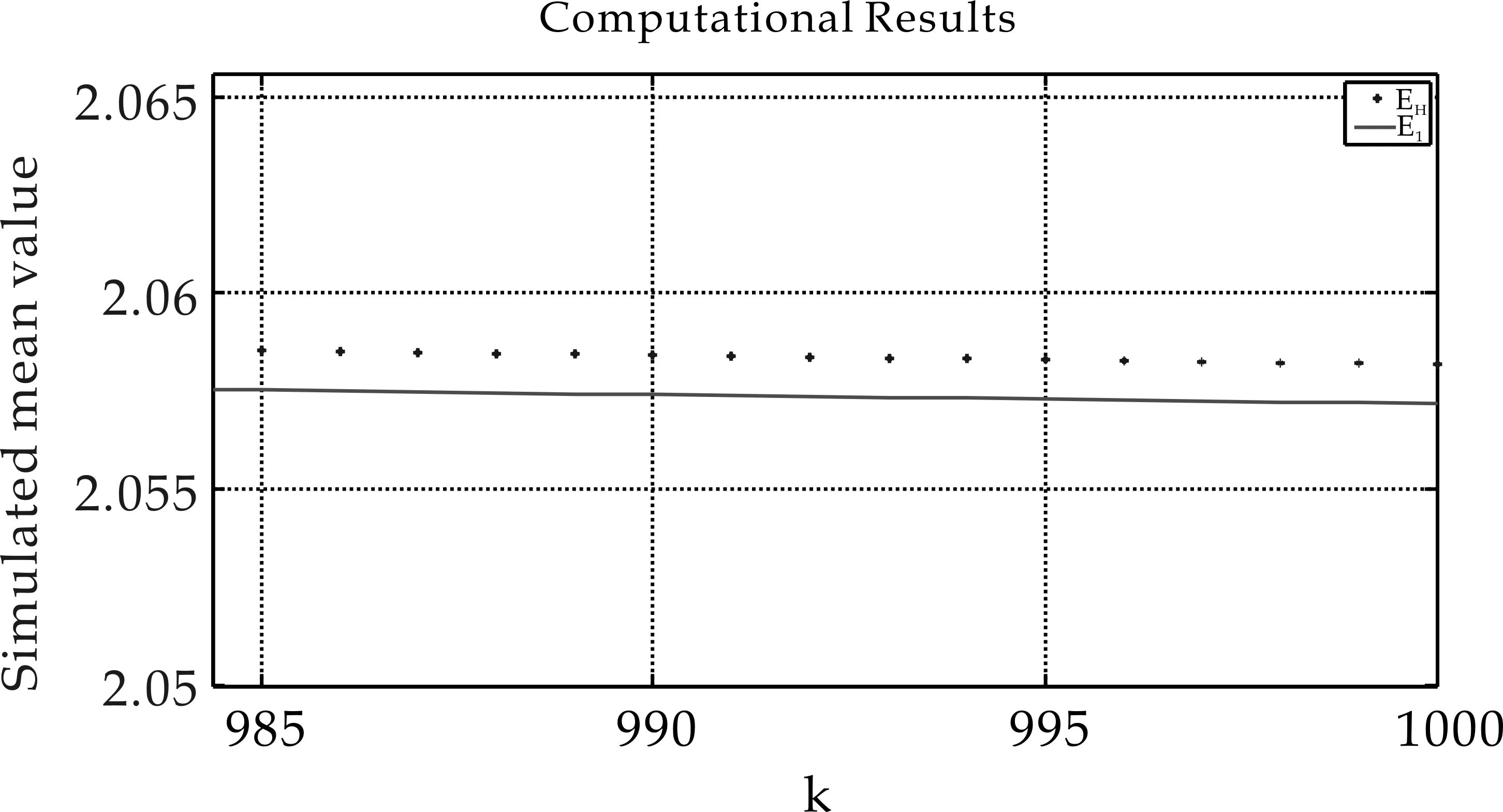
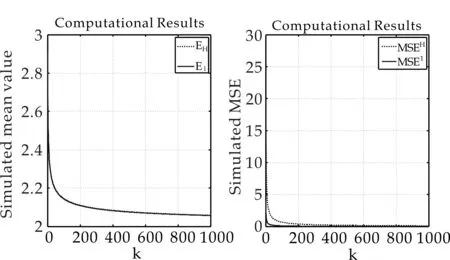
圖4 極值指數γ=2的Burr分布,估計量與模擬均值的部分放大截圖
3 結論
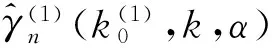
[1]HillBM.Asimplegeneralapproachtoinferenceaboutthetailofadistribution[J].AnnStatist,1975,3(5):1 163-1 174.
[2] 彭 亮,祁永成.二階正規變化子模型下Hill型估計量漸進正態性[J].數學年刊,1997,18(5):539-544.
[3]GomesMI,MartinsMJ.GeneralizationsoftheHillestimator-asymptoticversusfinitesamplebehaviour[J].StatPlanInference, 2001,93(1-2):161-180.
[4] 彭作祥.一類Hill型估計量的收斂性[J].西南師范大學學報,1998,23(2):133-137.
[5]deHaanL,PengL.Comparisonoftailindexestimators[J].StatisticsNeerlandica,1998,52(1):60-70.
[6]CaeiroF,GomesMI.Aclassofasymptoticallyunbiasedsemi-parametricestimatorofthetailindex[J].SociedaddeEstadisticaeInvestigationOperativeTest,2002,11(2):345-364.
[7]DekkersA,EinmahlJ,deHaanL.Amomentestimatorfortheindexofanextremevaluedistribution[J].AnnalsofStatistics,1989,17(4):1 833-1 855.
[8]LingC,PengZ,NadarajahS.Alocationinvariantmoment-typeestimatorI[J].TheoryofProbabilityandMathematicalStatisics, 2008,76:23-31.
[9]LingC,PengZ,NadarajahS.Alocationinvariantmoment-typeestimatorII[J].TheoryofProbabilityandMathematicalStatisics,2008,77:177-189.
[10] 鄒佶叡,凌成秀.漸進無偏矩估計量[J].西南師范大學學報(自然科學版),2006,31(3):19-23.
[11]PickandsJ.Statisticalinferenceusingextremeorderstatistics[J].AnnalofStatistics,1975,3(1):119-131.
[12]FragaAlvesMI.AlocationinvariantHill-typeestimator[J].AnnalofStatistics,2001,4(3):199-217.
[13]LiJ,PengZ,NadarajahS.AclassofunbiasedlocationinvariantHill-typeestimatorsforheavytaileddistributions[J].ElectronicJournalofStatistics,2008,2(3):829-847.
[14]LiJ,PengZ,NadarajahS.Asymptoticnormalityoflocationinvariantheavytailindexestimators[J].Extremes,2010,13(3):269-290.
[15] 劉維奇,邢紅衛.重尾分布尾指數估計研究進展[J].山西大學學報(自然科學版),2012,35(2):163-173.
[16] 陶 寶.位置不變的Hill型估計量的強相合性[J].重慶工商大學學報(自然科學版),2006,23(4):331-333.
[17]LingC,PengZ,NadarajahS.Locationinvariantweiss-Hillestimator[J].Extremes,2012,15(2):197-230.
[18]BeirlantJ,DierckxG,GoegebeurY,etal.Tailindexestimationandanexponentialregressionmodel[J].Extremes,1999,2(2):177-200.
[19]FeuervergerA,HallP.Estimatingatailexponentbymodelingdeparturefromaparetodistribution[J].AnnalsofStatistics,1999,27(2):760-781.
[20]GaeiroF,GomesMI,PestanaD.DirectreductionofbiasoftheclassicalHillestimator[J].Revstat,2005, 3(2):113-136.
[21]GomesMI,MartinsMJ,NevesMM.Improvingsecondorderreduced-biastailindexestimation[J].Revstat, 2007,5(2):177-207.
[22]BrahimB,DjamelM,AbdelhakimN,etal.Abias-reducedestimatorforthemeanofaheavy-taileddistributionwithaninfinitesecondmoment[J].JournalofStatisticalPlanningandInference,2013,143(6):1 064-1 081.
[23] 劉維奇,邢紅衛.重尾指數估計中閾值k的簡單優化估計[J].系統工程理論與實踐,2010,30(8):1 465-1 470.
[24]deHaanL,FerreiraA.Extremevaluetheoryanintroduction[M].NewYork:SpringerScienceUsinessMedia,2006.
【責任編輯:蔣亞儒】
A class of heavy tailed index estimator of location invariant
LI Tong-tong
(School of Mathematical Sciences, Shanxi University, Taiyuan 030006, China)
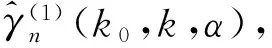
heavy tailed distribution; extreme value index; location invariant; regular variation; mean square error; asymptotic properties; Hill estimate
2017-02-13
教育部人文社會科學研究項目(14YJA790034)
李彤彤(1989-),男,山西太原人,在讀碩士研究生,研究方向:時間序列分析
2096-398X(2017)03-0180-06
O212.4
A

