潛在特質(zhì)模型在疾病易感性評(píng)價(jià)中的應(yīng)用*

劉 娜 石志紅 曹紅艷 郭興萍 張巖波△

潛在特質(zhì)模型在疾病易感性評(píng)價(jià)中的應(yīng)用*

劉 娜1石志紅1曹紅艷1郭興萍2△張巖波1△

目的 介紹潛在特質(zhì)模型的原理、方法和技術(shù)，探討潛在特質(zhì)模型在疾病易感性評(píng)價(jià)中的應(yīng)用。方法 以出生缺陷數(shù)據(jù)為實(shí)例，采用R 2.5.1軟件的Ltm包例證潛在特質(zhì)模型的構(gòu)建和分析原理。結(jié)果 通過對(duì)出生缺陷數(shù)據(jù)進(jìn)行潛在特質(zhì)模型擬合，潛在特質(zhì)得分能夠很好地預(yù)測(cè)評(píng)估其發(fā)病危險(xiǎn)。結(jié)論 潛在特質(zhì)模型用于疾病患病風(fēng)險(xiǎn)評(píng)價(jià)有很好的效果。

潛在特質(zhì)模型 疾病易感性評(píng)價(jià) 出生缺陷 潛在特質(zhì)得分

潛變量模型(latent variable model)利用外在直接觀察到的變量分析內(nèi)在因素，通過分析外在變量與內(nèi)在變量(潛變量)及內(nèi)在變量之間的關(guān)系來探究事物的發(fā)生、發(fā)展、變化規(guī)律及特點(diǎn)[1]。潛在特質(zhì)模型(latent trait model)屬于潛在變量模型的一種，兼具因子分析與聚類分析的功能，具有數(shù)據(jù)降維、數(shù)據(jù)挖掘和理論驗(yàn)證的統(tǒng)計(jì)學(xué)功能，適用于顯變量為分類型，潛變量為連續(xù)型的資料[2]。在醫(yī)學(xué)研究中，對(duì)疾病易感性的評(píng)價(jià)涉及影響因素非常多，既有能夠較為準(zhǔn)確測(cè)量的因素，又存在許多無法直接測(cè)量的指標(biāo)，同時(shí)，各指標(biāo)間可能存在相關(guān)。對(duì)這些因素的研究，不僅要研究單個(gè)變量的效應(yīng)，也要研究一組變量的整體效應(yīng)。傳統(tǒng)的患病風(fēng)險(xiǎn)評(píng)價(jià)，直接對(duì)暴露因素得分進(jìn)行簡(jiǎn)單相加求和以考察疾病危險(xiǎn)程度，并采用卡方檢驗(yàn)和logistic回歸進(jìn)行分析，顯然遠(yuǎn)不足以挖掘疾病的潛在暴露因素，無法綜合地評(píng)價(jià)疾病的患病風(fēng)險(xiǎn)。因此，本文將介紹潛在特質(zhì)模型在疾病患病風(fēng)險(xiǎn)評(píng)價(jià)中的應(yīng)用，為易感性評(píng)價(jià)提供良好的分析策略。

方法與原理

1.模型結(jié)構(gòu)

潛在特質(zhì)模型包括兩個(gè)部分：第一部分是測(cè)量模型，反映了顯變量與潛變量之間的關(guān)系，可以解釋各顯變量之間的潛在結(jié)構(gòu)；第二部分是結(jié)構(gòu)模型，研究潛變量之間的結(jié)構(gòu)關(guān)系。

(1)測(cè)量模型

假定條目yj是分類變量，它有Lj個(gè)可能分類水平：l=1,…,Lj，不同類型的條目，分類變量水平是不同的。對(duì)于等級(jí)資料的條目，其分類變量水平是等級(jí)的，順序不能發(fā)生改變，除非采用反向記分；對(duì)于無序分類資料，其分類變量水平是隨機(jī)的；而對(duì)于二分類資料，既可以看成是等級(jí)資料也可以看成是無序分類資料。yi的測(cè)量模型其實(shí)是一個(gè)分類概率回歸模型：

πjl(η)=p(yj=l|η)

其中，η為解釋變量。

(2)結(jié)構(gòu)模型

潛在特質(zhì)模型假定潛在變量η取某一固定值時(shí)，j維列聯(lián)表x可通過其邊際分布來解釋，在此假設(shè)條件下，潛在因子分布pη為結(jié)構(gòu)模型。一般情況下，假設(shè)潛在因子η服從均數(shù)為k，標(biāo)準(zhǔn)差為φ的正態(tài)分布，即η～N(k,φ)。在模型設(shè)定中，一般限定k=0，φ=1，否則需調(diào)整測(cè)量模型中的參數(shù)。

2.常見的潛在特質(zhì)模型

潛在特質(zhì)模型在心理測(cè)量領(lǐng)域被稱為項(xiàng)目反應(yīng)理論，它建立了組成測(cè)驗(yàn)的項(xiàng)目與測(cè)驗(yàn)分?jǐn)?shù)之間的函數(shù)關(guān)系。到目前為止，潛在特質(zhì)模型產(chǎn)生了至少20余種模型。可以根據(jù)不同的反應(yīng)數(shù)據(jù)選擇相應(yīng)的模型來估計(jì)參數(shù)。

(1)Rasch模型

Rasch模型在1960年首次被Rasch提出，是一個(gè)單維潛在特質(zhì)模型的特例，它的區(qū)分度是相同的，主要應(yīng)用于教育測(cè)驗(yàn)，目的是研究特定個(gè)體的能力值，可以用潛在因子對(duì)量表內(nèi)的項(xiàng)目進(jìn)行評(píng)估[4]。模型被定義為：

其中，P(Yij=1)代表第i個(gè)個(gè)體對(duì)第j個(gè)條目正確回答的概率。θ表示能力值，β表示難度系數(shù)[5]。

(2)雙參數(shù)logistic模型(Ltm模型)

對(duì)于顯變量為二分類的數(shù)據(jù)，潛在特質(zhì)模型與因子分析模型相似，是潛在特質(zhì)模型的一種。模型假設(shè)有相互依賴關(guān)系的外顯變量可以被少數(shù)的幾個(gè)潛變量所解釋。該模型的公式是項(xiàng)目反應(yīng)理論框架下的一種方法。

其中，α代表區(qū)分度系數(shù)。

3.參數(shù)估計(jì)方法

潛在特質(zhì)模型的參數(shù)估計(jì)一般采用極大似然法(maximumlikelihoodestimators)[3]，其迭代過程常用的算法有EM算法和擬牛頓法(quasi-Newton)。本文參數(shù)估計(jì)選用混合算法進(jìn)行計(jì)算，即開始時(shí)使用EM算法進(jìn)行迭代，然后用擬牛頓算法迭代直至收斂。

4.模型評(píng)價(jià)

潛在特質(zhì)模型常用的評(píng)價(jià)方法有似然比檢驗(yàn)、Pearson檢驗(yàn)及AIC(akaikeinformationcriterion)指標(biāo)和BIC(bayesianinformationcriterion)指標(biāo)。AIC和BIC的值越小，模型擬合越好[6-8]。本文綜合使用AIC、BIC及似然比檢驗(yàn)進(jìn)行模型擬合優(yōu)劣比較。同時(shí)，采用雙變量邊際殘差進(jìn)一步地判斷模型擬合是否良好。

5.潛在特質(zhì)得分與主成分得分

最優(yōu)模型確定后，將觀察值代入模型中，獲得個(gè)體潛在特質(zhì)的預(yù)測(cè)值，即給出各條目綜合得分。其條件均數(shù)為：

同時(shí)，計(jì)算出外顯變量對(duì)公共因子貢獻(xiàn)的權(quán)重αi1，即得出該模型的主成分得分：

C1(y)=∑αi1yi

潛在特質(zhì)得分與主成分得分對(duì)不同條目進(jìn)行了聚類，挖掘了其隱含的內(nèi)在信息，綜合反映了各條目之間的整體效應(yīng)，實(shí)現(xiàn)了降維的目的，可以作為衡量疾病易感性的重要指標(biāo)，得分越高，患病的危險(xiǎn)性越大。

實(shí)例分析

為實(shí)證潛在特質(zhì)模型應(yīng)用原理，本文利用2006-2008年在山西省6個(gè)出生缺陷高發(fā)縣(市)收集的有效問卷36712份進(jìn)行潛在特質(zhì)模型分析。問卷內(nèi)容包括七個(gè)方面：調(diào)查兒母親一般情況、母親既往病史、妊娠早期營(yíng)養(yǎng)狀況、妊娠早期患病、妊娠早期服藥、妊娠早期周邊環(huán)境、妊娠早期生活習(xí)慣，共計(jì)25個(gè)條目。將所有條目轉(zhuǎn)化為二分類變量，如母親年齡大于等于35歲的為1，小于35歲的為0。本文僅對(duì)調(diào)查兒母親一般情況和妊娠早期患病這兩個(gè)維度進(jìn)行潛在特質(zhì)分析。采用R 2.5.1軟件的Ltm包進(jìn)行分析。

結(jié) 果

對(duì)調(diào)查兒母親一般情況和妊娠早期患病這兩個(gè)維度進(jìn)行模型擬合，得到參數(shù)估計(jì)結(jié)果，結(jié)合AIC、BIC和似然比檢驗(yàn)對(duì)Ltm模型與Rasch模型進(jìn)行擬合優(yōu)度評(píng)價(jià)，選出最優(yōu)模型。此外還可用雙變量邊際殘差的方法對(duì)模型進(jìn)行評(píng)估。最后通過計(jì)算潛在特質(zhì)得分及主成分得分，對(duì)出生缺陷患病風(fēng)險(xiǎn)進(jìn)行評(píng)價(jià)。

1.參數(shù)估計(jì)結(jié)果

本文采用最大似然估計(jì)算法得到雙參數(shù)的值，其中α代表區(qū)分度系數(shù)，β代表難度系數(shù)。由表1可知各條目的區(qū)分度系數(shù)為0.2819～7.6206，總的來講能很好的反映不同受試者的能力。β值在1.6486～7.8763，本文中我們暫不對(duì)其難度系數(shù)進(jìn)行考慮。具體參數(shù)估計(jì)結(jié)果見表1。

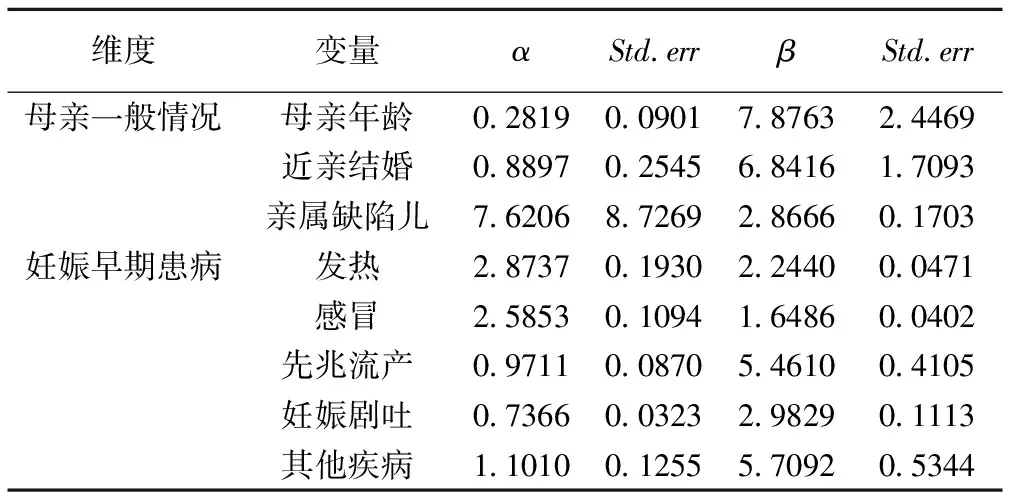
表1 出生缺陷母親一般情況及妊娠早期患病參數(shù)估計(jì)結(jié)果

2.模型適配結(jié)果及擬合優(yōu)度評(píng)價(jià)

對(duì)出生缺陷數(shù)據(jù)進(jìn)行Ltm與Rasch模型擬合，其中，母親一般情況及妊娠早期患病兩個(gè)維度擬合Ltm與Rasch模型結(jié)果見表2。

由表2可知，Ltm模型的AIC和BIC值比Rasch模型所得值小，AIC和BIC值越小，模型擬合越好。似然比檢驗(yàn)顯示，兩個(gè)模型檢驗(yàn)都有統(tǒng)計(jì)學(xué)意義。Ltm模型比Rasch模型能更好的擬合出生缺陷數(shù)據(jù)。同時(shí)雙變量邊際殘差結(jié)果也顯示模型擬合效果良好。

表2 母親一般情況及妊娠早期患病Ltm與Rasch模型擬合結(jié)果

3.潛在特質(zhì)得分與主成分得分

將出生缺陷相關(guān)暴露因素放入Ltm模型進(jìn)行擬合，可以得到多個(gè)反應(yīng)模式。為了便于比較，將每個(gè)暴露因素為“是”的賦值為1，為“否”的賦值為0，直接相加求和得分，定義為“表面得分”。母親一般情況和妊娠早期患病兩個(gè)維度的表面得分與潛在特質(zhì)得分結(jié)果見表3。

表3中，不同反應(yīng)模式下，潛在特質(zhì)得分為-0.029～3.009，即隨著暴露因素的增多，潛在特質(zhì)得分增大，出生缺陷發(fā)生的危險(xiǎn)性變大。另一方面，通過對(duì)不同反應(yīng)模式的比較，如(0 0 1)和(0 1 0)可知各主成分得分是不一樣的。顯然，在母親一般情況維度，親屬有缺陷兒的孕母發(fā)生出生缺陷的風(fēng)險(xiǎn)更大。同理，表4結(jié)果提示單因子暴露下，發(fā)熱與感冒發(fā)生出生缺陷的風(fēng)險(xiǎn)較大，不同暴露組合發(fā)病風(fēng)險(xiǎn)可由潛在特質(zhì)得分評(píng)價(jià)。

進(jìn)一步將出生缺陷組的潛在特質(zhì)得分與非出生缺陷組的潛在特質(zhì)得分做t檢驗(yàn)，所得結(jié)果見表5。

表3 母親一般情況潛在特質(zhì)得分

表4 妊娠早期患病情況潛在特質(zhì)得分

表5 出生缺陷組和非出生缺陷組在母親一般情況與妊娠早期患病兩個(gè)維度中的潛在特質(zhì)得分比較

由表5可知，兩個(gè)維度出生缺陷組和非出生缺陷組的潛在特質(zhì)得分差異有統(tǒng)計(jì)學(xué)意義，認(rèn)為出生缺陷組的潛在特質(zhì)得分明顯高于非出生缺陷組。

討 論

潛在特質(zhì)模型是潛變量分析的一種，是探討外顯變量為分類變量，潛變量為連續(xù)變量的一種最佳統(tǒng)計(jì)方法。通過潛在特質(zhì)變量解釋多個(gè)外顯變量間的復(fù)雜關(guān)系，并將其外顯變量綜合為一個(gè)潛變量，使之能夠代替外顯變量分析整體效應(yīng)。通過所得到的潛在特質(zhì)得分的大小可以對(duì)疾病患病風(fēng)險(xiǎn)進(jìn)行評(píng)價(jià)。實(shí)例分析中的外顯變量為二分類變量，但在實(shí)際應(yīng)用中潛在特質(zhì)模型還可應(yīng)用于多分類的名義變量、有序變量等[9]。

目前，潛在特質(zhì)模型分析的軟件很多，如R、Mplus、Multilog等。本文運(yùn)用R軟件中的Ltm包進(jìn)行分析，相對(duì)于其他軟件，不僅能夠得到潛在特質(zhì)得分，而且具有語(yǔ)法結(jié)構(gòu)簡(jiǎn)單，易于掌握的特點(diǎn)和優(yōu)勢(shì)。

本文分析母親一般情況和妊娠早期患病兩個(gè)維度，采用的是雙參數(shù)logistic模型(Ltm模型)。不同反應(yīng)模式下，潛在特質(zhì)得分不同。暴露因素越少，得分越低，反之，得分越高。同時(shí)根據(jù)不同反應(yīng)模式的主成分得分不同，對(duì)各維度暴露因素權(quán)重進(jìn)行了比較。可進(jìn)一步探索多因子潛在特質(zhì)模型，將暴露因素綜合為幾個(gè)潛在因子，并對(duì)其關(guān)聯(lián)性進(jìn)行分析；也可采用多樣本潛在特質(zhì)模型，對(duì)不同樣本的暴露因素進(jìn)行比較，進(jìn)一步挖掘出疾病暴露因素，提高疾病預(yù)測(cè)精度。

[1]張巖波.潛變量分析.北京:高等教育出版社,2009:220-246.

[2]Moustaki I,Knott M.Generalized latent trait models.Psychometrika,2000,65(3):391-411.

[3]David J.Latent Variable Models and Factor Analysis:A Unified Approach,3rd;Edition.International Statistical Review,2013,81(2):333-334.

[4]晏子.心理科學(xué)領(lǐng)域內(nèi)的客觀測(cè)量—Rasch 模型之特點(diǎn)及發(fā)展趨勢(shì).心理科學(xué)進(jìn)展,2010,18(08):1298-1305.

[5]Yu-Feng Huang,Mei-Yung Tsou,En-Tzu Chen,et al.Item response analysis on an examination in anesthesiology for medical students in Taiwan:A comparison of one-and two-parameter logistic models.Journal of the Chinese Medical Association,2013,76(6):344-349.

[6]Gollini I,Murphy TB.Mixture of latent trait analyzers for model-based clustering of categorical data.Statistic & Computing,2013,24(4):569-588.

[7]Choi I.Model Selection for Factor Analysis:Some New Criteria and Performance Comparisons.Working Papers,2013.

[8]Hirose K,Kawano S,Konishi S,et al.Bayesian Information Criterion and Selection of the Number of Factors in Factor Analysis Models.Journal of Data Science,2011,9.

[9]David Kaplan.The Sage Handbook of Quantitative Methodology for the Social Sciences.Applied Psychological Measurement,2006,30(5):447-451.

(責(zé)任編輯：劉 壯)

國(guó)家自然科學(xué)基金(71403156)

1.山西醫(yī)科大學(xué)公共衛(wèi)生學(xué)院衛(wèi)生統(tǒng)計(jì)學(xué)教研室(030001)

2.山西省計(jì)生委科研所

△通信作者：張巖波，E-mail：sxmuzyb@126.com;郭興萍，E-mail：13934527993@163.com