考慮循環取貨裝車堆碼的一種車輛路徑問題研究*

伊俊敏 蘇志雄

(廈門理工學院經濟與管理學院 廈門 361024)

考慮循環取貨裝車堆碼的一種車輛路徑問題研究*

伊俊敏 蘇志雄

(廈門理工學院經濟與管理學院 廈門 361024)

研究了某制造企業循環取貨物流路徑優化問題，根據弱異性小尺寸貨物裝車堆碼特點，在裝箱約束處理中通過“砌墻法”的有效簡化處理，得到車輛容積和裝車長度雙容量約束的新型車輛路徑問題模型，區別于已有帶裝箱約束的車輛路徑問題.將不同貨物作為單獨的節點來處理，解決了通常需要需求可拆分路徑問題才能解決的、節點需求量大于車輛容量的難題.運用遺傳算法求解，松弛雙容量的難約束，對該問題實際數據算例求得最終路徑-裝車結果.從結果解析、“砌墻”誤差分析、相關問題比較和應用條件等方面驗證了問題模型物流應用的可靠性和可行性.

車輛路徑問題；裝車堆碼；需求可拆分；遺傳算法；弱異性

0 引 言

循環取貨(milk-run)是汽車等制造企業應用的一種先進入廠物流模式，它是對不足整車運輸的多家供應商物料，按設計好的路線，采取多頻次、小批量的方式取貨，統一送到工廠生產現場的方式.通過對取貨順序、路線和頻次的總體安排來更好地控制入廠物流.循環取貨方式不僅降低了庫存，還加速了物流效率和線路合理性[1].

循環取貨優化的關鍵是路線設計和車輛裝車，這離不開帶容量限制的車輛路徑問題(CVRP)[2].但常規的CVRP模型并未考慮裝車，優化結果在實踐中卻裝不下[3].實際上，對這類需要拼裝貨物的配送問題，運輸和裝箱是2個相互制約、不可分割的過程，不考慮裝箱，車輛優化路線上的貨物卻無法全部裝上該車；忽視路徑問題，車廂裝得再滿成本也降不下來[4].因此，循環取貨物流的研究要綜合考慮路徑與車輛裝箱問題.

綜合考慮裝箱和路徑問題的最常見做法是將裝箱作為CVRP新的約束條件，來保證一條路線各節點的貨物能夠裝入車廂空間，并滿足不同客戶貨物的卸貨要求.當然具有裝箱約束的車輛路徑復合問題總的還是路徑成本最小的NP-難問題，但裝箱約束本身也是NP-難問題，兩者的復合更加難以求解.根據裝箱約束的維數，目前的研究分為二維問題(2L-CVRP)和三維問題(3L-CVRP)[5-9]，提升了車輛路徑問題和裝箱問題在物流運輸領域的實際應用并指明了方向.

另一方面，循環取貨作業常有將外地供應商的貨物先行集中到工廠附近取貨節點的操作，這些節點所需取貨量可能會超過車輛容量(稱為“大節點”)，已不滿足CVRP問題“節點惟一拜訪”的基本假設，需要考慮需求可拆分的車輛路徑問題(SDVRP)，允許該節點需求量被不同車輛分裝送貨.對于SDVRP問題，通過需求拆分可以形成更合理的路線來降低路徑問題的目標總里程[10].SDVRP雖然降低了總里程成本，但是對同一客戶的多次訪問卻提高了交易及管理成本，總的物流成本可能難以降低.從管理角度看，如果不是特別需要，并不值得推薦.

文中針對某物流循環取貨問題展開研究，通過簡化的裝車堆碼近似算法，得到專門的路徑-裝箱復合問題及模型.對實例數據，通過擴展節點的方法解決了“大節點”需求拆分的問題，運用遺傳算法求解，并給出結果及應用分析.

1 循環取貨裝車堆碼決策

針對汽車制造等行業生產需求的變化、眾多供應商和各零部件重量與尺寸的差異，Milk-run決策先要根據既定取貨周期下各零部件需要的數量，來綜合解決合理數量下取貨車輛的路線和裝箱的復合要求.

由于汽車零部件貨物體積尺寸差別大，無法全部托盤單元化，尤其是小尺寸零部件裝車常是包裝貨物在貨車車廂內堆碼的傳統方式.對于裝車堆碼，假設車型相同，即對任一車k(k=1,2,…,m)，載重量為Q，車廂內尺寸長、寬、高分別為L,W,H.每種貨物包裝的長寬高分別為li,wi,hi，其中裝車時hi不能倒置.

就裝箱優化來說，涉及到貨物裝車的三維容器裝箱問題，這類問題2種最基本的解法是砌墻法和分層法[11].對于本問題，弱異性小尺寸貨物，砌墻法更合適.

采用砌墻法可以近似算出每種貨物在車廂內同方向堆碼的墻厚ti(包裝箱長或寬的整數倍).這種近似算法設定每堵墻在車廂內垂直于車輛L方向，且橫貫整個車廂寬度(見圖1)，不考慮不同墻在車廂寬度方向的拼接.這時墻厚的計算公式如下.

(1)

2 路徑與裝箱復合問題的建模

解決了裝車堆碼之后，系統優化的關鍵問題是確定循環取貨路線安排和所需路線數量，以使總成本最小.這是CVRP類的路徑問題，首先是基本的模型假設[12]：

1) 每一車輛從倉庫出發并回到倉庫(回路問題)，中間每節點只拜訪一次.

2) 車輛到達一個節點后只取貨物，并且一次取完.

3) 所用車輛均相同，一條路線一輛車，每條路線所取貨物不超過車輛容量限制.

并采用以下記號：i為取貨節點，i=0,1,2,…,n，其中i=0表示倉庫;qi為每一取貨節點的取貨數量(以重量計)，i=1,2,…,n;cij為節點i和j之間的距離，i,j=0,1,2,…,n.

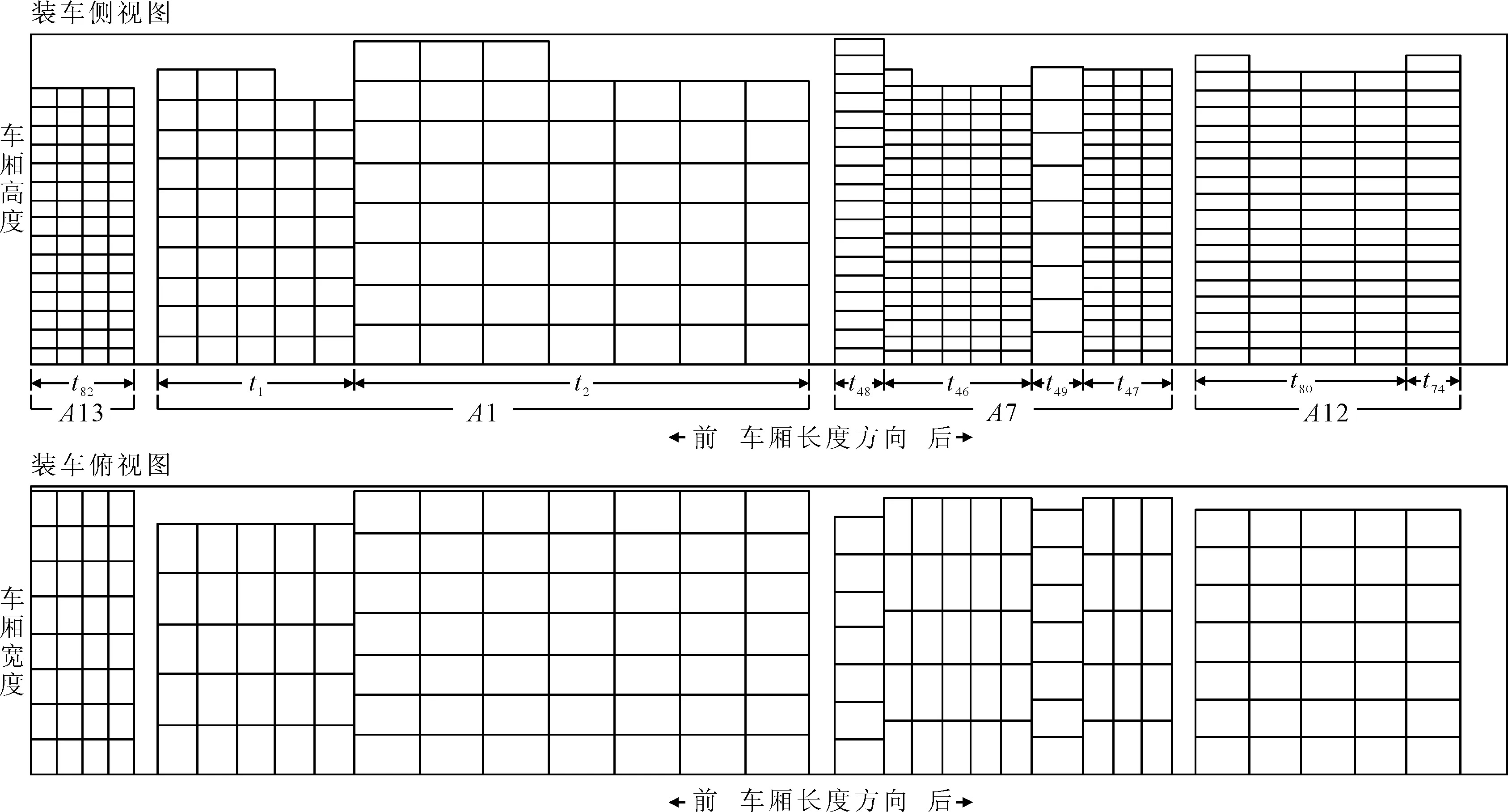
圖1 不同貨物的砌墻法裝車示意圖(注：t為墻厚，A為節點)

本問題的目標是所有車輛總的行程距離最小，沿用三指數車輛流動模型，設置0-1變量xijk，僅當車輛k直接從節點i到節點j，值為1，否則為0.所有的節點構成集合V，S為進入某一路線的節點的集合，顯然S為V的子集，S不能為空且至少包含兩點.

則問題模型如下.

(2)

(3)

(5)

(6)

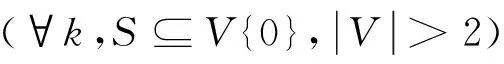
(7)

(8)

(9)

其中：式(3)保證每1節點僅由1輛車拜訪1次；式(4)為節點流量守恒約束，每節點流入與流出的交通量相等；式(5)和(6)保證每臺車在各節點只被使用一次，m臺車輛均從倉庫出發并回到倉庫；式(7)為子回路消除約束，采用集合的形式表示；式(8)保證所取貨物不超過車輛的載重量；式(9)保證裝入車輛中的每種貨物的墻厚合計不超過車廂總長，這也是本問題的特殊之處，裝箱約束條件簡化為一維線性約束，它仍然屬于帶裝箱約束的CVRP問題.

需要注意的是，原始節點下的需求量數據有“大節點”，不滿足本問題模型的式(3)及基本假設.但將每種貨物單獨當成一個節點后，上述模型及假設仍然成立，詳細處理見下節.

3 模型求解

本問題是NP-難問題，對于大規模問題主要采用亞啟發式算法，如禁忌搜索、模擬退火和遺傳算法等亞啟發式算法來求解.

3.1 算法設計

考慮遺傳算法(GA)求解車輛路徑問題的優勢在于它可以隨機地從1個可行解跳到另1個可行解，從而解除其他方法容易陷入局部最優解的困擾[13].此外，GA計算速度快且易與其他算法相結合，適合較大規模的車輛路徑問題.

3.1.1 編碼和解碼

編碼問題是GA算法設計關系到算法效率和質量的首要和關鍵問題，這里設計了一種整數編碼來表示可行的節點排序與車輛指派方案，同時避免了子回路現象.染色體由兩部分組成：第一部分為基于節點的編碼，用來確定節點的訪問先后順序(從左到右)；第二部分為基于車輛的編碼，用來選擇每個節點的訪問車輛.解碼是將染色體轉化為CVRP解的過程.

3.1.2 適應度值計算

對原問題的式(8)～(9)進行松弛，懲罰系數分別為較大的正整數M1,M2，進而得到新的目標函數(見式(10))，并確定該染色體的適應度值(值越小越好).

(10)

3.1.3 初始種群生成

采用完全隨機的方法來構造初始化種群：第一部分編碼為1,2,…,n的隨機排列，第二部分編碼中的每一基因取值為介于1～m之間的隨機整數.

3.1.4 遺傳操作

1) 選擇操作 選擇的實質是對種群中的染色體優勝劣汰.文中采用隨機遍歷抽樣法(SUS)，根據染色體的期望值來實際分配染色體被復制的數目.

2) 交叉操作 這里交叉操作采用單親操作，對于基于節點編碼的基因串采用翻轉(Flip)算子，即將隨機選擇的兩點之間的序列進行翻轉；對于基于車輛編碼的基因串也采用翻轉算子.

3) 變異操作 變異操作也采用單親操作，對于基于節點編碼的基因串采用兩點交換(Swap)算子；對于基于車輛編碼的基因串采用整數變異，即對每一基因以一定的概率用介于1～m之間的其余整數進行替換.

3.2 案例及計算結果

3.2.1 案例數據

循環取貨案例數據來源于某公司市內13個待取貨節點的82種不同尺寸的小體積貨物(平均體積0.03 m3).每節點待取貨物種類從1～15不等(見表1)，平均為6.3種貨物.

案例分別采用2種車型得到2個不同的算例，對于算例a，貨廂內尺寸為L=12 024 mm，W=2 350 mm，H=2 697 mm，容積76.3 m3；算例b，L=8 600 mm，W=2 400 mm，H=2 400 mm，容積49.536 m3.

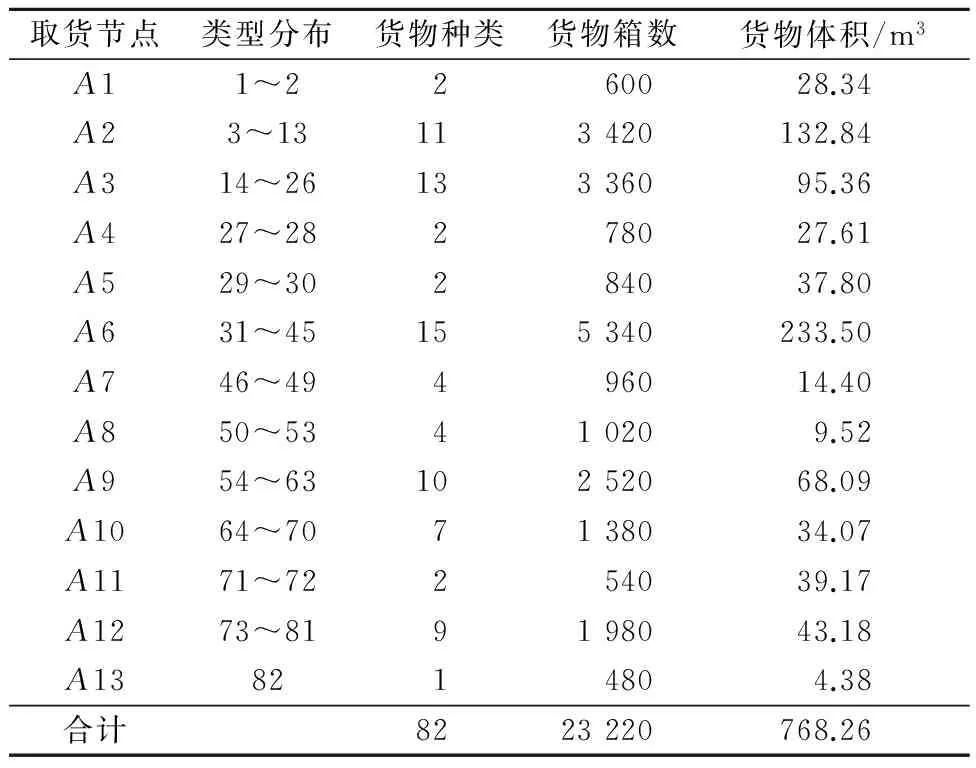
表1 各節點貨物類型分布

3.2.2 大節點及擴展節點分拆

由表1最后一列可知，存在“大節點”，如A6，A2，A3.但這82種小體積貨物每種均沒有超過2種車型的車輛容積，且小于其載重量(滿足式(8))，因此采用砌墻法裝車，每種貨物均可單獨堆碼在一段車廂內.這樣，待裝車的82種貨物擴展為82個不同的地址節點.因為13個原始節點間距離已知，且處于同1個原始節點內的擴展節點之間的兩兩距離為0，則82個擴展節點間的兩兩距離也可得，即cij數據.

3.2.3 最少路線數m的下界

按照式(8)和(9)可分別算得m的下界值，見表2最后4列，所求最優車輛數不會低于這些值.2個算例的主要數據特征見表2.

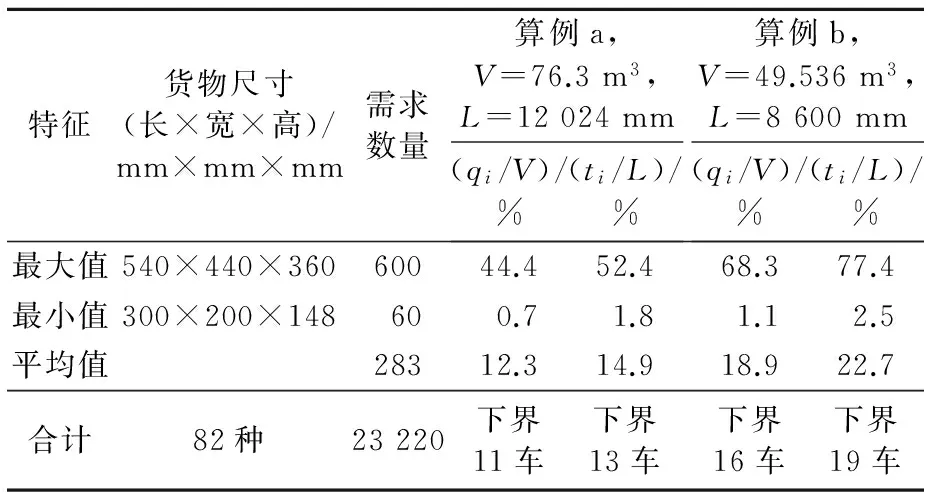
表2 1L-CVRP問題算例主要數據特征

3.2.4 計算環境及結果

文中采用的遺傳算法在Matlab環境下實現，運行于i3-4130/4G配置的64位計算機上.對于式(10)，設置M1=M2=1 000，交叉概率取0.85，變異概率0.05，種群規模設為120，進化代數設為6 000代，最長運行時間控制在600 s內.兩算例計算各運行了15次，最好的計算結果分別見表3～表4.

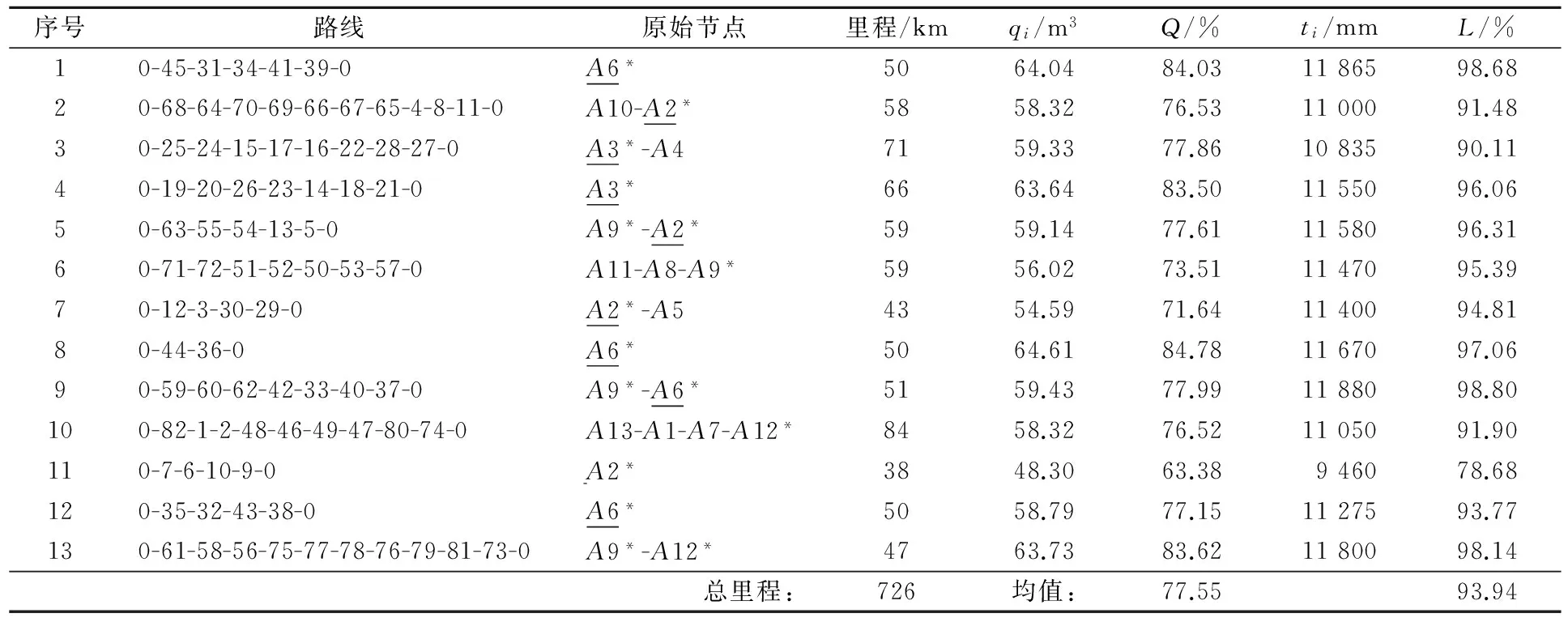
表3 1L-CVRP問題遺傳算法求解最優結果(算例a：V=76.3 m3,L=12 024 mm)

注：*原始節點代號后標有星號的為采用分拆取貨的節點，加下劃線的為大節點，即需求量超過車輛容量，如A6.下表同.

4 分析與討論

4.1 計算結果分析

1) 結果解析 前面是將82種貨物當成節點來計算的，各條路線最終還原成原取貨節點的情況見表3～4第三列所示.其中該列僅1個原始節點的實際上是直達路線，算例a有5條，均是發生在大節點(A2,A3,A6)上；算例b有12條，大節點A2,A3,A6均有直達路線，但A9無直達只是分拆取貨，還有A5,A12 2個未超過車輛容量限制的節點也采用直達送貨且無分拆取貨，因為不同箱子尺寸降低了車輛利用率.

2個算例的主要不同在于車輛尺寸和容量，算例b的車輛更小，在要裝車貨物總量不變的情況下，所用車輛當然更多，路線所訪問的節點數也趨小，采用直達路線的可能性也更高.

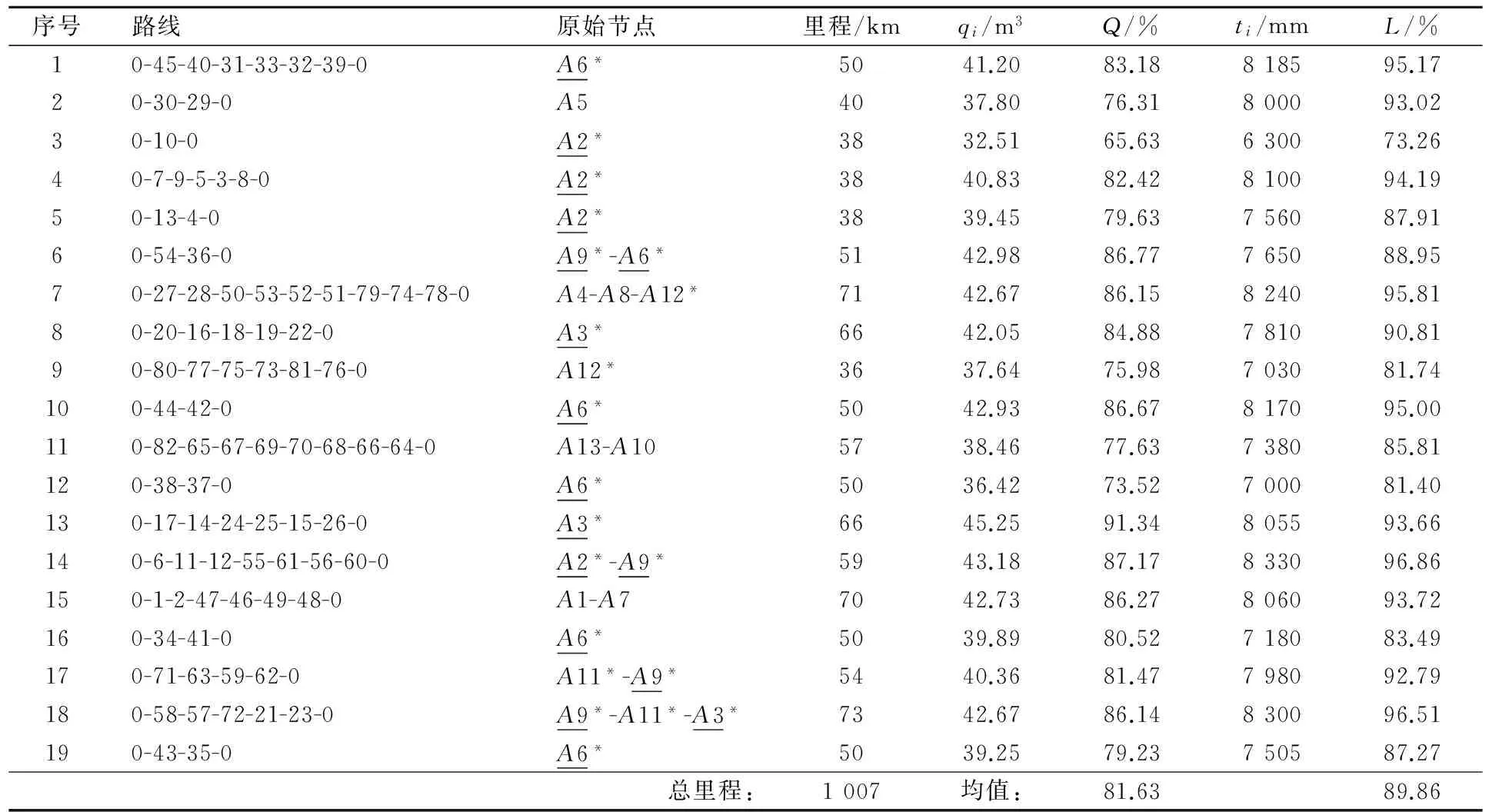
表4 1L-CVRP問題遺傳算法求解最優結果(算例b：V=49.536 m3,L=8 600 mm)

2) 裝箱近似算法的誤差分析 在式(1)的計算中，向上取整時墻厚中的排數為整數，會有些墻的箱子沒裝滿一排而空著(參見圖1裝車側視圖上部的缺口).以算例a為例，研究找到這種最大的空排部分前5個分別是貨物7，33，13，60，1，它們墻厚空檔部分分別占各自ti的21.1%，21.1%，4.8%，22.1%，12.7%，相應占L的2.17%，2.17%，1.88%，1.49%，1.69%，均不超過3%，而且在各自線路中這些誤差均沒有超過最小的ti/L百分比.再比較本文線路容積利用率77.55%的均值，可以確定裝箱近似算法的誤差都不足以影響裝箱和線路的最終結果.

4.2 與相關CVRP問題的不同

注意到表1中有大節點，必須分拆送貨.從表3～4中的分拆節點來看，算例a除3個大節點外，還有非大節點A9,A12被分拆；算例b除4個大節點外還有A11,A12被分拆.文中的大節點涉及到貨物尺寸及裝箱組合，并不能像對待單一體積數據那樣直接減去整車的量，如何拆分這些需求量實際上是1個新的組合問題.SDVRP有專門的算法，但是還沒有涉及到貨物尺寸及裝箱.在這里，同1節點內的不同貨物被當作虛擬節點處理，擴展了節點規模n及相應距離矩陣cij，從另一個角度解決了分拆送貨問題.當然節點規模的增加使得這種處理會犧牲一定的計算時間，總的還是值得的.

與現行的3L-CVRP測試算例相比，本案例為小體積弱異類貨物，數量更多也更符合實際情況；當然3L-CVRP測試算例中貨物常為強異類，數量常為一件，更要考慮精確裝箱，不能用這里的裝箱近似算法.

4.3 應用可行性分析

作為從循環取貨案例中提出的特殊CVRP問題，除了砌墻法裝箱的誤差分析，其可行適用條件也需探討.本例將三維裝箱通過砌墻法簡化為不同于3L-CVRP的單維堆碼長度問題，更便于應用.這里裝車堆碼處理的適用條件是小型弱異類貨物，即單個貨物箱子尺寸相對于車廂尺寸都比較小，且同種貨物數量較多，這樣才能“有磚砌墻”.如果是家電配送大體積且數量少的強異性貨物就難以采取這種方法，但本問題源于實際，有較好的應用意義.

5 結 束 語

針對循環取貨優化決策，結合具體案例的裝車堆碼要求，將車輛路徑問題與裝箱問題綜合考慮，符合當前剛興起的3L-CVRP研究方向，克服了傳統兩類問題孤立研究難以實用化的不足.研究建立了包含容積和堆碼長度的雙約束的CVRP問題模型，并通過擴展節點解決了“大節點”處理的難題.這一問題模型及求解方案符合特定實際情況，比3L-CVRP更簡潔實用.并進行了結果分析與討論，驗證了方案應用的可靠性.

[1]汪金蓮,蔣祖華.汽車制造廠零部件入廠物流的循環取貨路徑規劃[J].上海交通大學學報,2009,43(11):1703-1709.

[2]YI J M, ZHOU J, GAO X L, et al. Tactical planning and optimization of a milk run system of parts pickup for an engine manufacturer[J]. Journal of Southeast University: English Edition,2007,23(增刊1):99-104.

[3]王長瓊,戚小振.三維裝載約束下的汽車零部件循環取貨路徑優化研究[J].武漢理工大學學報(交通科學與工程版),2015,39(6):1161-1165.

[4]王征,胡培祥,王旭坪.帶二維裝箱約束的物流配送車輛路徑問題[J].系統工程理論與實踐,2011,31(12):2328-2341.

[5]GENDREAU M, IORI M, LAPORTE G, et al. A tabu search heuristic for the vehicle routing problem with two dimensional loading constraints[J]. Networks,2007,51(1):4-18.

[6]GENDREAU M, IORI M, LAPORTE G, et al. A tabu search algorithm for a routing and container loading problem[J]. Transportation Science,2006,40(3):342-350.

[7]POLLARIS H, BRAEKERS K, CARIS A, et al. Vehicle routing problems with loading constraints: state-of-the-art and future directions[J]. OR Spectrum,2015,37(2)：297-330.

[8]BORTFELDT A, HOMBERGER J. Packing first, routing second—a heuristic for the vehicle routing and loading problem[J]. Computers & Operations Research,2013,40(3):873-885.

[9]顏瑞,張群,胡睿.考慮三維裝箱約束的多車場車輛路徑問題[J].管理工程學報,2016,30(1):108-116.

[10]ARCHETTI C,SPERANZA M G.Vehicle routing problems with split deliveries[J].International Transactions in Operational Research,2012,39：3-22.

[11]黃文奇,何琨.求解長方體Packing問題的純粹擬人算法[J].中國科學 F輯:信息科學,2009,39(6):617-622.

[12]TOTH P, VIGO D. Vehicle routing: problems, methods, and applications[M]. 2ed.Philadelphia: Society for Industrial and Applied Mathematics,2014.

[13]BAKER B M, AYECHEW M A. A genetic algorithm for the vehicle routing problem[J]. Computers & Operations Research,2003,30(5):787-800.

A Study on a Specific Vehicle Routing Problem Under the Cargo Loading and Stacking by Milk-run Operations

YI Junmin SU Zhixiong

(SchoolofEconomicsandManagement,XiamenUniversityofTechnology,Xiamen361024,China)

A special vehicle routing problem with easy-to-implement loading scheme for route optimizing of a manufacturer’s milk-run operations is proposed with focus on the loading and stacking of weak-heterogeneous small-sized cargos. A new model is formulated with dual capacity constraints on both volume and loading length by applying a wall-building method for cargo stacking inside the vehicle. It is a new variant of the Capacitated Vehicle Routing Problem with Loading Constraints. Besides, the node set is extended temporarily by treating each cargo as a different node, thus an affordable increase in solving time by the node extension is traded with way out the difficulty of node demand surplus vehicle capacity, rather by the method of Split Delivery Vehicle Routing Problem. With slack of the dual-capacity constraints, the fitness value is evaluated using the genetic algorithm, and comprehensive routing and loading results for two instances from real data are achieved. The results are examined with discussions on result analysis, error study of wall-building approximation, model comparison, application conditions, which suggest a sound reliability and feasibility of the model’s application in logistics practice.

vehicle routing problem; loading and stacking; split delivery; genetic algorithm; weak heterogeneity

2016-02-20

*國家自然科學基金項目(71371162)、福建省自然科學基金項目 (2014J01271)資助

U492.3

10.3963/j.issn.2095-3844.2017.02.001

伊俊敏(1969—)：男，博士，教授，主要研究領域為物流系統工程、物流運籌與管理