尺規作圖題新走向
文 /朱廣科
尺規作圖題新走向
文 /朱廣科
中考作圖題已不局限于對基本作圖技能的考查,取而代之的是一批立意活潑、設計新穎、富有創意的作圖題.該類作圖題大都聯系生活實際,要求學生必須進行多方位、多角度、多層次探索,以檢驗思維的靈活性、發散性、創新性.現以2016年中考試題為例,就各種創新題分類說明,供你復習時參考.
一、圖形剪拼型
例1(2016年荊州卷)請用割補法作圖,將一個銳角三角形經過一次或兩次分割后,重新拼成一個與原三角形面積相等的平行四邊形(只要求用一種方法畫出圖形,把相等的線段作相同的標記).
解:如圖1所示.
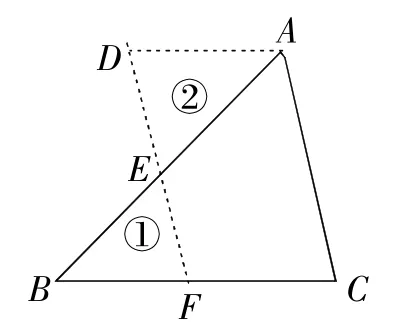
圖1
AE=BE,DE=EF,AD=CF.
點評:解答剪拼問題需要進行多方位、多角度、多層次的探索,能培養思維的靈活性、發散性和創新性.
二、圖形變換型
例2(2016年昆明卷)如圖2,△ABC三個頂點的坐標分別為A(1,1),B(4,2),C(3,4).
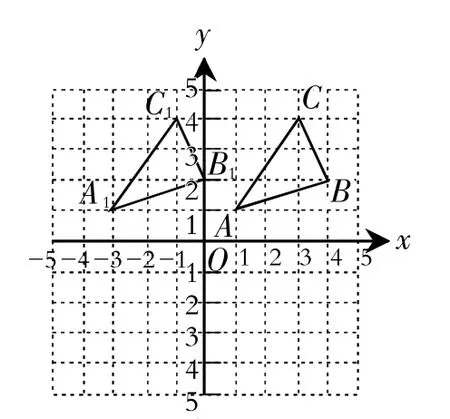
圖2
(1)請畫出將△ABC向左平移4個單位長度后得到的圖形;
(2)請畫出△ABC關于原點O成中心對稱的圖形;
(3)在x軸上找一點P,使PA+PB的值最小,請直接寫出點P的坐標.
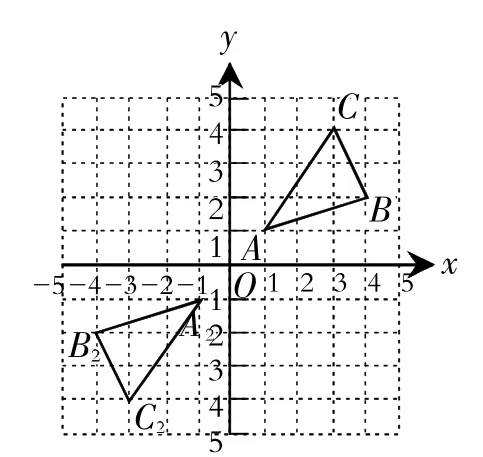
圖3
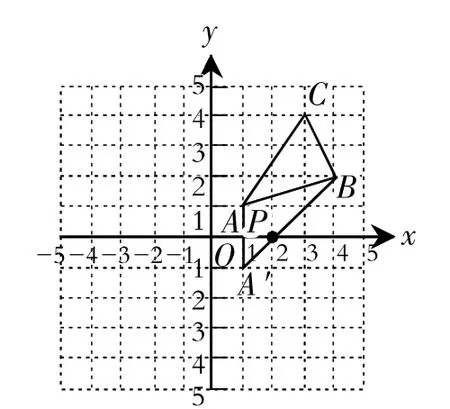
圖4
責任編輯:王二喜
解:(1)如圖2所示.
(2)如圖3所示.
(3)找出A的對稱點A′(-1,-1),連接BA′,與x軸交點即為P,如圖4所示,點P的坐標為(2,0).點評:觀察并挖掘變換條件,根據圖形的性質得出對應點位置.
三、利用網格的特征作圖
例3(2016年溫州卷)如圖5,在方格紙中,點A,B,P都在格點上.請按要求畫出以AB為邊的格點四邊形,使P在四邊形內部(不在邊界上),且P到四邊形的兩個頂點的距離相等.
(1)畫出一個?ABCD;
(2)畫出一個四邊形ABCD,使∠D=90°,且∠A≠90°.
解:(1)如圖5.(2)如圖6.
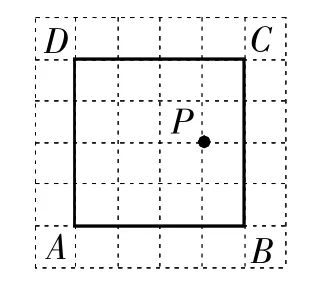
圖5
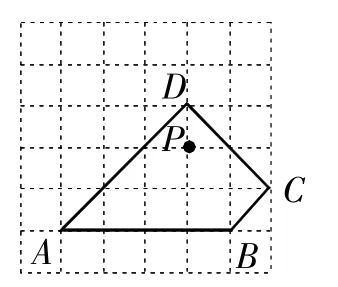
圖6
點評:利用網格線的結構特征和相似三角形對應邊成比例找出對應點.
四、開放探究型
例4(2016年廣安卷)在數學活動課上,老師要求學生在5×5的正方形ABCD網格中(小正方形的邊長為1)畫直角三角形,要求三個頂點都在格點上,而且三邊與AB或AD都不平行.畫四種圖形,并直接寫出其周長(所畫圖象相似的只算一種).
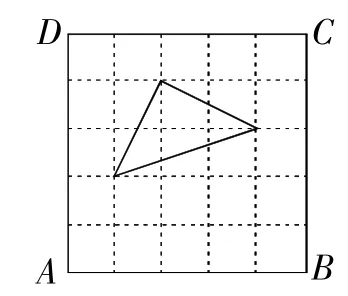
圖7
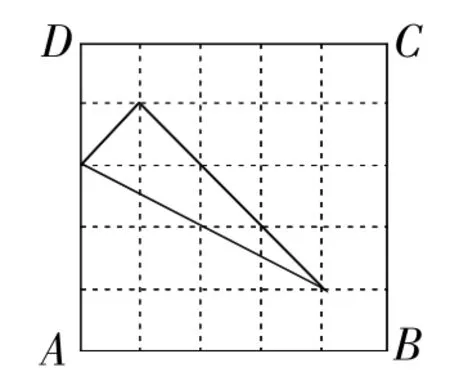
圖8
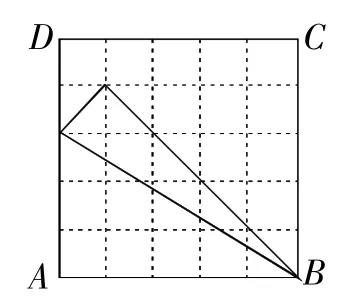
圖9
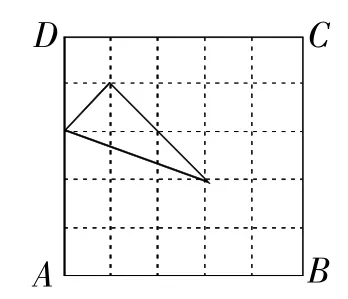
圖10
點評:對于結論不確定的問題,解題思路不同,推導深入程度不同,將得到不同的結論,它們均可作為問題的答案.
五、閱讀理解型
例5(2016年連云港卷)光反射時,反射光線、入射光線和法線在同一平面內,反射光線、入射光線分別在法線兩側,反射角等于入射角.如圖11,AO為入射光線,入射點為O,ON為法線(過入射點O且垂直于鏡面的直線),OB為反射光線,此時反射角∠BON等于入射角∠AON.
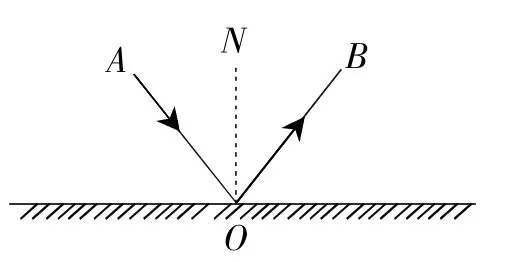
圖11
問題思考:(1)如圖12,一束光線從點A處入射到平面鏡上,反射后恰好過點B,請在圖中確定平面鏡上的入射點P,保留作圖痕跡,并簡要說明理由;

圖12
(2)如圖13,兩平面鏡OM、ON相交于點O,且OM⊥ON,一束光線從點A出發,經過平面鏡反射后,恰好經過點B.小昕說,光線可以只經過平面鏡OM反射后過點B,也可以只經過平面鏡ON反射后過點B.除了小昕的兩種做法外,你還有其他做法嗎?如果有,請在圖中畫出光線的行進路線,保留作圖痕跡;
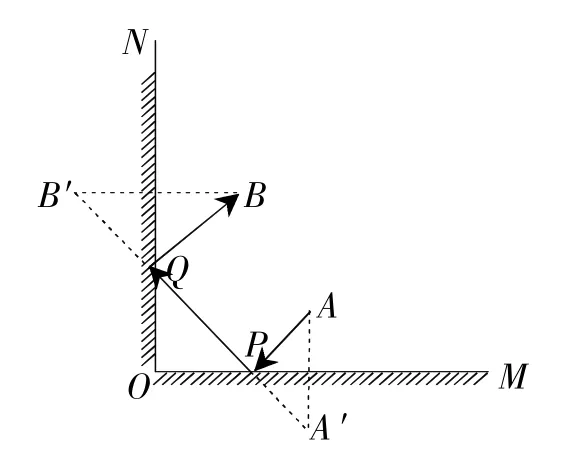
圖13
問題拓展:(3)如圖14,兩平面鏡OM、ON相交于點O,且∠MON=30°,一束光線從點S出發,且平行于平面鏡OM,第一次在點A處反射,經過若干次反射后又回到了點S,如果SA和AO的長均為1m,求這束光線經過的路程.
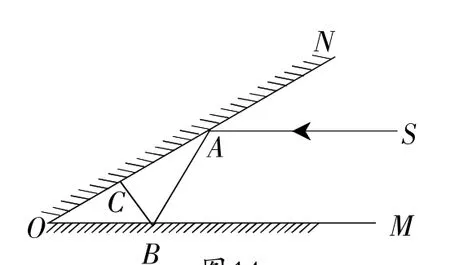
圖14
解:(1)如圖12,作A關于平面鏡ML的對稱點A′,連接A′B交ML于點P,則點P為所求.
證明:如圖12,作PN⊥ML,
∵A與A′關于ML對稱,∴∠1=∠2,
∵∠2+∠3=90°,∠1+∠2+∠3+∠4=180°,
∴∠1+∠4=90°,∴∠3=∠4,
∴AP是入射光線,PB是反射光線,即P為入射點.
(2)如圖13,作A關于OM的對稱點A′,作B關于ON的對稱點B′,連接A′B′,分別交OM、ON于點P、Q.光線的行進路線為A→P→Q→B.
(3)如圖14,光線的行進路線為S→A→B→C→B→A→S.
∵∠SAN=∠OAB=∠MON=∠30°,∴OB=BA,
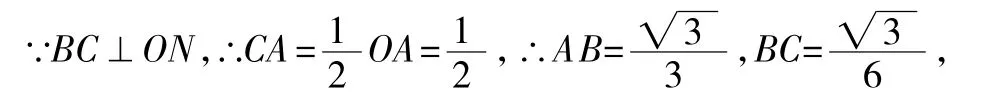
∴這束光線經過的路程為:SA+AB+BC+CB+BA+AS=
點評:理解光的反射定律與軸對稱關系,正確作圖是解題的關鍵.

