內空和充水管道在爆炸沖擊荷載下的數值模擬分析

房 沖

(解放軍理工大學，江蘇 南京 210007)

?

·水·暖·電·

內空和充水管道在爆炸沖擊荷載下的數值模擬分析

房 沖

(解放軍理工大學，江蘇 南京 210007)

利用ANSYS/LS-DYNA有限元軟件,根據實驗目的建立了計算模型，并選取適當的本構關系和材料，對空中TNT炸藥爆炸沖擊荷載下的內空和充水管道的動力響應規律進行了數值模擬分析，指出爆炸沖擊荷載下，在等量炸藥的條件下，充水管道的變形量、單元位移及單元壓強峰值較內空管道低，這些參數的增加速率也均低于內空管道；充水管道的抗變形能力更強，穩定性更高。

爆炸沖擊，充水管道，動力響應，計算模型

0 引言

目前，工程埋地管線的試驗研究和模擬計算比較多，針對空爆條件下管道的研究較少。充水管道(充水管)和內空管道(內空管)在空中爆炸沖擊荷載下的動力響應是一個重要的研究方向。Ma等[1]對金屬管道在內充水條件下受到的沖擊進行實驗，認為管道中內充水可耗散部分沖擊能量，同時提高管道的初始破裂臨界速度。紀沖等[2]通過對充液及內空圓柱殼在爆炸沖擊下的動力響應和屈曲特性進行了實驗和模擬，表明充液圓柱殼在抗爆炸沖擊方面較內空圓柱殼提高很大。內空和充水管道在爆炸沖擊荷載下的動力響應及變化規律還有待研究。目前，此類問題大多采用有限元方法來求解，可利用ANSYS/LS-DYNA軟件對管道在空中爆炸沖擊荷載下的動力響應進行數值模擬[3,4]。

1 材料模型及狀態方程參數

數值模擬采用ANSYS/LS-DYNA軟件中的材料模型及相應狀態方程。

1.1 空氣、水材料模型及狀態方程

空氣及水均采用提供的空白材料模型，空氣的狀態方程為：

P=(γ-1)ρe0/ρ0

(1)

其中，γ為絕熱指數，γ=1.40；e0為氣體比內能，e0=0.25 MPa；ρ0為空氣初始密度,ρ0=1.25×10-3g/cm3。水的狀態方程[5]為：

(2)

其中，C,S1，S2，S3，a，E均為相關參數;μ=ρ/ρ0-1;C=1 480 m/s，S1=2.56，S2=1.986，S3=0.00，γ0=0.50,a=0.00。

1.2 炸藥材料模型及狀態方程

TNT炸藥采用高能炸藥模型及JWL狀態方程，爆轟產物壓力P表示的JWL狀態方程[6]為:

(3)

其中,V為相對體積;ρ為炸藥密度;E0為單位體積炸藥內能；A，B，R1，R2，ω均為相關參數。TNT炸藥及JWL狀態方程參數為:ρ=1 640 kg/m3，E0=7.0×109J/m3,A=374 GPa，B=3.23 GPa，R1=4.15，R2=0.95，ω=0.30。

1.3 管道材料模型

管道選用X70鋼材料，采用彈塑性模型，該模型遵從Von-Mises屈服準則[7，8]，其表達式為：

(4)

其中，σ為應力;E為彈性模量;Et為切線模量;σe為屈服應力;ε,εe分別為應變和彈性極限應變。物理力學參數為：ρ=7 830 kg/m3，ω=0.30，E=3.23 GPa，σe=289 MPa，Et=500 MPa。

2 管道動力響應計算模型

建立管道動力響應的計算模型。設坐標軸原點O點為管道中心，X軸為水平方向，Y軸為豎直方向，Z軸與管道軸中心軸向重合且向外為正方向。模型各材料位置如圖1所示，管道內分別充水和空氣兩種介質。

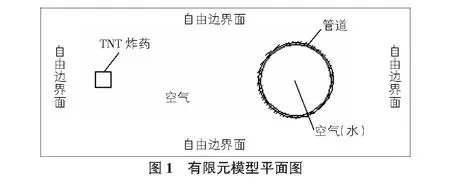
該模型共進行8種工況下的模擬計算，分析充水管道在不同炸藥量爆炸沖擊荷載下的動力響應問題，各工況編號及詳細參數如表1所示。

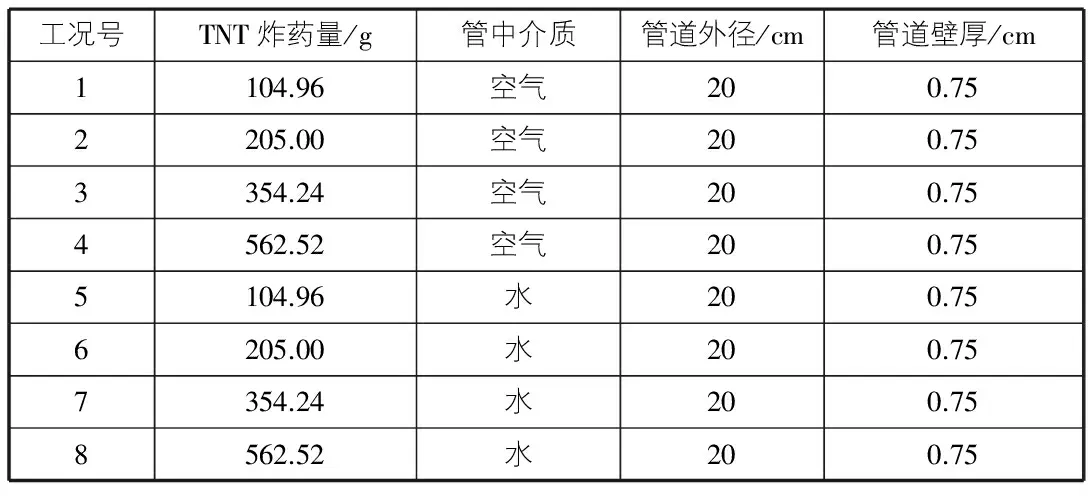
表1 模型參數表

TNT炸藥、空氣、水和管道均采用Solid164六面體網格進行劃分，炸藥、空氣、管道內部空氣(水)采用ALE算法，管道選擇采用LANGANGIAN算法。選用流固耦合方法，將炸藥、空氣和管道內部空氣(或水)與管道耦合在一起進行模擬計算[9]。

3 模擬計算結果與分析

利用ANSYS軟件對所建立的模型進行模擬計算，得到管道在空中爆炸沖擊荷載下的數值模擬結果。

3.1 管道模擬結果與分析

通過LS-PrePost軟件查看工況3和工況7的模擬結果，最終變形如圖2所示。

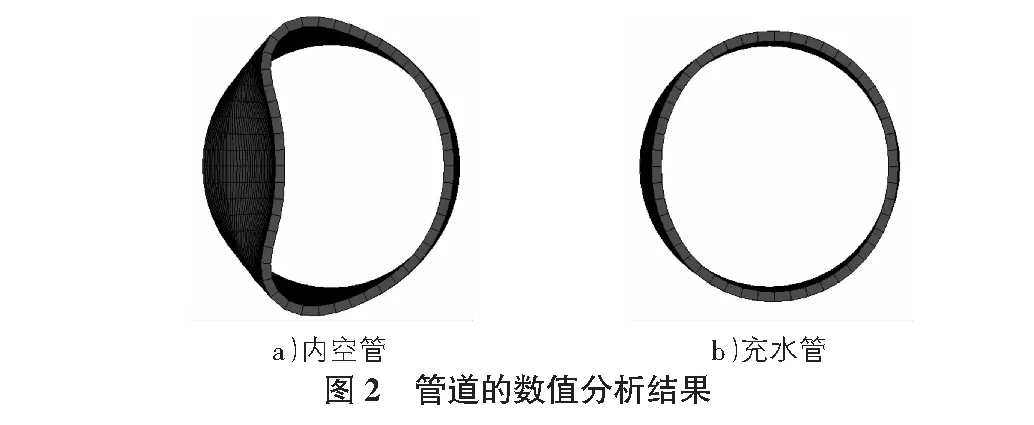
顯然，充水管道的變形遠小于內空管道，這說明：在爆心距一定的條件下，管道內部的水介質對抵抗管道在爆炸沖擊荷載下的變形有很大的作用。

3.2 管道位移過程與分析

在截面上選取4個單元，單元編號及單元位置如圖3所示。

以工況3為例，分別做出四個單元合位移時程曲線，如圖4所示。

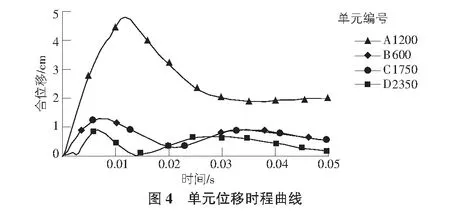
由圖4可知：位移先是快速增長，在0.012 s處達到峰值4.83 cm，接著緩慢下降，在2 cm左右達到穩定，這說明：管道已經產生了塑性變形，不能完全恢復。

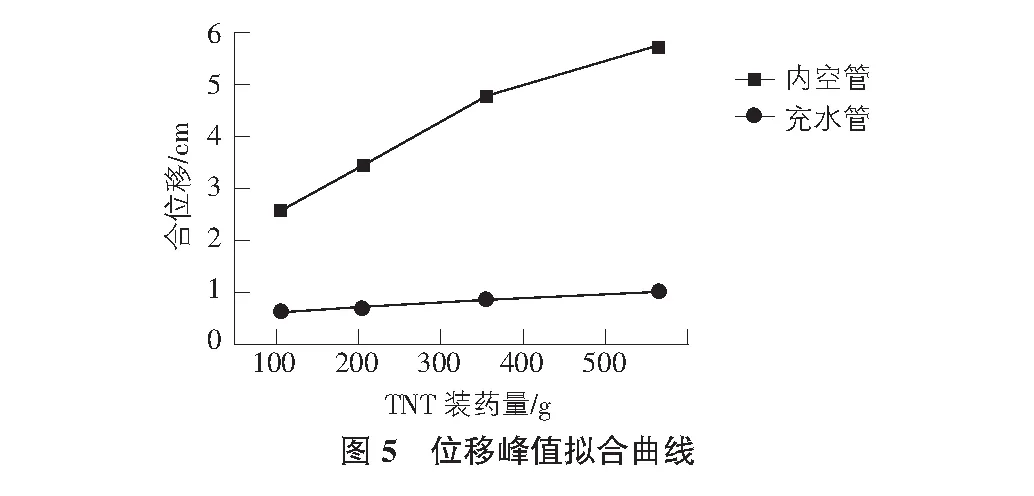
圖5為兩組模型的單元位移峰值的擬合曲線。由圖可知：在等量TNT炸藥爆炸沖擊荷載作用下，充水管的單元位移峰值不到空管的1/4；炸藥量由104.96 g增加到562.52 g，空管單元位移峰值由2.57 cm增加到5.75 cm，充水管單元位移峰值僅增加了0.38 cm，空管的單元位移隨炸藥增加的速率是充水管的9倍。這說明：充水管單元位移峰值受炸藥量變化的影響遠小于空管。由于水介質的不可壓縮性，在一定程度上削弱了管道受到的沖擊荷載，管內空氣介質的削弱作用遠小于水介質，因而管道內充水能顯著降低管道的位移，充水管穩定性高于空管。

3.3 管道壓強過程與分析

通過模擬計算出管道在爆炸沖擊荷載下的壓強，分析8種工況下壓強可知：在炸藥量一定的情況下，空管壓強變化差值大于充水管的壓強變化差值，充水管的壓強作用時間比空管長；同時，可得到管道在各工況下的峰值壓強，其中，迎爆面的單元峰值壓強最大，背爆面壓強變化最為劇烈，上下兩端的壓強較為平穩。

通過分析8種工況下的峰值壓強可得壓強峰值擬合曲線，如圖6所示。

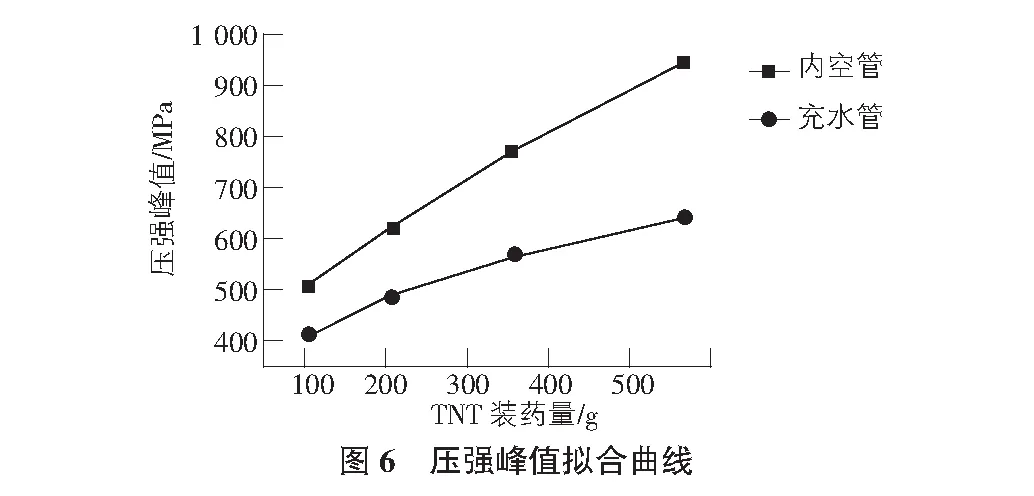
由圖6可知：在等炸藥量的條件下，空管單元壓強峰值較充水管高；隨著炸藥量的增加，空管的單元壓強峰值增長速率高于充水管，這說明：管道內部充水對其在爆炸荷載下受到的壓強影響較大。

4 結語

1)空管在爆炸沖擊荷載下的變形較充水管要大。內部充水情況下，管道的抗變形能力顯著提高。2)在等量炸藥爆炸沖擊荷載下，空管的單元位移峰值遠大于充水管；隨著炸藥量的增加，空管的單元位移峰值增加速率高于充水管。管道充水能有效降低管道的單元位移峰值及位移峰值增加速率，增強管道的穩定性。3)管道壓強峰值出現在管道迎爆面上，在等量炸藥爆炸沖擊荷載下，空管的壓強峰值增加速率高于充水管，管道內充水對管道的壓強峰值影響較大。

[1] Ma X Q,Stronger W J.Spherical missile impact and perforation of filled tubes[J].International Journal of Impact Engineering,1988,3(1):1-16.

[2] 紀 沖,龍 源,劉 影,等.充液及內空圓柱殼在爆炸荷載下動力屈曲特性研究[J].振動與沖擊,2014,33(2):76-80,88.

[3] 錢七虎，王明洋，趙躍堂.爆炸波作用下三相飽和土中不動障礙物上的荷載[J].爆炸與沖擊,1994,14(3):97-104.

[4] 趙長嘯，龍 源，紀 沖,等.土中爆炸沖擊作用下埋地管道動力響應數值模擬研究[J].綜述與爆破理論，2010(3)：45.

[5] 李曉杰，張程嬌，王小紅，等.水的狀態方程對水下爆炸影響的研究[J].工程力學,2014,31(8):46-53.

[6] 王 輝.炸藥爆炸產物JWL狀態方程參數數值計算[D].西安：西安工業大學，2011.

[7] 都的箭，梁雪瑩，鄧正棟，等.埋地管線爆炸地沖擊作用下解析解計算研究[J].爆破,2011,28(3):21-25.

[8] 楊 政，郭萬林，董惠茹，等.X70管線鋼靜態和動態韌性試驗研究[J].西安交通大學學報,2003,37(5):488-491.

[9] 姚安林，趙師平，么惠全，等.地下爆炸對埋地輸氣管道沖擊響應的數值分析[J].西安石油大學學報,2009,31(4):168-172.

1009-6825(2017)11-0130-03

2017-02-08

房 沖(1991- )，男，在讀碩士

O383.1

A