基于細觀混凝土模型的剛性彈體正侵徹彈道偏轉分析*

鄧勇軍，陳小偉，姚 勇，楊 濤

(1.西南科技大學土木工程與建筑學院，四川 綿陽 621000；2.中國工程物理研究院總體工程研究所，四川 綿陽 621999)

基于細觀混凝土模型的剛性彈體正侵徹彈道偏轉分析*

鄧勇軍1,2，陳小偉1,2，姚 勇1，楊 濤1

(1.西南科技大學土木工程與建筑學院，四川 綿陽 621000；2.中國工程物理研究院總體工程研究所，四川 綿陽 621999)

為研究混凝土細觀因素對剛性彈正侵徹彈道偏轉的影響，基于骨料隨機投放的思路建立混凝土三維細觀幾何模型，分析剛性彈正侵徹過程中發生彈道偏轉的原因及可能影響因素，定量討論混凝土細觀因素對彈道偏轉的影響。結果表明：混凝土細觀數值模型可以較好地反映彈體正侵徹過程中彈道偏轉等典型物理現象，且細觀參數對于彈體彈道偏轉有顯著影響。剛性彈正侵徹細觀混凝土時，存在一個彈體直徑/骨料最大粒徑比的特征比值。

混凝土;細觀建模;剛性彈;正侵徹;彈道偏轉

混凝土材料由于其抗壓強度較高、原料豐富及耐久性好等特點，被廣泛應用于高壩、橋梁、核電站、機場跑道、公路及其他防護工程等重要基礎設施建設。該類結構在使用過程中，除受常見的靜力荷載、地震作用，在戰爭或恐怖襲擊中還可能遭受彈體的侵徹爆炸作用。

侵徹過程是一個彈/靶相互作用的瞬態接觸問題，目前在彈/靶侵徹理論、數值計算、實驗等方面已做了大量研究，對混凝土靶侵徹問題已有較深刻認識[1-8]。已有文獻中大多將混凝土視作均勻材料，無法考慮混凝土組成成分對侵徹過程的影響。一般而言，混凝土是典型的多相非均質復合材料，主要由粗骨料、水泥水化物及骨料與水泥砂漿粘結帶等組成[9]，各相材料性質差異較大。即使是嚴格的剛性彈正侵徹，由于混凝土隨機因素作用，彈體可能受到非對稱力作用從而發生彈道偏轉。若計算中將混凝土當作均勻材料分析，無法反映侵徹過程中彈體與骨料/砂漿的相互作用，以及彈體彎曲破壞、彈道偏轉等典型的物理現象[10]。計算機性能的提高,使得從混凝土細觀層次出發對該類問題進行數值模擬成為可能。建立反映混凝土細觀組成的數值模型，能較直觀地分析侵徹過程中彈體受力特點及侵徹規律，對改進彈體的侵徹效應及提高結構的防護能力有重要意義。

本文中，采用骨料隨機投放思想，建立混凝土三維細觀幾何模型，并參考侵徹實驗對模型有效性進行驗證。從混凝土細觀組成分析剛性彈正侵徹過程中彈道偏轉的原因及可能影響因素。然后以彈體偏轉角度為指標，研究混凝土細觀因素(骨料隨機分布、骨料強度、砂漿強度等)，彈體直徑/骨料最大粒徑比，以及侵徹速度對彈體偏轉角度的影響。最后給出混凝土細觀模型和均勻模型分別用于彈體侵徹數值模擬的適用范圍。

1 混凝土細觀數值模型建立

Z.M.Wang等[11]提出混凝土隨機骨料模型，將混凝土視作由骨料、水泥砂漿以及兩者之間的粘結帶組成的三相非均質復合材料，采用骨料隨機投放思路，實現混凝土的細觀數值建模。本文在該模型的基礎上，基于混凝土級配理論，建立細觀混凝土模型，具體步驟如圖1所示。

1.1 隨機數產生

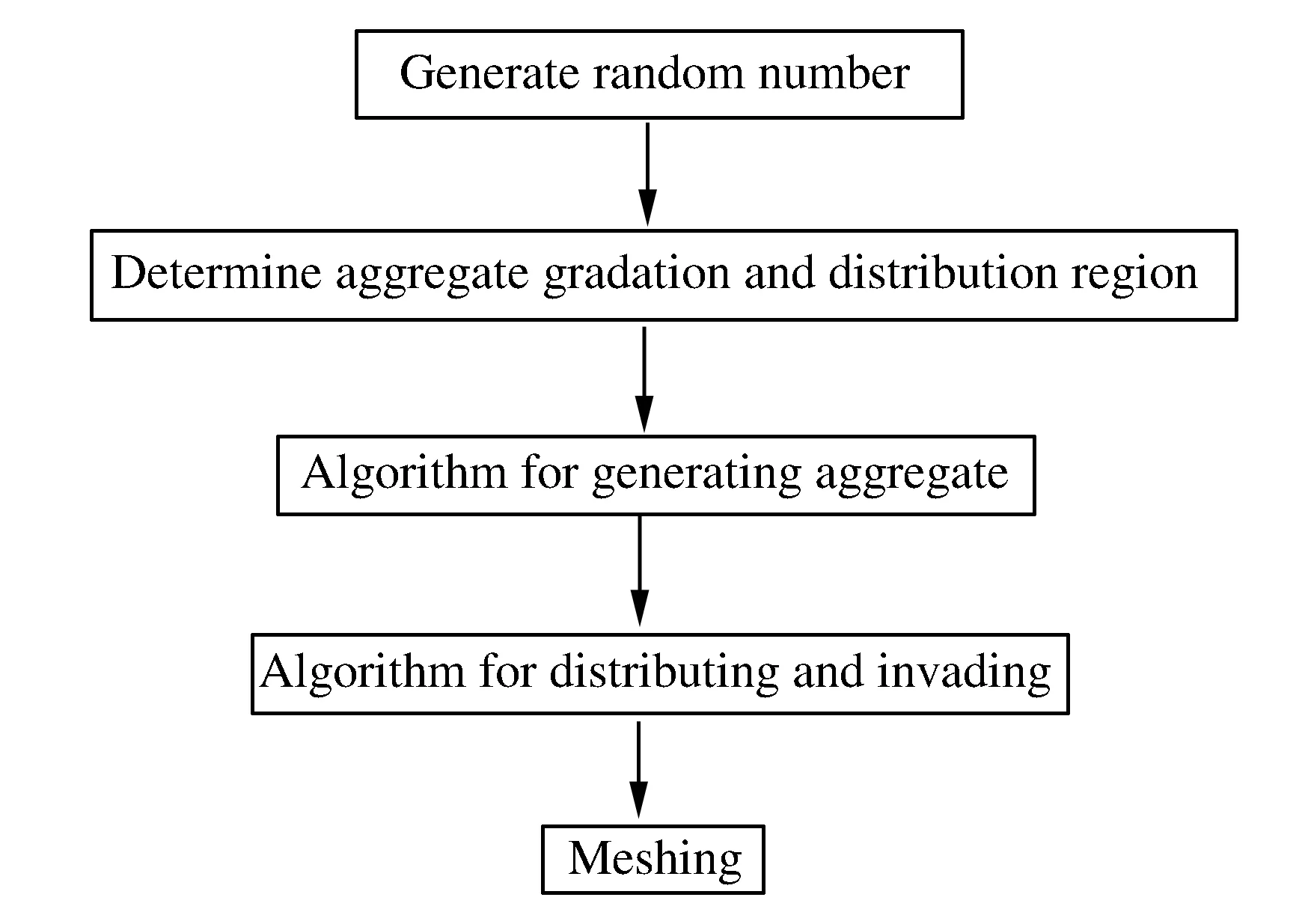
圖1 細觀模型建立流程圖Fig.1 Flow diagram of meso-scopic modeling

模型中骨料位置的隨機分布，根據蒙特卡羅法在計算機中生成的偽隨機數來確定。采用VC++6.0在區間[0,1]上產生均勻分布的偽隨機數X，然后給定區間上均勻分布的隨機數序列，作為后續骨料投放的坐標基點。

1.2 骨料級配及投放區域的確定

工程材料或結構中，混凝土骨料的粒徑分布區間廣泛，且骨料粒徑差別對于侵徹彈體受力影響較大，因此細觀模型中應考慮混凝土的級配組成。根據混凝土所含骨料粒徑范圍，通常可分為一、二、三、四級配混凝土。參考W.B.Fuller等提出的三維級配曲線[12]，可以得到常用的幾種級配骨料分布，如表1所示，Vs∶Vm∶Vb∶Vh為混凝土中小、中、大、巨大骨料的體積分數之比。

表1 不同級配骨料粒徑分布

根據表1計算出不同尺寸試件中各種粒徑的骨料顆粒數(其中粒徑小于5 mm的骨料顆粒計入砂漿中)，然后根據骨料的投放區域生成幾何模型。模型投放區域通過空間直角坐標系及柱坐標系實現，如：生成立方體試件，則采用空間立方體投放區域；生成圓柱體試件，則采用空間圓柱體投放區域。

1.3 骨料生成算法

根據實際碎石混凝土中骨料的特點，采用隨機凸多面體模擬骨料的三維幾何形狀。此處的隨機凸多面體以八面體骨料基為基礎生長而成，并結合文獻[13]，采用空間體積為標度對新生成頂點的位置進行控制，實現骨料形狀為凸型骨料。

1.4 骨料投放算法

三維隨機骨料在投放過程中為保證投放域內的骨料不會發生相互侵入的現象，采用點侵入凸多面體空間的判斷、凸多面體空間侵入的特殊情況[13]對生成的多面體進行判斷。根據上述隨機多面體骨料的生成及投放算法，利用VC++6.0軟件編制了三維隨機凸面體骨料模型的程序3D-RAM。利用該程序生成的全集配混凝土骨料含量如圖2所示。

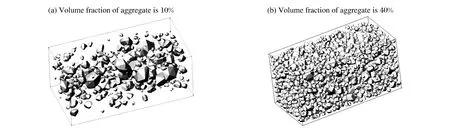
圖2 骨料投放示意圖Fig.2 Schematic diagram of aggregate distribution

1.5 網格劃分

有限元網格剖分是混凝土三維細觀模型建立的難點。本文中采用背景網格劃分法[14]進行混凝土各相介質的網格劃分。具體步驟如下：基于背景網格，對骨料、砂漿及界面進行投影，圖3(a)中網格分為骨料、砂漿、界面共3類。考慮骨料、砂漿及界面三相材料，如果某個單元的8個節點均落入骨料的投影范圍內，則該單元類型為骨料單元。若單元的8個節點均落入砂漿區域內，則該單元的類型為砂漿單元。若單元的8個節點既有落入骨料范圍又有落入砂漿范圍的，則該單元為界面單元。三者之間采用共節點方式處理，此時界面單元的厚度為1個單元厚度(本文中單元最小尺寸為2 mm)。最終得到混凝土細觀模型各組成部分如圖3(b)～(d)所示。

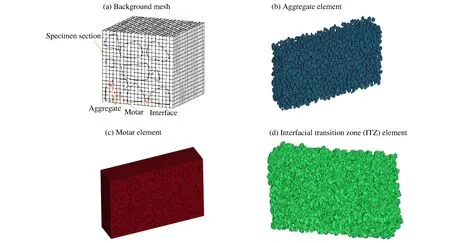
圖3 細觀模型各組成部分有限元剖分Fig.3 Each component’s FEM of meso-scopic model

2 數值模型有效性驗證

通過彈/靶侵徹實驗與數值模擬的對比，對以上建立的混凝土細觀數值模型用于分析沖擊問題的有效性進行驗證，計算通過LS-DYNA有限元軟件實現。

2.1 混凝土靶侵徹實驗模擬

選取S.J.Hanchak等[15]的實驗為驗證分析對象，計算中彈體形狀及靶板尺寸與文獻中保持一致，實驗中彈體未直接作用在鋼筋上，因此數值模型中不考慮鋼筋的作用。

混凝土單軸抗壓強度為48 MPa，采用細觀模型，最大骨料粒徑為9.5 mm。對彈體采用MAT_RIGID模型；對骨料、砂漿及界面均采用K&C模型。計算中采用侵蝕判斷準則作為單元的失效準則。相關模型參數見表2,表2中ρ為密度，E為彈性模量，μc為泊松比，σt為拉伸強度，σc為壓縮強度。

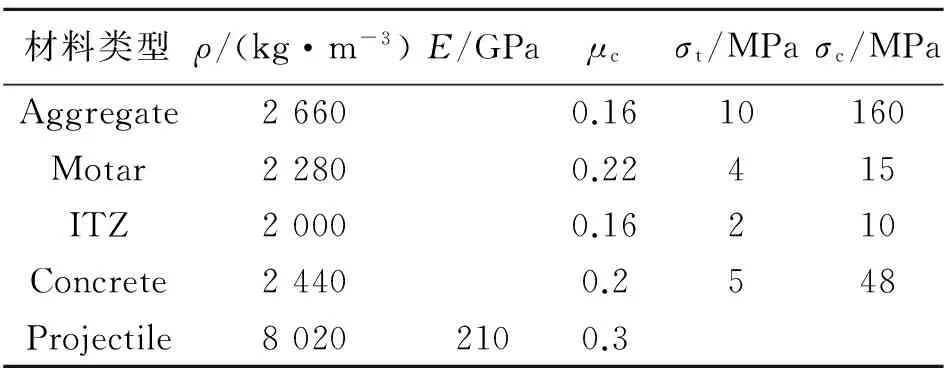
表2 彈體及混凝土材料參數

表3給出了不同沖擊速度v0下，數值模擬和實驗得到的彈體剩余速度vr。從表3可以看出，數值計算的彈體剩余速度與實驗值的相對誤差在10%以內，且靶板宏觀破壞模式與實驗現象也較一致，如圖4所示。這表明本文中所建立的混凝土細觀模型可有效用于彈體侵徹模擬問題。

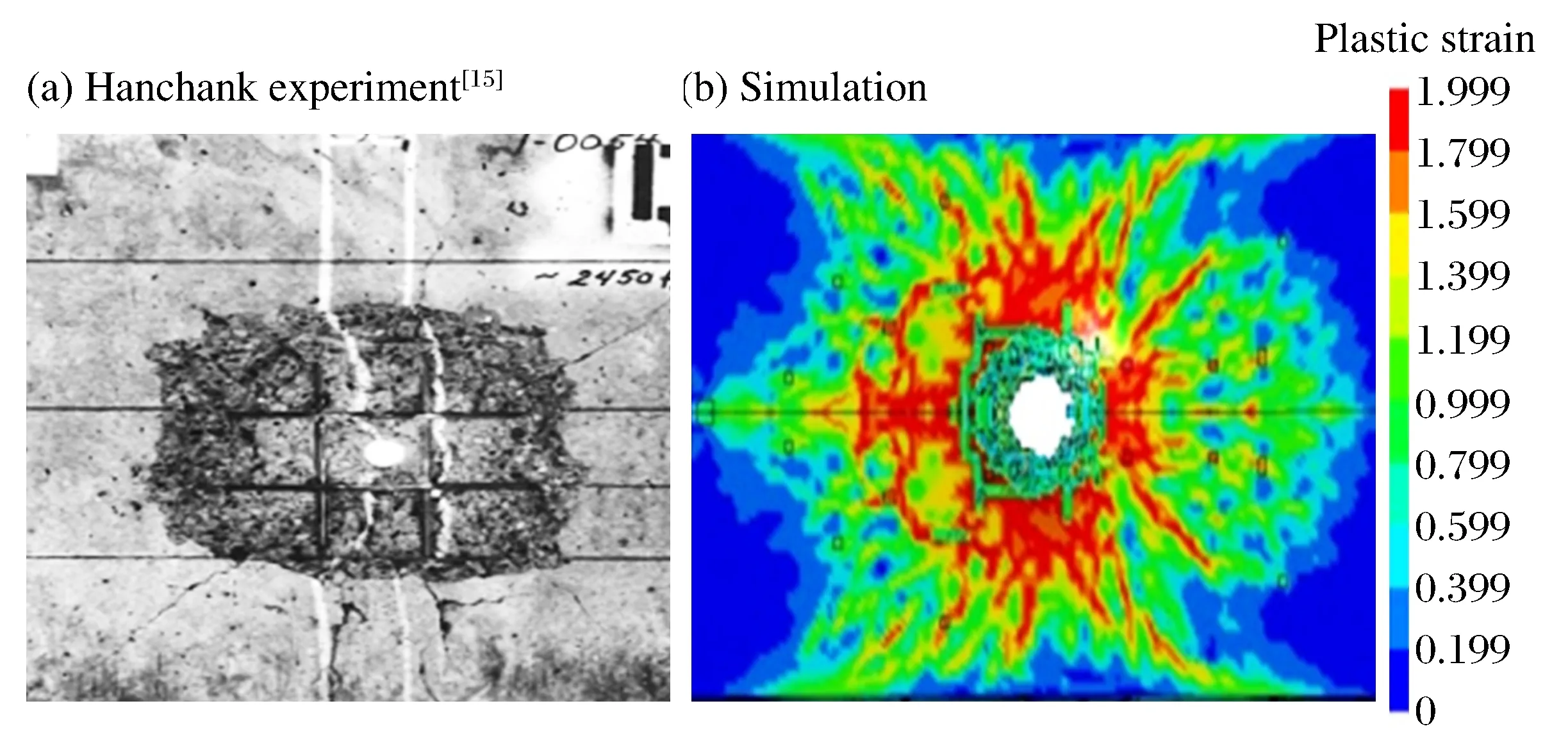
圖4 靶板迎彈面破壞模式Fig.4 Failure mode of the target on the impact side

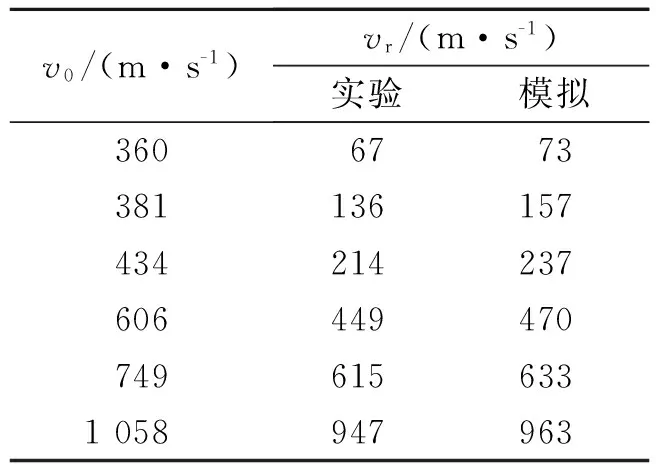
v0/(m·s-1)vr/(m·s-1)實驗模擬36067733811361574342142376064494707496156331058947963

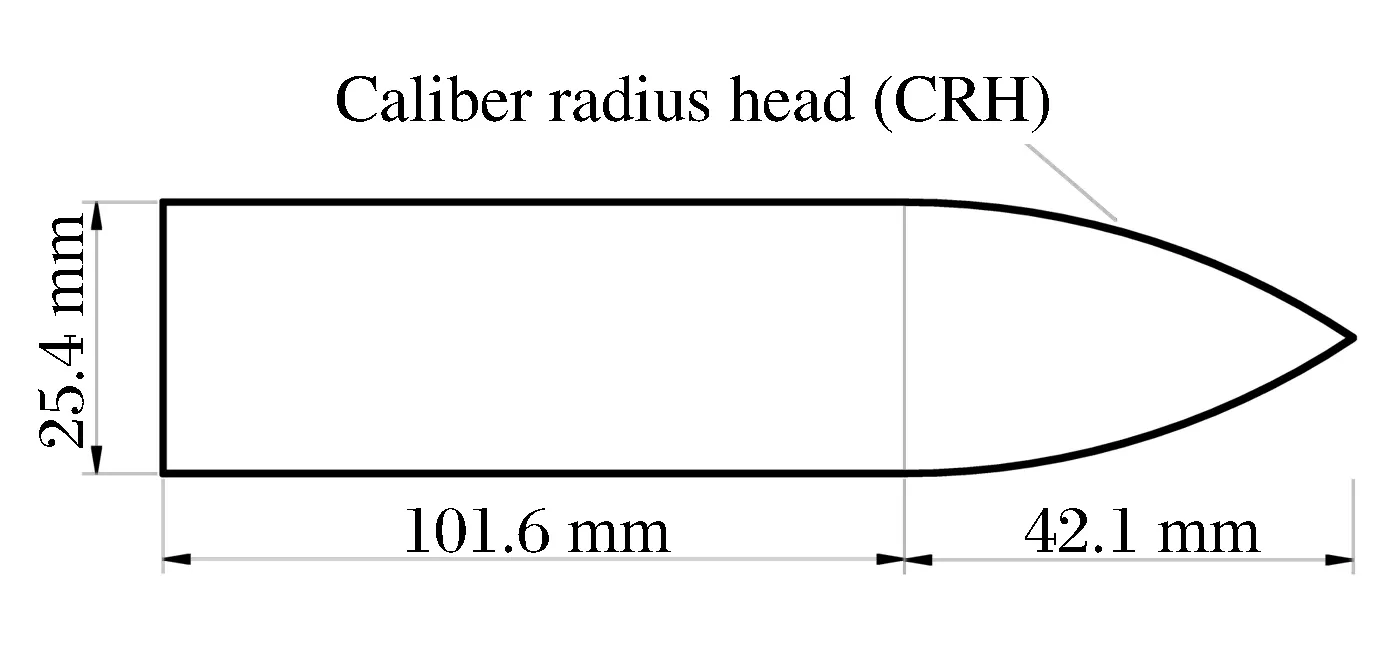
圖5 彈體尺寸Fig.5 Projectile geometry

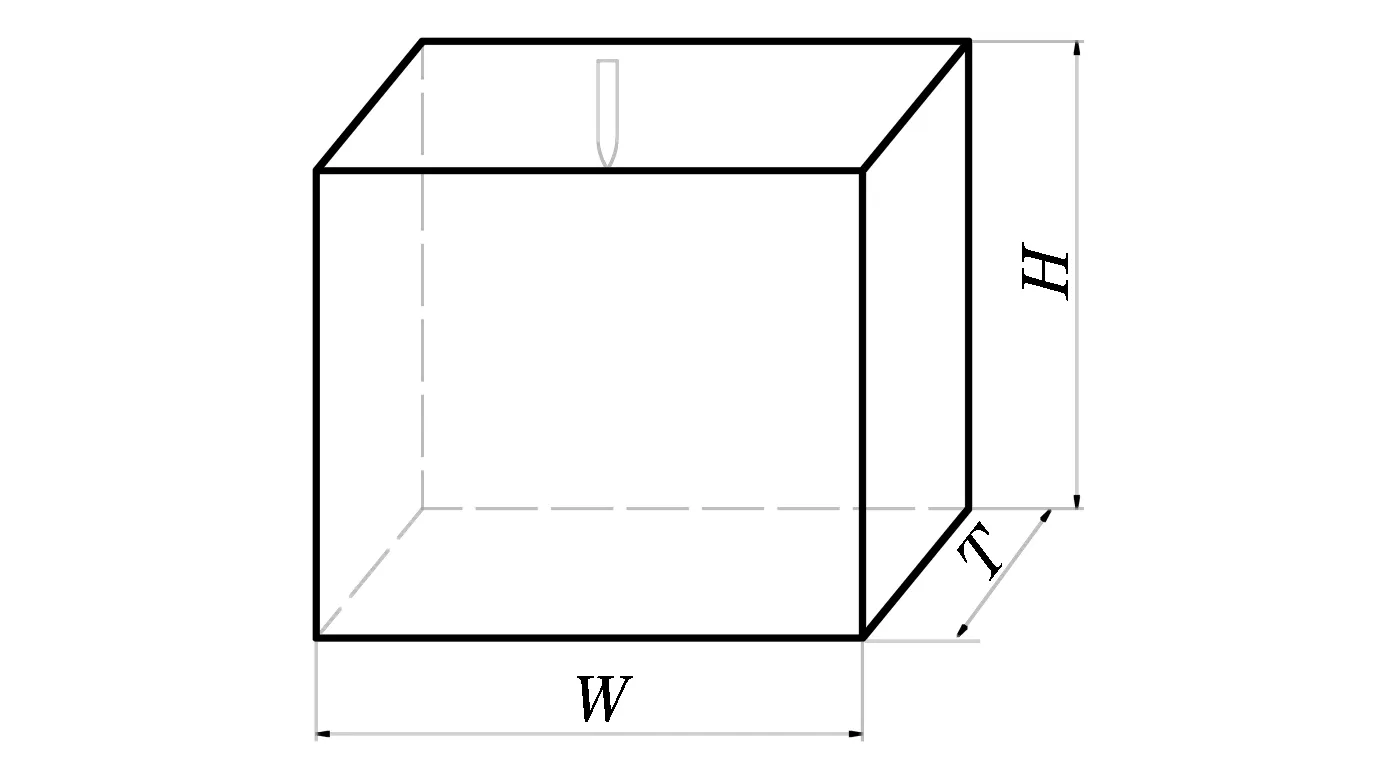
圖6 混凝土靶板尺寸Fig.6 Concrete target geometry

2.2 數值模擬靶板尺寸

彈體侵徹混凝土靶板時存在邊界效應。在彈速不超過800 m/s時，靶徑與彈徑之比約為30即可忽略側面邊界對侵徹過程的影響[16]。若對混凝土按均勻介質建模，該條件對于計算規模影響不大。但若基于細觀模型，滿足該條件則會導致計算量顯著增加，效率很低。本文重點在于討論彈體侵徹混凝土靶過程中的彈道偏轉規律，為提高計算效率，此處對比2種靶體尺寸的計算結果，分析采用較小尺寸的靶板是否滿足計算要求。

選擇S.J.Hanchak等[15]實驗中的彈體尺寸，見圖5，其直徑為25.4 mm。靶體尺寸布置如圖6所示，W、H、T分別為寬、高、厚。模型1的靶板尺寸為800 mm×600 mm×400 mm，靶徑與彈徑之比滿足大于30的要求；模型2的靶板在侵徹深度(H)方向保持高度不變，其余尺寸減小為模型1的一半，選為400 mm×600 mm×200 mm。模型參數與表2中一致。為了觀察彈體侵徹的彈道偏轉姿態，并減小計算規模，計算中采用1/2對稱模型，約束彈靶在垂直于對稱面方向上的位移及轉動自由度，其余邊界按無反射邊界處理。也即人工假定：若有彈道偏轉，僅發生在1/2對稱模型的對稱面上。

圖7給出了2種靶體尺寸有限元計算結果。從圖7可知，模型1和2得到的彈道軌跡偏轉現象較一致，而模型2的計算量更小，因此后續分析中將采用400 mm×600 mm×200mm的靶板尺寸。

圖7 不同尺寸的有限元模型彈道圖Fig.7 Ballistc trajectories of finite element models with different dimensions

3 剛性彈正侵徹偏轉影響因素分析

真實的彈體侵徹實驗，即使是在嚴格的正侵徹條件下，都可能存在彈道偏轉現象[10]。這里首先分別采用混凝土的均勻模型和細觀模型進行數值模擬，對比剛性彈正侵徹混凝土靶的侵徹過程。然后從混凝土細觀組成的角度分析彈道偏轉的影響因素。

3.1 計算模型

數值計算中，混凝土靶板尺寸均為400 mm×600 mm×200 mm(見圖6)，單元的基本尺寸為2 mm。彈體尺寸和形狀如圖5所示。細觀模型中骨料的體積分數為40%，骨料級配為二級配，也即小石(5～20 mm)與中石(20～40 mm)的體積比為5.5∶4.5。顯然，骨料尺寸與彈徑相當甚至大于彈徑，若骨料強度足夠大，則可以設想對彈體侵徹有重要作用。彈體入射位置為靶板中點，入射速度為800 m/s，根據文獻[17]可知，此時混凝土靶板侵徹過程中，可將彈體看作剛性彈。對彈體采用MAT_RIGID模型，對均勻模型中混凝土或細觀模型中骨料、砂漿及界面均采用K&C模型，參數見表2，邊界條件與2.2節中一致。

3.2 結果分析

3.2.1 現象分析

圖8～9分別給出了混凝土為均勻介質模型和細觀模型時，剛性彈以800 m/s的速度正侵徹靶板不同時刻的物理圖像，其中骨料和砂漿抗壓強度分別為160、15 MPa。從圖8～9可以看出，在800 m/s的入射速度下：均勻模型中彈體基本沒有發生偏轉，保持正侵徹狀態，此處由于顯式動力計算過程中輕微擾動導致混凝土中的應變非嚴格對稱；細觀模型中，由于骨料分布的隨機性，彈體在不同時刻出現不同程度的偏轉現象。以上現象表明，骨料、砂漿的力學特性的差異及隨機分布等因素對剛性彈體產生了不平衡力作用，導致侵徹方向變化，從正侵徹發展為斜侵徹。

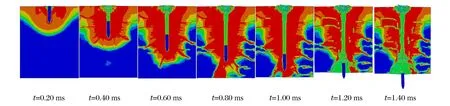
圖8 均勻模型混凝土靶的侵徹過程Fig.8 Penetration process of uniform concrete models

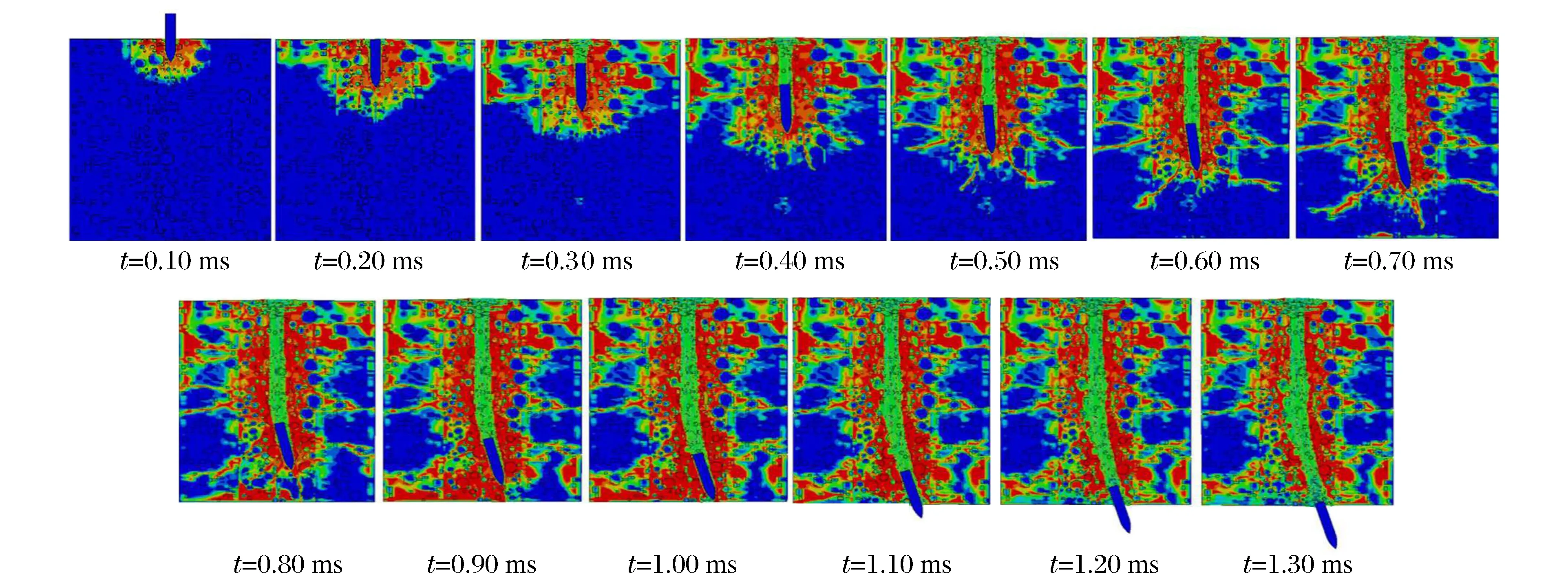
圖9 細觀建模的混凝土靶的侵徹過程Fig.9 Penetration process of mesoscopic concrete models

3.2.2 細觀模型中彈體運動過程分析

由剛體運動學可知，剛性彈體的運動可以視作彈體質心的平動和繞質心的轉動，如圖10所示。彈體的偏轉角度定義為彈體繞質心的轉動角度，則彈體侵徹過程中的位移及姿態可以用質心坐標(xC,yC)和繞質心的偏轉角度φ完全確定。選取對稱面中軸線上A、B兩個節點，兩者x方向坐標值之差為Δx，偏轉角度可以表示為φ=arcsin(Δx/L),L為彈體長度，如圖11所示。

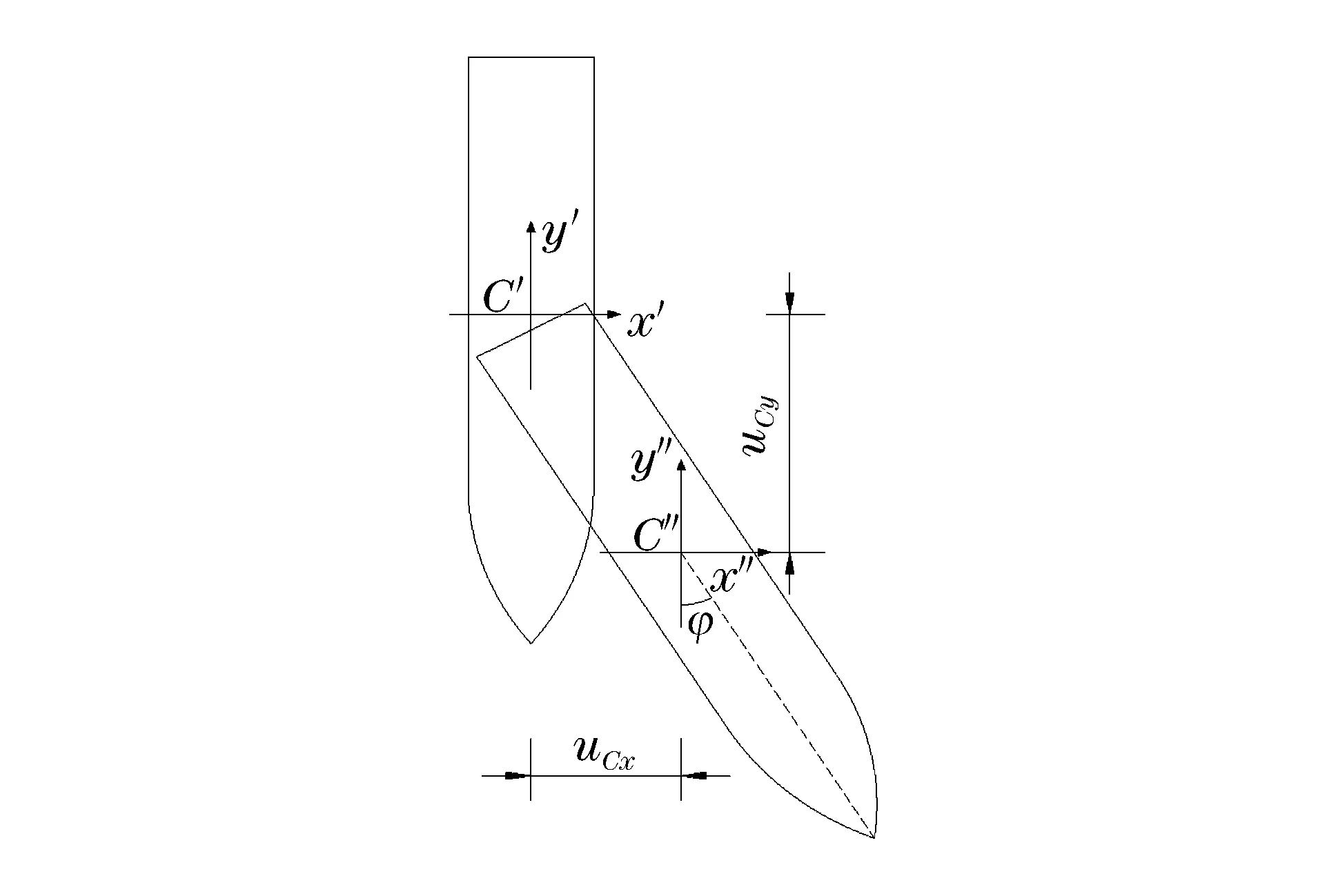
圖10 侵徹過程中剛性彈運動示意圖Fig.10 Motion of a rigid projectile during penetration

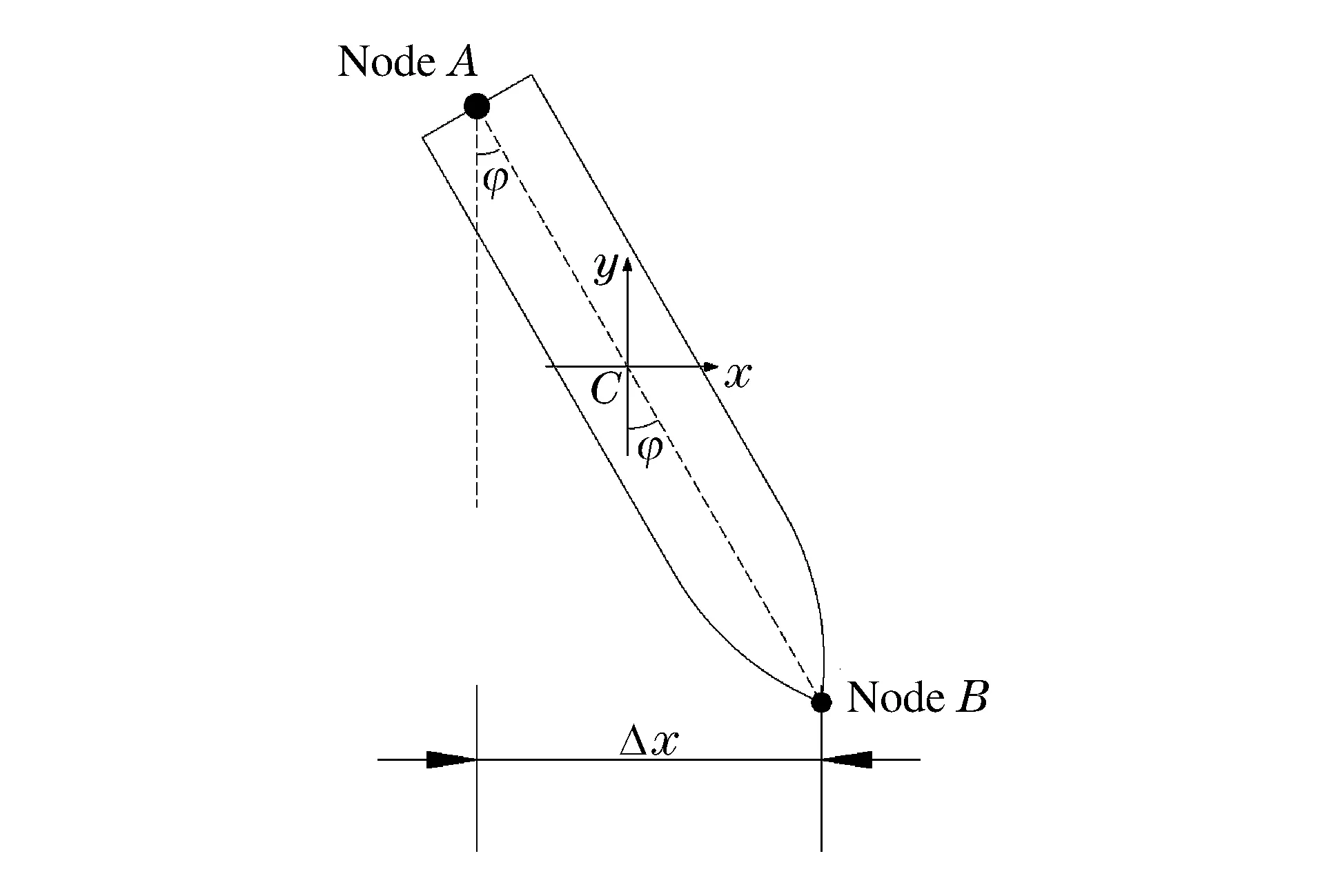
圖11 彈體偏轉角的定義Fig.11 Definition of the deflexion angle of a rigid projectile

為更清楚分析彈體在侵徹過程中的運動狀態，圖12給出了彈體質心水平加速度(aCx)、水平位移(uCx)及彈體偏轉角度(φ)隨時間的變化曲線,圖中正值表示方向為水平向左，負號表示方向為水平向右。由圖12(a)及圖9，可以看出，彈體侵徹過程大致可分為以下幾個時間段。

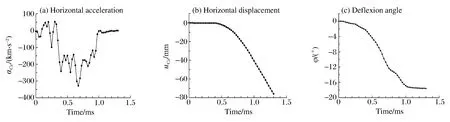
圖12 彈體侵徹過程中各參數隨時間的變化曲線Fig.12 Motion parameter-time curves of the projectile during penetration

(1)0～0.35 ms時間段內，彈體的水平加速度aCx在[-100，50] km/s2之間波動,如圖12(a)所示，混凝土靶體對彈體在垂直于侵徹方向上產生交替變換的橫向作用力；結合圖9，該時間段，靶體內骨料分布較均勻，彈體所受到的橫向加速度基本可以平衡，不足以使彈體質心產生橫向位移(圖12(b))，彈體的姿態幾乎不發生變化(圖12(c))；

(2)在0.35～0.40 ms時間段,從0.35 ms開始，彈體頭部左側連續碰撞到較大粒徑的骨料(圖9)，彈體向右側的加速度隨之增大(圖12(a))，導致彈體開始出現向右的橫向位移(圖12(b))，并產生偏轉現象(圖12(c))；

(3)在0.40～1.00 ms時間段，彈體在侵徹過程中，在慣性作用下，由于骨料等的連續碰撞，彈體所受橫向作用力保持穩定，彈體橫向位移和偏轉角度持續增加(圖12(b)～(c))；

(4)1.00 ms以后，彈體到達靶板背面并穿透靶板，不再承受橫向作用力，但彈體保持慣性仍有橫向位移，其偏轉角度保持恒定，直至出靶。最終彈體x方向位移為72.98 mm，偏轉角度為17.53°。彈體侵徹姿態發生較大的變化，從正侵徹轉變為帶攻角的斜侵徹。

陳小偉等[18]研究發現，無論剛性彈正/斜侵徹混凝土靶，若按均勻介質考慮，彈體進入隧道區后將始終保持正侵徹姿態；僅對于斜侵徹的開坑階段，由于不對稱的側向力作用，使得彈體承受繞質心的力矩作用，導致其運動姿態變化發生偏轉。而與此不同的是，考慮混凝土細觀建模后，即使剛性彈體正侵徹混凝土靶，在進入隧道區后，由于混凝土中多相材料性質的差異，導致彈體承受不對稱力作用，其運動姿態仍可能變化并發生偏轉(圖9)。

3.2.3 偏轉影響因素分析

通過上述侵徹過程的分析可知：剛性彈正侵徹混凝土靶過程中，彈體姿態的變化主要是由于混凝土中各相材料力學性能的差異引起彈體受到不對稱作用力而導致的。其中，骨料作為混凝土的骨架，其粒徑大小、位置分布等都對侵徹過程中彈體受力狀態存在較大影響。另一方面，侵徹過程中彈頭所受阻力可用空腔膨脹理論[19]進行分析，一般認為彈頭表面法向力不僅決定于靶材性質和侵徹速度，還受彈頭形狀影響，該阻力的橫向分量將導致彈體彈道偏轉。從彈體結構出發，彈體偏轉角度還與彈體長徑比相關。因此，基于混凝土細觀建模的彈體正侵徹混凝土細觀靶過程中，影響彈體偏轉的因素主要有混凝土各相材料(骨料、砂漿及界面等)力學性能(如強度、硬度、斷裂能等)、骨料幾何及位置分布、彈體初始撞擊速度、彈體頭部形狀和彈體長徑比等。

4 彈體彈道偏轉規律分析

針對前述影響彈體彈道偏轉的因素分析，本節中通過改變部分參數值進行數值模擬，分析這些參數對彈體彈道偏轉的影響規律。混凝土靶板尺寸、骨料級配及含量、彈體尺寸等均與3.1節中保持一致，彈體初始侵徹速度為800 m/s。仍采用1/2對稱模型和邊界約束。對混凝土中砂漿和骨料均采用K&C模型，對彈材取剛性模型，相關基本參數見表2。不同工況計算中，根據需要改變個別參數值。在考慮骨料隨機性影響時，則按同一靶體不同入射位置進行分析，即以模型對稱面中點為基點，按間距50 mm共取5個點為彈體入射位置，依次命名為L1、L2、C、R1及R2，如圖13所示。

4.1 骨料位置隨機分布對正侵徹彈體偏轉角度的影響

圖14給出了彈體在不同入射位置(可認為骨料分布隨機不同)正侵徹混凝土靶過程中偏轉角度的時程曲線。顯然，入射位置不同，彈體偏轉角度變化完全迥異。其一表現在最大偏轉角度值不同：當彈體從中點C位置侵入，最大偏轉角為11.70°；而彈體從L1位置侵入，最大偏轉角僅為1.10°，兩者相差約10倍。其二表現在偏轉角的正負(即左右)方向不同：彈體從不同位置侵入時，其偏轉角在左右方向上呈現一定波動，且偏轉方向可不同，如從位置L2侵入時，彈體向左邊偏轉，從位置R1侵入時，彈體向右偏轉。因此，可認為混凝土靶中骨料的隨機分布對彈體偏轉角度影響甚大。分析發現：由于靶體內骨料分布的隨機性導致彈體受力發生較大變化。在混凝土侵徹的數值模擬中，若采用均勻介質模型，有可能不足以全面反映彈靶侵徹/穿甲的真實物理過程。

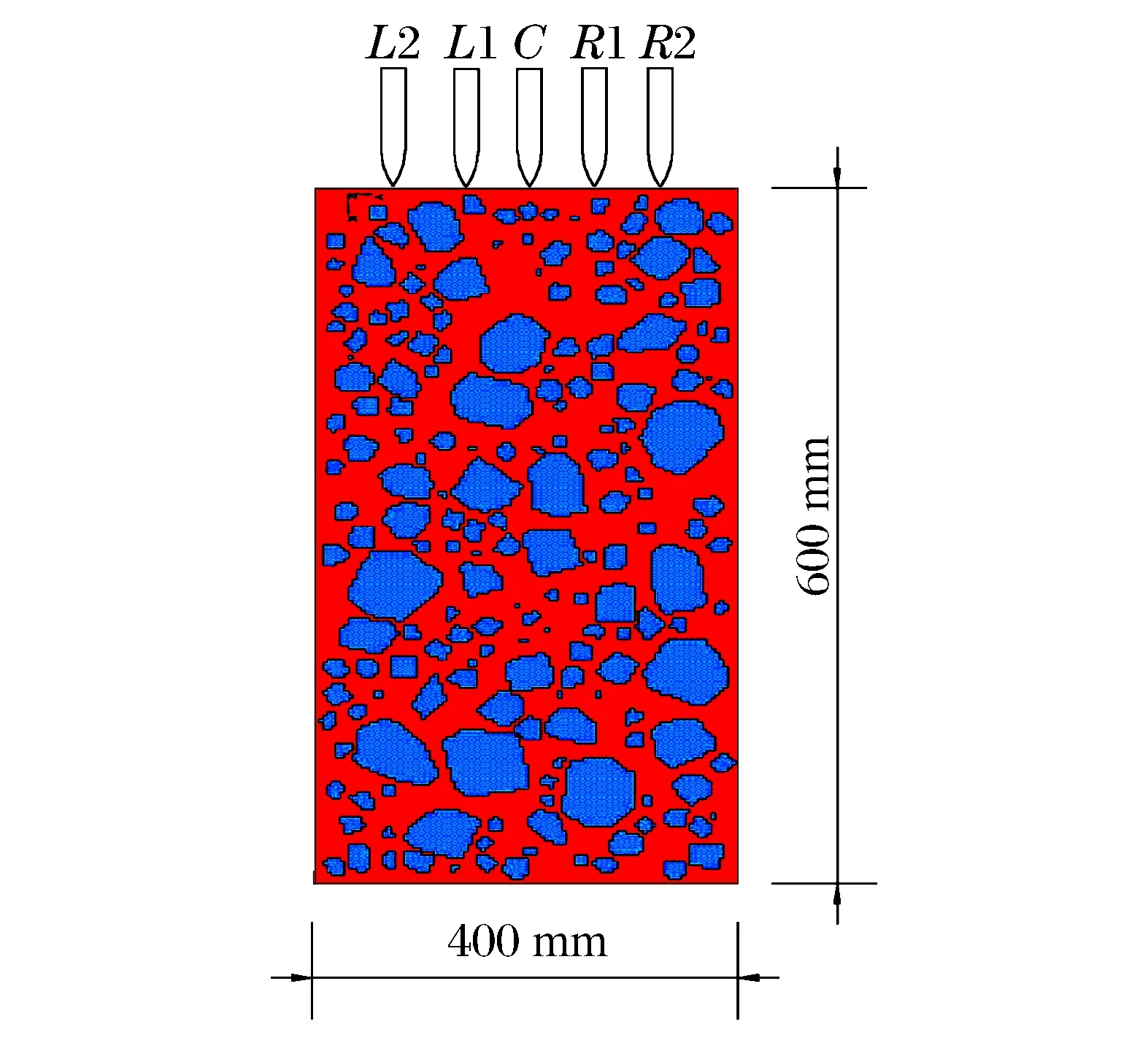
圖13 靶體尺寸及侵徹位置示意圖Fig.13 Target dimension and penetration location

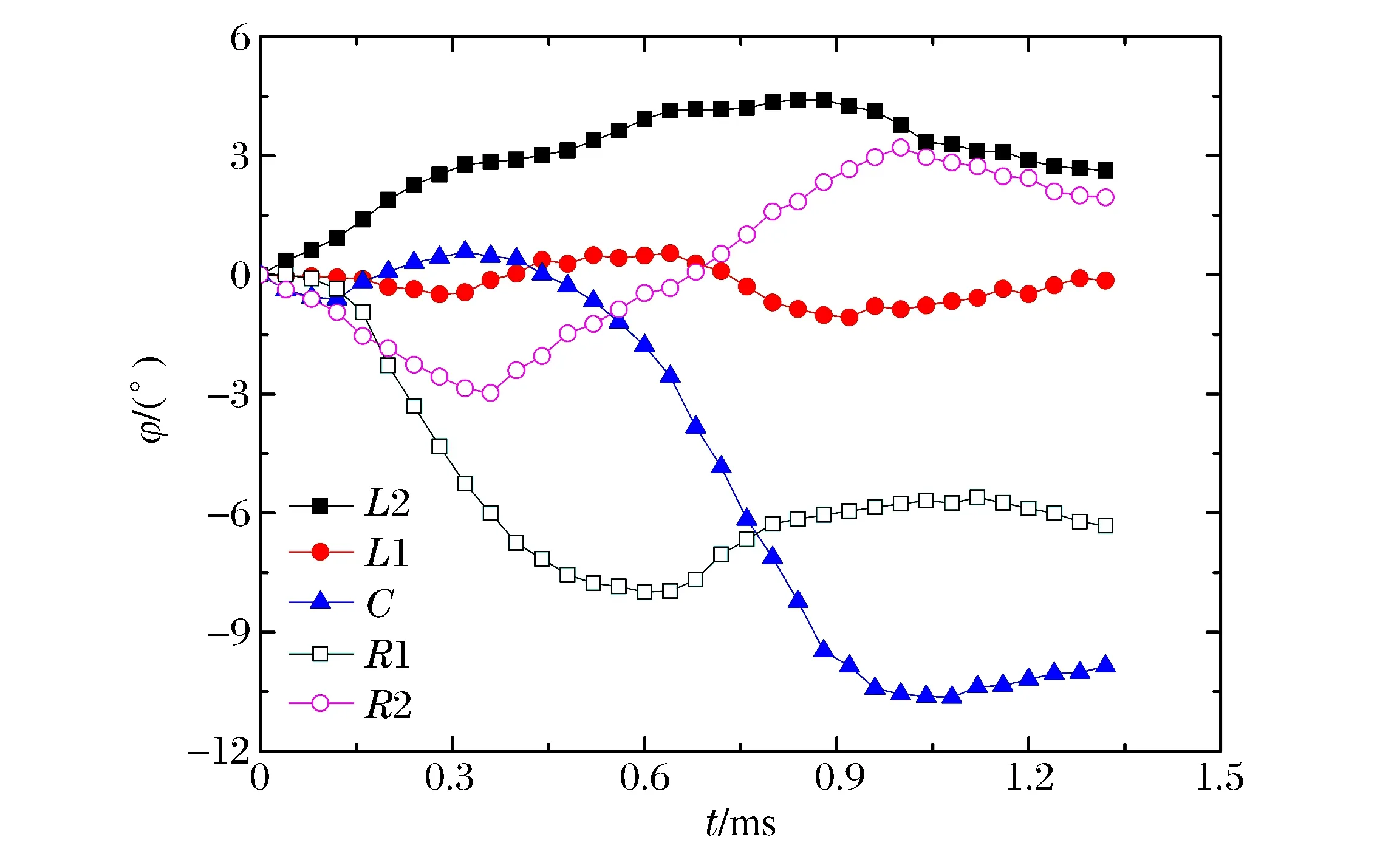
圖14 骨料隨機分布對彈體偏轉的影響 Fig.14 Projectile deflection affected by aggregate random distribution

4.2 骨料和砂漿的強度對正侵徹彈體偏轉角度的影響

圖15～16分別給出了彈體在骨料和砂漿不同強度的條件下正侵徹混凝土靶過程中偏轉角度的時程曲線。這里及以下僅給出在靶板中點C位置入射的結果分析，可認為從其余位置入射相應的參數影響規律一致。從圖15～16可以看出，不同骨料或砂漿強度下，同一位置侵入彈體的偏轉方向的變化規律基本一致。但彈體的最大偏轉角隨著骨料強度的增大而增大，特別地，當骨料強度從120 MPa增加到160 MPa時，偏轉角度最大值從1.89°增大到11.70°。這是由于骨料強度增大，加劇了其各相介質力學性能的差異，非均勻性表現更明顯，彈體受到骨料的非對稱力作用突然增大，導致偏轉角增大。顯著不同的是，如圖16所示，隨著砂漿強度的增大，彈體的偏轉角變小，當砂漿強度達到20 MPa時，可基本認為彈體無偏轉，這時砂漿與骨料的強度差減異小，混凝土材料趨于均勻。

一般地，砂漿強度小于骨料強度，當骨料強度增大時，骨料與砂漿強度的差異將顯著增大，這將增大混凝土不同相材料性能的差異并導致其隨機性增強。而骨料強度一定，僅增大砂漿強度，則使骨料與砂漿強度的差異減小，相反導致混凝土不同相材料的性能更均勻。對比可知：當骨料強度從60 MPa提高至160 MPa時，彈體偏轉角最大值從1.12°變為11.70°，增大約10.4倍；而砂漿強度從30 MPa降至5 MPa時，彈體偏轉角最大值從1.31°變為18.50°，增大約14倍。這說明砂漿強度的變化對彈體偏轉的影響較骨料強度的的變化對其的影響顯著。

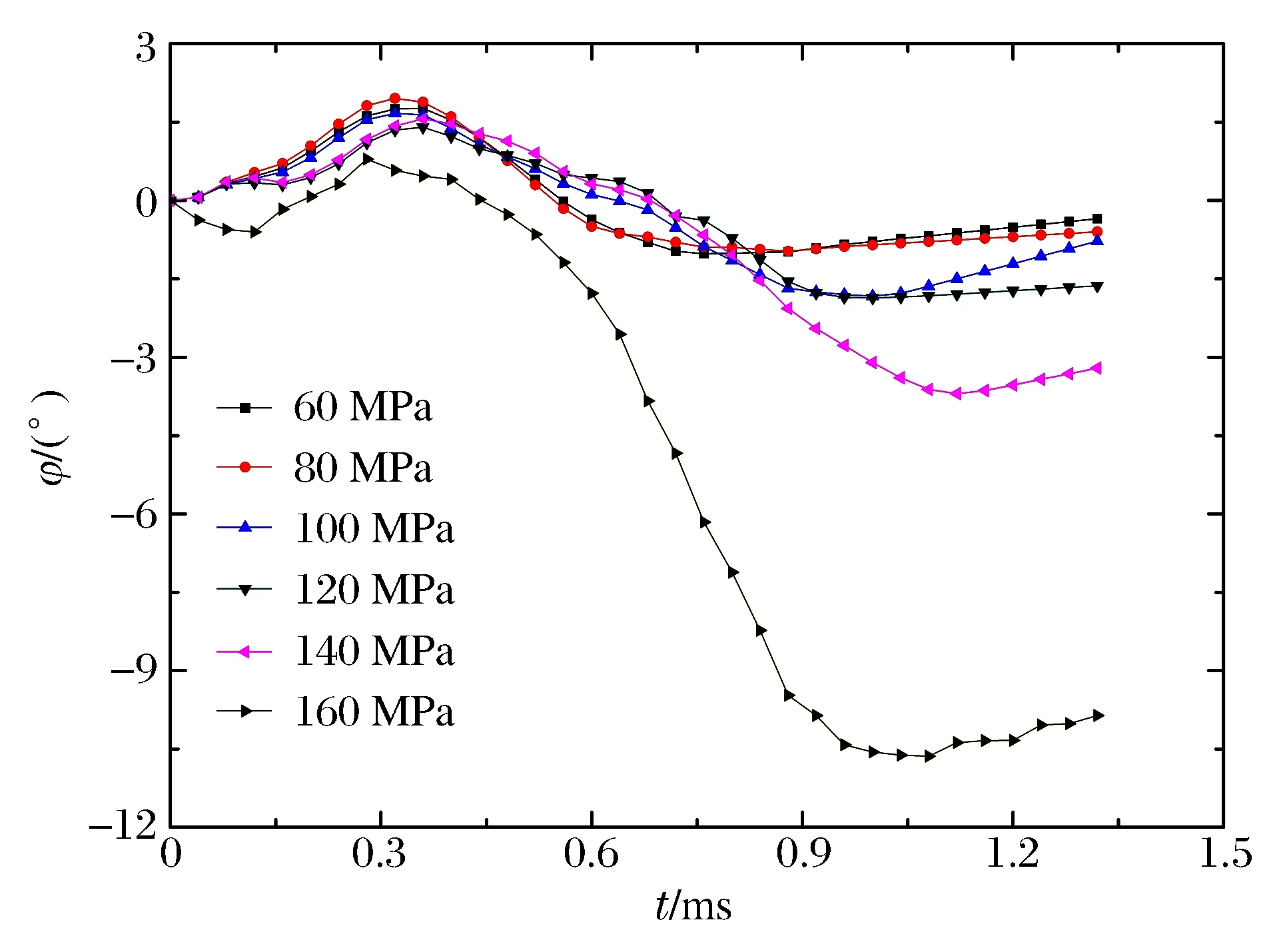
圖15 骨料強度對彈體偏轉的影響Fig.15 Projectile deflection affected by aggregate strength

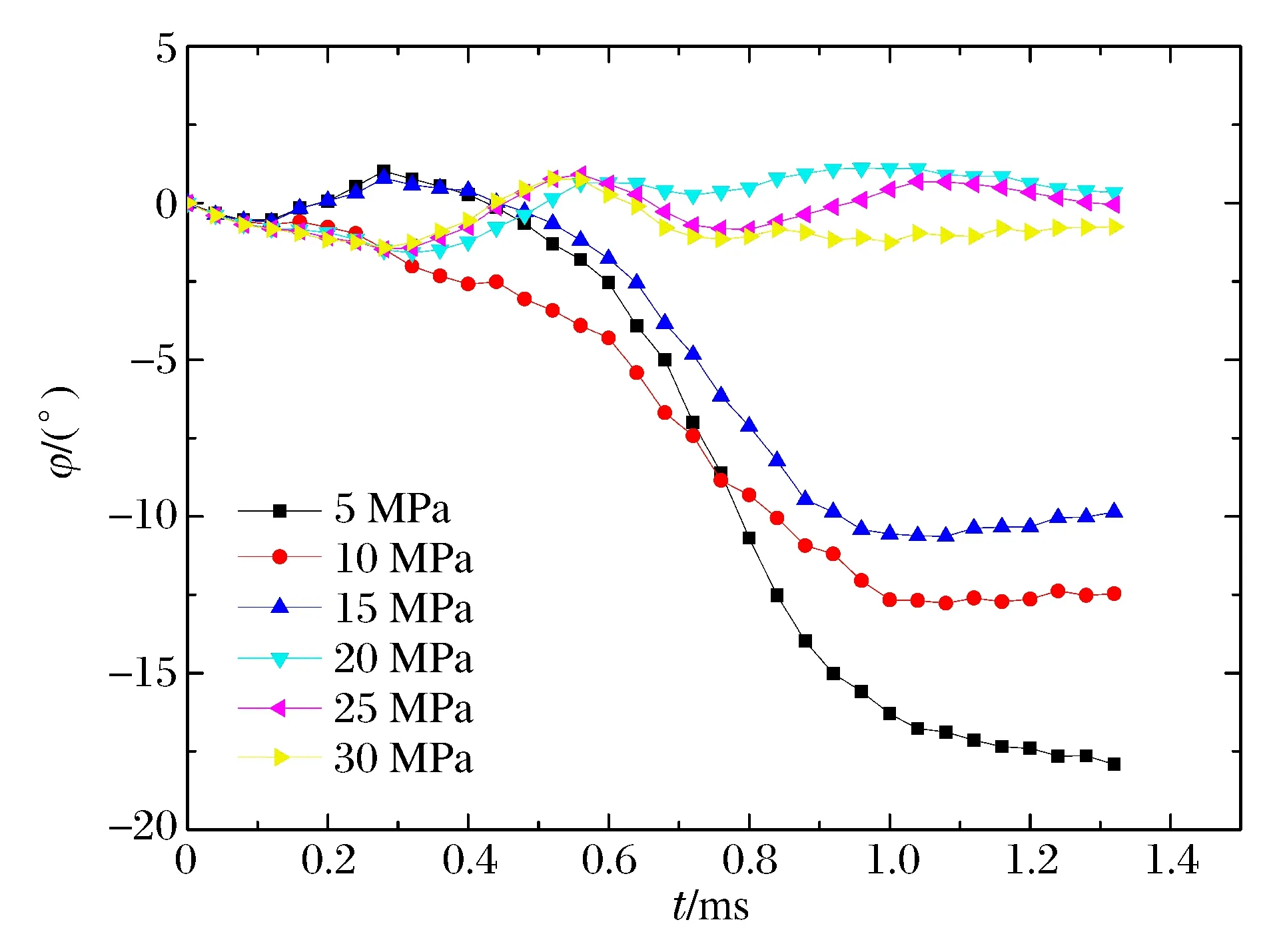
圖16 砂漿強度對彈體偏轉的影響Fig.16 Projectile deflection affected by motar strength

4.3 彈徑/骨料粒徑比和侵徹速度對正侵徹彈體偏轉角度的影響

為便于無量綱分析，在彈體其他條件一定情況下，定義彈徑/骨料粒徑比為γ=D/d，其中D為子彈直徑，d為骨料最大粒徑。計算中仍然采用圖5所示的彈形。為排除骨料隨機分布影響，這里僅通過改變彈體尺寸來實現不同的γ值，γ分別取0.40、0.85、1.67和2.67，則對應的最大骨料尺寸分別為65、30、15及10 mm。侵徹速度范圍為300～800 m/s，計算模型及相關的簡化原則均與3.1節中保持一致。圖17為不同入射速度下，不同γ值時，彈體偏轉角度的時程曲線,從圖17可以得出以下規律：

(1)同一侵徹速度下，彈體偏轉角度隨γ增大而逐漸減小；當γ增大到1.67時，偏轉角小于1.00°，可認為無偏轉。這是由于γ越大，則骨料越小，其他條件一致時，可認為混凝土各相材料趨于均勻。因此，在骨料強度一定時，當彈徑/骨料粒徑比達到一定值，可以不考慮混凝土細觀組成的影響，僅采用連續均勻介質進行模擬即可。

(2)同一γ值，當γ<1.67時，隨著侵徹速度增加，彈體偏轉角度有較大增長。其中γ=0.40，初始侵徹速度為800 m/s時偏轉角已經達到15.30°。當γ>1.67時，隨著初始侵徹速度的增大，偏轉角基本無變化，這與第1點相同。因此，將骨料的強度變化考慮進來，保守可認為在本文的計算條件下，若γ>2.00，即骨料最大尺寸為彈徑的1/2時，剛性彈正侵徹混凝土靶時不發生彈道偏轉，可將混凝土視作均勻介質。相反，若γ<2.00，彈道偏轉不可忽略，混凝土各相材料對侵徹影響較大，必須采用細觀模型才能正確描述彈體侵徹過程。

(3)彈體姿態在初始階段改變甚小，這與彈體正侵徹的實驗觀察相吻合。初始侵徹速度較小，彈體正侵徹過程中偏轉角幅值波動較大，這表明低速侵徹彈體的運動姿態容易受非對稱力作用而改變。當撞擊速度增高時，彈體偏轉角幅值在侵徹過程中單調增加，這是由于彈體具有更大運動慣性使然。

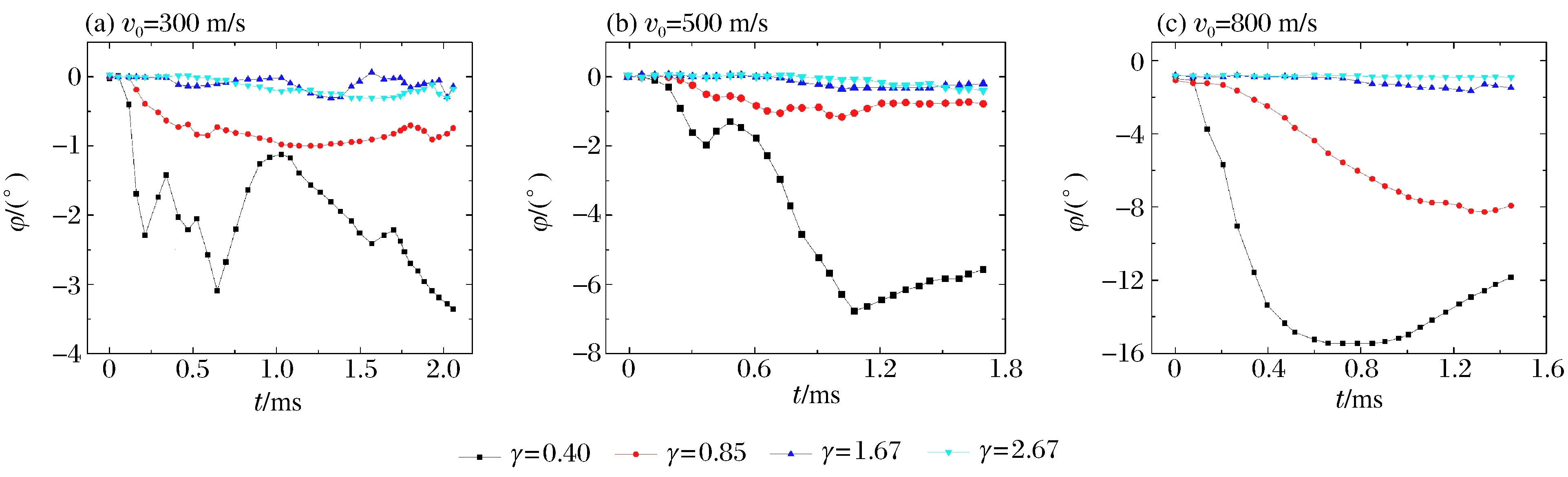
圖17 不同入射速度下，不同γ值時，彈體偏轉角度的時程曲線Fig.17 Deflection angle-time curves of the projectiles at different γ values and different impact velocities

5 結 論

基于混凝土骨料隨機投放的思想，建立了混凝土細觀數值模型，并進行了有效性驗證。以彈/靶正侵徹實驗為基礎，分析了剛性彈侵徹混凝土細觀模型的侵徹過程，探討了混凝土細觀參數對彈體偏轉的影響。得到如下結論：

(1)與均勻模型模擬不同的是，用混凝土細觀模型模擬剛性彈正侵徹時，在侵徹隧道區可能發生彈體彈道偏轉。也即，混凝土細觀數值模型可以較好反映彈體正侵徹過程中彈道偏轉等典型物理現象。

(2)混凝土細觀參數對于彈體彈道偏轉有顯著影響。隨著骨料強度的降低及砂漿強度的增大，彈體偏轉角度有所降低，且砂漿強度變化對于彈道偏轉影響較骨料強度變化大。

(3)考慮剛性彈正侵徹的彈道偏轉時，存在一個彈體直徑/骨料最大粒徑比的特征比值。也即，當彈徑足夠大時，混凝土細觀組成對于彈道偏轉影響可以忽略，可將混凝土當作均勻介質處理；反之，骨料足夠大，則應采用細觀模型進行數值模擬。

[1] Backmann M E, Goldsmith W. The mechanics of penetration of projectiles into targets[J]. International Journal of Engineering Science, 1978,16(1):1-99.

[2] 錢偉長.穿甲力學[M].北京:國防工業出版社,1984:23-35.

[3] Goldsmith W. Review: Non-ideal projectile impact on targets[J]. International Journal of Impact Engineering, 1999,22(2/3):95-395.

[4] Corbett G G, Reid S R, Johnson W. Impact loading of plates and shells by free-flying projectiles: A review[J]. International Journal of Impact Engineering, 1996,18(2):141-230.

[5] Li Q M, Reid S R, Wen H M, et al. Local impact effects of hard missiles on concrete targets[J]. International Journal of Impact Engineering, 2006,32(1/2/3/4):224-284.

[6] Warren T L, Fossum A F, Frew D J. Penetration into low-strength (23 MPa) concrete: Target characterization and simulations[J]. International Journal of Impact Engineering, 2004,30(5):477-503.

[7] Forrestal M J, Frew D J, Hickerson J P, et al. Penetration of concrete targets with deceleration-time measurements[J]. International Journal of Impact Engineering, 2003,28(5):479-497.

[8] 陳小偉.穿甲/侵徹問題的若干工程研究進展[J].力學進展,2009,39(3):316-351. Chen Xiaowei. Advances in the penetration/perforation of rigid projectiles[J]. Advances in Mechanics, 2009,39(3):316-351.

[9] Neville A M. Properties of concrete[M]. 5ed. Prentice Hall, 2012:112-119.

[10] 何翔,徐翔云,孫桂娟,等.彈體高速侵徹混凝土的效應實驗[J].爆炸與沖擊,2010,30(1):1-6. He Xiang, Xu Xiangyun, Sun Guijuan, et al. Experimental investigation on projectiles’ high-velocity penetration into concrete target[J]. Explosion and Shock Waves, 2010,30(1):1-6.

[11] Wang Z M, Kwan A K H, Chan H C. Mesoscopic study of concrete I: Generation of random aggregate structure and finite element mesh[J]. Computers and Structures, 1999,70(5):533-544.

[12] Fuller W B, Thompson S E. The laws of proportioning concrete[M]∥The American Society of Civil Engineers. Transactions of the American Society of Civil Engineers: Vol.LIX, 1926:67-172.

[13] 劉光廷,高政國.三維凸型混凝土骨料隨機投放算法[J].清華大學學報(自然科學版),2003,43(8):1120-1123. Liu Guangting, Gao Zhengguo.Random 3-D aggregate structure for concrete[J]. Journal of Tsinghua University (Science and Technology), 2003,43(8):1120-1123.

[14] Vervuurt A. Interface fracture in concrete[D]. Delft University of Technology, 1997:45-49.

[15] Hanchak S J, Forrestal M J. Perforation of concrete slabs with 48 MPa (7 ksi) and 140 MPa (20 ksi) unconfined compressive strengths[J]. International Journal of Impact Engineering, 1992,12(1):1-7.

[16] 梁斌.彈丸對有界混凝土靶侵徹研究[D].綿陽:中國工程物理研究院,2004:62-89.

[17] 陳小偉,李繼承.剛性彈侵徹深度和阻力的比較分析[J].爆炸與沖擊,2009,29(6):584-589. Chen Xiaowei, Li Jicheng. Analysis on the penetration depth and resistive force in the deep penetration of a rigid projectile[J]. Explosion and Shock Waves, 2009,29(6):584-589.

[18] Chen Xiaowei. Dynamics of metallic and reinforced concrete targets subjected to projectile impact[D]. Singapore: Nanyang Technological University, 2003:50-67.

[19] 李志康,黃風雷.混凝土材料的動態空腔膨脹理論[J].爆炸與沖擊,2009,29(1):95-100. Li Zhikang, Huang Fenglei. dynamic spherical cavity-expansion theory for concrete materials[J]. Explosion and Shock Waves, 2009,29(6):95-100.

(責任編輯 張凌云)

On ballistic trajectory of rigid projectile normal penetration based on a meso-scopic concrete model

Deng Yongjun1,2, Chen Xiaowei1,2, Yao Yong1, Yang Tao1

(1.SchoolofCivilEngineeringandArchitecture,SouthwestUniversityofScienceandTechnology,Mianyang621000,Sichuan,China;2.InstituteofSystemsEngineering,ChinaAcademyofEngineeringPhysics,Mianyang621999,Sichuan,China)

To study the effect of the concrete’s mesoscopic factors on the deflection of the rigid projectile’s ballistic trajectory, we established a 3-D mesoscopic model for the concrete based on the idea of randomly distributed aggregates, analyzed the causes and possible contributing factors of the ballistic trajectory deflection of the rigid projectile penetrating into a concrete target, and examined quantitatively the influence of the mesoscopic factors of the concrete. The results show that the mesoscopic concrete model is able to reflect the typical physical phenomena of a projectile’s normal penetration, that the mesoscopic factors have significant effect on the deflection of the ballistic trajectory as the rigid projectile is penetrating into the mesoscopic concrete, and that there exists a characteristic ratio of the projectile’s diameter to the largest possible diameter of the aggregate.

concrete; meso-scopic model; rigid projectile; normal penetration; ballistic trajectory deflexion

10.11883/1001-1455(2017)03-0377-10

2015-10-09；

2016-03-27

國家自然科學基金項目(11225213,11390361,11390362);中國工程物理研究院重點學科項目

鄧勇軍(1987— ),男,博士研究生,助理研究員; 通信作者: 陳小偉,chenxiaoweintu@yahoo.com。

O382 國標學科代碼： 13035

A