基于多軸應力損傷的薄板花瓣型破口形成機理研究*

李 營,吳衛國,張 磊,杜志鵬,張 瑋,趙鵬鐸

(1.武漢理工大學交通學院,湖北 武漢 430063;2.海軍裝備研究院,北京 100161)

基于多軸應力損傷的薄板花瓣型破口形成機理研究*

李 營1,2,吳衛國1,張 磊2,杜志鵬2,張 瑋2,趙鵬鐸2

(1.武漢理工大學交通學院,湖北 武漢 430063;2.海軍裝備研究院,北京 100161)

開展了多種應力狀態下的船用鋼力學特性實驗，基于多軸應力狀態損傷的失效準則研究了局部沖擊荷載作用下圓形板的花瓣型破口形成過程，劃分了花瓣型破口形成的3個階段，分析了裂紋區域、非裂紋區域應力狀態變化過程及損傷情況。得到:(1)考慮多軸應力損傷的艦船用鋼失效準則能有效預測受力狀態復雜的花瓣狀破口；(2)花瓣型破口的形成主要分為蝶形凹陷、中心區域裂紋擴展、花瓣形成與翻轉等3個階段；(3)花瓣型破口的裂紋區和非裂紋區均受力復雜，破口預測須考慮應力狀態對損傷特性的影響；(4)花瓣形成過程中，第1階段和第3階段均勻變形，第2階段損傷局部化明顯，花瓣卷曲會造成花瓣根部的二次損傷。

花瓣型破口；應力三軸度；應力狀態；失效準則

水面艦艇結構在戰時易遭受魚雷、水雷和反艦導彈的攻擊，造成艦艇結構破損甚至斷裂。由于爆炸實驗耗費巨大的財力、物力，數值仿真成為有效的輔助手段。數值仿真效果取決于兩個方面，即精確的算法和良好的材料性能表征。而數值模擬所產生的誤差中，材料表征帶來的誤差遠大于計算程序數值求解帶來的誤差[1]。準確的材料斷裂表征參數是開展爆炸作用下艦船結構毀傷模式預測與評估的重要前提。花瓣型破口是爆炸作用下板架結構的重要破壞模式之一[2]。對花瓣性破口的數值模擬和理論分析一般基于單向應變假設和雙向應變假設[3]，設定斷裂應變為某一具體塑性應變值。但基于板架爆炸實驗的終點效應，反推破口處等效塑性應變值的方法有一定的誤差，且不同實驗給出的結果差異較大，給參數的選擇帶來一定的困難：牟金磊等[3]開展水下爆炸實驗，分析了破口裂紋處的厚度變化，提出采用0.388作為失效應變判據；陳長海等[4]則根據空中接觸爆炸的實驗結果提出斷裂應變的極限值為0.605，在數值模擬中采用了塑性應變0.28作為斷裂應變[5]。爆炸作用下金屬材料的失效與應力狀態密切相關[6]：在單向拉伸到雙向拉伸過渡區域，金屬材料斷裂應變呈指數遞減[7]；在多向受壓應力狀態下，金屬材料甚至完全不會失效[8]。在爆炸荷載作用下，花瓣型破口是否為簡單的單向拉伸或者雙向拉伸，應力狀態又如何影響損傷斷裂過程，值得深入研究。本文中，分析不同應力狀態下船用鋼的斷裂應變，基于多軸應力損傷的ABAQUS子材料斷裂準則模型對局部沖擊作用下花瓣型破口的形成過程進行計算，分析斷裂區、非斷裂區的應力狀態變化，局部損傷特性等，論證花瓣型破壞模式下應力狀態變化對準確預測破壞程度和破口大小的重要性。

1 船用鋼斷裂特性

1.1 材料實驗

船用鋼較一般結構鋼強度高、韌性強，對爆炸沖擊等載荷具有更強的抗力。單軸受拉應力狀態下船用鋼的失效特性由拉伸實驗獲得。試件參照《GB/T228-2002》[9]制作。試件為板狀，厚2.7 mm，設計實驗段長度為40 mm。在常溫20 ℃的環境下，使用微機控制萬能材料試驗機(INTRON5882)以5 mm/min的拉伸速度進行準靜態拉伸實驗。通過迭代有限元參數輸入的方法對比力-位移曲線，不斷校正應力應變關系。拉伸試樣力-位移曲線如圖1所示。

如圖2所示，設計純剪切試樣的單向拉伸實驗實現剪切應力狀態,試樣厚度分別為2.7和4.7 mm。與缺口圓棒拉伸實驗不同，剪切件在斷裂時的等效塑性應變難以通過理論公式確定。以中間斷面為研究對象進行了有限元迭代校正，直到數值模擬與實驗的力-位移曲線十分接近為止，通過多次修正，有限元計算結果與實驗結果較一致。

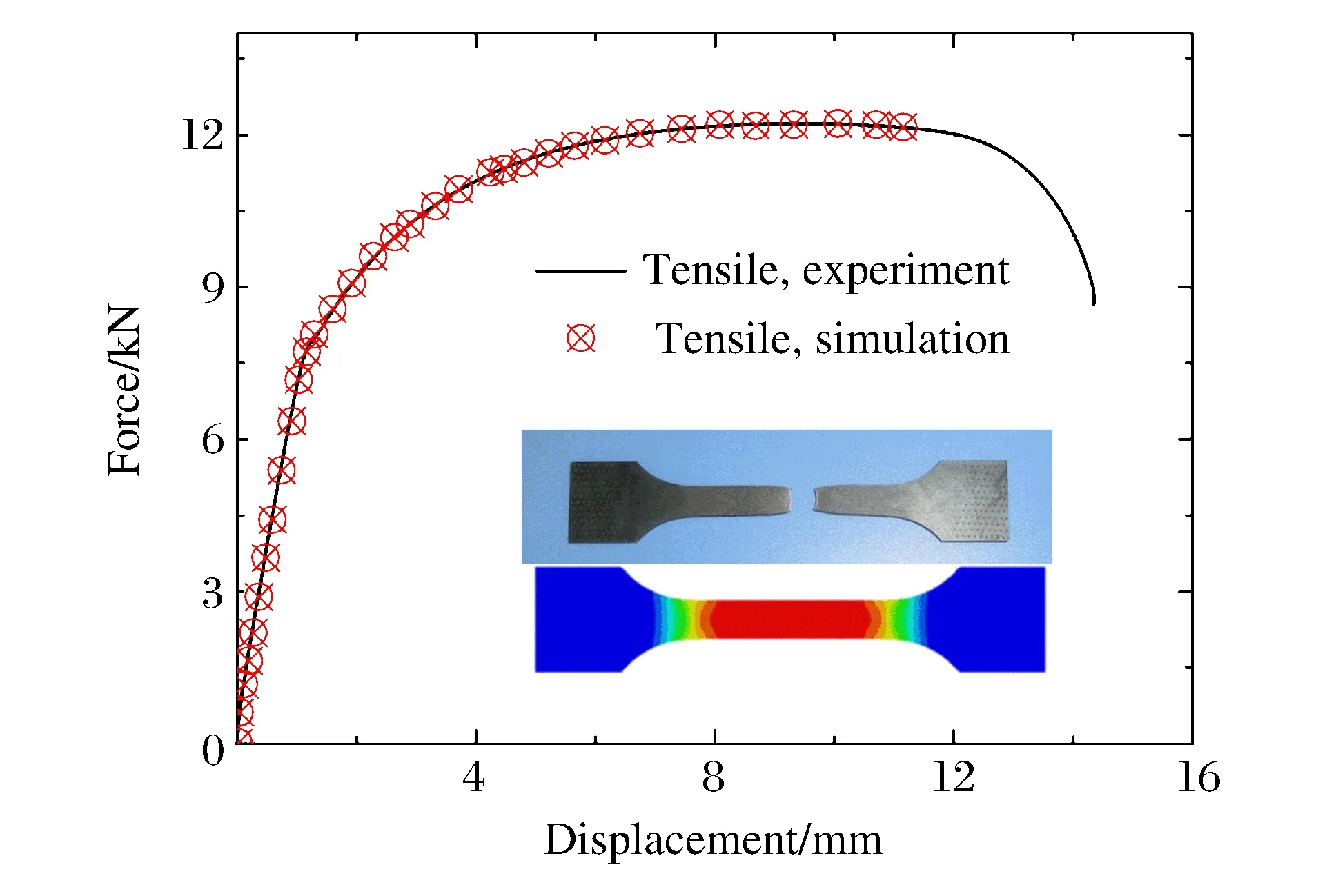
圖1 拉伸試樣及力-位移曲線Fig.1 Tensile specimen and its force-displacement curves

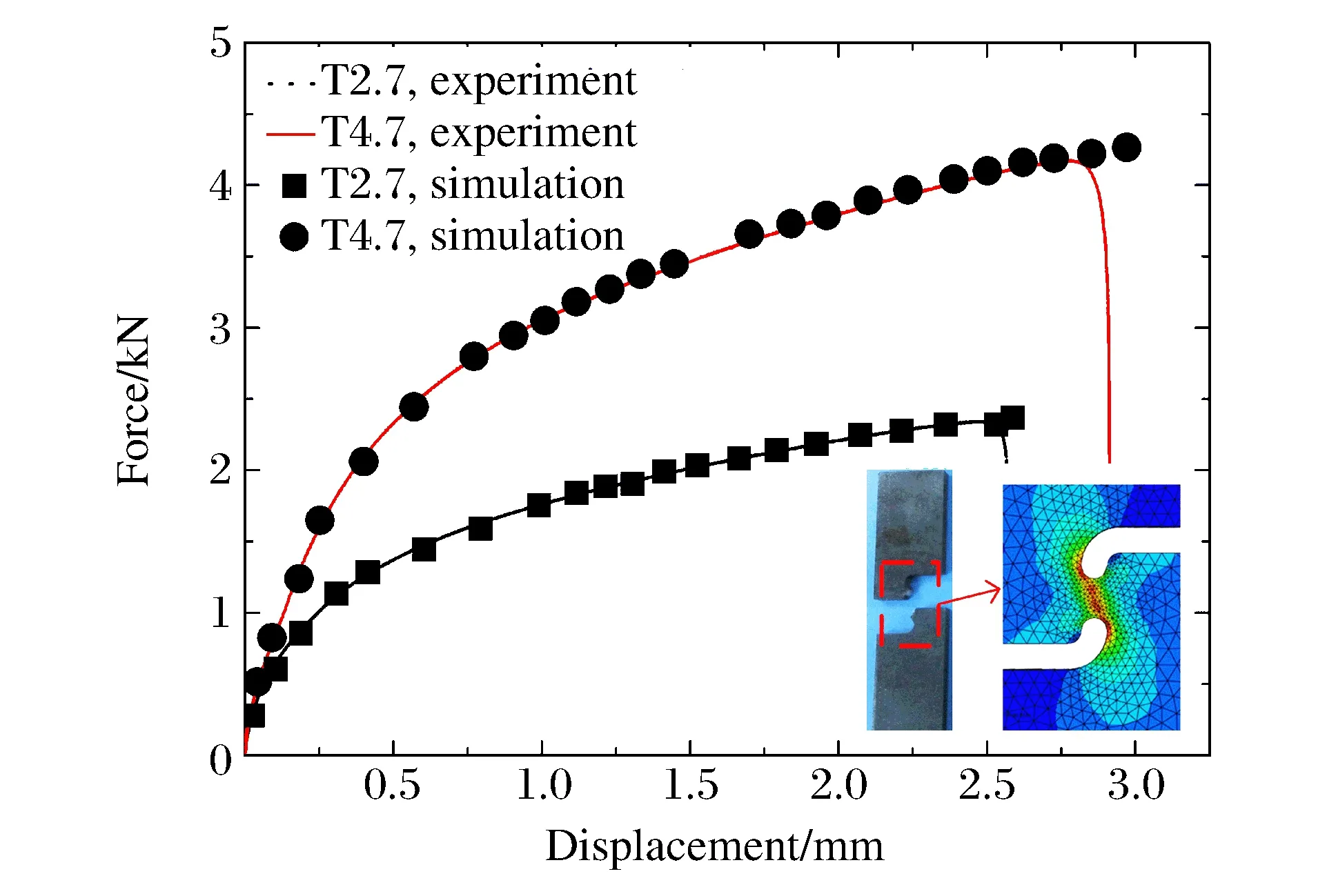
圖2 剪切試樣及力-位移曲線Fig.2 Shear specimen and its force-displacement curves

1.2 斷裂準則

對不同應力狀態下的船用鋼實驗結果采用下式[10]：

(1)

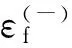
為計算變形過程中的損傷，定義單元的損傷為:

D=Δεp/εf

(2)

式中：D為損傷參數，D=0～1，初始時D=0，當D=1時材料失效； Δεp為一個時間步的塑性應變增量，εf為當前時間步斷裂應變。

不同斷裂準則對斷裂應變值的預測結果如表2所示,εf,exp為斷裂應變實驗值。可以看出，采用新斷裂準則的預測結果εf,new明顯好于采用常用等效塑性應變準則的預測結果εf,nom。

表1 不同準則預測的斷裂應變值

2 局部沖擊載荷下的花瓣型破口

2.1 花瓣狀破口的形成過程

采用ABAQUS建模計算，建立直徑為600 mm的圓形薄板，設置為板單元，厚度為3 mm，四周邊界固定約束。中心直徑為50 mm的核心區域通過施加初速度(100 m/s)的方式加載局部沖擊載荷。

圖3為花瓣型破口形成過程的俯視和側視圖。由圖3可以看出，整個花瓣變形分為3個階段：(1)蝶形凹陷階段,如圖3(a)～(b)所示,中間局部區域受沖擊載荷作用出現局部凹陷，在中心運動區域與未運動區的過渡區域，由于速度梯度較大，易發生較大的塑性變形，整體呈現凸臺狀，出現局部頸縮，甚至整個中心運動區域飛出，形成充塞破口;(2)中心區域裂紋擴展階段，如圖3(c)～(d)所示，在蝶形凹陷區邊界與中心處，由于變形梯度較大，形成若干裂紋，在局部結構繼續運動的情況下，主裂紋長度持續增大，并發生擴展，中心區域出現局部碎裂破片；(3)花瓣形成與翻轉階段，如圖3(e)～(f)所示，中心區域碎片繼續飛出，裂紋此時不再擴展，花瓣因后續慣性與徑向拉力聯合作用向后翻轉，發生較大塑性變形，花瓣最終形成。

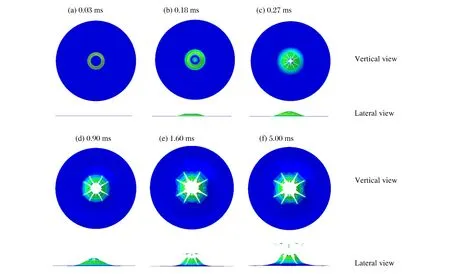
圖3 花瓣型破口形成過程Fig.3 Petaling formation process

2.2 典型區域應力狀態

圖4為裂紋擴展區域不同位置失效單元的應力三軸度變化曲線。3個不同測點距離圓心80、52和33 mm，分別位于花瓣間裂紋區、蝶形凹陷過渡區及中心運動區域內。3個測點位置的單元均先受拉伸作用，接著過渡到拉剪、剪切和壓縮區，并依次發生損傷。從應力三軸度的變化可以看出，整個花瓣變形過程中，各失效單元的受力狀態發生較大變化，單一的雙向受拉無法準確描述。

圖5為非碎裂區不同位置處應力三軸度變化曲線。花瓣區、圓板邊緣及中間過渡區受力狀態有明顯差異：(1)花瓣區(element at petal)最早受到拉伸作用，應力三軸度約為0.6，屬于雙向拉伸，接著花瓣裂紋擴展形成自由界面，拉伸波轉換成壓縮波，局部受力由雙向拉伸轉換成雙向壓縮，接著由于花瓣頂部位置翻卷，花瓣中的單元受到較持續的拉伸作用；(2)接近邊緣處的測點(element at edge)則在作用開始時間上滯后于花瓣和過渡區，受到一段持續時間較長的拉伸作用，后續也會進入交替的拉伸和壓縮作用，偶有剪切應力狀態，但整體上看，后期(2.4 ms以后)主要受拉伸作用；(3)花瓣和邊界的過度區內(element between edge and petal)，測點受拉伸作用的起始時間介于花瓣和邊緣之間，起初受到較長時間雙向拉伸波的作用，接著由于反射波的作用測點承受剪切甚至壓縮作用的交替作用，稍后由于花瓣的向外翻轉，測點將承受較長時間的拉伸作用。

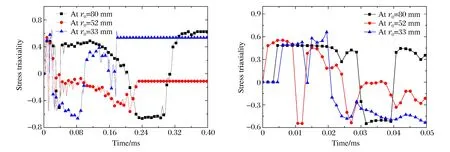
圖4 裂紋擴展區失效單元的應力三軸度Fig.4 Stress triaxiality of failure elements at crack

圖5 非裂紋區單元的應力三軸度Fig.5 Stress triaxiality of elements out of crack

2.3 局部損傷程度

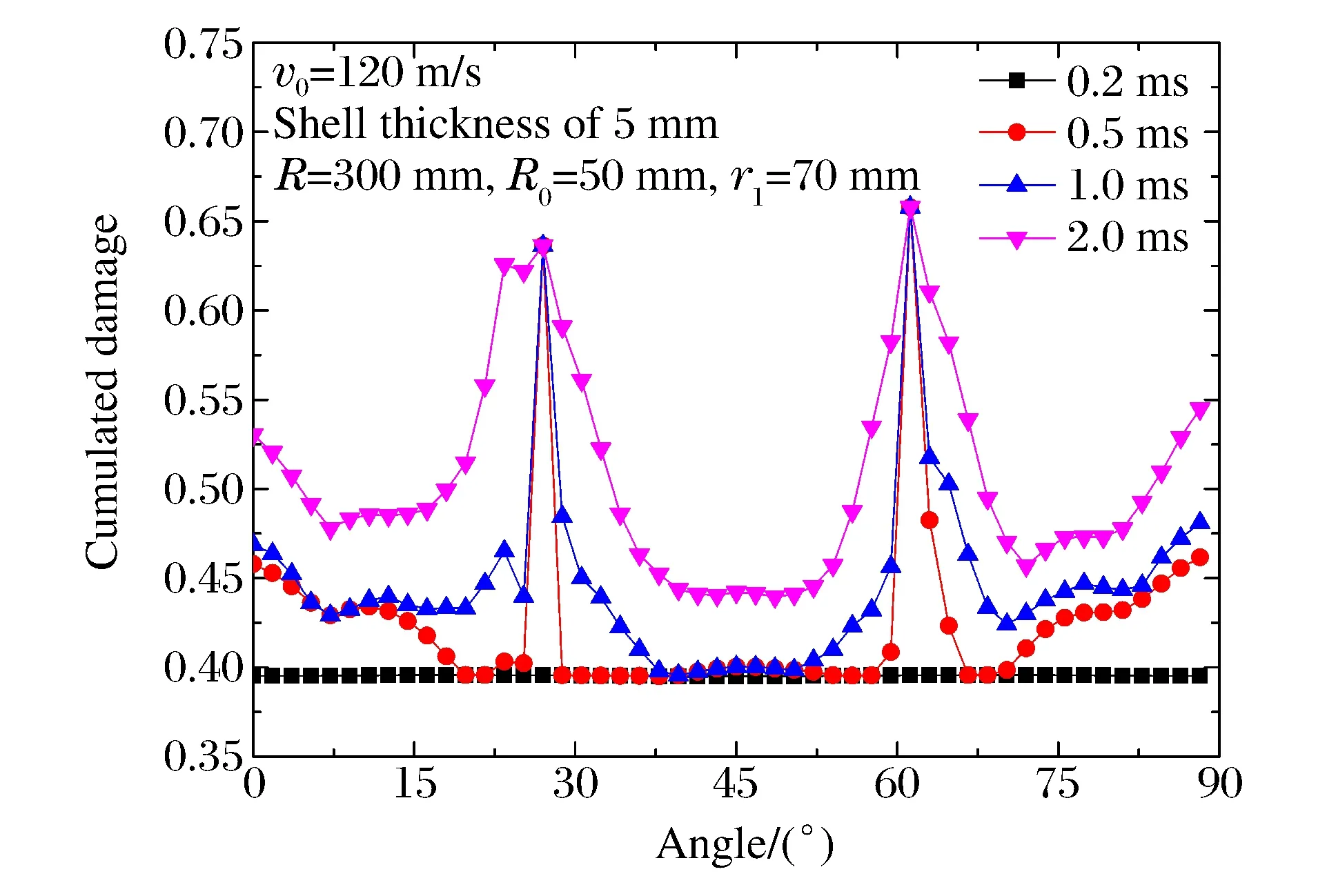
圖6 裂紋區環向單元累積損傷Fig.6 Cumulated damage of elements at crack

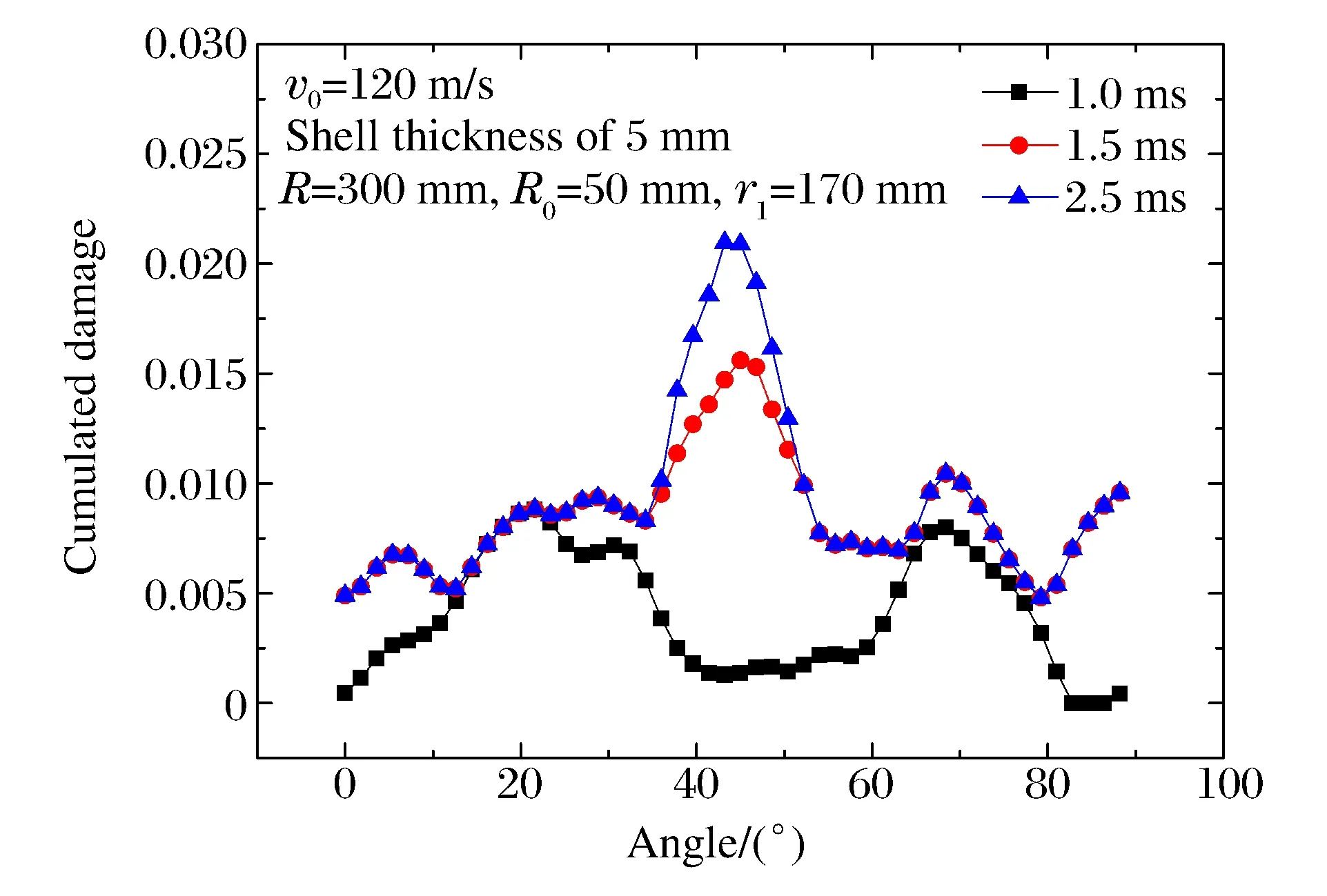
圖7 非裂紋區環向單元累積損傷Fig.7 Cumulated damage of elements out of crack

圖6為距中心70 mm處的累積損傷情況(0°～90°范圍內),圖中R為圓板直徑，R0為加載區域半徑。與2.1節對應，各曲線從時間和物理階段的不同劃分為3個階段，分別為：(1)蝶形凹陷造成的均勻加載，各測點損傷較一致，均小于0.4(0.2 ms時的曲線)；(2)裂紋迅速擴展形成(0.5 ms)時，28°與62°處的損傷迅速發展，形成2個“山峰”，并遠大于周圍值；1.0 ms時，峰值附近的值有一定的塑性累積，損傷度稍有增大；(3)花瓣翻轉造成的均勻損傷，該階段特征為，除“山峰”外，其他各處的損傷程度均有一定程度的增大，且幅值基本相當(2.0 ms時的曲線)。

圖7為距中心170 mm處的累積損傷情況(0°～90°)。不同區域的損傷發展先后不同，首先為28°與62°處裂紋前端產生明顯損傷(1.0 ms)，其他區域發展不明顯；1.0 ms后，裂紋前端區發展不明顯，2個裂紋中間由于花瓣的彎曲，形成一定的塑性損傷區。說明花瓣卷曲會造成花瓣根部的二次損傷。

3 探 討

由上述分析可以看出，爆炸等局部沖擊作用下，薄花瓣型破口形成過程受力狀態復雜，遠非雙向受拉所能描述。圖8為薄板爆炸后形成的花瓣與碎裂與文獻[4,12]實驗結果比對的情況。可以看出，考慮應力狀態的斷裂準則對于準確預測花瓣的形成，以及爆炸碎片的預測和描述較適用。傳統的等效塑性應變準則，將失效參數設置為一常數，不考慮應力狀態的影響，難以描述復雜應力狀態下板的破壞機理。考慮應力狀態對金屬材料影響的失效準則，才能揭示花瓣型破口形成機理，更有效地預測復雜應力狀態下的薄板失效模式和破口大小。圖9為采用等效塑性應變準則獲得的破壞模式，可以看出與考慮應力狀態的準則得到的破壞模式具有較大差異。表明考慮應力狀態的材料失效準則對于準確預測花瓣型破口具有重要作用。

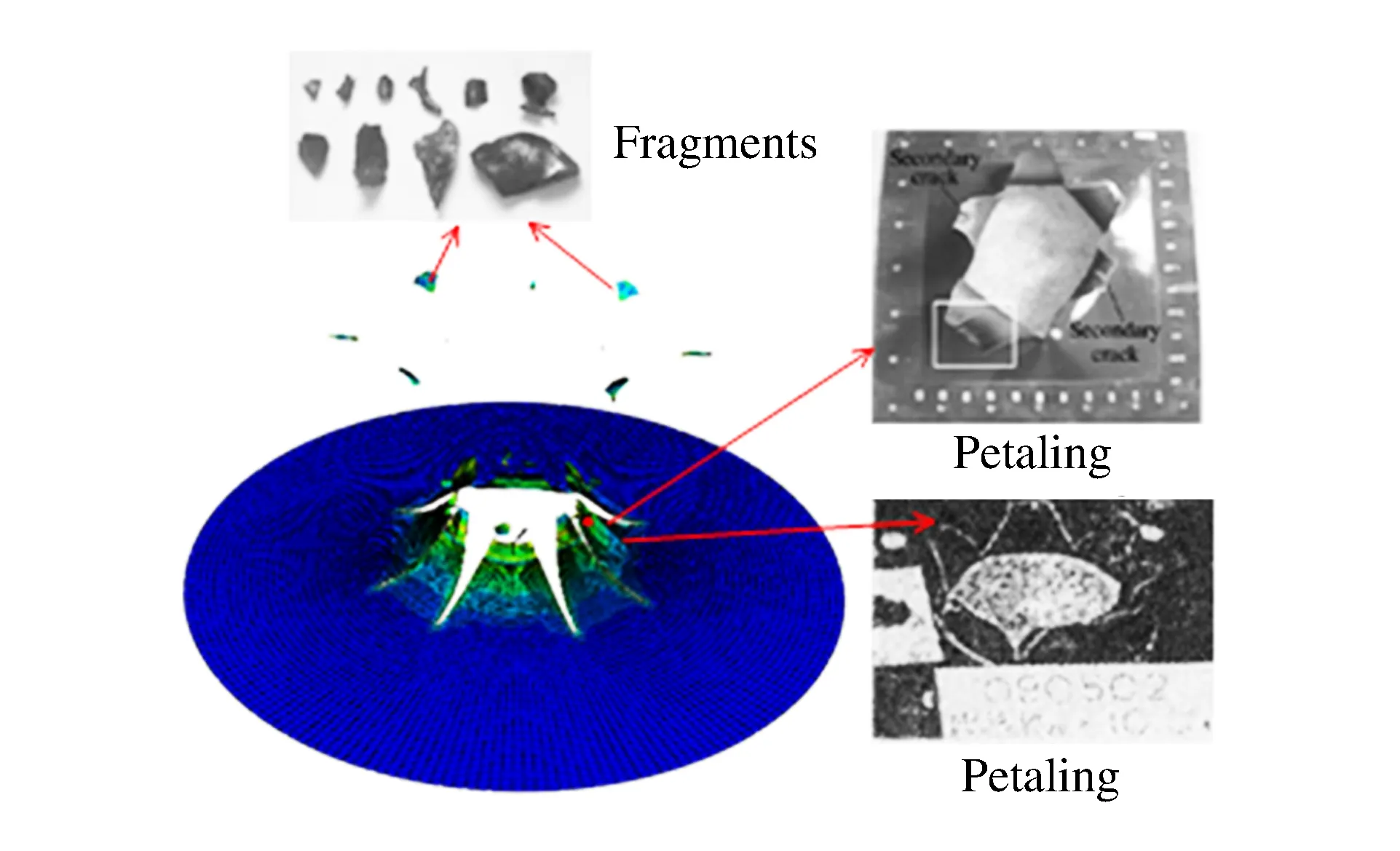
圖8 薄板形成的花瓣與碎片Fig.8 Petaling and fragments from the thin pate

圖9 等效塑性應變準則獲得的破壞模式Fig.9 Failure mode with equivalent plastic strain criterion

4 結 論

花瓣型破口是最基本的爆炸破壞模式之一，僅依據單軸受拉或雙軸受拉應力狀態開展計算分析，會造成破壞機理揭示不準確。通過開展船用鋼材料斷裂特性實驗，基于多軸應力狀態下的艦船用鋼失效準則，對局部沖擊載荷作用下花瓣型破口的形成過程、各典型位置受力狀態、損傷特性等進行了分析。得到以下結論：(1)考慮多軸應力損傷的艦船用鋼失效準則能有效預測受力狀態復雜的花瓣狀破口；(2)花瓣型破口的形成主要分為蝶形凹陷、中心區域裂紋擴展、花瓣形成與翻轉等3個階段；(3)花瓣型破口的裂紋區和非裂紋區受力復雜，除早期受拉伸作用外，后期受震蕩的壓縮和剪切作用，破口預測須考慮應力狀態對損傷特性的影響；(4)花瓣形成過程中，第1階段和第3階段均勻變形，第2階段局部損傷迅速形成，花瓣卷曲會造成花瓣根部的二次損傷。

[1] Scheffler D R, Zuka J A. Practical aspects of numerical simulation of dynamic events: material interfaces[J]. International Journal of Impact Engineering, 2000,24(8):821-842.

[2] Jacob N, Nurick G N, Langdon G S. The effect of stand-off distance on the failure of fully clamped circular mild steel plates subjected to blast loads[J]. Engineering Structures, 2007,29(10):2723-2736.

[3] 牟金磊,朱錫,張振華.水下爆炸載荷作用下加筋板變形及開裂試驗研究[J].振動與沖擊,2008,27(1):57-61. Mu Jinlei, Zhu Xi, Zhang Zhenhua. Experimental study on deformation and rupture of stiffed plates subjected to underwater shock[J]. Journal of Vibration and Shock, 2008,27(1):57-61.

[4] 陳長海,朱錫,侯海量,等.近距空爆載荷作用下固支方板的變形及破壞模式[J].爆炸與沖擊,2012,32(4):368-375. Chen Changhai, Zhu Xi, Hou Hailiang,et al. Deformation and failure modes of clamped square plates under close-range air blast loads[J]. Explosion and Shock Waves, 2012,32(4):368-375.

[5] 陳長海,朱錫,侯海量,等.近距空爆載荷作用下雙層防爆艙壁結構抗爆性能仿真分析[J].海軍工程大學學報,2012,24(3):26-34. Chen Changhai, Zhu Xi, Hou Hailiang, et al. Numerical analysis of blast resistance of double-layer bulkhead structures subjected to close-rang air blast[J]. Journal of Naval University of Engineering, 2012,24(3):26-34.

[6] Bao Y, Wierzbicki T. On fracture locus in the equivalent strain and stress triaxiality space[J]. International Journal of Mechanical Sciences, 2004,46(1):81-98.

[7] Li Xiaobin, Li Ying, Zheng Yuanzhou. Influence of stress wave on dynamics damage character of ship-build low-carbon steel based on low-velocity Taylor impact bar[J]. Journal of Ship Mechanics, 2014,18(12):1495-1504.

[8] Bao Y, Wierzbicki T. On the cut-off value of negative triaxiality for fracture[J]. Engineering Fracture Mechanics, 2005,72(7):1049-1069.

[9] 金屬材料室溫拉伸試驗方法:GB/T 228-2002[S].北京:中國標準出版社,2002:1-38.

[10] 劉敬喜,崔濛,龔榆峰.船舶碰撞仿真失效準則比較[J].中國艦船研究,2015,10(4):79-85. Liu Jingxi, Cui Meng, Gong Yufeng. A comparative study of failure criteria in ship collision simulations[J]. Chinese Journal of Ship Research, 2015,10(4):79-85.

[10] Bai Y, Wierzbicki T. A new model of metal plasticity and fracture with pressure and Lode dependence[J]. International Journal of Plasticity, 2008,24(6):1071-1096.

[11] 李營.液艙防爆炸破片侵徹作用機理研究[D].武漢:武漢理工大學,2014:23-24.

[12] Nurick G N, Radford A M. Deformation and tearing of clamped circular plates subjected to localized central blast load[C]∥Recent Developments in Computational and Applied Mechanics. Barcelona, 1997:276-301.

(責任編輯 張凌云)

Mechanism research of thin plate petaling under local loading based on multiaxial stress damage

Li Ying1,2, Wu Weiguo1, Zhang Lei2, Du Zhipeng2, Zhang Wei2, Zhao Pengduo2

(1.SchoolofTransportation,WuhanUniversityofTechnology,Wuhan430063,Hubei,China;2.NavalAcademyofArmament,Beijing100161,China)

A failure criterion considering multiaxial stress state was proposed based on the thin plate damage testing. According to the evaluation of the stress state variation and damage level of the cracking and non-cracking areas, the following conclusions can be reached: (1) the petaling phenomenon of the thin plate used for naval ships can be forecasted effectively by the proposed failure criterion; (2) the petaling procedure can be divided into three distinct stages consisting of butterfly depressing, central area cracking, and petal processing; (3) the stress states of the cracking area and the non-cracking area are complicated, and the stress state’s influence on the damage characteristics should be considered in predicting the petaling crevasse; (4) during the petaling, the central area will sink homogeneously, the cracking will result in large local deformation, and the petal cusps’ curve will lead to a secondary damage to the petal roots.

petaling; stress triaxiality; stress state; failure criterion

10.11883/1001-1455(2017)03-0554-06

2015-09-17；

2016-05-22

國家自然科學基金項目(51509196);中央高校專項基金項目(2014-yb-20); 非線性力學國家重點實驗室開放基金項目(LNM201505)

李 營(1988— )，男，博士研究生; 通信作者: 張 磊,freda_zl@126.com。

O346.5;U668.2 國標學科代碼： 13015

A