彈體斜侵徹混凝土靶的實驗研究及其數值模擬*

薛建鋒，沈培輝，王曉鳴

(南京理工大學智能彈藥技術國防重點學科實驗室，江蘇 南京 210094)

彈體斜侵徹混凝土靶的實驗研究及其數值模擬*

薛建鋒，沈培輝，王曉鳴

(南京理工大學智能彈藥技術國防重點學科實驗室，江蘇 南京 210094)

以彈體斜侵徹混凝土的彈道特性為研究內容，通過侵徹實驗與數值模擬得到了不同速度下的侵徹深度、開坑尺寸、偏轉角等參數，實驗結果與模擬結果吻合較好。研究結果表明：傾角對開坑深度和開坑形狀影響很大；傾角越大，對侵徹深度和偏轉角的影響越明顯，彈體偏轉角隨著速度的增大呈現減小的趨勢；當傾角增至一定角度后發生跳彈現象，據此得到跳彈極限角與傾角、侵徹速度的關系。

彈體；斜侵徹；混凝土靶；彈道特性；偏轉角

長期以來，各國武器研發人員一直著力于混凝土類硬目標的侵徹效應研究。美國在混凝土靶的侵徹研究方面起步較早，陸續有相關文獻發表[1-7]。中國學者對彈體斜侵徹混凝土的研究也進行了大量的探討[8-10]。武海軍等[11]、馬愛娥等[12]、呂中杰等[13]和王可慧等[14]進行了彈體斜侵徹混凝土靶的實驗，得到了彈體對混凝土靶的斜侵徹破壞效應及彈道特性等參數。從斜侵徹實驗中發現彈體發生一定程度的偏轉甚至跳彈，因此研究彈體斜侵徹混凝土時彈道偏轉是有必要的。在斜侵徹研究中彈道偏轉的概念已基本明確，但相關的實驗研究仍有待深入。本文就傾角和速度兩方面對彈道偏轉的影響進行研究。首先利用25 mm滑膛炮對半無限混凝土靶進行不同傾角的侵徹實驗，得到不同工況彈體的彈道軌跡和混凝土靶的破壞效應，結合數值模擬結果對斜侵徹彈道軌跡進行定量分析，最后得到速度和傾角對彈道偏轉的影響規律。

1 斜侵徹混凝土實驗

1.1 實驗方法及材料

以滑膛炮作為發射設備進行斜侵徹混凝土實驗，炮口到混凝土靶距離為10 m，實驗現場布置如圖1所示。

圖1 實驗現場示意圖 Fig.1 Schematic diagram of experiment set

圖2 彈體和混凝土靶Fig.2 Projectiles and concrete

實驗彈體直徑為10 mm，彈長為70 mm，CRH(彈體頭部曲率半徑與彈體直徑之比)為4，質量為80 g。彈體材料采用高強度鋼35CrMnsiA，淬火后硬度HRC為45，彈體實物見圖2。實驗用的混凝土靶為C40混凝土靶，整個混凝土靶為圓柱形，參照鉆地彈侵徹混凝土靶實驗研究中采用的靶板設計標準：靶板直徑取彈徑的30倍以上，此時可忽略靶板的邊界效應。考慮射擊精度彈著點與邊界最小距離滿足上述要求，將實驗靶體的直徑擴大為800 mm。為了方便澆注混凝土靶且保證侵徹后靶體的完整性，靶板外圍采用3 mm厚的鋼圈加固。養護后的靶體經過靜態力學性能測試，混凝土靶的平均抗壓強度為37.2 MPa，混凝土實物如圖2所示。

1.2 實驗結果

實驗中彈體速度為805～1 222 m/s。實驗后的彈體保持完整，彈體沒有明顯的變形。圖3為實驗后的混凝土靶典型破壞情況，在傾角較小時混凝土靶面開坑區近似圓形，形成了相對于著靶點近似對稱的開坑區，混凝土靶正面無明顯徑向裂紋延伸到靶板邊緣，說明邊界效應可以忽略且符合半無限靶條件，實驗數據真實可信。實驗結果見表1，表1中參量意義如圖3所示，v為速度，β為傾角，S為彈道長度，Xd為彈坑橫向最大長度，Yd為彈坑縱向最大長度，h為開坑深度，Xp為相對彈著點的橫向偏移量，Yp為最大有效侵徹深度，δ為偏轉角，姿態角為ζ(ζ=β+δ)，見圖3(d)。

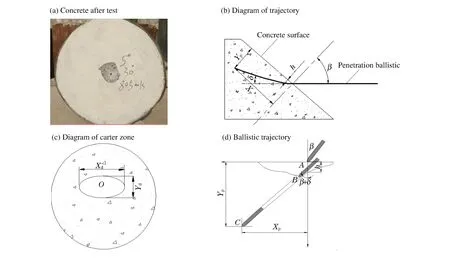
圖3 傾角侵徹靶面及彈道軌跡Fig.3 Obliquely penetrated target surface and ballistic trajectory

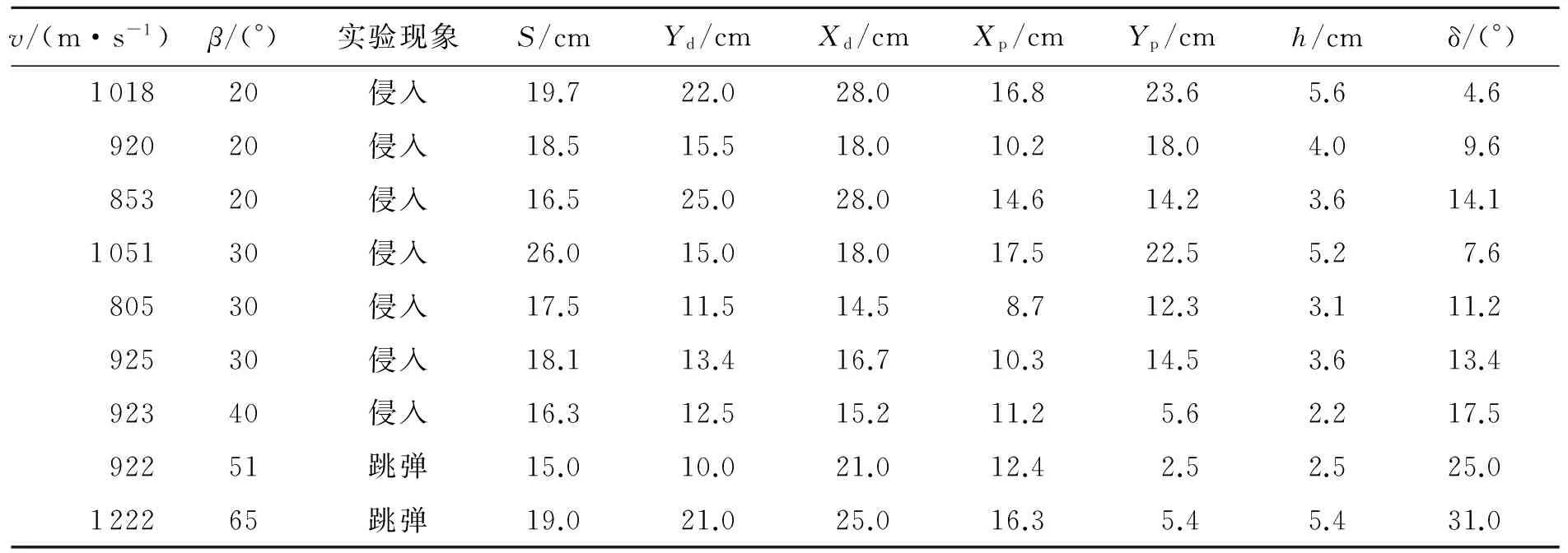
v/(m·s-1)β/(°)實驗現象S/cmYd/cmXd/cmXp/cmYp/cmh/cmδ/(°)101820侵入19.722.028.016.823.65.64.692020侵入18.515.518.010.218.04.09.685320侵入16.525.028.014.614.23.614.1105130侵入26.015.018.017.522.55.27.680530侵入17.511.514.58.712.33.111.292530侵入18.113.416.710.314.53.613.492340侵入16.312.515.211.25.62.217.592251跳彈15.010.021.012.42.52.525.0122265跳彈19.021.025.016.35.45.431.0

2 斜侵徹混凝土靶的數值模擬

2.1 有限元模型

圖4 有限元模型Fig.4 Finite element model

模型中彈體直徑為10 mm，彈體長度為70 mm，CRH為4(頭部圓弧半徑為40 mm)，為了減小邊界約束對侵徹效果的影響，混凝土靶尺寸大小為50 mm×250 mm×250 mm。利用彈靶結構和受力載荷的對稱性，取實體模型的1/2進行建模和求解。網格采用智能網格，靶板中間20 mm區域的網格劃分密集，其他區域網格劃分稀疏。為了消除靶板背面反射應力波的影響，靶板背面設定了無反射邊界條件，對彈體和混凝土靶對稱面上的節點設置了對稱約束，對混凝土側面施加邊界條件用以模擬靶體被固定的情況，有限元模型如圖4所示。

2.2 材料模型和狀態方程

觀察實驗回收的彈體發現，在侵徹過程中彈體基本不變形，基本保持剛性。因此數值模擬中，彈體選用剛性材料模型描述，彈體密度為7.83 g/cm3。彈體與混凝土靶之間的接觸算法選擇了LS-DYNA軟件自帶的Surface-to-Surface面面接觸算法。混凝土靶的強度模型采用了HJC累積損傷材料模型，狀態方程為Grüneisen狀態方程，混凝土材料參數如表2所示，其中：ρ為混凝土密度；量綱為一的內聚力強度A為給定靜水壓力下完全斷裂強度與無損強度的比值；B為量綱一壓力強化系數；N為量綱一壓力硬化；C為應變率敏感系數；Smax為混凝土所能夠達到的最大強度；G為剪切模量；D1和D2為混凝土的損傷常數；εfmin為混凝土破碎的最小塑性應變；pc為壓垮的靜水壓力；μc為壓垮的體積應變；K1、K2、K3為壓力常數；μ1為壓實體積應變；T為混凝土的最大拉伸強度。

表2 混凝土材料模型參數

3 實驗結果與模擬結果對比

采用電割方法將混凝土靶割開，測量侵徹彈道及跳彈參數。圖5為速度805 m/s、傾角為30°的侵徹實驗結果，混凝土表面的彈坑形狀近似圓形，橫縱向尺寸分別為14.5和11.5 cm，彈坑深度為3.1 cm。根據表1的實驗數據得到的彈坑深度隨速度的增加而增加，靶面破壞面積隨傾角的增加而增加。由于侵徹過程中的高溫高壓作用，整個侵徹彈道表面較為光滑，彈道周圍布滿白色混凝土粉末和明顯壓實痕跡。根據圖3(d)中的彈道特征和文獻[13]，斜侵徹過程分為彈坑區、滑移區和隧洞。彈體撞擊混凝土靶時，表面混凝土松動并脫落，此時頭部受到的阻力較小，因此彈體運動姿態基本不變。伴隨著侵徹的繼續，頭部上下表面所受的阻力嚴重不對稱產生偏轉力矩，使得彈體側向滑移。隨著侵徹深度的繼續增大，頭部所受的混凝土阻力近似一致，隧洞形成。進入隧洞后，周圍混凝土介質的約束相等，彈體的偏轉過程結束，彈體以ζ的角度繼續擠壓混凝土靶，此時所受阻力集中于彈體頭部區域。實驗發現，傾角對滑移區長度有明顯影響。傾角增加，滑移區長度增大，彈坑區與隧洞長度相應縮短。當隧洞長度降為零時，發生跳彈現象。

圖5 侵徹效果Fig.5 Penetration effect

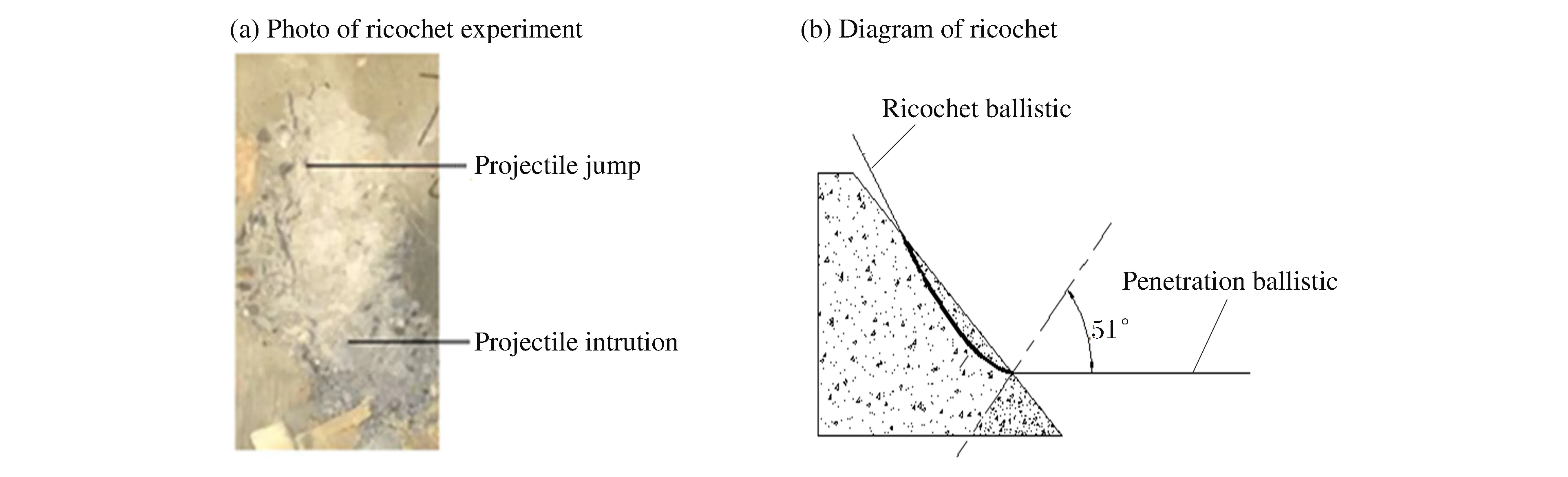
圖6 跳彈Fig.6 Ricochet

斜侵徹過程中彈體受到阻力的不對稱。由于侵徹阻力與運動方向不一致，彈體的運動方向不斷發生改變。當運動方向偏離混凝土靶方向時，彈體就會飛出靶面發生跳彈。彈體在傾角為51°、速度達到922 m/s，發生跳彈現象，如圖6所示。侵入彈道發生偏轉并從混凝土靶表面飛出，跳飛彈道與靶面法線夾角為80°左右，侵徹深度為2.5 cm。在彈靶交界區域內，彈道上方混凝土材料也會由于應力波作用而全部脫落，最終形成橢圓形彈坑。

采用建立的有限元模型，用實測到的速度進行數值模擬計算，得到不同工況下的垂直侵徹深度Yp，圖7和表3為實驗結果和數值模擬結果的對比，兩者吻合較好。圖8～9為彈體最大侵徹深度和偏轉角與傾角之間的關系。跳彈發生前，偏轉角與傾角近似成線性關系，傾角增大，彈道彎曲曲率增大，橫向偏移量也隨之增大，最終導致侵徹深度急劇降低。傾角超過40°后偏轉角急劇增大。當傾角大于51°時發生跳彈現象。跳彈區的彈坑深度明顯減小。

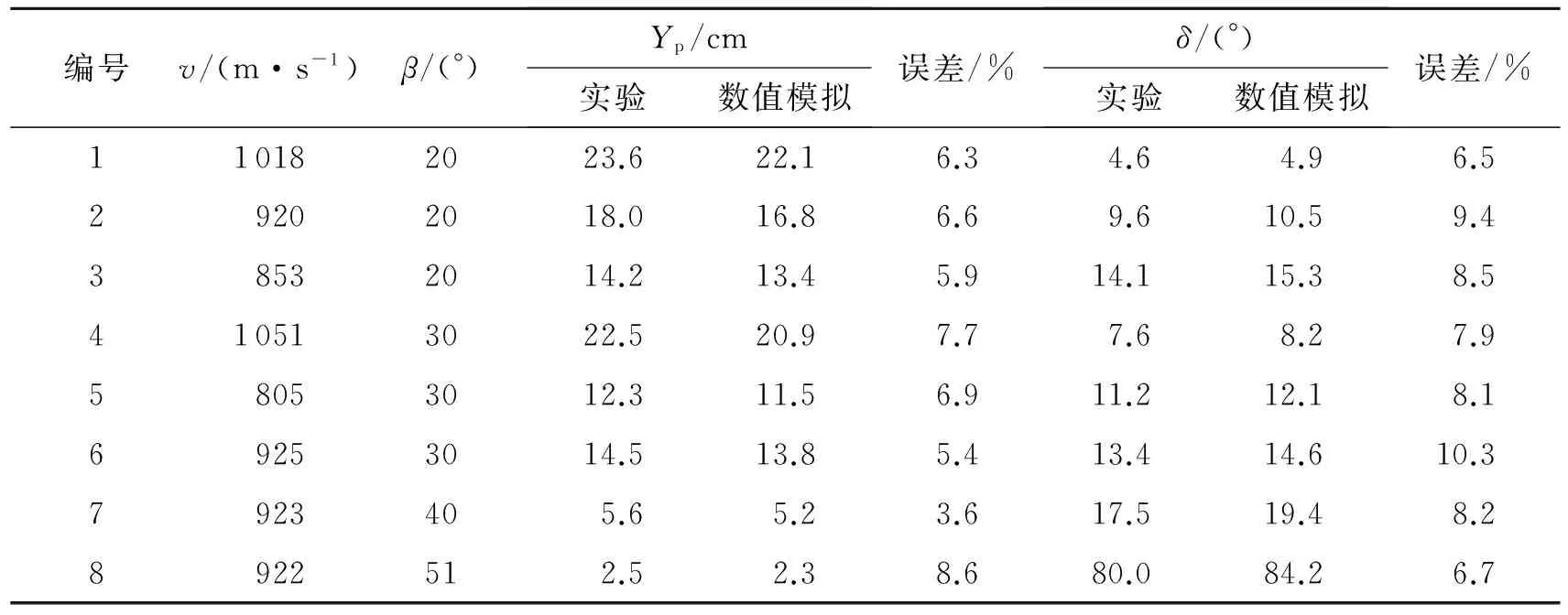
表3 彈體實驗與數值模擬結果對比

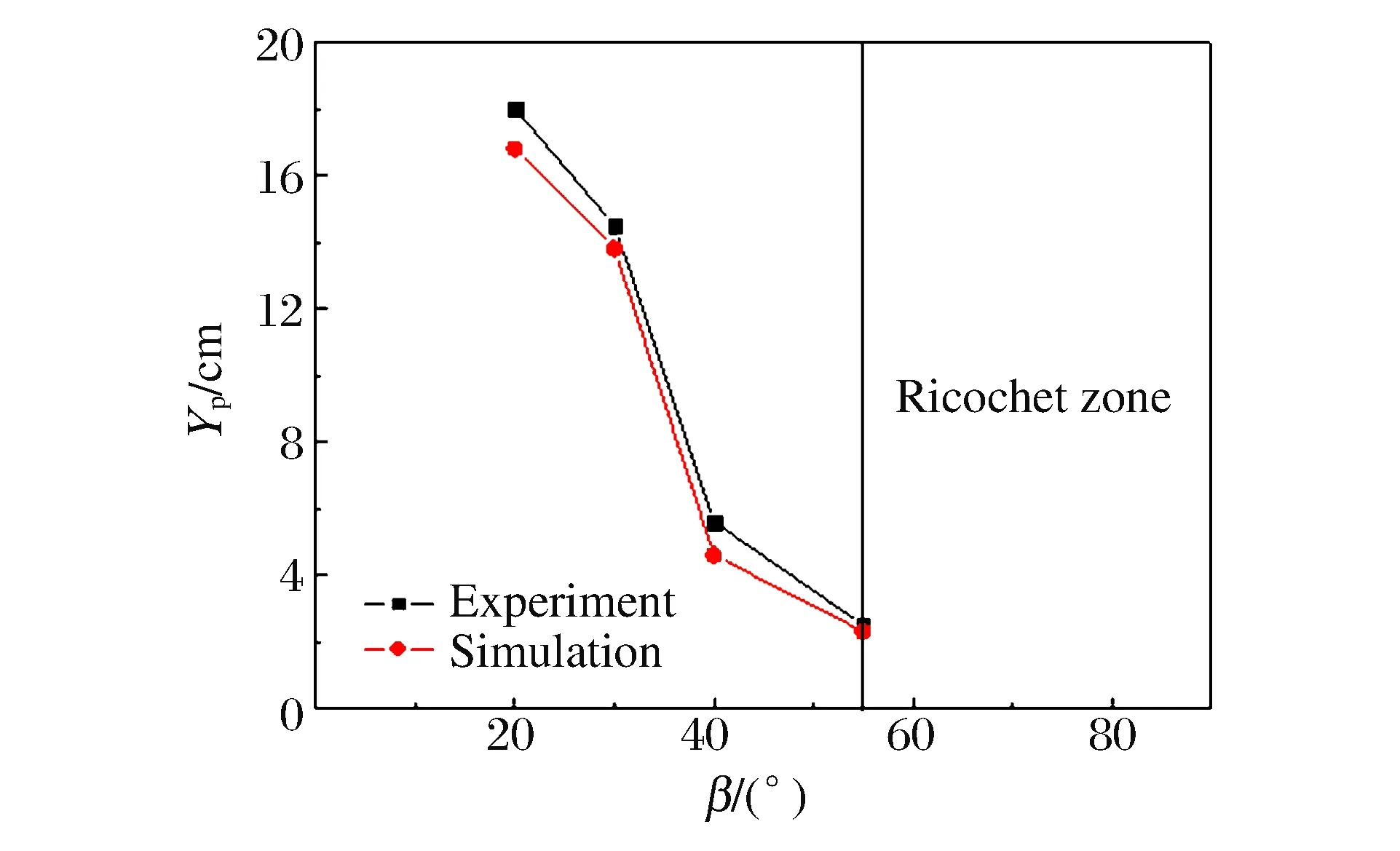
圖8 侵徹深度與傾角的關系Fig.8 Ralation between penetration depth and oblique angle

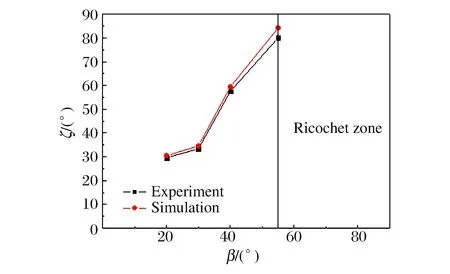
圖9 姿態角與傾角的關系Fig.9 Ralation between attitude angle and oblique angle

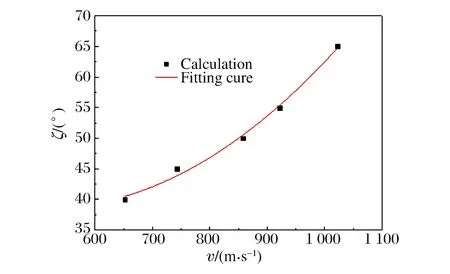
圖10 跳彈極限角與速度的關系Fig.10 Relation between ricochet angle and velocity

對跳彈極限角進行計算，得到：當入射速度v為652、743、858、922、1 022 m/s時，跳彈極限角η分別為40°、45°、50°、55°、65°。對該結果進行二次多項式擬合，擬合曲線如圖10所示，跳彈極限角η(°)與速度v(m/s)的函數關系式為：

η=65.3-0.1v+0.02v2

(1)

可見彈體入射速度越高，抗跳飛能力越高，跳彈極限角越大。

4 傾角和速度對彈道偏轉的影響分析

為了進一步研究侵徹過程中彈道特性，對彈體侵徹混凝土的過程進行數值模擬。不同傾角下彈道軌跡、最大侵徹深度與傾角變化關系如圖11和12所示。從圖中可以看出，隨著傾角的增大，侵徹深度逐漸減小，當傾角達到40°時，混凝土自由表面對侵徹彈道影響嚴重，彈體頭部上下表面受力不對稱，彈道軌跡向上偏轉。當傾角增加到57°時，發生跳彈現象。

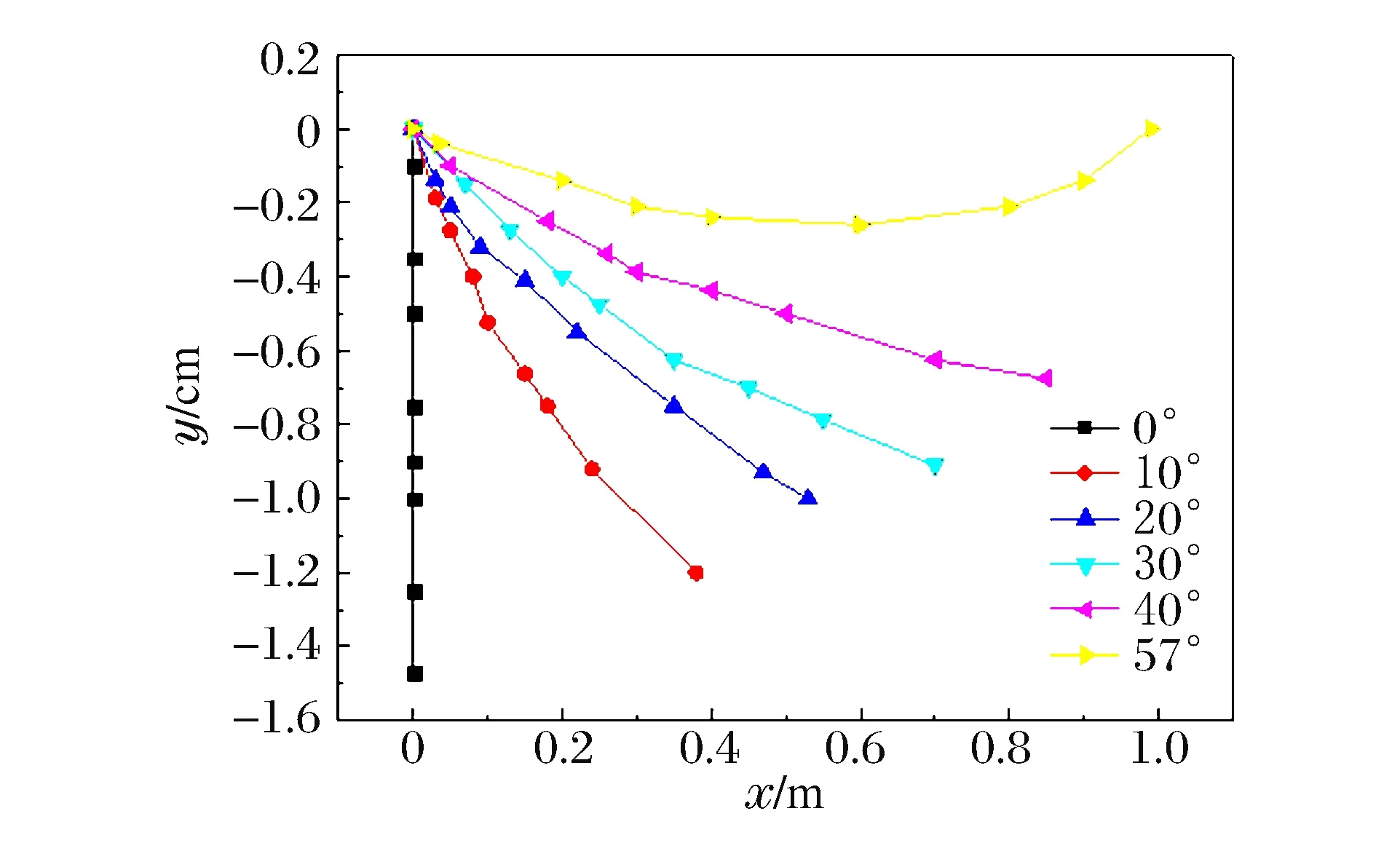
圖11 不同傾角下的彈道軌跡Fig.11 Ballistic trajectory due to different oblique angle

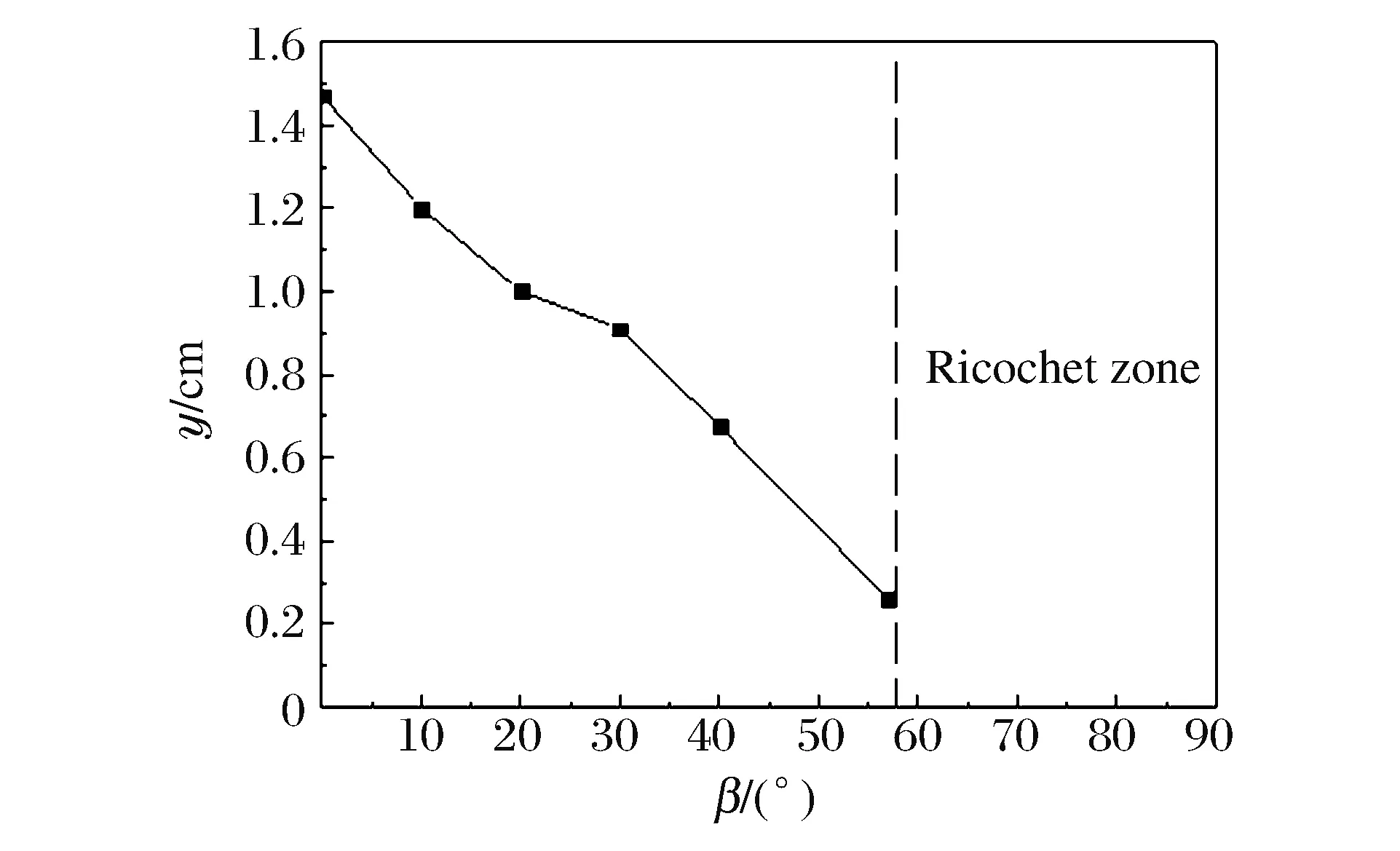
圖12 侵徹深度隨傾角變化關系Fig.12 Penetration depth vs. oblique angle

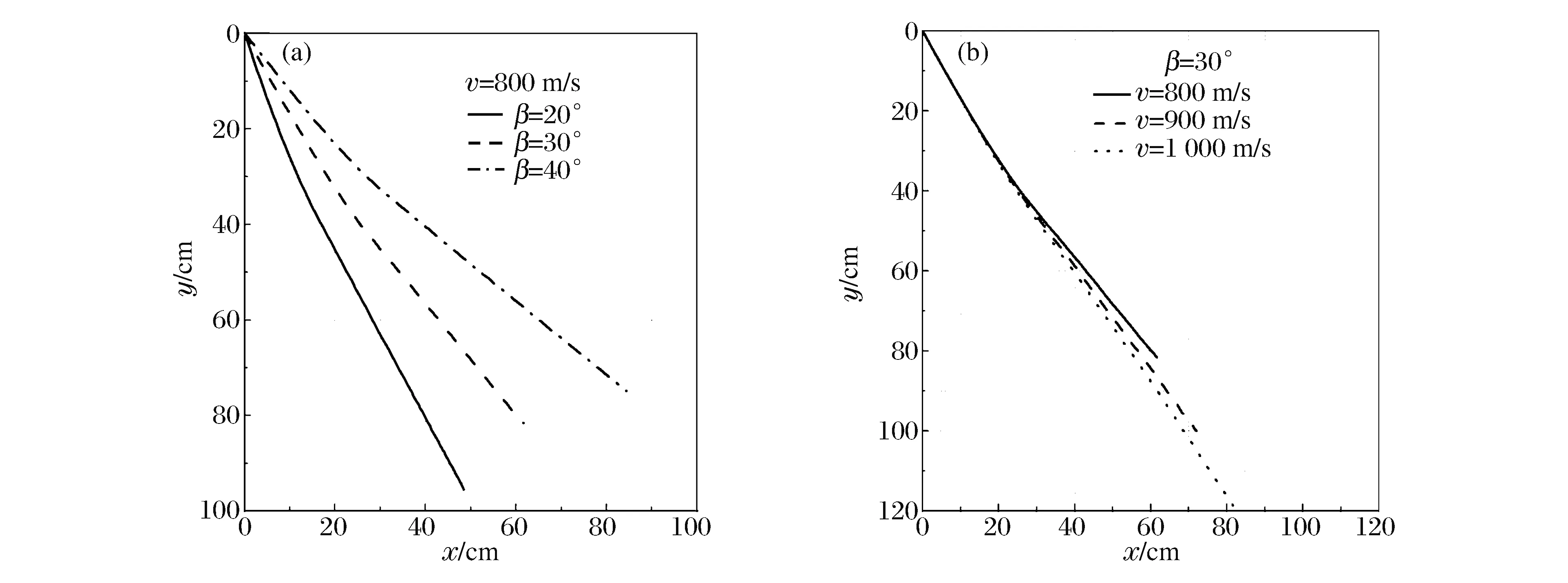
圖13 斜侵徹下的彈道軌跡變化Fig.13 Ballistic trajectory under oblique penetration

圖14 斜侵徹下的偏轉角變化Fig.14 Deflection angle under oblique penetration

圖13給出了傾角和入射速度對侵徹軌跡的影響。從圖13中可知，速度一定、不同傾角的彈道都發生了一定程度的彎曲。初期彈道彎曲程度隨侵徹深度的增加逐漸變小，最終彈體基本沿著直線運動。同一傾角、不同速度彈體的運動軌跡幾乎是重合的，隨著時間增加，軌跡逐漸分離，發生了不同程度的偏轉，最終彈體彈道沿直線發展，直到速度降為零，侵徹結束。

圖14為偏轉角與速度和傾角的關系。在侵徹初期彈體的姿態角逐漸增大，侵徹中期姿態角的變化略有波動，最后趨于一個穩定值。初始速度增大，姿態角變化曲線在某一時間段內的斜率隨著速度的增加而呈減小的趨勢，表明速度越大，姿態角變化程度越小。

5 結 論

本文中開展了彈體斜侵徹混凝土靶實驗，按照實驗條件進行數值模擬，得到了以下結論：

(1) 計算得到跳彈極限角與速度的關系式，并得到兩者之間的規律：速度越高，抗跳飛能力越高，跳彈極限角越大。

(2) 彈體垂直侵徹深度隨傾角的增大而減小，滑移量隨著傾角的增大而增大。偏轉角隨傾角的增加而增大。

[1] Gold V M, Vradis G C, Pearson J C. Concrete penetration by eroding projectiles:Experiments and analysis[J].Journal of Engineering Mechanics, 1996,122(2):145-152.

[2] Forrestal M J, Frew D J, Hanchak S J, et al. Penetation of grount and concrete targets with ogive-nose steel projectiles[J]. International Journal of Impact Engineering, 1996,18(5):465-476.

[3] Macek R W, Duffey T. Finite cavity expansion method for near-surface effects and layering during earth penetration[J]. Modeling and simulation based engineering, 1998,10(2):1138-1143.

[4] Longcope D B, Tabbara M R, Jung J. Modeling of oblique penetration into geologic targets using cavity expansion penetrator loading with target free-surface effects: SAND99-1104C[R]. Albuquerque, New Mexico, USA: Sandia Nation Laboratories, 1999.

[5] Warren T L, Poormon K L. Penetration of 6061-T6511 aluminum targets by ogive-nosed VAR 4340 steel projectiles at oblique angles: Experiments and simulations[J]. International Journal of Impact Engineering, 2001,25:993-1022.

[6] Forrestal M J, Frew D J, Hicheron J P, et al. Penetration of concrete targets with deceleration time measurement[J]. International Journal of Impact Engineering, 2003,28(5):479-497.

[7] Lampert S, Jeanquartier R. Perforation of concrete targets by an eroding tungsten-alloy rod[C]∥Proceedings of the 22th International Symposium on Billistics. Vancouver, Canada, 2005:838-843.

[8] 劉小虎,劉吉,王乘,等.彈丸低速垂直侵徹無鋼筋混凝土的實驗研究[J].爆炸與沖擊,1999,19(4):323-328. Liu Xiaohui, Liu Ji, Wang Cheng, et al. Experimental study on the projectile penetration normally into a plain concrete[J]. Explosion and Shock Waves, 1999,19(4):323-328.

[9] 王明洋,鄭大亮,錢七虎.彈體對混凝土介質侵徹、貫穿的比例換算關系[J].爆炸與沖擊,2004,24(2):108-114. Wang Mingyang, Zheng Daliang, Qian Qihu. The scaling problems of penetration and perforation for projectile into concrete media[J]. Explosion and Shock Waves, 2004,24(2):108-114.

[10] 王浩,陶如意.截卵形彈頭對混凝土靶侵徹性能的試驗研究[J].爆炸與沖擊,2005,25(2):171-175. Wang Hao, Tao Ruyi. Experimental study on the penetration performance of truncated-ogive nose projectile[J]. Explosion and Shock Waves, 2005,25(2):171-175.

[11] 武海軍,黃風雷,王一楠.高速彈體非正侵徹混凝土試驗研究[C]∥第八屆全國爆炸力學學術會議文集.吉安,2007:488-494.

[12] 馬愛娥,黃鳳雷.彈體斜侵徹鋼筋混凝土的試驗研究[J].北京理工大學學報,2007,27(6):482-486. Ma Ai’e, Huang Fenglei. Experimental research on oblique penetration into reinforced concrete[J]. Transactions of Beijing Institute of Technology, 2007,27(6):482-486.

[13] 呂中杰,徐鈺巍,黃鳳雷.彈體斜侵徹混凝土過程中的方向偏轉[J].兵工學報,2009,30(2):301-304. Lü Zhongjie, Xu Yuwei, Huang Fenglei. Transverse deflection of projectile obliquely penetrating into concrete[J]. Acta Armamentarii, 2009,30(2):301-305.

[14] 王可慧,寧建國,李志康,等.高速彈體非正侵徹混凝土靶的彈道偏轉試驗研究[J].高壓物理學報,2013,27(4):561-566. Wang Kehui, Ning Jianguo, Li Zhikang,et al. Ballistic trajectory of high-velocity projectile obliquely penetrating concrete target[J]. Chinese Journal of High Pressure Physics, 2013,27(4):561-566.

(責任編輯 王小飛)

Experimental study and numerical simulation of projectile obliquely penetrating into concrete target

Xue Jianfeng, Shen Peihui, Wang Xiaoming

(ZNDYMinisterialKeyLaboratory,NanjingUniversityofScienceandTechnology,Nanjing210094,Jiangsu,China)

The ballistic characteristics of the projectile obliquely penetrating into the concrete target were investigated, with such data as the penetration depth, crater depth and diameter, deflection angle obtained via the experiments and simulation calculation. The results from simulation agree well with those from the experiments. The results show that the oblique angle has great influence on the crater zone. The greater the oblique angle, the greater the projectile’s deflection; the greater the impact velocity, the less the influence of the ballistic deflection angle; and the ricochet occurs when the oblique angle increases to a certain degree. Thus the relationship was identified between the ricochet angle and the oblique angle and the penetration velocity.

projectile; oblique penetration; concrete targets; ballistic characteristic; transverse deflection angle

10.11883/1001-1455(2017)03-0536-08

2015-11-05；

2016-01-20

國家重點基礎研究發展計劃(973計劃)項目(61314302)

薛建鋒(1987- )，男，講師；通信作者： 沈培輝，sphjy8@mail.njust.edu.cn。

O385 國標學科代碼： 13035

A