基于量綱分析理論的煤塵爆炸能量預測模型*

李雨成，劉天奇，周西華

(1.遼寧工程技術大學安全科學與工程學院,遼寧 阜新 123000;2.遼寧工程技術大學礦山熱動力災害與防治教育部重點實驗室,遼寧 阜新 123000)

基于量綱分析理論的煤塵爆炸能量預測模型*

李雨成1,2，劉天奇1,2，周西華1,2

(1.遼寧工程技術大學安全科學與工程學院,遼寧 阜新 123000;2.遼寧工程技術大學礦山熱動力災害與防治教育部重點實驗室,遼寧 阜新 123000)

為預測煤塵爆炸能量，基于量綱分析理論建立煤塵爆炸能量預測模型。選取爆炸能量E、空氣密度ρ和大氣壓強p的量綱為導出量綱。根據量綱分析Π定理得出含有待定參數的具有普適性的能量預測模型。通過小型煤塵爆炸性實驗設計，測定10次爆炸最長火焰長度平均值l0、10次最長火焰長度出現時間平均值t0與該小型煤塵爆炸中釋放能量E0，確定模型中參數為0.467。對模型變量t、E、l的函數關系進行合理性檢驗。通過實測的15組不同時刻的火焰長度進行模型變量t、l冪指關系檢驗。檢驗結果表明：量綱選取完備，預測模型科學合理。

煤塵爆炸;能量預測;量綱分析;預測模型

煤礦井下作業中，一旦掘進面等處產生的浮塵遇到明火，極易發生爆炸事故[1-2]。煤塵爆炸在傳播過程中，沖擊波和火焰面釋放的能量給巷道結構、生產設備及作業人員帶來極大損害[3-4]。煤塵爆炸屬于多次連環的有可燃懸浮顆粒參與的化學爆炸。對煤塵爆炸能量的研究主要集中于壓力波和火焰波兩方面。李慶釗等[5]利用20 L球形裝置研究了煤塵濃度、環境初壓等因素與爆炸能量的關系。程磊[6]研究了受限分岔管道、雙向分岔管道、截面突變管道內煤塵爆炸沖擊波的變化規律。張延松[7]、李潤之[8]和王新等[9]研究了大型實驗巷道中瓦斯誘導煤塵爆炸產生的壓力波、火焰波的傳播過程。李雨成等[10-11]研究了不同煤質的煤塵爆炸火焰傳播特性，并建立了火焰長度預測模型。由于煤塵爆炸能量的數量級較大，不便于測試，因此，本文中基于量綱分析理論建立煤塵爆炸能量預測模型，以期為高數量級的爆炸能量預測提供理論基礎。

1 基于量綱分析理論的煤塵爆炸能量預測模型

1.1 基本量綱與導出量綱的選取

量綱是自然界中物理量的單位，分為基本量綱和導出量綱[12-13]。本文中預測煤塵爆炸能量選取的基本量綱為煤塵爆炸火焰長度l、煤塵質量m、時間t的量綱，分別記為：

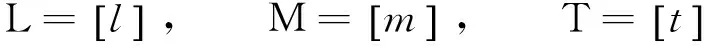
(1)

在基本量綱的基礎上可形成導出量綱，本文中采用的導出量綱有煤塵爆炸能量E、空氣密度ρ、大氣壓強p的量綱，分別記為:

(2)

根據量綱分析理論，可以找到與煤塵爆炸能量相關的變量及其之間的量綱關系。其中，量綱分析齊次原理是量綱分析理論中的重要原理，Π定理是利用量綱分析理論建模的基礎，雖然根據Π定理往往不能求出模型的具體表達式，但并不影響建模過程及本文煤塵爆炸能量的預測結果。

1.2 基于量綱分析齊次原理與Π定理的煤塵爆炸能量預測模型

將煤塵爆炸中釋放的能量記為E，在本文建模中，考慮的基本量綱有煤塵爆炸火焰傳播距離(即火焰長度)l、質量m、時間t的量綱，還考慮了動力學范疇內與之相關的物理變量空氣密度ρ與大氣壓強p的量綱。通過后文模型分析可驗證所選取變量是準確充足有效的，其具體量綱表達式已由式(2)給出。則根據量綱分析Π定理，不妨設l與t、E、ρ、p間存在如下關系式l=(t,E,ρ,p)，將其寫成隱函數形式為f(l,t,E,ρ,p)=0。根據量綱分析齊次原理中“導出量綱函數可寫成基本量綱冪函數乘積形式”的結論，可把l、t、E、ρ、p表示成基本量綱L、M、T冪函數乘積形式:

(3)

根據量綱分析Π定理，由式(3)得到量綱矩陣為:

(4)

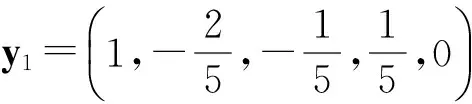
再根據Π定理，得到2個相互獨立且量綱一量π1和π2，使得F(π1,π2)=0與f(l,t,E,ρ,p)=0等價。其中，π1和π2表達式分別為:

(5)

由于π1和π2均為量綱一量且彼此相互獨立，因此兩者必然可表達成某一函數ψ形式，即:

(6)

由此得到煤塵爆炸火焰長度l關于t、E、ρ、p的函數關系。在函數ψ中，由于煤塵爆炸火焰存在時間很短，而煤塵爆炸所釋放能量很大，因此可做如下處理：

(7)

顯然對某一固定函數形式ψ，ψ(0)必為一常數，不妨令ψ(0)=。由此將l推導成關于t、E、ρ的函數關系(空氣密度ρ=1.25 kg/m3)如下：

(8)

式中:煤塵爆炸火焰持續時間t、煤塵爆炸火焰長度l均可測，只要再實測一組爆炸釋放能量E就可估計出常數，進而利用式(8)即可針對不同時刻t的火焰長度l，估計煤塵爆炸不同時刻釋放出的能量E，這對爆炸威力預測及爆炸后果評估具有重要意義。為確定常數，設計實驗如下。

2 模型待定參數確定的小型實驗設計與模型檢驗

2.1 小型煤塵爆炸實驗設計

圖1 煤塵爆炸性鑒定裝置Fig.1 Identification equipment of coal dust explosibility

對于模型(8)中存在的3個未知參數l、t、E和一個待定參數，對于不同時刻t會對應存在煤塵爆炸火焰長度l和爆炸釋放能量E，但對于時間t存在一個臨界點，即為煤塵爆炸能量釋放最大(即能量全部釋放)的時刻t0，當t>t0時，火焰長度l和釋放能量E均開始減小。為確定待定參數，可設計小型實驗思路如下。

以t0時刻為基準，通過煤塵爆炸性鑒定實驗，實驗裝置如圖1所示，可以測得t0時刻對應的最長火焰長度l0。為便于看清數據，利用高速攝像機捕捉火焰圖像，通過玻璃管上標尺刻度讀取火焰長度。10次爆炸實驗捕捉到最長火焰長度平均值為l0=0.65 m，對應10次實驗的最長火焰長度出現的時間的平均值為t0=0.015 s。再根據所選煤樣為無煙煤，其煤塵熱值Q=2.9×107J/kg，煤樣質量為1 g，進而得到該小型煤塵爆炸中釋放能量為E0=2.9×104J。

2.2 模型待定參數計算

將2.1節中實驗計算得到的l0、t0、E0代入式(8)，可計算得到待定參數為：

(9)

由此得到煤塵爆炸能量釋放預測模型為:

(10)

采用該能量預測模型，可以在已知一組爆炸t時刻火焰長度l情況下，預測爆炸各不同時刻能量釋放值。但對于該公式存在一定限制條件，即0t0時，火焰長度l開始逐漸衰減，所釋放能量E也開始衰減。

2.3 模型檢驗

2.3.1 模型變量t、E、l合理性檢驗

對于由量綱分析原理和小型煤塵爆炸性鑒定實驗設計推導出的煤塵爆炸能量預測模型(10)，當t=0時，l=0，顯然與實際情況相符，即在爆炸起始時刻，煤塵爆炸火焰長度為0，煤塵爆炸釋放能量為0。在此基礎上，由式(10)可以看出，在t∈[0,t0]范圍內，隨著爆炸后時間的增大，火焰長度、爆炸釋放能量也不斷增大，即火焰長度、爆炸釋放能量分別與爆炸時間呈冪指遞增函數關系，也驗證了模型的合理性。

2.3.2 模型變量t、l冪指關系檢驗

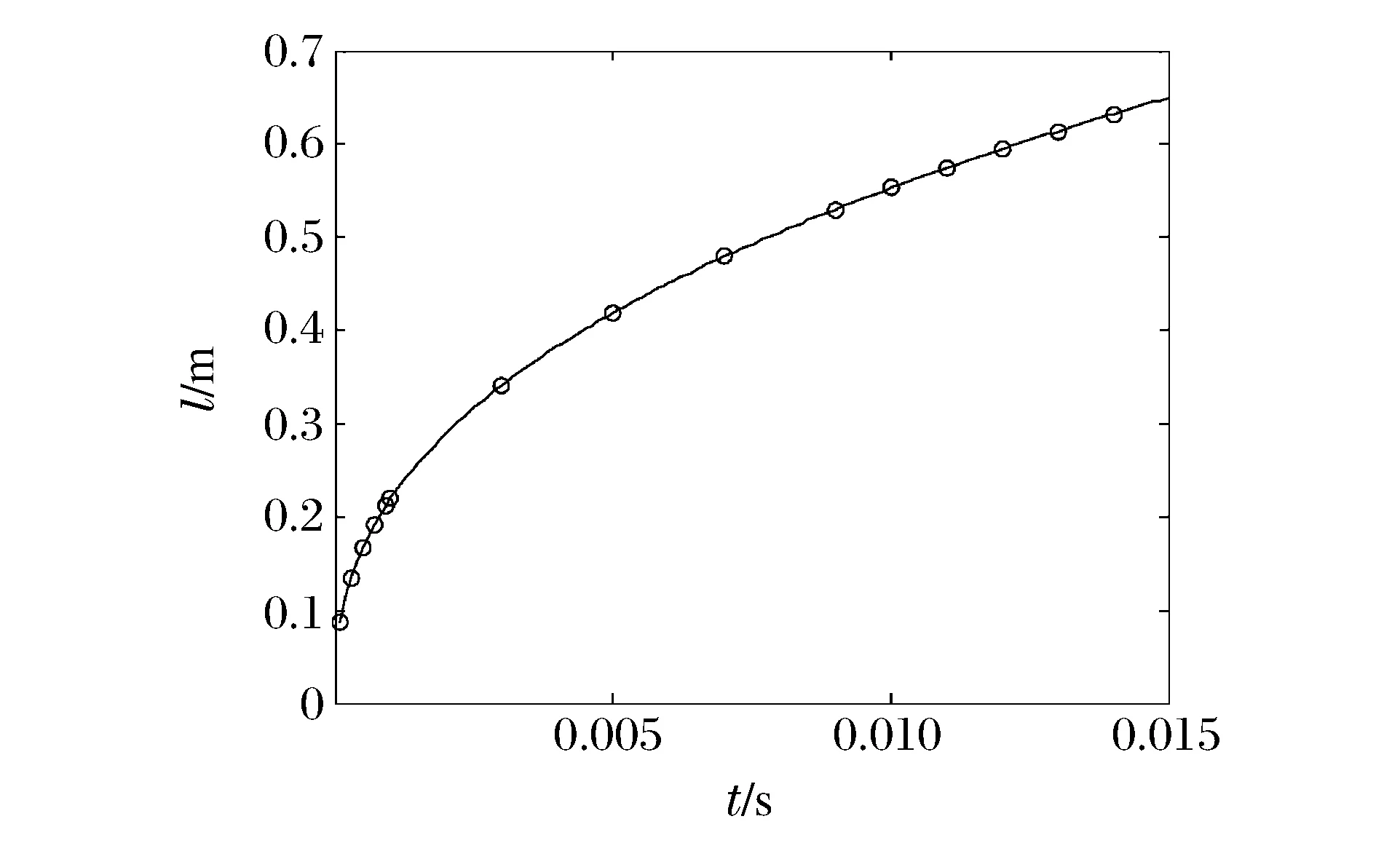
圖2 擬合結果Fig.2 Fitted result

再進一步驗證模型中冪指關系的合理性，首先暫不考慮變量E的作用，僅從l和t角度可知l正比于t的2/5次冪。為驗證該關系，利用SA8獨立型高速攝像機(每秒可最多拍攝30 000幀)捕捉的不同時刻火焰長度(為10次測試的平均值)(見表1)，進行l=atb(0

表1 不同時刻的火焰長度

2.4 應用前景分析

在預測模型(10)中，只要已知某時刻t的煤塵爆炸火焰傳播距離l，就可以利用該模型預測t時刻爆炸釋放的能量。而在煤礦現場，首先可通過技術手段確定爆源位置，在易爆區段安裝可精確測量物體運動時間的時間傳感器以及火焰傳感器，以獲取火焰傳播最遠距離和傳播時間數據，以此進行爆炸能量估算。同時，即便測試條件受限，對于煤塵爆炸火焰傳播規律的研究(包括火焰傳播距離、火焰傳播速度與時間的關系)仍然很多，文獻[6-7]等均給出火焰傳播距離與時間的關系表達式。因此，只要通過爆炸痕跡鑒定判斷出火焰傳播的最遠距離，便可推導出爆炸經歷的時間，再代入能量預測模型(10)同樣可得出結果。預測模型(10)參數變量較少，量綱選取完備合理，同時使計算過程極大簡化，省去以往復雜的偏微分方程的運算過程，降低了在模型求解時對數學理論掌握的高要求。此外，通過量綱分析方法和小型實驗室煤塵爆炸性鑒定實驗，便可預測計算出數量級相對較高的爆炸能量，大大簡化運算量，同時，預測結果對爆炸事故處理有一定參考意義與應用價值。

3 結 論

(1)根據量綱齊次原理與量綱分析Π定理構建了煤塵爆炸能量模型。選取煤塵爆炸火焰傳播距離l、質量m、時間t的量綱為基本量綱，選取爆炸能量E、空氣密度ρ和大氣壓強p的量綱為導出量綱。由Π定理得出含有未知參數l、t、E和待定參數的具有普適性和創新性的能量預測模型。

(3)通過分析模型中變量t、E與變量l的函數關系驗證了模型的合理性。利用實驗實測的15組不同時刻t的火焰長度l檢驗模型中變量t、l的冪指關系，擬合方程結果為l正比于t的0.400 2次冪，而模型中l正比于t的2/5次冪，進一步驗證了量綱選取的完備性和模型的科學性。從應用前景角度分析，該預測模型計算簡單，變量參數少，對煤礦爆炸事故危害評估具有借鑒意義和應用價值。

[1] 金龍哲.礦井粉塵防治理論[M].北京:科學出版社,2010:45-56.

[2] 李雨成.礦井粉塵防治理論及技術[M].北京:煤炭工業出版社,2015:23-38.

[3] 蔡周全,羅振敏,程方明.瓦斯煤塵爆炸傳播特性的實驗研究[J].煤炭學報,2009,34(7):938-941. Cai Zhouquan, Luo Zhenmin, Cheng Fangming. Experimental study on propagation characteristics of gas and coal dust explosion[J]. Journal of Coal, 2009,34(7):938-941.

[4] 來誠鋒,段滋華,張永發.煤粉末的爆炸機理[J].爆炸與沖擊,2010,30(3):325-328. Lai Chengfeng, Duan Zihua, Zhang Yongfa. Explosion mechanism of carbon powder[J]. Explosion and Shock Waves, 2010,30(3):325-328.

[5] 李慶釗,翟成,吳海進.基于20L球形爆炸裝置的煤塵爆炸特性研究[J].煤炭學報,2011,36(S1):119-124. Li Qingzhao, Zhai Cheng, Wu Haijin. Investigation on dust explosion characteristics using 20 L explosion sphere vessels[J]. Journal of Coal, 2011,36(S1):119-124.

[6] 程磊.受限空間煤塵爆炸沖擊波傳播衰減規律研究[D].焦作:河南理工大學,2011:79-91.

[7] 張延松.瓦斯爆炸誘導沉積煤塵爆炸研究[M].北京:中國礦業大學出版社,2011:19-31.

[8] 李潤之.瓦斯爆炸誘導沉積煤塵爆炸的數值模擬[J].爆炸與沖擊,2010,30(5):529-534. Li Runzhi. Numerical simulation of coal dust explosion induced by gas explosion[J]. Explosion and Shock Waves, 2010,30(5):529-534.

[91] 王新,李潤之,張延松.瓦斯爆炸引起沉積煤塵爆炸傳播實驗研究[J].中國安全科學學報,2009,19(4):73-77. Wang Xin, Li Runzhi, Zhang Yansong. Experimental study on the propagation laws of gas explosion inducing coal dust explosion[J]. China Safety Science Journal, 2009,19(4):73-77.

[10] 李雨成,劉天奇,陳善樂.煤質指標對煤塵爆炸火焰長度影響作用的主成分分析[J].中國安全生產科學技術,2015,11(3):40-46. Li Yucheng, Liu Tianqi, Chen Shanle. Principal component analysis of impact of coal quality index on flame length in coal dust explosion[J]. Journal of Safety Science and Technology, 2015,11(3):40-46.

[11] Li Yucheng, Liu Tianqi, Chen Shanle. The prediction model research of flame length of coal dust explosion based on coal quality indexes’ PCRA[J]. International Journal of Earth Sciences and Engineering, 2014,7(5):1777-1787.

[12] Bridgman P W. Dimensional analysis[M]. New York: Classics Press, 2013:24-31.

[13] 談慶明.量綱分析[M].北京:中國科學技術大學出版社,2005:48-59.

(責任編輯 張凌云)

An energy prediction model for coal dust explosion based on dimensional analysis

Li Yucheng1,2, Liu Tianqi1,2, Zhou Xihua1,2

(1.CollegeofSafetyScienceandEngineering,LiaoningTechnicalUniversity,Fuxin123000,Liaoning,China;2.KeyLaboratoryofMineThermo-motiveDisasterandPrevention,MinistryofEducation,LiaoningTechnicalUniversity,Fuxin123000,Liaoning,China)

To assess the coal dust explosive power, we used the dimensional analysis mathematical method to model the prediction of the energyreleased from coal dust explosion. The basic dimensions selected are those of the distance, the mass and the time, of coal dust explosion’s flame propagation. The selected output dimensions are those of explosive energy, the air density and the barometric pressure. According to the dimensional analysis Π theorem, we established the energy prediction model with unknown parameters and undetermined parameters, a model that is universally applicable. By carrying out a small-scale coal dust explosion experimental design, we determined the model parameters, and obtained the average maximum flame length of ten times of coal dust explosion, the average maximum flame time, and the released energy. The undetermined parameter was calculated as 0.467. It follows that the prediction model for coal dust explosive energy and its qualification were obtained. Based on our rationality analysis of this model, the experimental measured flame length of 15 different times of coal dust explosion was used to test the power exponent relationship. The test result verifies the completeness of the selected dimensions and the scientific rationality of the prediction model. Using fewer variable parameters, this model simplifies calculations and will provide important reference for explosion hazard assessment.

coal dust explosion; energy prediction; dimensional analysis; predicting model

10.11883/1001-1455(2017)03-0566-05

2015-09-22；

2015-12-28

國家自然科學基金項目(51204089,51274115);遼寧省教育廳科研項目(L2014131)

李雨成(1978— ),男,博士,副教授,碩士生導師,lyclntu@163.com。

O389;X936 國標學科代碼： 13035

A