梯度多胞犧牲層的抗爆炸分析*

蔡正宇,丁圓圓,王士龍,鄭志軍,虞吉林

(1.中國科學技術大學近代力學系中國科學院材料力學行為和設計重點實驗室，安徽 合肥 230026;2.寧波大學力學與材料科學研究中心，浙江 寧波 315211)

梯度多胞犧牲層的抗爆炸分析*

蔡正宇1,丁圓圓2,王士龍1,鄭志軍1,虞吉林1

(1.中國科學技術大學近代力學系中國科學院材料力學行為和設計重點實驗室，安徽 合肥 230026;2.寧波大學力學與材料科學研究中心，浙江 寧波 315211)

運用一維非線性塑性沖擊波模型和細觀有限元模型對密度梯度多胞犧牲層的抗爆炸性能進行了分析。基于率無關的剛性-塑性硬化模型，建立了描述沖擊波在多胞犧牲層中傳播的控制方程，分別給出了正、負密度梯度多胞材料在指數型爆炸載荷作用下的響應特性。研究了可正好吸收爆炸能量的梯度多胞犧牲層的臨界厚度與載荷強度、覆蓋層質量、多胞材料的密度梯度等參數之間的關系，給出了以臨界厚度和支撐端應力峰值為指標的密度梯度設計圖。運用二維細觀有限元模型驗證了基于非線性塑性沖擊波模型的抗爆炸分析的有效性。

多胞材料；犧牲層結構；爆炸載荷；沖擊波；有限元方法

多胞材料具有優異的能量吸收和抗沖擊性能，被廣泛用于汽車、列車、航空航天和軍事防護等領域[1]。梯度多胞金屬材料由于其可設計性受到廣泛關注，通過改變胞元尺寸、胞壁厚度等參數的分布情況引入密度梯度，使得材料呈現出漸進的力學性能，可望獲得更優異的能量吸收和抗沖擊性能[2]。多胞犧牲層是由覆蓋層和多胞芯層組成的夾芯結構，通常放置在被保護結構的表面。在爆炸載荷作用下，覆蓋層獲得較大的沖擊速度，芯層壓縮坍塌吸收大量的能量從而保護主體結構不發生破壞[3]。在有限的空間下，芯層厚度需要設計得盡可能小，同時被保護結構所承受的沖擊應力要維持在許可應力之下。最小芯層厚度和支撐端最小應力是犧牲層作為防護結構的兩個主要設計目標。

已有研究表明，多胞材料的密度分布對結構的沖擊響應和能量吸收影響顯著[4]。密度分布會導致應力不均勻性，在強動載荷作用下可能會在不同位置產生多個局部化變形帶。多數實驗研究局限于由均勻泡沫粘結而成的階梯式、不連續的梯度材料[5-6]。目前，對連續密度分布的多胞材料表現出的力學性能已有一定認識。在具有線性密度分布的多胞材料抗沖擊行為方面，Wang Xiaokai等[7]認為正梯度泡沫鋁可有效降低初始應力峰值，Zheng Jie等[8]認為在瞬態沖擊下，選用正、負梯度的泡沫金屬桿不同組合形式，能夠實現保護沖擊端或者支撐端的功能。D.Karagiozova等[9]對比高速沖擊下多胞材料中沖擊波傳播的距離，認為密度梯度多胞材料與均勻密度多胞材料相比在能量吸收方面沒有明顯優勢。

多胞金屬是理想的吸能材料，常用于抗爆炸夾芯結構的芯層。如果多胞犧牲層的芯層厚度設計得過大，吸收完爆炸能量后仍有未利用的區域；如果太小，材料完全壓實，沖擊波在支撐端反射后，出現應力增強現象。因此，對芯層厚度進行優化設計以充分發揮其吸能能力顯得極為重要。在工程應用中，最常見的是單層單一密度犧牲層，A.G.Hanssen等[10]基于剛性-理想塑性-鎖定(rigid,perfectly-plastic,locking,R-PP-L)模型[1]，給出了近距離爆炸載荷作用下芯層最小厚度的理論解。G.W.Ma等[11]引入雙層密度犧牲層到抗爆結構中，發現低密度泡沫靠近爆炸端、高密度泡沫靠近支撐端的構型可以吸收更多的能量，但是主體結構承受應力較大。采用與之相反的構型，Liao Shenfei等[12]達到了降低支撐端應力的目標，給出了臨界厚度的設計方法。丁圓圓等[13]基于更精確的剛性-塑性硬化(rigid-plastic hardening, R-PH)模型[14]揭示了均勻密度多胞犧牲層中沖擊波的傳播規律。因此，改變密度的分布可以滿足更多的設計需求。

本文中，選用密度線性分布的梯度多胞金屬作為芯層材料，在相同爆炸載荷下，以芯層材料所需要的臨界厚度和支撐端應力峰值為指標，根據沖擊波在密度梯度多胞金屬中的傳播規律和犧牲層的響應特性，考察不同梯度多胞金屬吸能的優劣，以期為工程防護設計提供參考。

1 理論模型

1.1 問題描述

當爆炸源到犧牲層的距離遠大于被保護結構的尺寸時，爆炸載荷產生的球面波可以近似為平面波[15]。最早由Taylor發展了爆炸脈沖入射到自由面上的一維沖擊波理論，單位面積上的爆炸載荷可以假設為一個指數衰減波，形如：

(1)

式中：t為時間，p0為初始峰值載荷，τ為衰減時間常數，易見爆炸載荷的沖量為p0τ。

以密度梯度多胞金屬材料為芯層，在爆炸載荷作用方向上密度漸進增加的稱為正梯度犧牲層，反之則稱為負梯度犧牲層，見圖1。本文中選用密度沿加載方向線性分布的多胞金屬，其相對密度分布：

(2)

式中：γ為密度梯度參數，ρ0為平均相對密度，L0為芯層X方向上的厚度。γ取值的正、負分別對應于正、負梯度材料。多胞犧牲層的覆蓋層假設為剛性質量塊，面積質量記為m，支撐端視為固定的。

多胞金屬的壓縮行為包含3個階段：彈性、平臺和壓實段。R-PP-L模型廣泛應用于描述多胞材料的應力應變關系，以此發展了一維沖擊波理論[16]以研究多胞金屬的動態響應。然而，R-PP-L模型高估了材料的壓潰應力和能量吸收能力。Zheng Zhijun等[14]提出了率無關的R-PH模型以表征均勻泡沫金屬材料在準靜態壓縮下的力學行為，其應力應變關系可以寫作:

(3)

式中:初始壓潰應力σ0、應變硬化參數C都是與相對密度有關的量[17]。

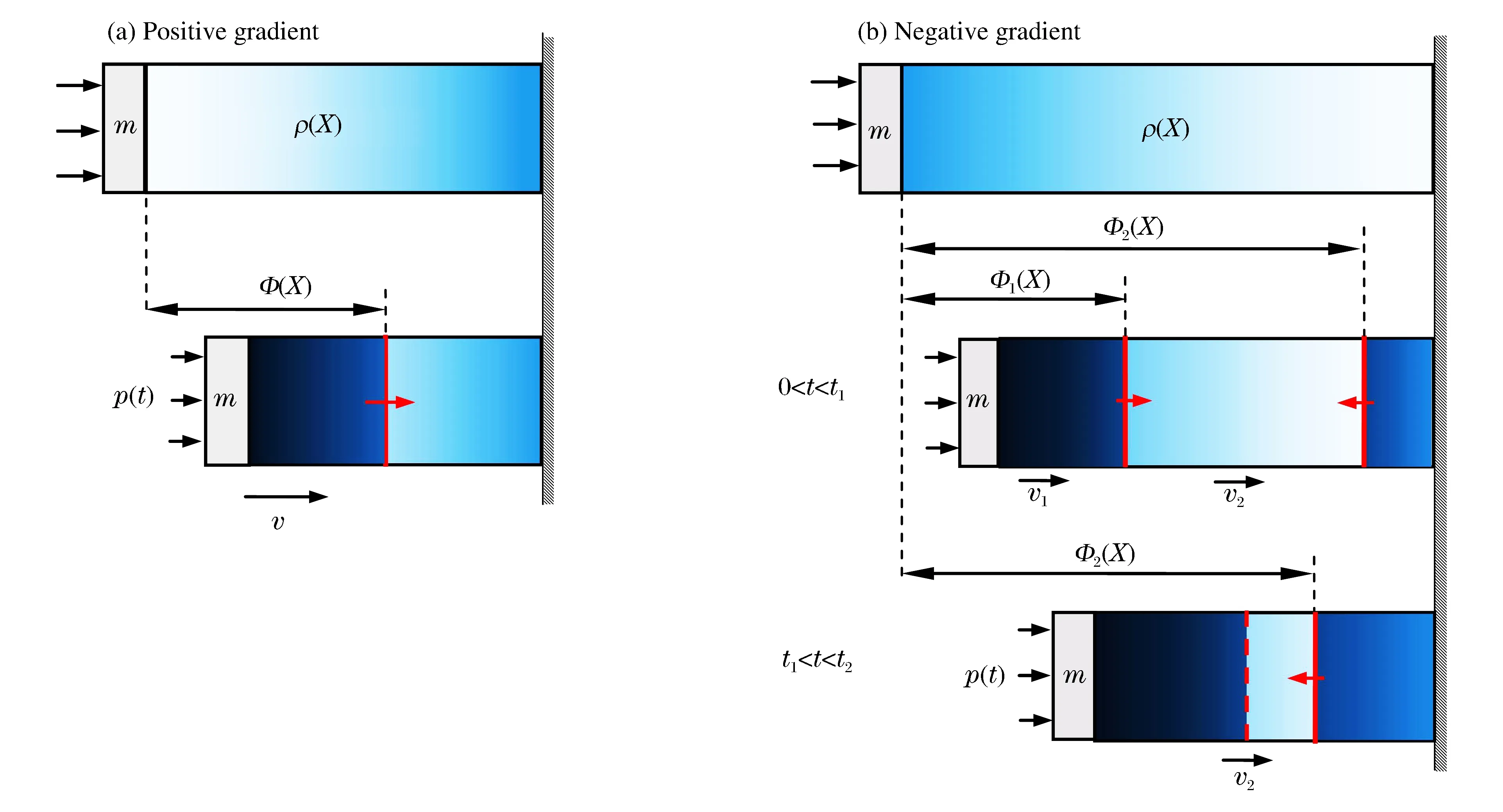
圖1 梯度多胞犧牲層的抗爆炸示意圖Fig.1 Schematic diagrams for the anti-blast analysis of graded cellular sacrificial claddings

1.2 正梯度犧牲層的抗爆炸分析模型

在爆炸載荷作用下，正梯度多胞金屬中沖擊波傳播的理論分析模型如圖1(a)所示。在初始構形中建立坐標系，沖擊波陣面的Lagrange坐標為Φ(t)。根據R-PH模型假定，當犧牲層承受到爆炸載荷時，彈性前驅波在沖擊端產生并以無窮大的速度向支撐端傳播，同時沖擊波也在沖擊端產生并以其特定的速度向前傳播，當塑性沖擊波掃過某個位置時，質點速度、應變和應力從波前的{0,0,σ0(ρ(Φ))}突變為波后的{v(t),εb(t),σb(t)}，其中v為速度，σ0(ρ(Φ))為當地的初始壓潰應力。

由應力波理論，跨過沖擊波陣面的質量守恒和動量守恒分別給出:

(4)

(5)

式中:ρs為基體材料密度。聯立可得波后應力為:

(6)

另外，聯立式(3)和(6)可以求出波后應變:

(7)

進一步考察覆蓋層和沖擊波波后區域組成的部分，由牛頓運動定律，有:

(8)

結合上述方程，可以得到控制方程:

(9)

初始條件為Φ(0)=0和v(0)=0。這是非線性微分方程組，沒有顯式解，因此本文中采用四階Runge-Kutta法進行數值求解。為了獲得犧牲層的臨界厚度Lc，先給定一個足夠大的厚度L0，若沖擊波停止的位置不在支撐端，則調整L0的值，直至沖擊波停止的位置正好在支撐端，此時的L0即為臨界厚度。

1.3 負梯度犧牲層的抗爆炸分析模型

多胞金屬在壓潰過程中，一旦局部應力達到當地的屈服強度就會產生局部變形。對于負梯度犧牲層，沖擊端的應力急劇上升而發生逐層壓潰[18]，而不同于正梯度情形，支撐端也會出現沖擊波且朝著相反的方向傳播，如圖1(b)所示。這是由于多胞金屬密度低的位置強度低，負梯度犧牲層強度在沖擊方向上遞減。所以，支撐端達到當地初始壓潰應力后出現坍塌并逐漸向強度高的地方擴展，可以看成一個向沖擊端傳播的塑性壓縮波。在負梯度犧牲層中形成了雙波結構，分別記為Shock 1和Shock 2。這2個波陣面把犧牲層分成3部分：第1部分是質量塊到Shock 1緊后方區域，在爆炸加載下速度急劇上升，之后隨著波后應力增大而不斷減速，速度記為v1；第2部分是中間未變形區域，在其左右兩端的波前應力差作用下，v2由0開始增加到與第1部分速度相同，最后減速直至犧牲層運動停止；第3部分為支撐端到Shock 2波后的材料，速度為0。

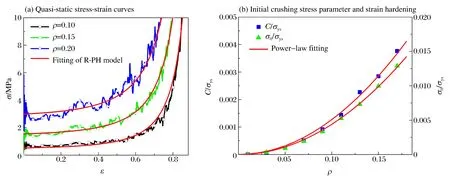
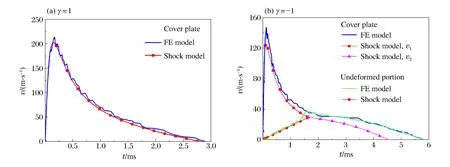
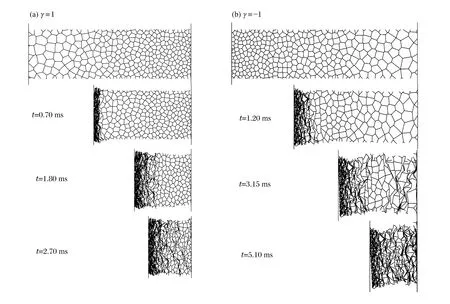
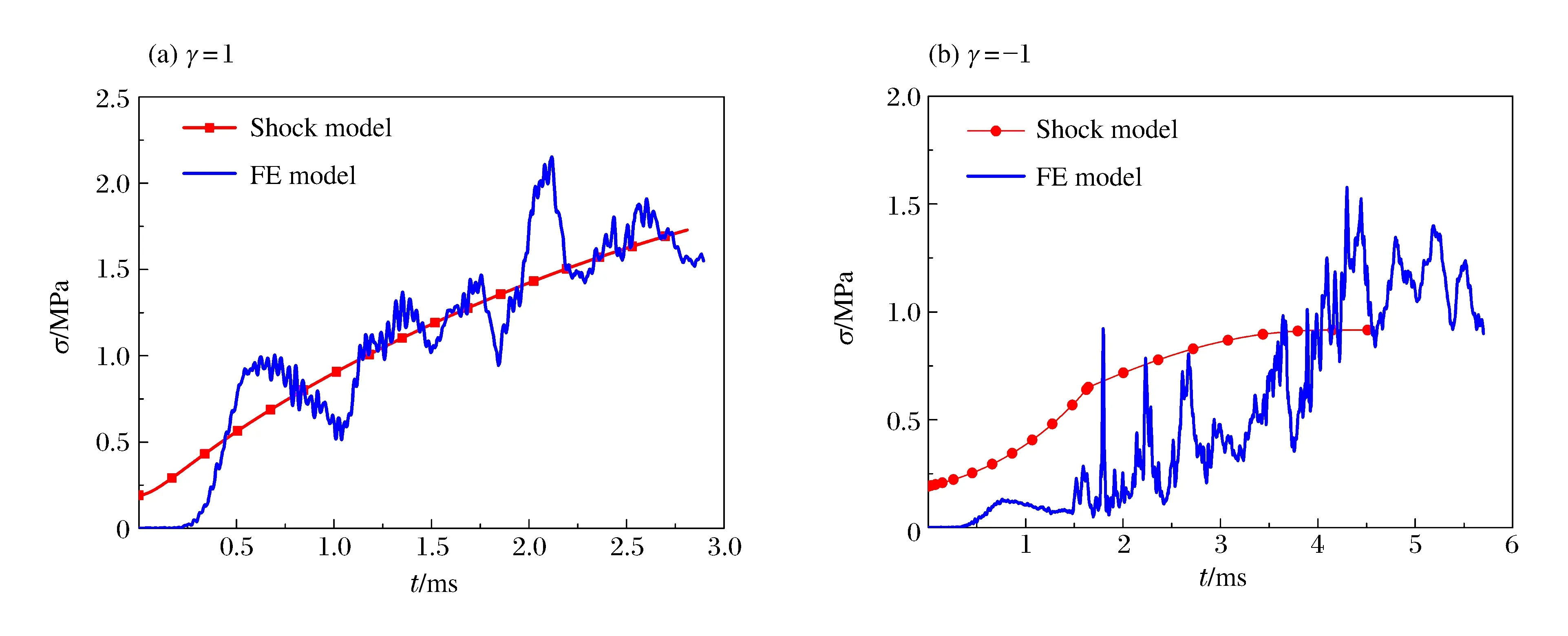
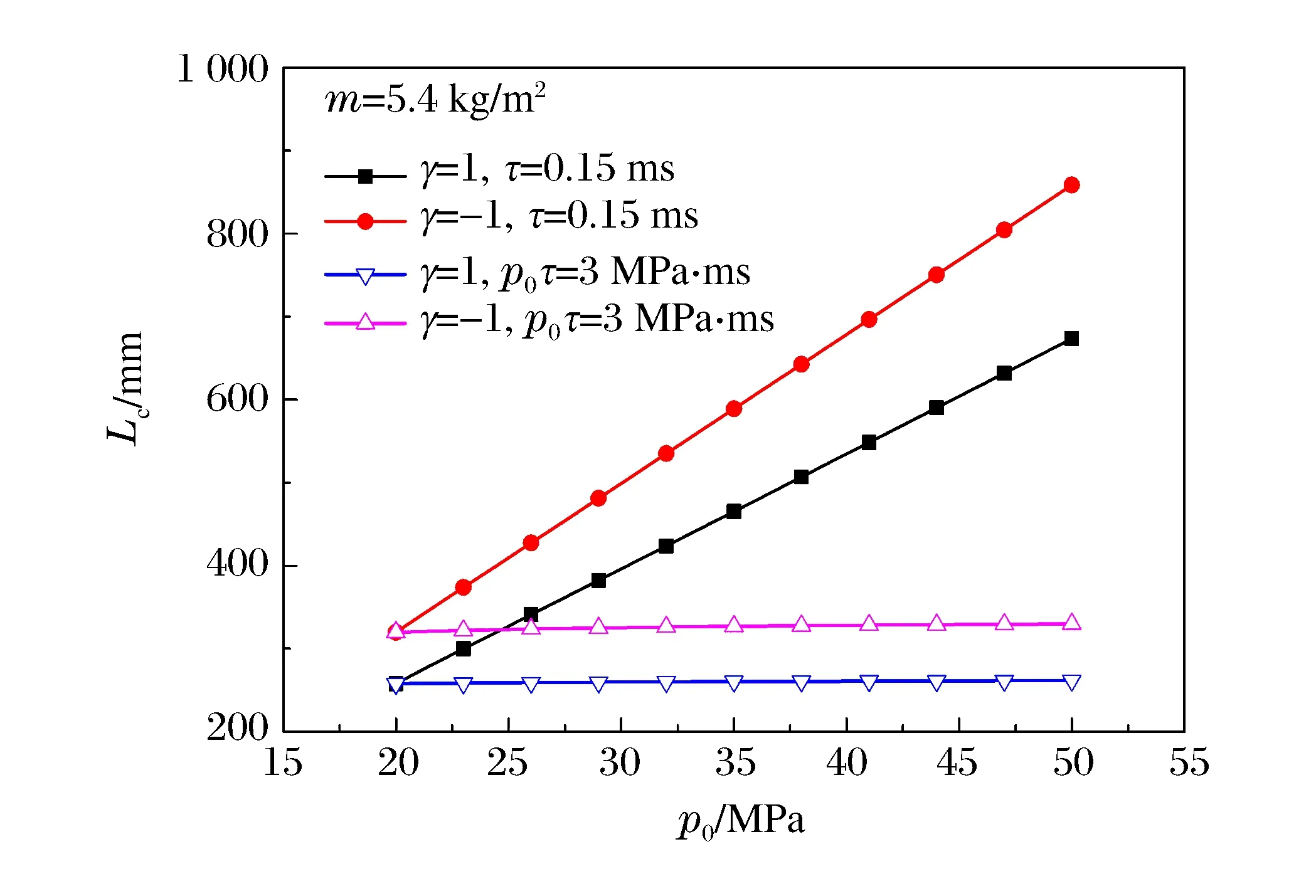
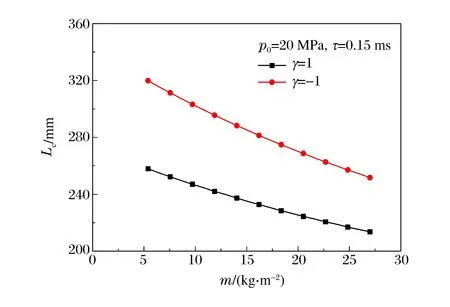
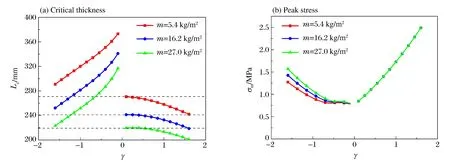
第1階段：0

(10)

而初始條件為Φ1(0)=0,v1(0)=0,Φ2(0)=L0以及v2(0)=0。

第2階段：t1

(11)

而定解條件由第1階段結束時給出。同樣采用四階Runge-Kutta法進行數值求解。

根據該理論模型，首先給定L0一個足夠大的初值進行響應分析，若運動停止時犧牲層仍然有未變形區域，則調整L0的值重新計算，直至運動結束時Shock 2的Lagrange坐標與運動第1階段Shock 1停止的位置重合，犧牲層得到了充分利用，此時選定的厚度L0即為臨界厚度Lc。

2 細觀有限元模型

考察具有不同相對密度的二維均勻Voronoi蜂窩[19]在準靜態壓縮下的力學行為，如圖2(a)所示。基體材料密度ρs為2 700 kg/m3，材料滿足彈性-理想塑性假定，楊氏模量為69 GPa，泊松比為0.3，屈服強度為175 MPa。通過R-PH模型對名義應力應變曲線進行擬合，可以確定其參數隨相對密度的變化特征。結果表明，初始壓潰應力σ0和硬化參數C與相對密度近似呈二次方關系，如圖2(b)所示，擬合關系為：

(12)

式中：σys為基體材料的屈服應力。

圖2 不同相對密度Voronoi蜂窩的準靜態應力應變曲線和初始壓潰應力和硬化參數的擬合結果Fig.2 Quasi-static stress-strain curves and fitting results of initial crushing stress parameter and strain hardening for Voronoi honeycombs with different relative densities

利用二維隨機Voronoi技術[19]和變胞元尺寸分布法[5]構建密度梯度多胞金屬的細觀有限元模型。固定胞壁厚度h0為0.26 mm，樣本不規則度k取0.4，生成梯度Voronoi蜂窩的平均相對密度ρ0= 0.1。運用ABAQUS/Explicit進行數值模擬，胞壁選用S4R殼單元，基體材料性質同上所述。數值模擬情形為平面應變狀態，即所有節點在面外方向上的位移限制為零，并且通過施加幾何約束使得在前后2個面上的對應節點在面內的運動保持一致，以避免殼單元在面外方向上發生扭曲。通過網格收斂性分析，單元的平均長度約為0.5 mm。所有接觸面定義為通用接觸，摩擦因數取為0.2。正、負梯度模型寬度均為80 mm，厚度方向取1 mm，長度取為理論模型得到的臨界厚度，分別為257.9和320.0 mm。抗爆炸密度梯度多胞犧牲層的有限元模型如圖3所示。右端為靜止的剛性壁面，左端覆蓋剛性質量塊，外表面作用指數型爆炸載荷，上下邊界為自由邊界。

圖3 抗爆炸密度梯度多胞犧牲層的細觀有限元模型Fig.3 Cell-based finite element (FE) models of graded cellular sacrificial claddings for blast mitigation

3 結果與討論

3.1 理論結果與有限元結果的比較

本節中爆炸載荷參數p0=20 MPa，τ=0.15 ms，覆蓋層m=5.4 kg/m2，多胞金屬平均相對密度為ρ0=0.1。

正、負梯度犧牲層波后質點速度歷史曲線如圖4所示。正梯度犧牲層沖擊端速度在很短的時間內達到最大值，隨后開始迅速下降，最后較緩慢地減小。臨界厚度為爆炸能量恰好被犧牲層吸收時多胞芯層的最小厚度，即為沖擊波掃過的距離。經歷響應時間tm=2.8 ms，犧牲層速度降為零。由圖可見，沖擊波理論模型預測結果與有限元計算結果吻合很好。沖擊波傳到的位置恰好為支撐端，以此設計出的臨界厚度Lc=257.9 mm。負梯度犧牲層的響應比較復雜，中間未變形區域從靜止開始加速運動，與沖擊端獲得共同速度后緩慢地下降為零。在第2階段Shock 2到達Shock 1停止的位置，若恰好爆炸能量完全被吸收，設計出的臨界厚度Lc=320.0 mm，最終時刻tm=4.5 ms。由圖可見，理論預測與有限元計算結果吻合較好，但有限元模型得到的響應時間要比理論模型得到的響應時間長。爆炸載荷作用的初始階段，沖擊端處速度高，兩者都能觀察到連續的塑性壓潰面。正梯度犧牲層很規整地逐層坍塌，而負梯度犧牲層的壓潰面密實程度相對較低，后續的壓潰區域逐漸變得松散，表現出了變形局部化的特點。特別地，負梯度靠近支撐端附近可以明顯地觀察到胞元變形，起初并未完全坍塌閉合，隨著中間區域沖擊速度由零開始不斷增大，支撐端附近產生隨機剪切帶[14]，說明了壓縮波產生于支撐端附近。后期，沖擊速度不斷衰減，正梯度犧牲層靠近沖擊端也出現類似的變形模式，如圖5所示。

圖4 速度歷史曲線Fig.4 Time history of velocity

隨著爆炸載荷的作用，正梯度犧牲層由于其高密度端靠近被保護結構，支撐端應力隨著沖擊波陣面上透射波的增強而增強；而負梯度犧牲層支撐端應力由Shock 2波后應力確定，如圖6所示。正梯度吻合較好，負梯度理論預測的支撐端應力變化趨勢與有限元計算結果一致，但是應力值偏大。主要是由于理論模型采用連續體假設，認為在響應的起始階段支撐端立刻出現塑性沖擊波，而Voronoi模型表現為胞棱彎曲變形且胞元未完全坍塌壓實，因此理論解高估了支撐端應力。如果支撐端應力不大于許可應力，這種基于臨界厚度的抗爆炸設計便是有效的。

圖5 變形圖Fig.5 Deformation patterns

圖6 支撐端應力的歷史曲線Fig.6 Time history of stress at the support end

圖7 臨界厚度隨初始加載峰值的變化Fig.7 Critical thickness versus peak pressure of blast load

圖8 臨界厚度隨覆蓋層面積質量的變化關系Fig.8 Critical thickness versus area mass of cover plate

3.2 臨界厚度的影響參數分析

本節運用理論模型分析爆炸載荷強度、覆蓋層質量以及密度梯度變化對犧牲層臨界厚度的影響，為工程設計提供參考。

首先對于給定的密度梯度犧牲層，考察爆炸載荷對臨界厚度的影響，如圖7所示。結果表明在爆炸沖量p0τ保持不變時，臨界厚度Lc幾乎不變；而當τ保持不變時，Lc隨著爆炸初始峰值近似地呈線性增加。同樣地，保持p0不變，Lc隨τ也會有類似的變化關系。由此可知，爆炸載荷是以沖量p0τ的形式影響Lc的大小。

其次，考慮梯度多胞犧牲層吸收相同爆炸載荷時，臨界厚度隨覆蓋層質量的變化規律。結果表明，臨界厚度隨著覆蓋層質量增大而減小，如圖8所示。這是由于爆炸載荷是以沖量形式加載的，覆蓋層質量的大小決定了爆炸載荷轉化為動能的能力，即質量越大，由爆炸載荷所做的功越小。在設計允許范圍內，增大覆蓋層質量是有利的。

最后，考察密度梯度參數γ對多胞犧牲層臨界厚度的影響。由于使用了相同的平均相對密度的芯層，因此吸收同等強度的爆炸能量下，犧牲層臨界厚度的大小直接反映需要材料的多少,如圖9所示。

在圖9(a)中，虛線對應于均勻密度多胞芯層的臨界厚度。顯然，正梯度芯層需要的厚度小于均勻密度多胞芯層的臨界厚度，而負梯度芯層臨界厚度相對較大。在工程上選用正梯度可以設計出更薄、更輕的犧牲層。另外，γ表征了密度分布的陡峭程度，隨著其絕對值的增加，材料局部密度的差異增大。正、負梯度犧牲層的臨界厚度都隨著|γ|的增大而減小，因此選取更大的密度梯度參數絕對值，對于減小芯層厚度也是有利的。

圖9 臨界厚度和支撐端應力峰值隨密度梯度參數的變化Fig.9 Variations of critical thickness and peak stress at the support end with the gradient parameter

支撐端應力峰值σm隨γ的變化關系如圖9(b)所示。對于相同的|γ|，選用正梯度芯層帶來的應力峰值更大。正梯度芯層應力峰值出現在響應結束時刻，即沖擊波運動至支撐端、應力達到密度最大位置對應的初始壓潰應力，它和覆蓋層質量的選取無關并且與γ近似呈二次方關系。負梯度多胞芯層的應力峰值為沖擊波波后應力的最大值，與不同運動階段的響應有關。隨著|γ|增大，應力峰值起初維持在很低的水平，當|γ|大于某個特定值之后，應力峰值逐漸上升，例如m取5.4 kg/m2時，應力峰值為0.53 MPa。同時，覆蓋層對負梯度芯層的支撐端應力也有影響，質量越大，應力峰值越大。

進一步分析可知，支撐端應力峰值和臨界厚度這2個設計指標之間呈負相關，即在工程設計中要獲得較低的應力峰值必然要增加芯層厚度。如果希望被保護結構承受應力最小，選用|γ|較小的負梯度或者均勻密度效果更好，在受限的空間下，均勻密度多胞芯層最優。當給定覆蓋層質量并限定支撐端應力峰值時，選擇適當的正梯度參數可得到最小的犧牲層厚度。因此，圖9可為密度梯度多胞犧牲層的抗爆炸設計提供依據。

4 結 論

研究了密度梯度多胞犧牲層的抗爆炸性能，采用率無關的剛性-塑性硬化模型描述多胞金屬材料的應力應變關系，對于正梯度和負梯度情形分別建立了一維非線性塑性沖擊波模型，揭示了塑性沖擊波在梯度多胞金屬中的傳播規律，得到了梯度多胞犧牲層的響應特性，進而給出了芯層臨界厚度的設計方法。考慮爆炸載荷強度、覆蓋層質量和密度梯度參數對臨界厚度的影響，發現可以通過增大覆蓋層質量和密度梯度參數設計出更小的臨界厚度。以臨界厚度和支撐端應力峰值為指標，對比不同梯度多胞金屬吸收相同爆炸載荷能力的優劣。結果表明，通過增大梯度參數值，正梯度能夠有效地降低芯層厚度，但是會帶來支撐端應力峰值的增大；如果要實現應力峰值最小，同時考慮盡可能小的厚度，均勻密度是較理想的選擇。采用細觀有限元模型檢驗了犧牲層抗爆炸分析的可靠性，理論預測結果與有限元結果吻合較好，說明基于非線性塑性硬化沖擊波模型設計梯度多胞犧牲層是有效的。

[1] Reid S R, Peng C. Dynamic uniaxial crushing of wood[J]. International Journal of Impact Engineering, 1997,19(5/6):531-570.

[2] Liu Jiagui, Hou Bing, Lu Fangyun, et al. A theoretical study of shock front propagation in the density graded cellular rods[J]. International Journal of Impact Engineering, 2015,80:133-142.

[3] Guruprasad S, Mukherjee A. Layered sacrificial claddings under blast loading: Part I: Analytical studies[J]. International Journal of Impact Engineering, 2000,24(9):957-973.

[4] Cui L, Kiernan S, Gilchrist M D. Designing the energy absorption capacity of functionally graded foam materials[J]. Materials Science and Engineering A, 2009,507(1):215-225.

[5] Zhang Jianjun, Wang Zhihua, Zhao Longmao. Dynamic response of functionally graded cellular materials based on the Voronoi model[J]. Composites Part B: Engineering, 2016,85:176-187.

[6] 吳鶴翔,劉穎.梯度變化對密度梯度蜂窩材料力學性能的影響[J].爆炸與沖擊,2013,33(2):163-168. Wu Hexiang, Liu Ying. Influences of density gradient variation on mechanical performances of density graded honeycomb materials[J]. Explosion and Shock Waves, 2013,33(2):163-168.

[7] Wang Xiaohai, Zheng Zhijun, Yu Jilin. Crashworthiness design of density-graded cellular metals[J]. Theoretical and Applied Mechanics Letters, 2013,3(3):9-13.

[8] Zheng Jie, Qin Qinghua, Wang T J. Impact plastic crushing and design of density-graded cellular materials[J]. Mechanics of Material, 2016,94:66-78.

[9] Karagiozova D, Alves M. Propagation of compaction waves in cellular materials with continuously varying density[J]. International Journal of Solids and Structures, 2015,71:323-337.

[10] Hanssen A G, Enstock L, Langseth M. Close-range blast loading of aluminum foam panels[J]. International Journal of Impact Engineering, 2002,27(6):593-618.

[11] Ma G W, Ye Z Q. Energy absorption of double-layer foam cladding for blast alleviation[J]. International Journal of Impact Engineering, 2007,34(2):329-347.

[12] Liao Shenfei, Zheng Zhijun, Yu Jilin, et al. A design guide of double-layer cellular claddings for blast alleviation[J]. International Journal of Aerospace and Lightweight Structures, 2013,3(1):109-133.

[13] Sawle D R. Hypervelocity impact in thin sheets, semi-infinite targets at 15 km/s[J]. AIAA Journal, 1970,8(7):1240-1244.

[14] 丁圓圓,王士龍,鄭志軍,等.多胞犧牲層的抗爆炸分析[J].力學學報,2014,46(6):825-833. Ding Yuanyuan, Wang Shilong, Zheng Zhijun, et al. Anti-blast analysis of cellular sacrificial cladding[J]. Chinese Journal of Theoretical and Applied Mechanics, 2014,46(6):825-833.

[15] Fleck N A, Deshpande V S. The resistance of clamped sandwich beams to shock loading[J]. Journal of Applied Mechanics, 2004,71(3):386-401.

[16] Tan P J, Reid S R, Harrigan J J, et al. Dynamic compressive strength properties of aluminium foams: Part II: Shock theory and comparison with experimental data and numerical models[J]. Journal of the Mechanics and Physics of Solids, 2005,53(10):2206-2230.

[17] Wang Shilong, Ding Yuanyuan, Wang Changfeng, et al. Dynamic material parameters of closed-cell foams under high-velocity impact[J]. International Journal of Impact Engineering, 2017,99:111-121.

[18] 王長峰,鄭志軍,虞吉林.泡沫桿撞擊剛性壁的動態壓潰模型[J].爆炸與沖擊,2013,33(6):587-593. Wang Changfeng, Zheng Zhijun, Yu Jilin. Dynamic crushing models for a foam rod striking a rigid wall[J]. Explosion and Shock Waves, 2013,33(6):587-593.

[19] Zheng Zhijun, Yu Jilin, Li Jianrong. Dynamic crushing of 2D cellular structures: A finite element study[J]. International Journal of Impact Engineering, 2005,32(1/2/3/4):650-664.

(責任編輯 張凌云)

Anti-blast analysis of graded cellular sacrificial cladding

Cai Zhengyu1, Ding Yuanyuan2, Wang Shilong1, Zheng Zhijun1, Yu Jilin1

(1.CASKeyLaboratoryofMechanicalBehaviorandDesignofMaterials,DepartmentofModernMechanics,UniversityofScienceandTechnologyofChina,Hefei230026,Anhui,China;2.MechanicsandMaterialsScienceResearchCenter,NingboUniversity,Ningbo315211,Zhejiang,China)

The blast mitigation behavior of a density-graded cellular sacrificial cladding is investigated by using a nonlinear plastic shock model and a cell-based finite element model. Based on a rate-independent, rigid-plastic hardening idealization, a theoretical approach is applied to analyze the propagation of shock wave in density-graded cellular rods subjected to blast loading. The influences of the intensity of blast load, the cover mass and the density gradient parameter of the cellular material on the critical thickness, which is the minimum thickness of the core layer when the energy of explosion is fully absorbed, are investigated. A design guide of density-gradient is provided which considers the critical thickness of the cellular core as well as the peak stress at the support end. The validity of the anti-blast analysis of the graded cellular sacrificial cladding based on the nonlinear plastic shock model is verified by using cell-based finite element models.

cellular materials; sacrificial cladding; blast load; shock wave; finite element method

10.11883/1001-1455(2017)03-0396-09

2017-02-20；

2017-04-28

國家自然科學基金項目(11372307,11372308)

蔡正宇(1990— )，男，碩士研究生; 通信作者: 鄭志軍，zjzheng@ustc.edu.cn。

O382 國標學科代碼： 13035

A