考慮自動駕駛儀動態特性和攻擊角約束的魯棒末制導律

楊靖， 王旭剛， 王中原, 常思江

(南京理工大學 能源與動力工程學院, 江蘇 南京 210094)

?

考慮自動駕駛儀動態特性和攻擊角約束的魯棒末制導律

楊靖， 王旭剛， 王中原, 常思江

(南京理工大學 能源與動力工程學院, 江蘇 南京 210094)

針對制導彈箭打擊機動目標時帶攻擊角約束的末制導問題，考慮自動駕駛儀動態特性以及目標機動不確定性對制導過程的影響，結合積分滑模與動態面控制方法，設計了一種新型魯棒末制導律。自動駕駛儀的動態特性以含擾動的2階動力學模型來表征，目標機動引起的模型不確定性以光滑非線性擾動觀測器來估計。滑模面取視線角速率與視線角偏差的組合形式，且引入剩余飛行時間，以使制導彈箭在整個末制導過程中過載性能良好。依據李雅普諾夫穩定性理論證明了閉環系統中視線角速率與視線角偏差均最終一致有界任意小。通過數值仿真與彈道成型制導律及非奇異滑模制導律進行了對比，驗證了該末制導律的有效性與優越性。

兵器科學與技術； 末制導律； 攻擊角約束； 積分滑模； 動態面控制； 擾動觀測器

0 引言

火炮武器系統在戰場中反應迅速，能夠提供強大且持續的火力支援，是未來部隊聯合作戰的重要組成單元。隨著現代戰爭理念的發展，遠程壓制、精確打擊及高效毀傷等成為適配彈箭的發展方向。在一些實際應用中(如反坦克、反艦船及近程反導等)，若制導彈箭能以一定的攻擊角度命中目標，可以充分發揮其戰斗部威力，提高殺傷效果，同時也降低了戰爭成本。因此，研究制導彈箭帶攻擊角約束的精確末制導問題具有重要的現實意義。

自從Kim等[1]針對再入式飛行器首次提出帶攻擊角約束的最優末制導律以來，很多學者針對不同研究對象，開展了帶攻擊角約束的末制導律研究。總的來說，分為兩大類：1)假設目標機動已知，依據不同的性能指標，設計含攻擊角約束的最優末制導律[2-5]；2)將目標機動視為外部擾動，研究含攻擊角約束的魯棒末制導律[6-13]。

在應用最優控制理論的設計中，通常將含攻擊角約束的末制導律問題轉化為線性二次型最優控制問題，從而可得到解析形式的最優制導律。Zarchan[2]證明了在彈目速率不變、目標常值機動、制導系統無動力學滯后的條件下，使得脫靶量為0 m，且需用過載平方積分最小的制導律為彈道成型制導律(TSG)。此外，其引入零控脫靶量的概念，闡述了偏置比例制導律[3-4]與彈道成型制導律本質上是一致的。張友安等[5]針對固定目標，考慮彈體1階動力學滯后，設計了一種帶攻擊角約束的最優末制導律。Cho等[6]針對以一定攻擊角打擊任意機動目標的情形，引入零控碰撞三角形，將平面內非線性彈目相對運動模型線性化，設計了一種新型含攻擊角約束的最優末制導律。該方法仍需要目標的狀態信息完全已知，但是在實際應用中，很多的目標狀態無法準確測得，從而其應用受到限制。

在含攻擊角約束的魯棒末制導律設計中，通常將目標機動視為外部擾動，期望閉環系統對目標機動等因素引起的模型不確定性具有很好的穩定性與魯棒性。作為魯棒控制方法的一種，滑模控制具有對內部或外界的匹配擾動不敏感、控制精度高且算法簡單、易于實現等特點，應用較為廣泛。Rao等[7]將視線角速率偏差與視線角偏差的線性組合作為滑模面，設計了一種含攻擊角約束的滑模末制導律。Kumar等[8]以視線角速率偏差與視線角偏差構建了一種非奇異滑模面，設計了一種含攻擊角約束的有限時間收斂的非奇異滑模末制導律。上述方法都存在初始過載飽和的現象，這對內環自動駕駛儀提出了較高的要求。當自動駕駛儀回路帶寬不夠高的情況下，制導性能受到很大影響。因此，有必要在設計含攻擊角約束的制導律中考慮內回路自動駕駛儀的動態特性。

當考慮內回路自動駕駛儀的動態特性，會使得整個系統的階次較高，反步法適合處理該問題。反步法是一種遞推設計方法，可以將高階系統的控制律設計問題轉化為對一系列低階系統的交互設計。刁兆師等[9]將自動駕駛儀回路視為1階動力學滯后，針對地面固定目標，應用反步法設計了一種帶攻擊角約束的末制導律。He等[10]引入線性阻尼，以視線角速率偏差與視線角偏差構建了一種非奇異滑模面，將自動駕駛儀回路視為2階動力學環節，利用反步法設計了一種含攻擊角約束的末制導律。但是，反步法中存在多次反步時“微分膨脹”的問題。

為了解決多次反步設計出現的“微分膨脹”問題，Swaroop等[11]結合非線性阻尼、積分反步及多面滑模控制的優點，提出了動態面控制方法。該方法不僅避免了反步設計中的“微分膨脹”問題，且不需要系統擾動項滿足利普希茨連續條件。熊少鋒等[12]以視線角速率偏差與視線角偏差構建了一種非奇異滑模面，將自動駕駛儀近似為1階慣性環節，采用非奇異滑模與動態面控制方法，設計了一種含攻擊角約束的末制導律。張堯等[13]引入非線性飽和函數及非線性阻尼，構建了一種新型積分型滑模面，將自動駕駛儀回路近似為2階動力學環節，采用動態面控制方法，設計了一種含攻擊角約束的新型末制導律。積分型滑模可使得系統從一開始就處于滑動模態，從而整個過程中不受擾動的影響。但是上述設計都未考慮自動駕駛儀模型的不確定性。

鴨式布局的制導彈箭為最小相位系統。因此，將其內回路自動駕駛儀的動態特性描述為含擾動的2階動力學過程更為合理。

基于上述考慮，本文以含擾動的2階動力學過程表征內回路自動駕駛儀的動態特性，結合積分滑模與動態面控制方法，設計了一種新型魯棒末制導律，即積分滑模動態面控制末制導律(ISMDSG)。受彈道成型制導律的啟發，在滑模變量的定義中引入剩余飛行時間，來改善整個末制導過程中的過載性能。采用擾動觀測器補償目標機動以及彈目速率變化引起的模型不確定性的影響。依據Lyapunov穩定性理論證明了視線角速率與視線角偏差均最終一致有界任意小，即實現了以一定的攻擊角命中目標。

1 問題描述

1.1 平面內彈目相對運動模型

假設制導彈箭為軸對稱外形，具有滾轉穩定系統，采用側滑轉彎機動模式。因而，可實現三通道解耦，僅考慮縱向平面內的運動。縱向平面內的彈目相對運動關系如圖1所示。

圖1 平面內彈目相對運動關系Fig.1 Projectile-target relative movement in plane

圖1中，Oxy為地面參考慣性坐標系；R為彈目相對距離；λ為彈目視線角；v、θ、a分別表示速度、彈道傾角和加速度；末端攻擊角θimp定義為制導彈箭末端速度vPf與目標末端速度vTf之間的夾角。可得縱向平面內的彈目相對運動關系

(1)

對(1)式中的第2式求時間的導數，結合(1)式中的其他各式，可得視線角速率的動力學模型：

(2)

h=aP(1-cos(θP-λ))+aTcos(θT-λ)-

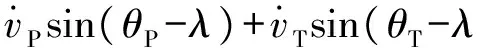
(3)

由此可知，h含目標機動及目標速度變化引起的擾動。

1.2 自動駕駛儀模型

實際中，外環制導回路生成的加速度指令是通過內環自動駕駛儀實現的。考慮到高頻未建模動態的影響，自動駕駛儀的帶寬不能過高。加速度指令與實際加速度之間總是存在一定的動力學滯后，這種時間延遲勢必影響制導性能。因而，設計末制導律時，有必要考慮自動駕駛儀的動態特性。對于鴨式布局的制導彈箭，自動駕駛儀回路作為制導回路的一個環節，其動態特性可用含擾動項的2階動力學近似表征：

(4)

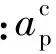
1.3 機動目標模型

假設目標可由1階動力學模型描述：

(5)

1.4 制導策略

Kumar等[7]的研究表明：不失一般性，假設目標末端速度傾角θTf=0，則當彈目位于碰撞三角形上時，末端視線角λf與攻擊角θimp存在一一對應關系：

(6)

式中：vT/vP<1.

因此，前述制導律設計目標等價于：

(7)

2 ISMDSG設計

2.1 制導律設計

為了使得末制導過程中的過載特性較為良好，類比彈道成型制導律，引入剩余飛行時間tgo，定義新變量s為

(8)

σ=s+z,z(0)=-s(0),

(9)

式中：輔助變量z滿足

(10)

k為設計參數。

對(9)式求導，結合(2)式，整理得

(11)

(12)

最終目標為設計控制輸入u，使得x1在有限時間內收斂到零點的任意小領域內。

動態面控制方法[12]結合了非線性阻尼、積分反步及多面滑模控制的優點，避免了反步設計中的“微分膨脹”問題，且不需要系統擾動項滿足Lipchitz條件。因此，采用動態面控制方法對(12)式描述的問題進行設計，具體步驟為：

1) 設計虛擬控制量x2d. 定義第1個動態面：

S1=x1,

(13)

為使S1漸近收斂到零點附近，設計虛擬控制量為

(14)

式中：τ2>0為設計參數；

(15)

2) 設計虛擬控制量x3d.定義第2個動態面：

S2=x2-x2d,

(16)

為使S2漸近收斂到零點附近，設計虛擬控制量為

(17)

式中：τ3>0為設計參數；

(18)

K2>0為設計參數。

3) 設計實際控制量u. 定義第3個動態面：

S3=x3-x3d,

(19)

為使S3漸近收斂到零點附近，設計實際控制量為

(20)

式中：K3>0、ε3>0為設計參數；ρ3≥|da|.

2.2 穩定性分析

定義新的變量為

(21)

結合動態面Si,i=1,2,3的定義與(21)式，可得

(22)

對(13)式中的S1求導，并將(22)式第2式與(15)式代入其中，整理得

(23)

對(16)式中的S2求導，并將(22)式第3式與(18)式代入其中，整理得

(24)

對(19)式中的S3求導，并將(20)式與(17)式代入其中，整理得

(25)

對(21)式中的y2求導，結合(21)式與(14)式，整理得

(26)

對(21)式中的y3求導，結合(21)式與(17)式，整理得

(27)

由Young不等式，可得

(28)

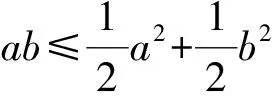
(29)

考慮到現實情況，(1)式中的相關參數及其導數都有界，即存在M2、M3滿足

(30)

由此可得

(31)

定義Lyapunov函數為

(32)

對(32)式求導，結合(29)式與(31)式，可得

(33)

選取參數K1、K2、K3、τ2、τ3滿足：

(34)

式中：κ>0.

從而，有

(35)

(36)

依據比較原理，有

(37)

由此可見，S1、S2、S3、y2、y3是一致最終有界的。當κ足夠大時，VL很快收斂到域Ω={VL≤ζ/κ}。這也意味著視線角速率與末端視線角偏差可以足夠小。

綜上所述，可得如下定理。

2.3 估計不確定項h

(12)式中含有不確定項h，可采用光滑非線性擾動觀測器[15-16]獲得。為保持本文的完整性，以下首先簡述其要點，然后設計適用于本文問題的擾動觀測器。

考慮單輸入、單輸出系統

(38)

2階形式的光滑非線性擾動觀測器為

(39)

當ξ、η不存在測量噪聲時，z1在有限時間內收斂于f(t)；當ξ、η包含Lebesgue可測界為δ的噪聲時，z1在有限時間內收斂于f(t)的領域內，其精度為|z1(t)-f(t)|≤μδ2/3,μ>0.

對照(2)式的第1式，記

(40)

3 仿真分析

為了驗證本文所提出的ISMDSG的有效性與優越性，本節針對不同場景，做了大量仿真實驗，并與彈道成型制導律(TSG)[2]及非奇異滑模末制導律(NTSMG)[8]進行了仿真對比分析。由于篇幅所限，僅列出部分仿真結果。

對于固定或勻速直線運動的目標，TSG方法給出的過載指令為

(41)

NTSMG方法給出的過載指令為

(42)

(43)

對于機動目標，NTSMG方法給出的過載指令為

(44)

式中：λT=θT-λ. 假設所有用到的目標信息已知。

以下仿真場景中，3種制導律中的參數保持不變，假設制導彈箭與目標均處于鉛垂平面內。

3.1 情形1：目標固定

該仿真的目的是展示僅初始彈道傾角不同的情況下，要求垂直打擊固定目標時，采用ISMDSG方法的末制導性能。

設地面固定目標的坐標為xT=5 000 m，yT=0 m；制導彈箭的初始位置為xP0=0 m，yP0=8 660.3 m. 這意味著初始彈目距離為R0=10 km，初始彈目視線角為λ0=-60°. 假設制導彈箭的速度大小為常數，取vP=500 m/s；制導彈箭的最大法向過載設為40g；2階擾動近似自動駕駛儀模型中的參數為ξa=0.5，ωa=5 rad/s,其擾動項取為da=15sin (πt/3)；期望實現對地面固定目標的垂直攻頂。取末制導初始時刻的彈道傾角θP0分別為15°、0°、-15°、-30°、-45°、-60°進行仿真。

圖2～圖5分別展示了不同末制導初始彈道傾角的情況下，采用ISMDSG方法的末制導時，制導彈箭的運動軌跡、彈目視線角速率、彈目視線角與期望的視線角偏差值和彈體的方向過載變化。圖3表明彈目視線角速率在末端趨于0 °/s；圖4說明實際彈目視線角收斂于期望的末端視線角。從而，采用本文所提出的ISMDSG方法可以在不同初始彈道傾角時實現對固定目標的垂直打擊。從圖5可以看出，末制導初始時刻不同的彈道傾角情況下，末制導初始階段的法向過載差別較大，但最終的法向過載都趨于0g. 適當的末制導初始彈道傾角設計可降低末制導過程中的最大需要過載。

圖2 情形1：ISMDSG方法不同初始彈道傾角時 彈箭的運動軌跡Fig.2 Case 1: projectile trajectories at different initial flight path angles via ISMDSG

圖3 情形1：ISMDSG方法不同初始彈道傾角時 視線角速率的變化Fig.3 Case 1: line-of-sight rate profiles at different initial flight path angles via ISMDSG

圖4 情形1：ISMDSG方法不同初始彈道傾角時 視線角偏差的變化Fig.4 Case 1: line-of-sight angle error profiles at different initial flight path angles via ISMDSG

圖5 情形1：ISMDSG方法不同初始彈道傾角時 法向過載的變化Fig.5 Case 1: acceleration profiles at different initial flight path angles via ISMDSG

3.2 情形2：目標常值機動

本節針對常值機動目標，對比了本文提出的ISMDSG方法與TSG方法、NTSMG方法的末制導性能。

圖6 情形2：彈目運動軌跡比較Fig.6 Case 2: comparison of trajectories of projectile and target

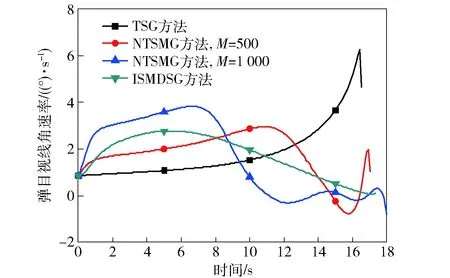
圖7 情形2：視線角速率的變化比較Fig.7 Case 2: comparison of line-of-sight rate profiles

3.3 情形3：目標周期性機動

本節針對周期性機動目標，對比了本文提出的ISMDSG方法與TSG方法、NTSMG方法的末制導性能。

圖8 情形2：視線角偏差的變化比較Fig.8 Case 2: comparison of line-of-sight angle error profiles

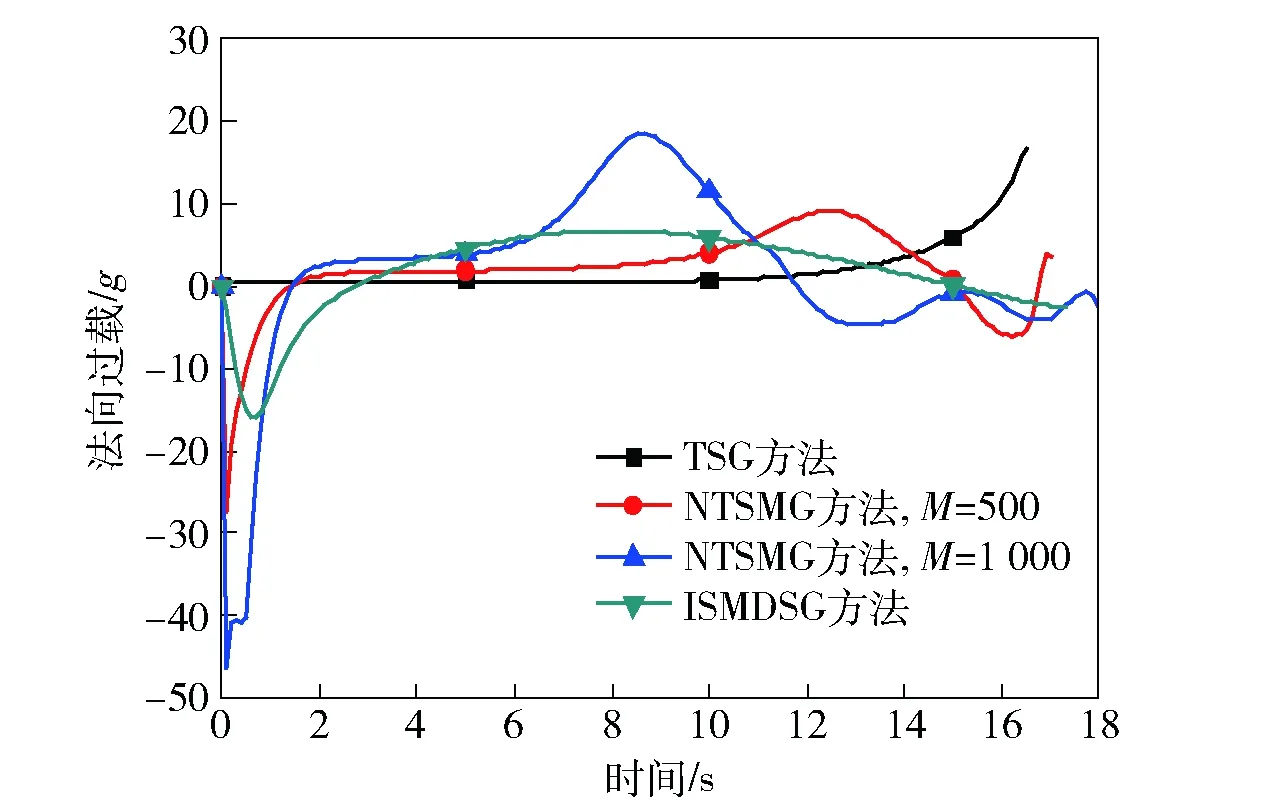
圖9 情形2：法向過載的變化比較Fig.9 Case 2: comparison of acceleration profiles

圖10 情形2：不確定項h及其估計值Fig.10 Case 2: uncertain term h and its estimated value 表1 情形2的脫靶量與飛行時間Tab.1 Miss distance and flight time for Case 2

參數TSG方法NTSMG方法M=500M=1000ISMDSG方法脫靶量/m542086093017飛行時間/s1654170218381731

圖11 情形3：彈目運動軌跡比較Fig.11 Case 3 comparison of trajectories of projectile and target

圖12 情形3：視線角速率的變化比較Fig.12 Case 3: comparison of line-of-sight rate profiles

圖13 情形3：視線角偏差的變化比較Fig.13 Case 3: comparison of line-of-sight angle error profiles

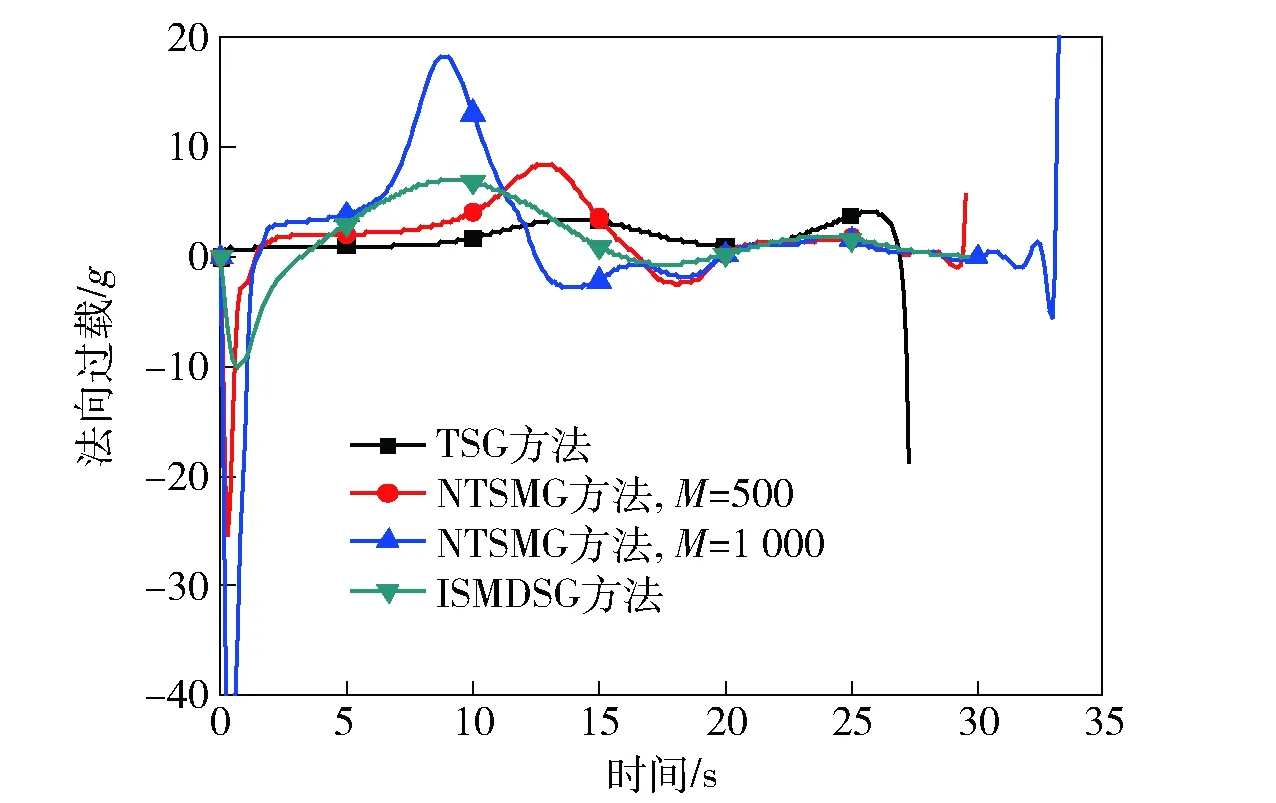
圖14 情形3：法向過載的變化比較Fig.14 Case 3: comparison of acceleration profiles

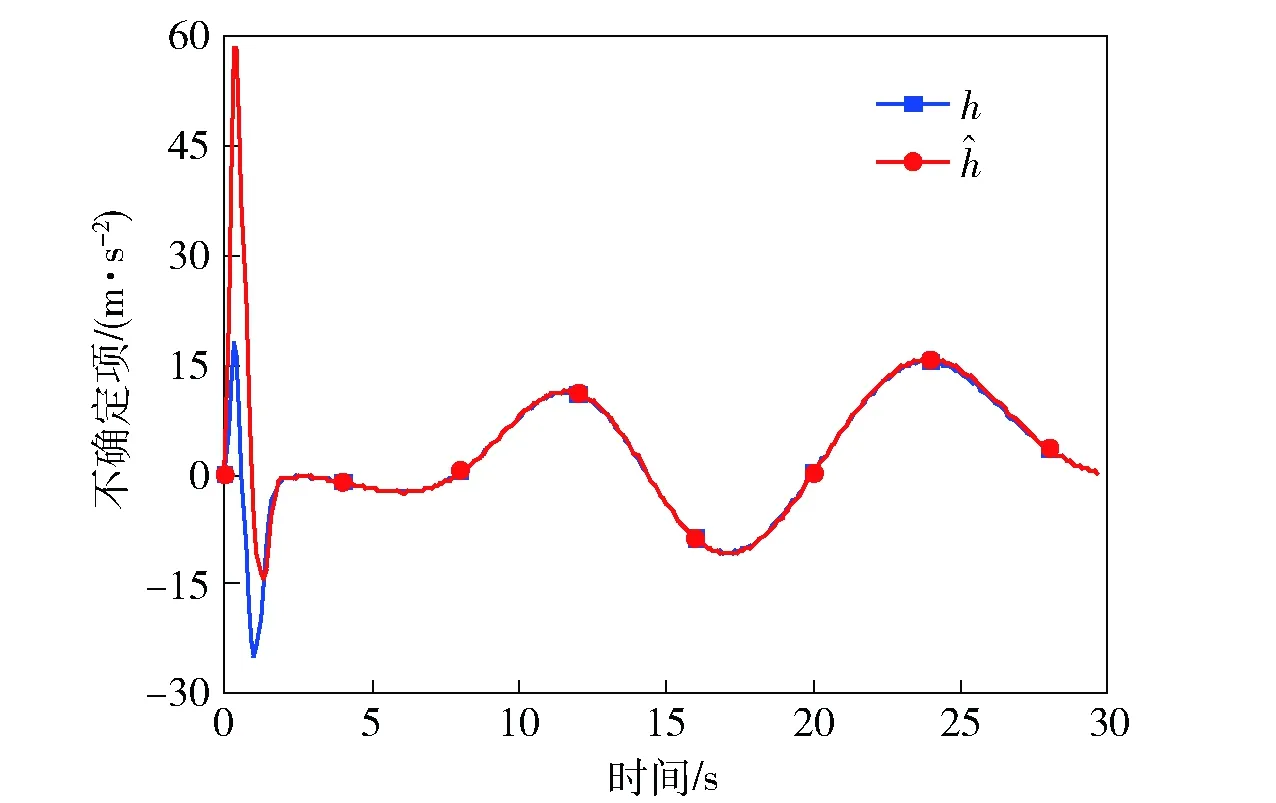
圖15 情形3：不確定項h及其估計值Fig.15 Case 2: uncertain term h and its estimated value 表2 情形3的脫靶量與飛行時間Tab.2 Miss distance and flight time for Case 3

參數TSG方法NTSMG方法M=500M=1000ISMDSG方法脫靶量/m856127133031飛行時間/s2732295833382966

4 結論

針對制導彈箭打擊機動目標時帶攻擊角約束的末制導問題，考慮自動駕駛儀動態特性對制導回路的影響，結合積分滑模與動態面控制方法，設計了一種新型魯棒末制導律。依據Lyapunov穩定性理論證明了閉環系統中視線角速率與視線角偏差均最終一致有界任意小，即實現了以一定的攻擊角命中目標。仿真結果表明：

1) 本文所提出的新型魯棒末制導律，在存在目標機動不確定及自動駕駛儀含擾動的條件下，可使制導彈箭以給定的攻擊角以高精度命中目標，且過載特性良好。

2) 當目標周期性機動時，若考慮攻擊角約束，會使得制導彈箭部分彈道曲率較大，可能需要其在大攻角條件下飛行，導致氣動非線性問題。另外，對于自主制導彈箭，較大的彈道曲率，可能導致導引頭無法跟蹤到目標。因此，在工程應用中要綜合考慮。

References)

[1] Kim M, Grider K V.Terminal guidance for impact attitude angle constrained flight trajectories[J]. IEEE Transactions on Aerospace and Electronic Systems, 1973, 9(6):852-859.

[2] Zarchan P. Tactical and strategic missile guidance[M]. Reston, VA, US: American Institute of Aeronautics and Astronautics, Inc, 2012: 569-576.

[3] Byung S K, Jang G L, Hyung S H. Biased PNG law for impact with angular constraint[J]. IEEE Transactions on Aerospace and Electronic Systems, 1998, 34(1): 277-288.

[4] 張春妍, 宋建梅, 侯博, 等. 帶落角和時間約束的網絡化導彈協同制導律[J]. 兵工學報, 2016, 37(3):431-438. ZHANG Chun-yan, SONG Jian-mei, HOU Bo, et al.Cooperative guidance law with impact angle and impact time constraints for networked missiles[J]. Acta Armamentarii, 2016, 37(3):431-438.(in Chinese)

[5] 張友安, 孫陽平, 方悅, 等. 帶落角和末端攻角約束的最優末制導律[J]. 海軍航空工程學院學報, 2013, 28(4):368-371. ZHANG You-an, SUN Yang-ping, FANG Yue, et al.Optimal guidance law with constraint on terminal impact angle and angle of attack[J]. Journal of Naval Aeronautical and Astronautical University, 2013, 28(4):368-371.(in Chinese)

[6] Cho H, Ryoo C K, Tsourdos A, et al.Optimal impact angle control guidance law based on linearization about collision triangle[J]. Journal of Guidance Control and Dynamics, 2014, 37(3):958-964.

[7] Rao S, Ghose D.Terminal impact angle constrained guidance laws using variable structure systems theory[J]. IEEE Transactions on Control Systems Technology, 2013, 21(6):2350-2359.

[8] Kumar S R, Rao S, Ghose D.Nonsingular terminal sliding mode guidance with impact angle constraints[J]. Journal of Guidance Control and Dynamics, 2014, 37(4):1114-1130.

[9] 刁兆師, 單家元. 考慮自動駕駛儀動態特性的含攻擊角約束的反演遞推制導律[J]. 宇航學報, 2014, 35(7):818-826. DIAO Zhao-shi, SHAN Jia-yuan. Back stepping guidance law with autopilot lag for attack angle constrained trajectories[J]. Journal of Astronautics, 2014, 35(7):818-826. (in Chinese)

[10] He S, Lin D, Wang J.Robust terminal angle constraint guidance law with autopilot lag for intercepting maneuvering targets[J]. Nonlinear Dynamics, 2015, 81(1/2):881-892.

[11] Swaroop D, Hedrick J K, Yip P P, et al.Dynamic surface control for a class of nonlinear systems[J]. IEEE Transactions on Automatic Control, 2000, 45(10):1893-1899.

[12] 熊少鋒, 王衛紅, 劉曉東, 等. 考慮導彈自動駕駛儀動態特性的帶攻擊角度約束制導律[J]. 控制與決策, 2015, 30(4):585-592. XIONG Shao-feng, WANG Wei-hong, LIU Xiao-dong, et al. Impact angle guidance law considering missile’s dynamics of autopilot[J]. Control and Decision, 2015, 30(4):585-592.(in Chinese)

[13] 張堯, 郭杰, 唐勝景, 等. 機動目標攔截含攻擊角約束的新型滑模制導律[J]. 兵工學報, 2015, 36(8):1443-1457. ZHANG Yao, GUO Jie, TANG Sheng-jing, et al. A novel sliding mode guidance law with impact angle constraint for maneuvering target interception[J]. Acta Armamentarii, 2015, 36(8):1443-1457.(in Chinese)

[14] Yamasaki T, Balakrishnan S N , Takano H, et al. Sliding mode based intercept guidance with uncertainty and disturbance compensation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(4):3331-3345.

[15] Shtessel Y, Edwards C, Fridman L, et al. Sliding mode control and observation[M]. NY, US: Birkh?user , 2013: 30-34.

[16] Levant A. High-order sliding modes, differentiation and output-feedback control[J]. International Journal of Control, 2003, 76(9):924-941.

Robust Terminal Guidance Law with Autopilot Lag andImpact Angle Constraints

YANG Jing， WANG Xu-gang， WANG Zhong-yuan， CHANG Si-jiang

(School of Energy and Power Engineering, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China)

A novel robust impact-angle-constrained guidance law with autopilot lag is proposed based on integral sliding mode and dynamic surface control for guided projectiles. The inner-loop autopilot is characterized by an uncertain second-order dynamics. The sliding mode variable is defined as a combination of the line-of-sight (LOS) rate and the LOS angle error with time-to-go in order to realize the guidance strategy and achieve a good acceleration performance during interception. The smooth nonlinear disturbance observer is adopted to obtain the model discrepancies from target maneuver and the speed variation of target and interceptor. The stability of LOS rate and the LOS angular deviation is proved in the sense of the uniform boundedness and ultimate boundedness. Simulated results show the effectiveness and superiority of the proposed robust terminal guidance law compared to the trajectory shaping guidance law and the nonsingular terminal guidance law.

ordnance science and technology; terminal guidance; impact angle constraint; integral sliding mode; dynamic surface control; disturbance estimator

2016-10-24

國家自然科學基金項目(11402117)

楊靖( 1988—)， 男， 博士研究生。 E-mail: jingyangnust@163.com

王旭剛( 1979—)， 男， 副研究員。 E-mail: wxgnets@163.com

TJ765.2+2

A

1000-1093(2017)05-0900-10

10.3969/j.issn.1000-1093.2017.05.009