帶有乘性噪聲的多傳感器強跟蹤融合算法

張虎龍

（中國飛行試驗研究院，陜西 西安 710089）

帶有乘性噪聲的多傳感器強跟蹤融合算法

張虎龍

（中國飛行試驗研究院，陜西 西安 710089）

為解決加性噪聲模型無法準確刻畫實際觀測模型的問題，采用帶有乘性噪聲系統模型進行建模。在實際系統中，由于多傳感器網絡的應用使得傳統乘性噪聲的濾波算法已無法滿足實際需求，該文分別提出帶有乘性噪聲的有反饋分布式和序貫式多傳感器強跟蹤濾波融合方法，以有效解決復雜環境下的非線性系統最優狀態估計問題。計算機仿真實驗表明，新算法具有很好的估計精度，在多傳感器目標跟蹤應用中有較好的應用前景。

數據融合；傳感器網絡；強跟蹤濾波；乘性噪聲

0 引言

R.E.Kalman于20世紀60年代提出的卡爾曼濾波器（KF）以最小均方差作為估計準則，采用遞推反饋形式估計最優狀態，大大降低了算法的時間和空間復雜度，被廣泛應用于目標跟蹤、導彈制導、智能交通等實踐工程應用中[1]。

經典的KF算法及其延伸出來的一系列非線性KF算法，如擴展卡爾曼濾波、無味卡爾曼濾波和強跟蹤濾波，都僅考慮了包含加性噪聲的觀測模型[2-3]。在實際工程中，由于環境的復雜性和觀測模型參數的不確定性導致以往的系統觀測模型無法準確表征系統觀測環境。為了更真實地反映系統觀測模型，帶有乘性噪聲系統模型應運而生，其本質上就是對經典線性卡爾曼濾波系統的推廣和優化，并以此發展出一系列的濾波算法[4-6]；不足的是，這些方法僅考慮了單傳感器情形。為提高目標狀態估計精度,基于傳感器網絡的融合系統及方法被大量使用[7-9]。傳感器網絡融合系統可以有效獲取可靠的觀測數據，但由于運動模型的不確定、環境的復雜性以及傳感器的多樣性使得當前帶乘性噪聲的濾波算法難以準確估計系統最優狀態。

因此，本文基于乘性噪聲系統模型，結合強跟蹤濾波技術，分別提出了有反饋分布式和序貫式多傳感器融合方法，解決復雜環境下多傳感器網絡的非線性融合問題。

1 系統模型

假設一類帶乘性噪聲的非線性系統，其狀態空間模型可描述[6]為

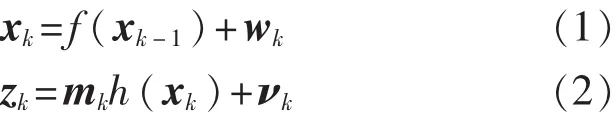
式中：mk為一維乘性噪聲；k（k=1，2，…，n）表示時間序列；狀態向量xk∈Rn，其中n表示狀態維數；觀測向量zk∈Rm，其中m表示觀測維數；f（·）、h（·）為非線性函數；過程噪聲wk-1∈Rn和觀測噪聲νk∈Rm分別為n維和m維的高斯白噪聲，其方程分別為Qk和Rk。

該模型是經典模型的優化版，在一定程度上可以對實際系統進行更精確地描述。當乘性噪聲恒定為1時，該模型則退化為經典模型。

2 強跟蹤濾波算法

2.1 線性化

對上述系統進行線性化處理，即圍繞濾波值x?k將非線性函數f（·）和h（·）進行泰勒級數展開，并略去二階以上項，即得線性化模型[2]如下：

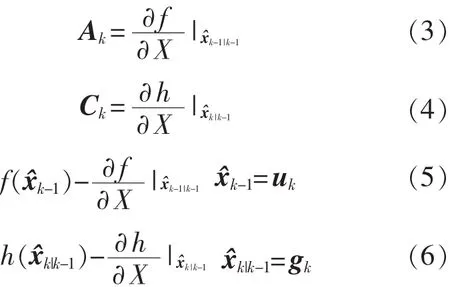
因此，經線性化處理后上述非線性系統的線性狀態空間模型[6]近似為

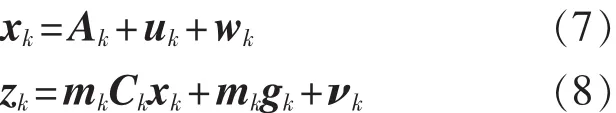
其中uk和gk分別表示狀態方程和觀測方程的隨機外作用項。

2.2 強跟蹤濾波

通常情況下，非線性系統采用擴展卡爾曼濾波（EKF）進行狀態估計，但在實際工程應用過程中，噪聲統計特性不準確或模型參數不確定等不確定因素的大量存在使得EKF的魯棒性能降低，無法有效估計系統狀態。為克服這些局限性，引入強跟蹤濾波（STF），其核心思想就是在EKF中引入漸消因子，通過在預測誤差協方差中引入漸消因子λk以弱化歷史數據對當前濾波的影響，以提高模型不確定的魯棒性和狀態突變的跟蹤能力[2]。

因此，帶有乘性噪聲的STF濾波過程為

狀態估計值：

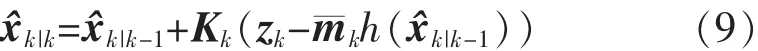
狀態預測值：

濾波增益值：

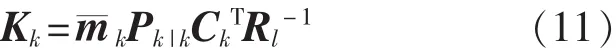
輸出殘差方差陣[6]：

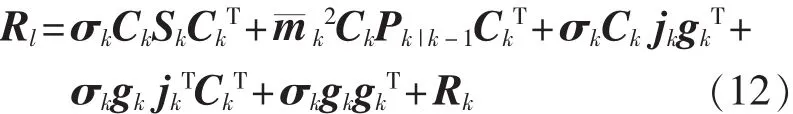
狀態相關矩陣：

狀態均值：

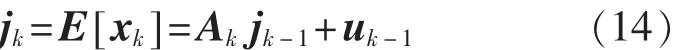
狀態預測協方差：

狀態估計協方差：

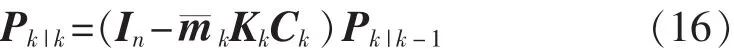
其中，漸消因子λk的計算過程[2]為

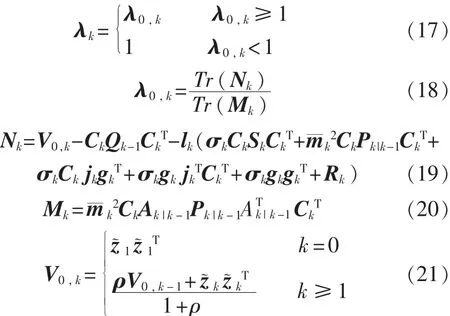
式中ρ為遺忘因子，0.95≤ρ≤0.995；lk≥1為弱化因子；且

3 多傳感器強跟蹤融合算法

假設N個傳感器以相同采用率對目標狀態進行觀察，觀測方程滿足[3]：

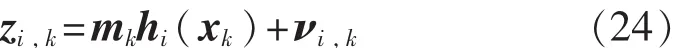
假設各子傳感器的乘性噪聲相同，則將N個觀測方程綜合成一個觀測方程即為

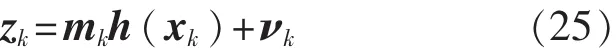
其中

3.1 分布式

利用強跟蹤融合算法估計狀態如下：

狀態估計值：

狀態估計協方差：

其中：

狀態預測值：

狀態預測協方差：

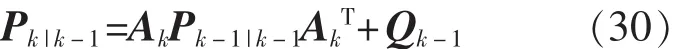
3.2 序貫式

基于x?k-1|k-1的一步預測估計值x?k|k-1和相應的預測誤差協方差陣Pk|k-1分別為

狀態預測值：

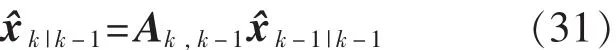
狀態預測協方差：

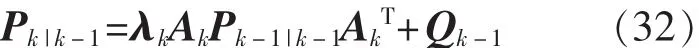
狀態估計值：

狀態估計協方差：

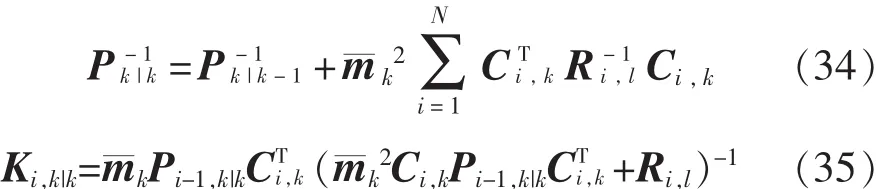
其中Ri，l根據式（12）～式（14）計算。

4 仿真分析

為對帶有乘性噪聲的非線性系統多傳感器數據融合算法有個清晰的認識，本文以笛卡爾坐標系下的目標跟蹤領域中的典型非線性跟蹤模型為研究對象[10]，以非線性強跟蹤卡爾曼濾波作為濾波估計方法，采用2個子傳感器并分別對上述有反饋式分布式多傳感器融合和序貫式多傳感器融合進行仿真驗證。其仿真結果如圖1和圖2所示。

給定各非線性跟蹤的狀態轉移矩陣和觀測方程如下式所示：

式中：xi，k——第i個狀態分量；

νi，k——第i個狀態的誤差分量；

Φ——系統在某時間段內的非線性跟蹤的狀態轉移矩陣和觀測矩陣。

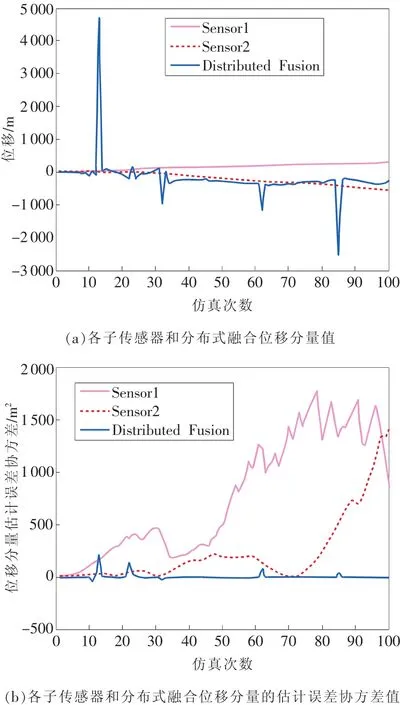
圖1有反饋分布式多傳感器融合算法

圖1 和圖2中粉實線和紅虛線分別表示2個子傳感器位移分量值及其相應的估計誤差協方差，藍線表示分布式和序貫式融合后的位移分量值及其相應的估計誤差協方差。由圖可知，針對帶有乘性噪聲系統模型而言，本文提出的有反饋分布式和序貫式多傳感器強跟蹤濾波數據融合濾波性能顯然優于各子傳感器的濾波性能。

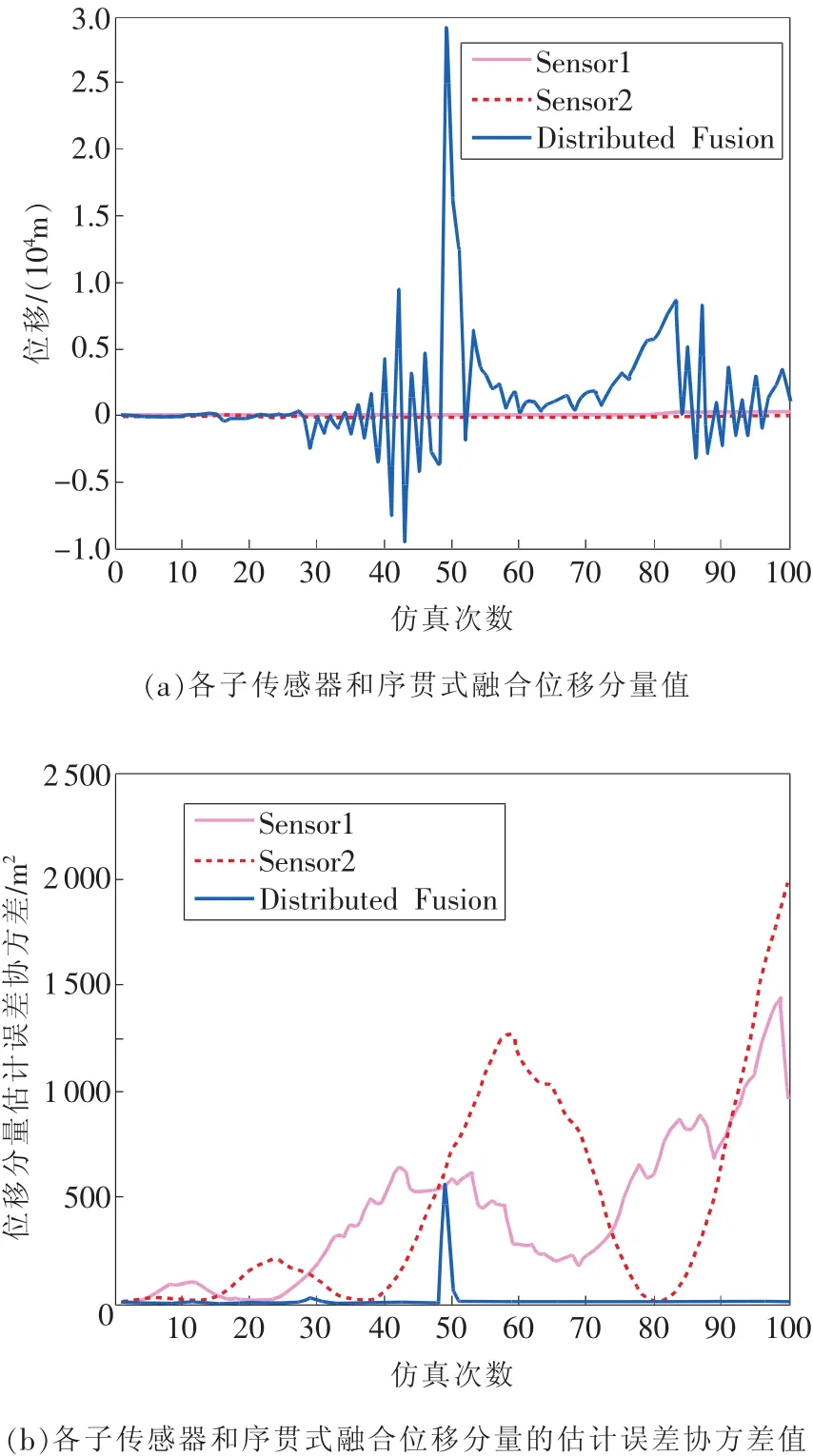
圖2 序貫式多傳感器融合算法

5 結束語

在實際系統中，由于隨著對系統精度要求的不斷提高，以及多傳感網絡采集數據的普及，以往僅包含加性噪聲的系統模型已無法滿足實際系統需求。本文提出有反饋分布式和序貫式多傳感器強跟蹤濾波數據融合方法，有效解決復雜環境下的非線性系統最優狀態估計問題，通過經典的非線性跟蹤模型對提出算法進行了仿真驗證和分析，驗證了算法的有效性和實用性。

[1]KALMAN R E.A new approach to linear filtering and prediction problems[J].Journal of Basic Engineering，1960，82（1）：35-45.

[2]付夢印，鄧志紅.Kalman濾波理論及其在導航系統中的應用[M].北京：科學出版社，2003：40-42.

[3]文成林.多尺度動態建模理論及其應用[M].北京：科學出版社，2007：76-79.

[4]褚東升，寧云磊，張玲.帶乘性噪聲系統狀態濾波的自適應算法[J].中國海洋大學學報（自然科學版），2011，41（12）：109-113.

[5]張玲，王蕊，褚東升.基于復雜多通道帶乘性噪聲模型的水聲通信字符估計算法[J].中國海洋大學學報（自然科學版），2015，45（1）：110-113.

[6]王昌盛，張玲，臧愛云，等.帶乘性噪聲附等式約束的非線性系統濾波算法[J].中國海洋大學學報（自然科學版），2016，46（8）：137-140.

[7]SONG Y，WANG B，SHI Z J，et al.Distributed algorithms for energy-efficient even self-deployment in mobile sensor networks[J].IEEE Transactions on Mobile Computing，2014，13（5）：1035-1047.

[8]XU Y F，CHOI J G，OH S H.Mobile sensor network navigation using Gaussian processes with truncated observations[J].IEEE Transactions on Robotics，2011，27（6）：1118-1131.

[9]YANG C B.Kalman filtering with nonlinear state constraints[J].IEEE Transactions on Aerospace and Electronic Systems，2009，45（1）：70-84.

[10]李超.基于非線性濾波的飛行器姿態確定算法研究[D].杭州：杭州電子科技大學，2011.

（編輯：李剛）

M ulti-sensors STF algorithms w ith multip licative noise

ZHANG Hulong
（Chinese Flight Test Establishment，Xi’an 710089，China）

In this paper，a multiplicative noise model is established to solve the problem that additive noise model cannot precisely describe the observed model.In actual systems，the filter algorithm of traditional multiplicative noise can no longer meet actual requirements owing to the application of multi-sensor network.Therefore，this paper puts forward respectively distributed and sequential multi-sensor strong tracking filter（STF）data fusion methods with multiplicative noise and feedback，in order to solve the optimal state estimation of nonlinear system in complex environment.Computer simulation experiments show that the new algorithm has good estimation accuracy，indicating a promising future application of multi-sensor target tracking.

data fusion；sensor network；strong tracking filter；multiplicative noise

A

1674-5124（2017）05-0101-04

10.11857/j.issn.1674-5124.2017.05.021

2016-11-18；

2016-12-24

航空科學基金（2015ZD30002）

張虎龍（1979-），男，湖南岳陽市人，高級工程師，研究方向為飛行試驗光電測試技術。