獨立卡爾曼濾波器全加速度計復雜振動角速度解算

汪偉，歹英杰，陳海龍，王平

（1.軍械工程學院，河北 石家莊 050003；2.防空兵學院，河南 鄭州 450052）

獨立卡爾曼濾波器全加速度計復雜振動角速度解算

汪偉1，歹英杰2，陳海龍1，王平1

（1.軍械工程學院，河北 石家莊 050003；2.防空兵學院，河南 鄭州 450052）

對于運動體的多自由度振動測試，準確的振動角速度是復雜振動參數解算的關鍵。針對目前解算角速度單一方法測試精度不理想的問題，分析由4個三軸加速度計組成傳感器陣列，測試角速度解算算法，設計一種獨立的卡爾曼濾波器用于角速度解算。通過仿真及實驗證明：該方法解算結果的誤差最大值和標準差相對于單一方法可提高1個數量級，其得到的角速度幅值準確性和曲線平滑度也優于其他單一解算方法。

加速度計；角速度；卡爾曼濾波;復雜振動

0 引言

振動測試對產品的可靠性、工況分析以及機械故障診斷等都有著重要的參考意義，測試車輛、艦船、飛機等運動體的振動狀態日益受到人們關注。針對運動體6個自由度運動同時進行測試，測試方法分為接觸式和非接觸式兩種。接觸式測量可采用3個陀螺儀和3個加速度計同時測量3個方向角速度和加速度，此方法缺點在于陀螺儀動態響應范圍小，價格昂貴且容易損壞。普通的單自由度多點測量，存在安裝繁瑣、布線復雜、多個傳感器之間相對位置測量和同步測試困難等問題[1]。非接觸式測量多采用多目CCD、光學經緯儀等測試技術，相比于接觸式測量，此類方法具有對被測物運動無干擾、測試精度高等優點；缺點在于測試設備復雜、操作困難、數據處理量大、動態測試范圍小，對于運動到視場以外的目標無法測量[2-3]。借鑒無陀螺捷聯慣性導航的相關技術，將傳感器陣列測試技術運用到振動環境中，可以有效地對較高頻率下多自由度線振動與角振動耦合效果進行絕對測量[4]，具有成本低、反應快、可靠性高等諸多優點，在工程上具有較廣闊的發展前景。本文介紹傳感器陣列測試技術，分析常用角速度解法優缺點，設計一種獨立的卡爾曼濾波器，運用到角速度解算中，在不需要外部觀測的情況下提高角速度解算精度。

1 全加速度計解算運動參數模型

1.1 空間任意點加速度

定義OnXnYnZn為慣性系，ObXbYbZb為載體系，如圖1所示。

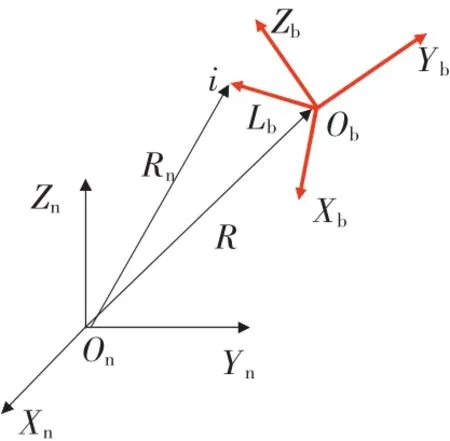
圖1 坐標系關系圖

根據運動學知識可以得到載體系上任意一點i位置的加速度值[5]為

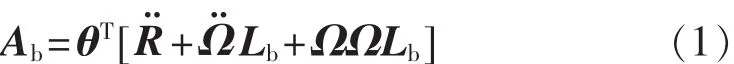
Lb——i點在載體坐標系中的位置矢量；

θ——i點傳感器在載體坐標系中敏感方向向量；

1.2 4個三軸加速度計配置方式

現有研究常用的有六加速度計、九加速度計、十二加速度計以及一些其他構型的傳感器陣列[5-6]。本文使用的是4個三軸加速度傳感器組成陣列的方案，不僅減少傳感器陣列中傳感器的使用個數，而且保證安裝在同一坐標軸的敏感方向的正交性，在狹小的空間中也便于安裝[7]。加速度計配置方式如圖2所示，其中A1～A4為傳感器安裝點位置，a1x～a4z方向為傳感器對應的敏感軸安裝方向。

4個三軸加速度計組成的十二加速度傳感器陣列的具體安裝位置和方向如表1所示。

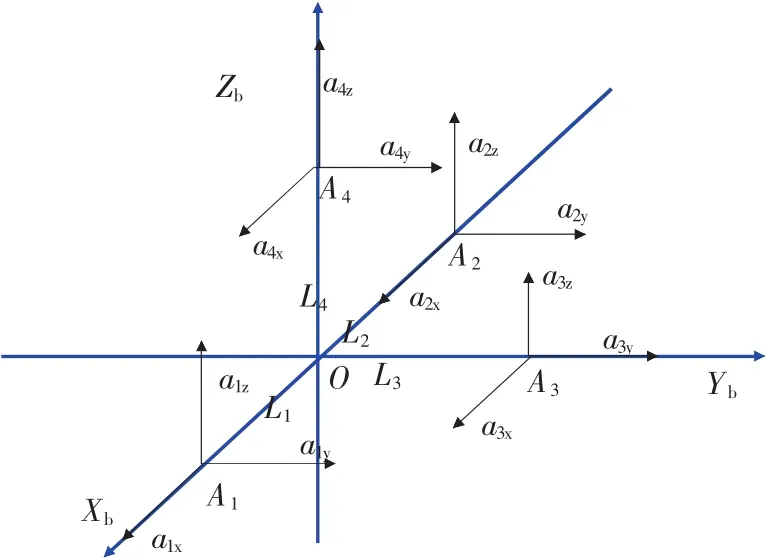
圖2 加速度計陣列構型

表1 十二加速度計安裝位置方向

1.3 振動參數的解算

剛體的運動可以用3個自由度的線運動和3個自由度的角運動來描述[8]。用a1x，a1y，a1z，…，a4z表示傳感器測試得到的加速度值，將L，θ代入（1）式可以解算得到剛體運動參數與測試加速度值關系式為

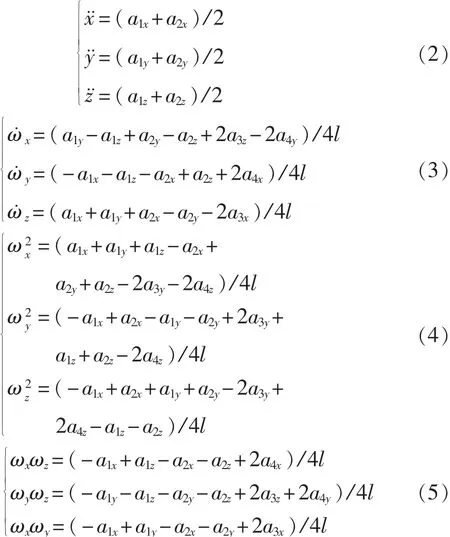
可以看出，根據加速度計值可以得到傳感器陣列繞載體坐標系的角加速度項和線加速度項。由角加速度積分等方法得到角速度后，將角速度代入姿態更新方程中，可以得到陣列任意時刻姿態，再由姿態信息和線加速度計算得到位置信息[8]。

2 角速度解算

2．1角速度解算算法

根據加速度計構型不同，由參數解算方程可以得到式（2）、式（3）、式（4）中角速度相關項的一個或多個表達式。根據角速度相關項解算式解算角速度主要有以下3種算法：

1）積分法。對角加速度項式（3）直接積分，可以得到繞載體坐標軸運動角速度表達式為

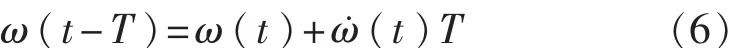
式中：t——采樣時刻；

T——采樣周期；

ω（t-T）——上一時刻積分得到的角速度。

2）開方法。對角速度平方項式（4）開方得到角速度的絕對值，再由通過式（6）積分得到的角速度確定角速度正負符號，即：

3）微分法。根據微分方程定義，可知

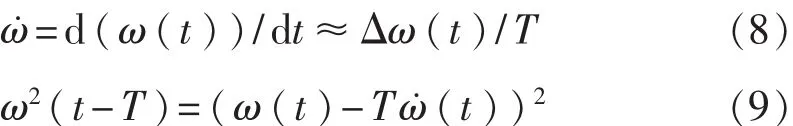
展開經簡單變換后得到角速度

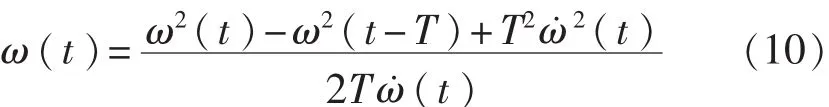
此方法也可以利用角速度交叉乘積項獲得。

2．2角速度解算誤差分析

由于加速度計實際安裝過程中，安裝位置和方向不可能和理論位置完全重合，存在安裝方向誤差和安裝位置誤差；其中，安裝位置誤差包括三軸加速度計芯片內部的敏感軸位置誤差和芯片整體安裝誤差[9]。在加速度計安裝、零位電壓和靈敏度等參數標定存在一定誤差時，利用加速度計測試得到的加速度值必然存在測量誤差。設傳感器理論測量值為A，測量誤差為ΔA，則加速度計實際測量值為

根據實際測量值解算角速度時，假設角加速度項解算誤差為Δω˙（t），則Δω˙（t）可表示為

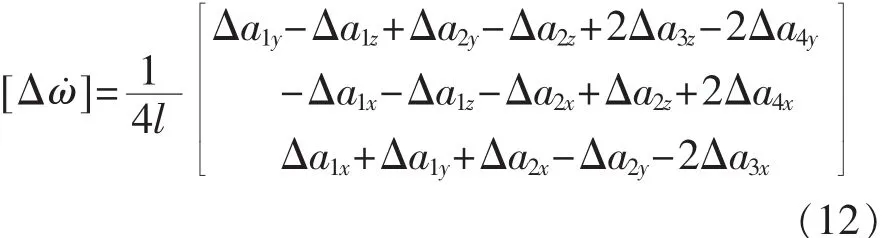
利用積分法解算角速度時，角速度表達式為

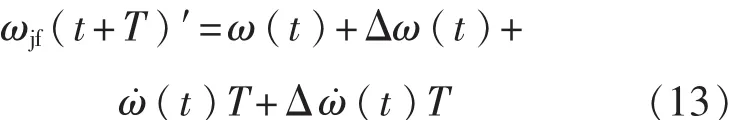
由式（13）可以看出，積分法角速度每一時刻的誤差都會帶到下一時刻角速度計算中，當角加速度誤差為非零均值時，式（13）得到的角速度會出現積分誤差，且隨測試時間增加誤差迅速增大[8]。

利用開方法解算角速度時，角速度表達式為

其中Δω2（t）表達式可由式（4）得到。利用式（14）得到的角速度不存在積分誤差問題，但隨著測試時間增加，由積分法得到的角速度符號可能越來越不準確，在角速度較小時可能出現符號誤判。

利用微分法解算角速度時，角速度表達式為

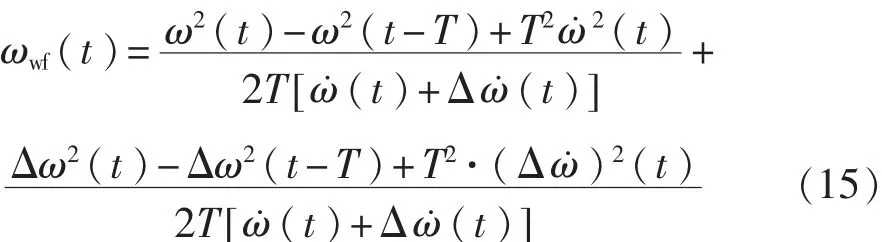
可以看出微分法求解角速度同樣不存在累積誤差，避免開方過程，不需要判斷符號。利用相鄰時刻差值解算，還可以消減一部分加速度計常值誤差，但在分母較小時會出現粗大誤差的情況[7]。

3 基于獨立卡爾曼濾波器的角速度解算

綜上可知，運用單一積分法、開方法或微分法求解振動角速度都有不可避免的缺陷：積分法得到的角速度誤差會累積發散，但誤差波動較小；開方法判斷符號受限于積分法角速度精度；微分法得到的角速度誤差不會累積發散，但相對于積分法，其誤差波動較大。雖然可以通過誤差補償方式，減少加速度計的測量誤差，但不可能完全消除測量誤差對角速度解算結果的影響。因此，提出利用積分法得到的角速度作為狀態變量，微分法得到的角速度作為觀測值，設計一種獨立的卡爾曼濾波器。

與從諸多信號中提取所需要信號的常規濾波有著本質的區別，卡爾曼濾波器通過一系列遞歸數學公式描述，從被提取信號相關量測量中通過算法估計出所需的信號[10]。因此，獨立卡爾曼濾波器適用于振動測試的隨機信號處理，而不需提前確定振動信號變化規律和其他角速度測量設備。

3．1系統狀態方程建立

根據積分法求解角速度的算法，角速度Xk可以表示為

其中Xk=[ωxkωykωzk]T為繞三軸轉動角速度，建立系統狀態方程為

式中Wk為未知系統噪聲，其協方差矩陣為Q；uk-1為狀態轉換控制項，表達式為

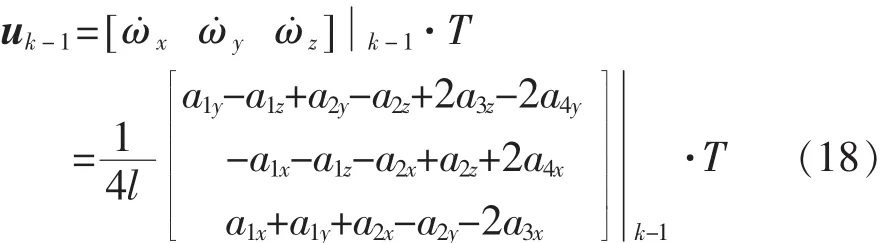
3．2觀測方程建立

根據開方法求解角速度法建立系統觀測方程：

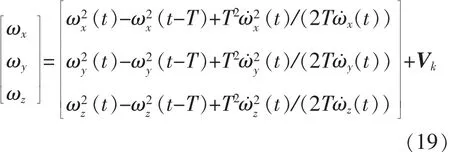
式中Vk為觀測噪聲，其協方差矩陣為R。

3．3狀態更新方程

在得到k-1時刻角速度最優估值后，其更新算法流程[11]如圖3所示。

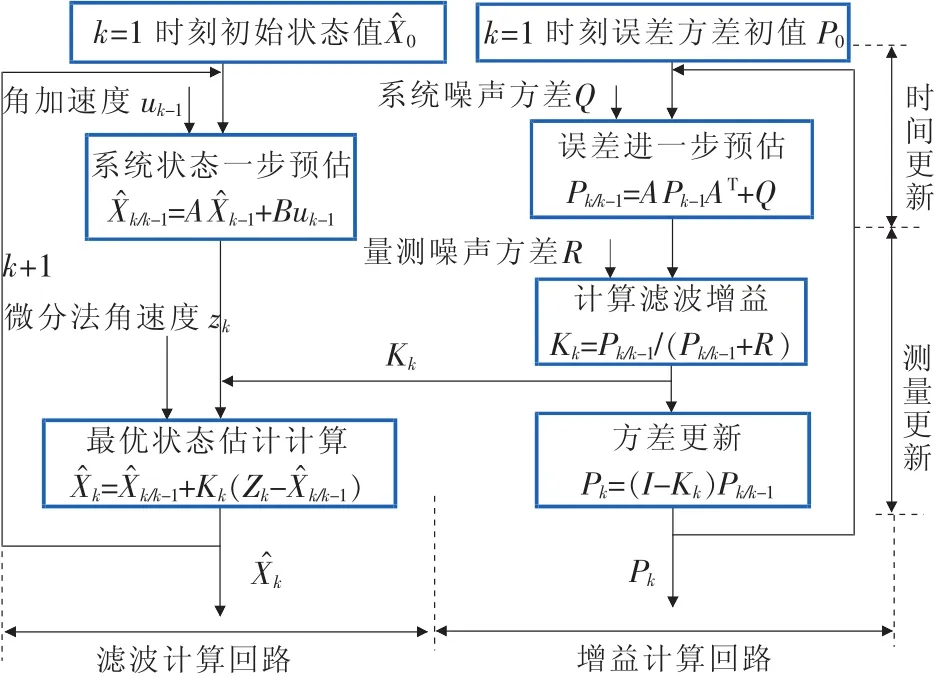
圖3 卡爾曼濾波算法流程

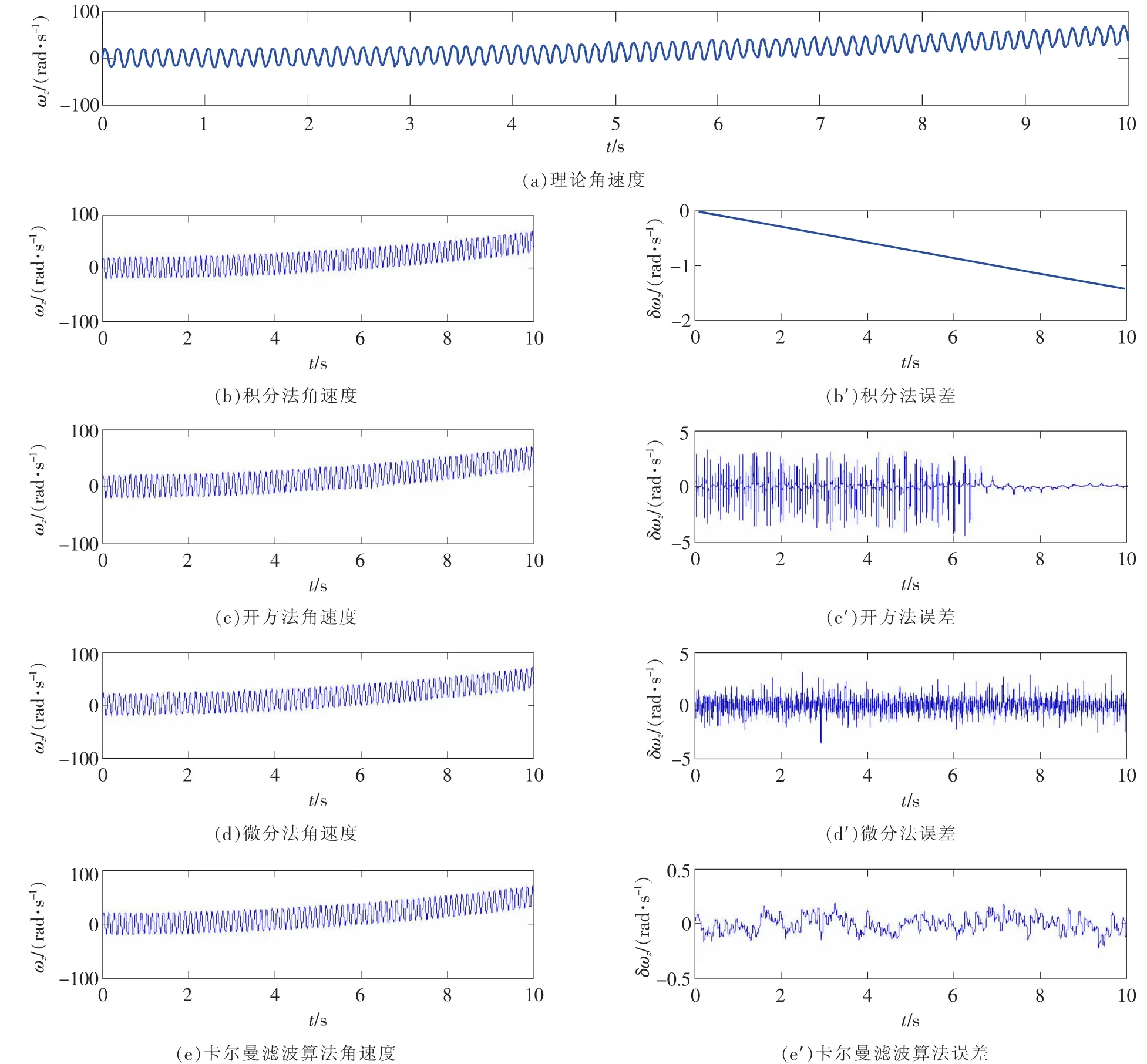
圖4 4種算法角速度及誤差曲線

1）狀態一步預估方程：

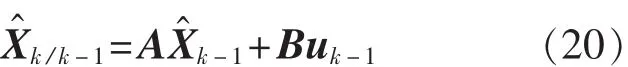
2）一步預測均方差：

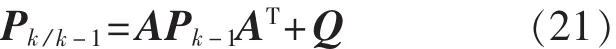
3）濾波增益為

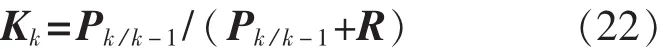
4）由觀測變量更新狀態變量：

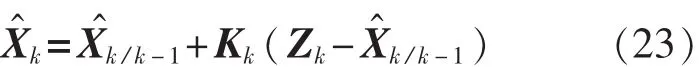
5）更新估計均方差：

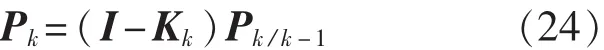
4 仿真驗證

采用如下模型進行仿真：仿真采樣頻率10kHz，采樣時間10s；不考慮加速度計安裝誤差，加速度傳感器常值誤差0.0001g，隨機噪聲的均方差為0.001g，安裝距離0.04m。角速度參數設置為

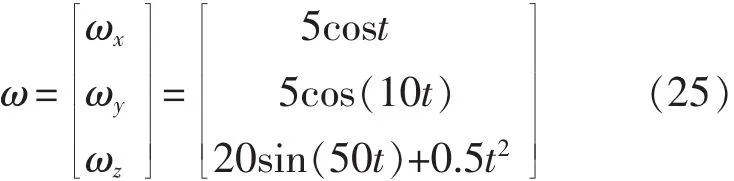
理論角速度，積分法、開方法、微分法和卡爾曼濾波算法4種算法計算角速度ωz及相應誤差如圖4所示。

由圖可知，積分法角速度誤差隨時間增長不斷增大。開方法角速度誤差收斂，角速度值在0附近時誤差較大，當角速度＞0且符號判斷正確時，誤差較小。微分法在角速度變化平緩時，容易造成粗大誤差，需要剔除，角速度變化較大時誤差較小。設計獨立的卡爾曼濾波器，根據積分法建立系統狀態方程，得到前一時刻的最優估計值后，利用加速度值作為狀態轉換的控制項進行一步預估，利用微分法得到的角速度誤差不發散的特點作為系統觀測值，對角速度值進行修正。表2為4種算法得到的角速度誤差統計。

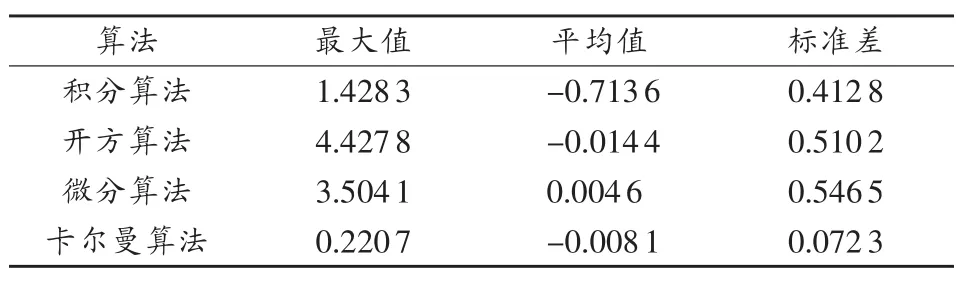
表2 角速度解算誤差統計rad/s

可以看出，卡爾曼濾波算法精度要高于其他單一解算精度，在誤差最大值和標準差方面準確度提高了1個數量級。因此可以假設此方法可以用于振動測試中被測物振動角速度解算。

5 實驗驗證

在角振動臺上進行角振動實驗，傳感器陣列坐標原點偏離旋轉中心一定距離，安裝位置示意圖如圖5所示。信號采集頻率1 kHz，時間20 s。振動臺以幅值30°、頻率2Hz的正弦模式進行角轉動。

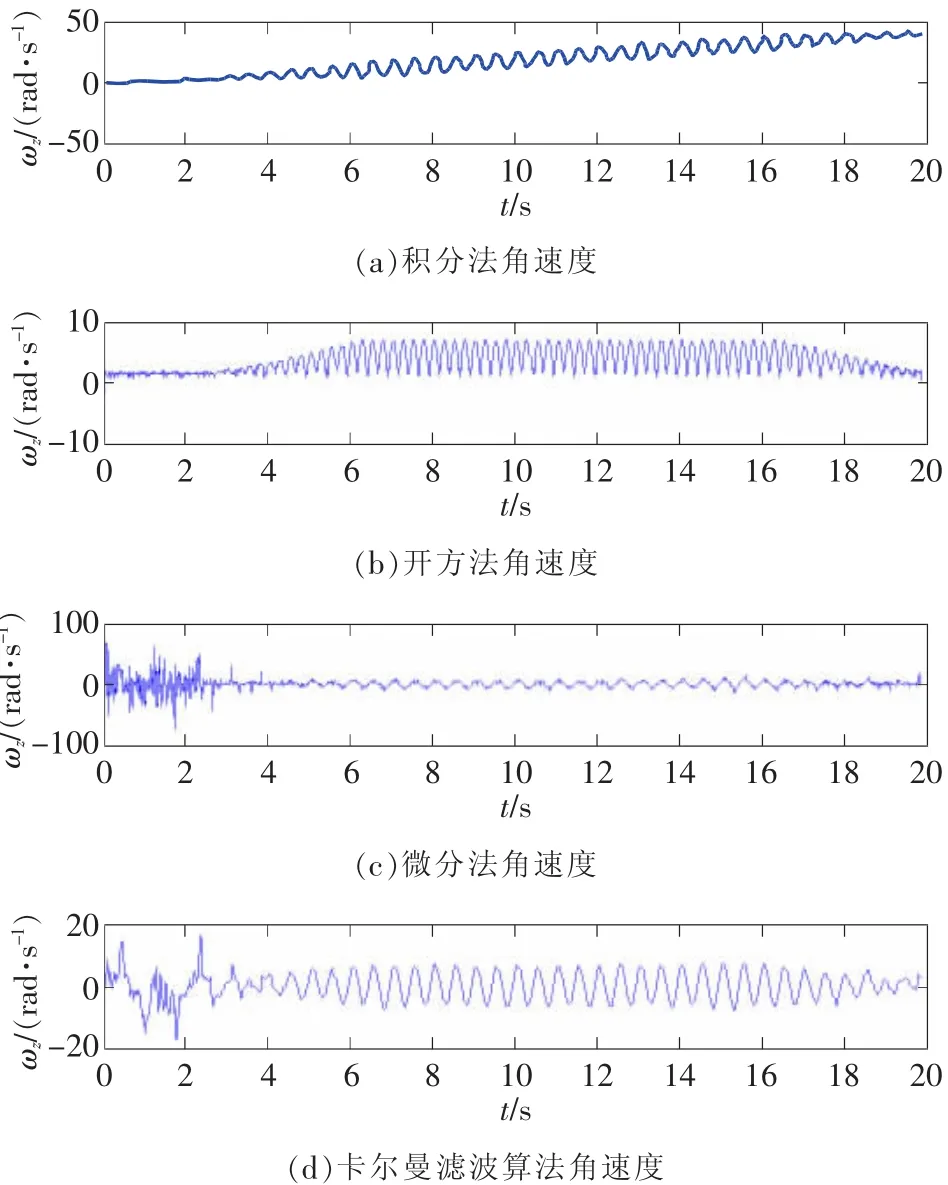
圖6 實驗角速度解算曲線

測試得到12組加速度計輸出后，分別用積分法、開方法、微分法和卡爾曼濾波算法解算載體轉動角速度，結果如圖6所示。

由圖可知，積分法解算得到的角速度，隨時間增長，按照一定趨勢不斷增大，偏離了實際結果。由于積分角速度已經偏離實際結果，造成開方法角速度的符號誤判，解算得到的角速度也偏離了實際結果。微分法解算得到的角速度在振動開始前，有很大誤差，在振動開始后，誤差變小；但在角速度變化較小時，其誤差相對來說也很大。卡爾曼濾波算法得到的角速度，在振動臺轉動之前，由于微分法角速度誤差較大，卡爾曼濾波算法得到的角速度誤差較大，振動臺轉動以后，測試效果要優于其他單一角速度解算算法。在利用開方法解算角速度時，對于出現的異常值可以通過預先判斷進行剔除，提高卡爾曼濾波算法角速度解算準確度。

6 結束語

借鑒無陀螺捷聯慣導知識，將加速度傳感器陣列技術用于運動體復雜振動測試。相比慣性制導，對計算實時性要求低，因此數據處理方法也更加靈活。本文介紹了傳感器陣列的排布構型和振動測試參數解算的方法，分析3種角速度解算常用方法的優缺點后，利用積分法和微分法分別作為系統狀態方程和觀測方程，設計一種不需要外部觀測的獨立卡爾曼濾波器。通過仿真證明，此方法應用于振動角速度解算中，其解算結果的誤差最大值和標準差相對于單一方法可提高1個數量級；通過實驗也證明該方法得到的角速度幅值準確性和曲線平滑度優于其他單一解算方法。

[1]張新，費業泰.多維加速度傳感器的設計及優化[J].中國測試，2007，33（3）：133-135.

[2]王宏亮，周浩強，高宏，等.基于雙等強度懸臂梁的光柵加速度振動傳感器[J].光電子·激光，2013，24（3）：635-637.

[3]羅波，李偉鵬，黃海.基于Stewart平臺的大柔性空間桁架結構振動控制[J].振動與沖擊，2012，31（23）：147-149.

[4]PARK S，WOO T C，PARKA J.A scheme for improving the performance of a gyroscope-free inertialmeasurement unit[J].Sensors and Actuators，2005（121）：410-420.

[5]史震，于秀萍.無陀螺捷聯式慣性導航系統[M].哈爾濱：哈爾濱工程大學出版社，2007：59-78.

[6]張會新，王世昌，楊運良，等.全加速度計慣性測量系統角速度解算方法的優化[J].中國慣性技術學報，2008，16（6）：672-675.

[7]焦建超，唐力偉，汪偉，等.六自由度振動測試新方案[J].新技術新工藝，2011（9）：67-69.

[8]尤晶晶，李成剛，吳洪濤.基于并聯機構的六維加速度傳感器的方案設計及建模研究[J].振動工程學報，2012，25（6）：658-665.

[9]LEE S C，CHENG Y L.Innovative estimation method with own-ship estimator for an accelerometer type inertial navigation system[J].International J of Systems Science，1999，30（12）：1259-1266.

[10]王璐，潘紫微，葉金杰.基于EKF訓練的RBF神經網絡及其故障診斷應用[J].振動、測試與診斷，2008，28（4）：358-361.

[11]顏翚，葛彤，楊柯，等.水下攻泥器隨鉆姿態慣性測量方法[J].上海交通大學學報，2012，46（3）：447-449.

（編輯：李剛）

App lication of Kalman filter to calculate angular velocity of com plicated vibration by full acceleration sensor

WANG Wei1，DAI Yingjie2，CHEN Hailong1，WANG Ping1
（1.Ordnance Engineering College，Shijiazhuang 050003，China；2.AIR Defense Forces Academy，Zhengzhou 450052，China）

For multi-freedom vibration test，the key of complicated vibration test is calculating the angular velocity.However，single method to calculate the angular velocity is not very ideal. Analyzing the angular velocity calculating algorithms by 4 tri-axial accelerometers，this paper puts forward Kalman filter to raise the accuracy of angular velocity.The simulation and experimental results show that this method is better and more accurate.

acceleration sensor；angular velocity；Kalman filter；complicated vibration

A

1674-5124（2015）05-0105-05

10.11857/j.issn.1674-5124.2017.05.022

2016-07-15；

2016-08-13

汪偉（1963-），男，教授，博士生導師，主要從事測試技術理論研究工作。