一類含絕對值恒成立問題的解法研究
筅江蘇省揚中市第二高級中學陳桂明
一類含絕對值恒成立問題的解法研究
筅江蘇省揚中市第二高級中學陳桂明
我們知道,高三數學教學主要是解題教學,因此解題研究是高中老師必做的功課,下面筆者以一道習題為例,談談高中數學解題教學的一些思考.
一、題目呈現
⑴求f(x)在區間[0,1]上的極值;
此題是高三復習時的一道題,題面熟悉,但是學生的解答并不理想.下面針對第(2)問我們來分析學生遇到的困惑.
二、學生的困惑
錯誤2:從命題的否定入手:
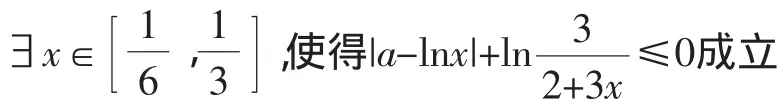
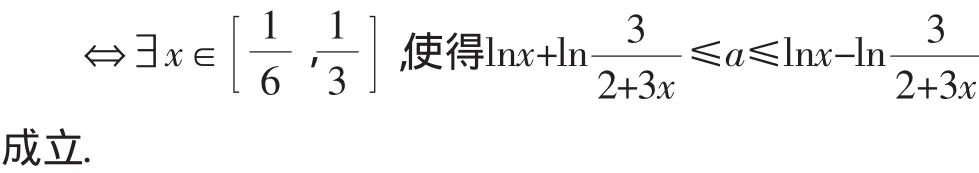
我們知道,解題錯誤的原因總有其內在的合理性,解題分析首先要對合理成分給予充分的理解;要通過反例或啟發等途徑暴露矛盾,引發當事者的自我反省;要正面指出錯誤的地方,具體分析錯誤的性質;這兩種解法思路沒有錯,那問題到底又出在哪兒?此類問題一般的求解思路又是什么?
錯誤1利用了結論|f(x)|>g(x)圳f(x)>g(x)或f(x)< -g(x)進行轉化,該結論本身并沒有錯,但在恒成立問題上遇到了麻煩,①到②及③到⑦的轉化也都沒有問題,問題就出在②到③的轉化,也即學生將“坌x∈D,a>f(x)或a 有的同學根據含絕對值的恒成立問題的解決辦法:設函數f(x),g(x)的定義域為A,f(x)+g(x)是連續函數,且滿足g(x)≥0.則坌x∈A,|f(x)|>g(x)成立的充要條件為坌x∈A,f(x)≥g(x)或坌x∈A,f(x)<-g(x). 其中問題是將“堝x∈D,f(x)≤a≤g(x)成立”圳“”時,未注意到g(x)-f(x)≥0這一前提,從而忽視了x范圍的改變.由此題中,即x≥ 解法1:按a分類討論: 解法3:從命題的否定入手: 1.重視“研”題目,促進深度探究 在平時的教學中,要帶著一種研究的態度去做題,深入探究試題解法的多樣性,培養學生的發散思維,使得學生能在以后的解題中獲得較為合理和簡潔的運算途徑和思維方法.葉瀾教授曾說:“課堂是向未知方向挺進的旅程,隨時都有可能發現意外的通道和美麗的因素,而不是一切都必須遵循固定路線而沒有激情的行程.”課堂教學過程是復雜的、豐富多變的,難免會遇到超出預設方案之外的新問題、新想法,教師應善待學生提出的“意外”問題,尊重學生的“話語權”,為學生營造一個敢于發表自己見解、勇于說出自己想法的平臺,適時調整教學設計方案,為學生的“動態生成”騰出一片廣闊的空間,并因勢利導,借題“發揮”,提升復習效益.課堂上只有真正放手讓學生做,才會為學生創造探究的機會,才能真正發揮學生學習的主觀能動性,才能引發學生的認知沖突,激發學生的思維火花,才能更好地做好“研”題目. 2.追求“慢”教學,激活學生思維 為什么會經常出現“聽起來頭頭是道,做起來莫名其妙”的現象,這與平時我們不敢放手課堂,課上老師講得多,課下學生練得少有很大關系.對數學知識的學習應該是一個循序漸進、不斷感悟和深化的過程,因此,數學要追求“慢”教學,要以學生為本,在教學過程中不斷設置有利于激發學習潛能,鍛煉學生思維的問題和情境,實現課堂效益最大化.另外,數學教學內容的呈現還要利于學生自主探究,在交流互動中體驗知識的產生和發展,在思維碰撞中經歷數學的發現和創造,只有“慢”教學,才能讓知識的剖析更為細膩,讓習題的輻射更為廣泛,讓學生的體驗更為深刻,才能更多地為學生提供“說”和“做”的時間和空間.而沒有數學思考,就沒有真正的數學學習,只有學生通過自己的思考建立起自己的數學理解力時,才可以說對知識達到了較高程度的掌握.故而,課堂上教師應提倡“慢”教學,尊重學生的“第一思考權”,尊重學生的認知規律,以“學為中心”展開教學過程,多給學生“想一想”的時間,多給學生數學思維鍛煉和表達的機會.因此,課堂教學應當使學生身心處于和諧寬松的教學生態中,從學生的眼神中讀出內心的感受,從學生的表情上看出思維的起伏,從學生的言行中評估教學成效,從師生的互動交鋒中演繹教學的精彩,這一切都需要教師在教學活動中等待、耐心、從容、寬容、期待、優雅,數學課堂“慢”教學的生態性注重學生心理感受、成功體驗、快樂成長,“慢”在教學中是一種心境,更是一種藝術,也是孕育教學動態生成的精彩歷程.三、拓展探究
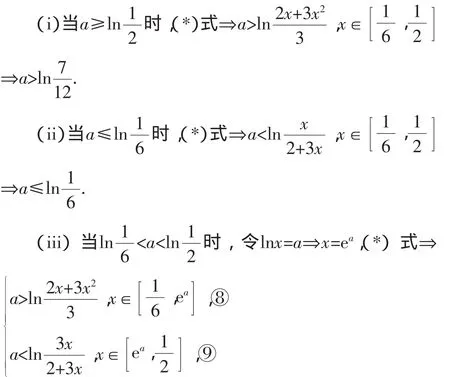
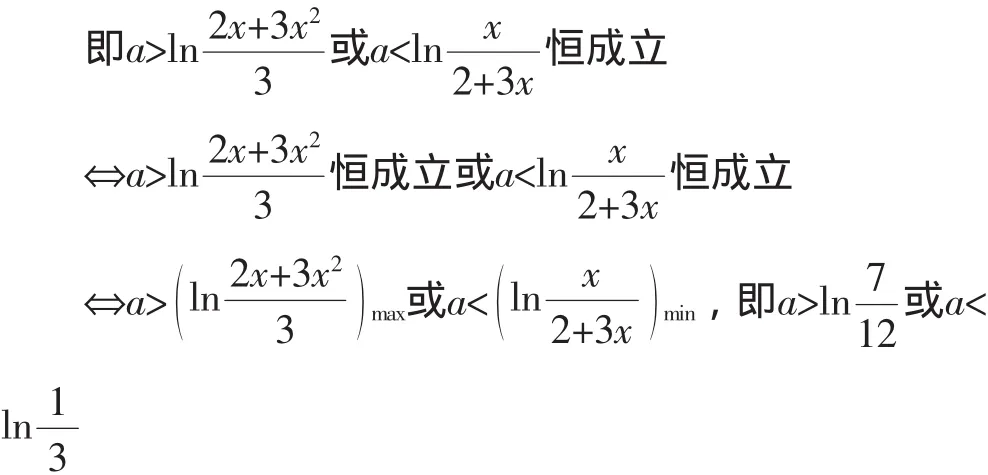
四、幾點思考

