定平面形狀乘波體及設計變量影響分析
劉傳振,白 鵬,陳冰雁,周偉江
(中國航天空氣動力技術研究院,北京100074)
定平面形狀乘波體及設計變量影響分析
劉傳振,白 鵬,陳冰雁,周偉江
(中國航天空氣動力技術研究院,北京100074)
拓展密切錐方法的設計靈活性,提出了一種定平面形狀乘波體概念。推導了設計參數與平面形狀之間的泛化幾何關系,使用非均勻有理B樣條輔助設計,建立了頭部區域可控、后掠區域可控的雙后掠乘波體設計方法,并給出了此類乘波體外形參數與設計參數之間的幾何關系。結合考慮黏性的乘波體性能快速預估方法評估乘波體性能,并通過CFD技術驗證了設計和性能評估方法的有效性。提取設計變量,分析典型變量對乘波體性能的影響。結果表明,雙后掠乘波體保持了高超聲速階段的高升阻比特性,同時具有對平面形狀良好的可控性,為構建新型乘波體外形提供了思路。
乘波體;定平面;雙后掠;設計變量;氣動性能
0 引 言
近年來,具有高升阻比特性的乘波體成為了國際研究的重點和熱點。Nonweiler[1]在1959年首先提出了乘波體設計理論,并通過楔形流場生成了‘Λ’型乘波體,Jones等[2]提出了使用軸對稱錐形流動的錐導乘波體概念,增大了飛行器的容積,推動了乘波體飛行器的實用化。很多學者為擴大設計空間,發展使用了其他基準流場,包括帶攻角的錐、橢圓錐流動[3]、一般三維流動[4-5]等。1990年,Sobieczky等[6]提出密切錐乘波體設計方法,通過給定激波形狀擬合流場,可以生成具有更多特性的乘波體外形,靈活性很高。
但乘波體仍然有一些缺陷限制了它的工程應用,主要包括容積率不高,低速狀態氣動性能不好,縱向穩定性難以保證等。目前有一些解決方法,例如修改上表面外形擴充容積,串聯不同展長的外形進行改善低速狀態性能[7],改變基準流場部分提高縱向穩定性[8]等。這些方法具有較好的工程應用價值,但或是在外形生成之后進行修形,或難以提取設計參數進行控制,可控性不足。乘波體的曲面通過追蹤流線得到,可修改性較低,而平面形狀的設計自由度較高,因此控制平面形狀生成乘波體外形是改善乘波體性能缺陷的新的思路。
對定平面形狀乘波體有意義的探索是定后掠角乘波體,但在早期只是作為傳統方法的附屬。Starley等[9]提出了定常楔形角乘波體,因為采用了二維楔形流場,升阻比不高,體積利用率較低;Jones等[2]在介紹錐導乘波體時,提到過一種設計曲線過圓錐頂點的乘波體,但設計空間受限,方法不夠靈活;最近幾年,洛克希德馬丁公司的Rodi[10]從密切錐乘波體設計方法出發,介紹了定后掠角密切錐和密切流場乘波體的概念;段焰輝等[11]給出了定后掠角乘波體具體實現,并提取設計變量進行了分析研究。
本文從定后掠角乘波體設計方法出發,推導了設計曲線與乘波體外形之間的全域性關系,對設計曲線進行拓展提出了定平面形狀乘波體概念,重點研究了其中的雙后掠外形。使用非均勻有理B樣條(Non-uniform rational B-spline, NURBS)輔助設計,保證了雙后掠乘波體曲面的連續光滑。使用CFD技術驗證設計方法的有效性,并考察了設計變量對于雙后掠乘波體性能的影響。
1 設計方法
1.1 兩個重要的幾何關系
密切錐乘波體設計方法可以由給定的激波形狀擬合流場生成乘波體,設計方法中需要給出的設計曲線包括激波出口型線,也叫做進氣捕獲曲線(Inlet capture curve, ICC),和流線追蹤的初始線-捕獲流管(Flow capture tube, FCT)。在密切錐乘波體設計中,ICC曲線和FCT曲線的形狀直接決定了乘波體的外形。本節討論設計曲線與生成外形之間兩個有用的幾何關系,分別可以確定乘波體外形的平面形狀和厚度分布。
圖1給出了密切錐乘波體設計方法的局部示意圖,作ICC曲線在G點的切線,過此點的垂面GH即為密切平面,密切平面內使用錐形流擬合,錐形流動有幾個重要假設:1)激波平直,激波角為定值β;2)錐形流中所有的流線都是自相似的[12],可設定流線傾斜角等同于錐角γc。錐形流動一般采用數值方法求解Taylor-Macoll方程得到,尺度由ICC的當地曲率半徑決定,如果ICC為直線,曲率半徑無窮大,可使用二維楔形流動代替。H點為密切平面與FCT曲線的交點。ICC在G點斜率傾角為δ,FCT的斜率傾角為δ1,生成乘波體部分的長度為l,寬度為s。有關系式:

(1)
求解得到:
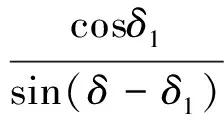
(2)
λ是當地前緣后掠角,在密切錐乘波體設計方法中,此條件全域性的,即使ICC和FCT曲線不為直線此公式也成立。
第二個關系是下表面偏轉角關系,如圖2所示,δ2為流線追蹤法得到的乘波體下表面后緣(LS)在I點的斜率傾角。
有如下的關系:
(3)
得到
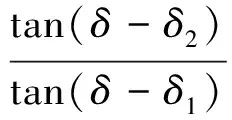
(4)
1.2 定平面形狀乘波體設計
流場和激波的影響對乘波體性能更具決定性,在應用幾何關系式時,簡單起見,可以將FCT設定為水平直線,式(2)簡化為文獻[10]中提到的關系:
sinδ=tanλtanβ
(5)
根據式(5),當ICC存在斜率為0的直線時,對應乘波體外形部分后掠角為0,ICC存在為斜率不為0的直線時,對應外形為定后掠前緣,當ICC為一般曲線時,對應的外形的輪廓線為曲線,因此這個關系式允許我們通過給定ICC曲線的斜率和曲率定制乘波體的外形。圖3給出了綜合以上結論得到的平頭前緣乘波體,通過ICC的斜率曲率可將乘波體分為平頭部分,彎曲部分和后掠部分。
平頭前緣乘波體有一定的研究意義,但更具有實用價值的是彎頭或尖頭外形。
如圖4所示,去掉斜率為0的直線部分,ICC靠近對稱軸部分設定圓弧段,直線段與圓弧不相切。一般取直線段傾角小于圓弧圓心角,否則導致乘波體曲面重疊。通過密切平面與FCT曲線的交點可以將FCT分為彎頭區域、第一后掠區域和第二后掠區域,同時設定第一后掠區域的曲率由圓弧到直線逐漸過渡。所生成乘波體的平面形狀類似雙后掠布局,如圖4所示。
圖4所示的設計參數與乘波體平面形狀控制參數之間存在對應的幾何關系,設O點為坐標原點,圓弧半徑為R,FCT偏移距離為r,圓弧圓心角為θ1,直線段傾角為θ2。計算乘波體的長度l,寬度s和彎頭區域寬度sb:

(6)
當r=0時,所生成的外形為尖頭乘波體,當r=Rcosθ1時,此設計方法方法退化為FCT為水平直線的錐導乘波體。r不夠直觀,后文使用彎頭度
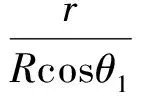
將其歸一化。
第一和第二后掠區域的寬度s1,s2為:
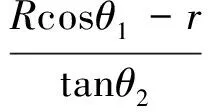
第一后掠區域前緣線不是嚴格意義的直線,可近似取T1T2兩點的斜率角為第一后掠角λ1:
(7)
第二后掠角λ2可根據式(5)計算:
(8)
第二后掠區域的厚度分布角ε(與圖2中的δ2對應)由式(4)求解:
(9)
根據式(6)~(9)即可通過彎頭區域寬度、后掠角大小和厚度分布角求取r、β、θ1、θ2進行乘波體設計。
1.3 使用NURBS輔助設計
圖4方法中,后掠區域的大小是固定的,難以控制;直線段斜率傾角與圓弧圓心角差距過大時,過渡點處斜率變化劇烈,可能影響下表面在對應位置的光滑分布。
為解決這些問題,本文引入非均勻有理B樣條(Non-uniform rational B-spline, NURBS)表達ICC曲線輔助設計。分析圖4中ICC曲線的構成,主要包括圓弧和直線部分。NURBS方法的最大優點之一就是能夠精確的表示包括圓在內的圓錐截線[13],這一特性給了我們很大的便利進行密切錐的設計。p次NURBS曲線的定義為:
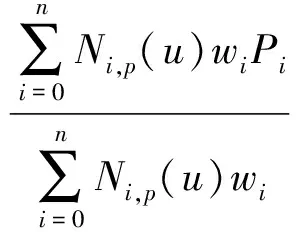
(10)
其中Pi是控制點,wi是權因子,Ni,p(u)是定義在非周期非均勻節點矢量上的p次B樣條基函數。
NURBS方法可以通過給定半徑R和圓心角γ得到特定的控制點生成圓弧,直線則通過共線的p+1個點生成。
圖5給出了使用二次NURBS表達包括圓和直線在內的曲線輔助乘波體設計的示意圖,為了控制第一后掠區域的范圍,本文增加過渡段,同時使用重節點技術控制曲線保證圓和直線互不干擾。具體實施如下:點AEBFCD為NURBS生成ICC曲線的控制點,其中AEB確定圓弧部分,圓心角為θ1,FCD共線,產生斜率傾角為θ2的直線,BFC點控制圓弧與直線的過渡段。F點的位置很重要,控制了第一后掠區域的大小,也影響了乘波體的總寬度,F點位于圓弧在B點的切線向上,給定參數0≤ω≤1在切線段上控制F點的位置,當ω=0時,F與B重合,方法退化為圖4所示的雙后掠乘波體設計,當ω=1.0時,F點到達FCT曲線,方法退化為單后掠乘波體設計。
增加了控制參數ω之后,乘波體的平面控制參數可以求得:

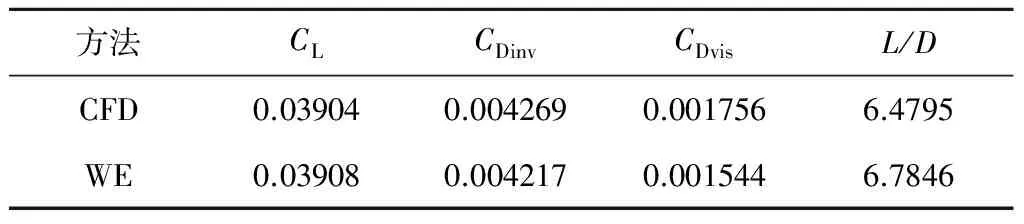
NURBS曲線的節點矢量為[0,0,0,a1,a1,a2,1,1,1],0.0 使用NURBS表達ICC曲線,保證了第一后掠段斜率和曲率的光滑過渡,使乘波體平面形狀和表面曲面的過渡更加光順,同時增加了參數ω控制后掠段的區域大小。設計方法非常靈活(見圖6),可以方便改變頭部區域和后掠區域的形狀,具有給定平面形狀設計乘波體外形的能力。編制FORTRAN程序,生成一個外形的時間不超過1秒,效率很高。 2.1 設計變量選擇 以雙后掠乘波體為例,定平面形狀乘波體的設計參數包括圓弧半徑R,彎頭度ζ,激波角β,ICC曲線的偏轉角θ1和θ2,第一后掠區域控制量ω,根據第1.2和第1.3節的分析,通過這些控制參數即可以確定乘波體的長度l,寬度s,彎頭區域sb,第一、第二后掠區域s1,s2,第一第二后掠角大小λ1,λ2,下表面厚度分布角ε等形狀控制參數。相對應的,也可以通過外形控制參數得到設計參數進行乘波體設計,因此設計變量可以選取設計參數或外形控制參數。簡單直觀起見,本文選定的設計變量為R,ζ,β,λ1,λ2,ω。 2.2 性能評估方法及驗證 使用密切錐進行乘波體設計時,乘波體外形一般從無黏流場出發通過流線追蹤得到,所生成的外形中存儲有無黏流場信息,因此可以通過流線積分法評估無黏氣動力。 高超聲速條件下,黏性力在阻力中占有很大的比重,因此在考慮乘波體設計中需要把黏性效應考慮進去。本文使用基于流線的黏性力計算方法[14],將流線與參考溫度法結合[15],提高了計算方法的精度。 沿流線計算流線長度并由此計算邊界層外緣的當地雷諾數,定義為: (11) x為當地流線長度,ρδ,Uδ和μδ為當地的密度、速度和黏性系數。求得當地雷諾數后,根據下式將其修正為不可壓的當地雷諾數: Rexin=FReRexδ 不可壓平板的當地黏性力系數計算公式為: 計算得到不可壓平板當地黏性力系數后,使用Cfcom=Cfin/Fc修正為可壓縮黏性力系數。在這種方法中,修正因子Fc和FRe是與馬赫數和溫度相關的函數,工程應用中可使用參考溫度法[16]計算,參考溫度法的思路是將附面層中某處的狀態近似的看做物面狀態。修正因子與參考量之間的關系為: (12) 式中:μ*=f(T*)為參考黏性系數,可由Sutherland公式求得;ρ*=g(P*,T*)為參考密度,可根據氣體狀態方程求得。因為附面層中壓強的法向梯度為零,所以P*=Pδ。參考溫度T*由下式確定: (13) TW是壁面溫度,T∞,M∞為自由來流的溫度和馬赫數。 流線積分法和基于流線的參考溫度法作為乘波體的快速預估方法(Waverider estimation, WE)效率很高,但精度不能保證。本文使用計算流體力學(Computational fluid dynamics, CFD)技術對其進行驗證計算,計算網格為非結構網格,湍流模型使用S-A模型。設計狀態為馬赫數Ma=5,高度H=30km,選擇外形的設計變量為λ1=75°,λ2=50°,ζ=0.001,ω=0.2,β=14°。 氣動力結果如表1所示,CL,CDinv,CDvis分別代表升力系數、無黏阻力和有黏阻力系數,升阻比L/D的誤差在4.7%左右,可以看到計算結果是比較相近的,驗證了本文乘波體性能快速計算方法的有效性。圖7給出了乘波體下表面的等壓線,可以看到激波整體附著在前緣,高壓區氣流整體被束縛在激波內部,具有明顯的乘波效應,不考慮底阻的升阻比為6.5左右,保持了設計狀態的高升阻比特性。圖8給出了設計激波曲線與CFD模擬結果的對比,激波形狀除在轉折處存在誤差外在大部分擬合的都很好,也說明了設計方法的有效性。在轉折處本文未嚴格按照NURBS的曲率設定錐形流尺度,而是使曲率逐漸過渡,這樣處理保證了過渡段的曲面光滑,但對乘波體的氣動性能有一定的影響。 表1 尖頭乘波體CFD氣動力驗證Table 1 CFD validation of the cusp waverider 2.3 激波角和后掠角的影響 考查激波角和后掠角對乘波體性能的影響。如未特別指出,設計狀態默認為H=30km,Ma=8。當Ma=8時馬赫角為7.18°,此為激波角的最小值,后掠角的上限為82.82°[11]。除了氣動性能,容積在飛行器設計中也必須考慮,一般定義容積率τ=V2/3/S為評價指標,V是容積,S為平面投影面積。 圖9給出了幾個不同后掠角組合乘波體的升阻比和容積率隨激波角的變化,設計參數ω=0.2,ζ=0。從圖9可以看出,升阻比在β=10°左右取得最大值,且隨β增大而降低;λ1越小同等激波角下的升阻比越大;容積率隨β增大而升高。圖9給出了升阻比-容積率關系,對于乘波體構型,容積率一般選擇在0.1以上,否則工程實用價值較低,當τ>0.1時,形成了類似于多目標優化中的Pareto前沿面,此時后掠角75~75°(λ1=75°,λ2=75°)組合的性能較好。 對于雙后掠乘波體外形,后掠角λ1和λ2對乘波體的性能都有影響,并且容積率受λ2影響很大。以圖9中的55-40°和75-50°外形為例,因為λ2較小,容積率甚至比51-45°和65-60°組合更低。 當固定λ2時,同等β下λ1越大,升阻比越小,容積率升高。圖10(a)為固定λ2=45°時的升阻比-容積率曲線,在τ>0.1時,形成Pareto前沿面,最優外形集在λ1較大時取得。 當固定λ1時,同等β下λ2越大,升阻比越小,但容積率升高。圖10(b)給出了固定λ1的升阻比-容積率曲線,最高點位置隨λ2的增大右移,Pareto前沿面直到τ>0.15才完全形成。在考慮升阻比-容積率的綜合性能時,可以適當減小λ2以獲得最優外形。 綜合圖9和圖10,修改后掠角不會對乘波體的氣動性能帶來質的減小,雖然容積率有所下降,但第一后掠角對應的機身部分保持不變,提供了主要的裝載空間,有效容積不會減小太多。 2.4 彎頭和后掠區域參數的影響 ζ控制彎頭區域的大小,當ζ接近0時,生成的外形是尖頭雙后掠乘波體,也被稱作渦升力乘波體[17]。當ζ>0時得到彎頭雙后掠外形。ζ(∈[0,1])大小表示彎頭程度。 圖11給出了ζ對升阻比的影響,隨著ζ增加,當β小于10°時,升阻比下降;在激波角大于10°時,升阻比增加。ζ對容積率影響很小。當激波角小于10°時,乘波體很薄,影響規律相反,這也與第2.3節中的分析相符,具體影響還要后續細致研究。 考查后掠區域控制參數ω對乘波體性能的影響,圖12給出了ω對升阻比的影響,隨著ω增加,升阻比下降(除β=8°外),此時容積率略微增加,對應第2.3節中的分析結果。 1) 密切錐乘波體設計中存在兩個重要的全域性幾何關系,據此提出定平面形狀乘波體概念,并重點分析了雙后掠外形。結合NURBS表達曲線輔助設計,提高了設計靈活性,保證曲面光滑,也方便提取設計變量。 2) 后掠角最大的乘波體外形處于升阻比和容積率較優的位置,隨激波角的增大升阻比先增大后減小,容積率逐漸增大;不同后掠角組合對升阻比和容積率都有影響,在考慮升阻比/容積率的綜合性能時,可以適當減小第二后掠角以獲得最優外形;升阻比隨彎頭度和后掠區域影響參數的變化趨勢與激波角和后掠角有關。 3) 考慮黏性的氣動力快速評估方法效率很高,本文通過CFD方法驗證了設計和評估方法的有效性。雙后掠乘波體保持了高超聲速狀態的性能優勢,后續工作中需進一步研究平面形狀對乘波體非設計點性能的影響,探索兼顧低速性能的乘波體氣動外形的設計方法。 [1] Nonweiler T R. Aerodynamic problems of manned space vehicles [J]. Journal of Royal Aeronautical Society, 1959, 63(1):521-530. [2] Jones J G, Moore K C, Pike J, et al. A method for designing lifting configurations for high supersonic speeds using axisymmetric flow field [J]. Archive of Applied Mechanics, 1968, 37(1): 56-72. [3] Rasmussen M L. Waverider configurations derived from inclined circular and elliptic cones [J]. Journal of Spacecraft and Rockets, 1980, 17(6): 537-545. [4] 劉傳振, 白鵬, 陳冰雁. 三維流場乘波體快速設計方法及多目標優化[J]. 宇航學報, 2016, 37(5): 535-543. [Liu Chuan-zhen, Bai Peng, Chen Bing-yan. Rapid desing and multi-object optimization for waverider from 3D flow[J]. Journal of Astronautics, 2016, 37(5) : 535-543.] [5] Marcu A L, Kojiro S. Experimental investigation of a Mach 3.5 waverider designed using computational fluid dynamics [J]. AIAA Journal, 2015, 53(6): 1590-1601. [6] Sobieczky H, Dougherty F C, Jones K. Hyper-sonic waverider design from given shock wave [C]. The First International Waverider Symposium, University of Maryland, MD, USA, 1990. [7] 王發民, 丁海河, 雷麥芳. 乘波布局飛行器寬速域氣動特性于研究[J]. 中國科學E輯: 技術科學, 2009, 39(11): 1828-1835. [Wang Fa-min, Ding Hai-he, Lei Mai-fang. Aerodynamic characteristics research on wide-speed range waverider configuration [J]. Sci China Ser E-Tech Sci, 2009, 39(11): 1828-1835.] [8] 賈子安, 張陳安, 王柯穆,等. 乘波布局高超聲速飛行器縱向靜穩定特性分析[J]. 中國科學E輯: 技術科學, 2014, 44: 1114-1122. [Jia Zi-an, Zhang Chen-an, Wang Ke-mu, et al. Longitudinal static stability analysis of hypersonic waveriders [J]. Sci China Ser E-Tech Sci, 2014, 44: 1114-1122.] [9] Starkey R, Lewis M. A Simple analytical model for parametric studies of hypersonic waveriders [C]. The 8th International Space Planes and Hypersonic Systems and Technologies Conference, Norfollk, VA, USA, Apr. 27-30, 1998. [10] Patrick E R. Geometrical relations for osculating cones and osculating flowfield waveriders [C]. The 49th Aerospace Science Meeting, Orlando, Florida, Jan. 4-7, 2011. [11] 段焰輝, 范召林, 吳文華. 定后掠角密切錐乘波體的生成和設計方法研究[J]. 航空學報, 2016, 37(10): 3023-3034. [Duan Yan-hui, Fan Zhao-lin, Wu Wen-hua. Research on the methods of generation and design of osculation cone waverider with constant angle of sweepback [J]. Acta Aeronoutica et Astronautica Sinica, 2016, 37(10): 3023-3034.] [12] Jones K D, Center K B. Waverider design methods for non-conical shock geometries [R]. The 3rd Theoretical Fluid Mechanics Meeting, St.Louis, Missouri, USA, June 24-26, 2002. [13] Les P, Wayne T. The NURBS Book, 2nd Edition[M]. Springer-Verlag, New York, 1997: 202-227. [14] 段焰輝. 高超聲速飛行器氣動外形優化設計方法研究[D]. 西安: 西北工業大學, 2013. [Duan Yan-hui. Research on methods of aerodynamic shape optimi-zation for hypersonic vehicles[D]. Xi'an: Northwestern Polytechnical University, 2013.] [15] Corda S, Anderson J. Viscous optimized hypersonic waveriders designed from axisymmetric flow fields [C]. The 26th Aerospace Sciences Meeting, Revo, NV, USA, Jan. 11-14, 1988. [16] Anderson J D. Fundamentals of aerodynamics [M]. The 3rd edition. McGraw-Hill Companies, USA, 2001. [17] Patrick E R. Vortex lift waverider configurations [C]. The 50th Aerospace Science Meeting, Knoxvell, Tennessee, USA, Jan. 9-12, 2012. 劉傳振(1989- ),男,博士生,主要從事飛行器氣動外形設計。 通信地址:北京7201信箱16分箱(100074) 電話:13161912959 E-mail: chuanzhenliu@gmail.com (編輯:牛苗苗) Analysis on Design Variables for Planform-Controllable Waverider LIU Chuan-zhen, BAI Peng, CHEN Bing-yan, ZHOU Wei-jiang (China Academy of Aerospace Aerodynamics, Beijing 100074, China) The concept of one planform-controllable waverider is proposed to extend the flexibility of the osculating waverider design. The universal geometry relations between the design and planform parameters are deducted, and employing the non-uniform rational B-spline in representing the design curve to aid design, the article builds the method of the double swept waverider generation in which the blunt area and swept area are controllable. The design variables are extracted to customize the planform of the waverider. The rapid aerodynamic assessment including viscous effect, validated with the CFD technique, is applied to analyze the influence of the design variables for waverider properties. The research shows that the hypersonic high L/D property of the waverider remains with the modified planform and lays the solid foundation to design the novel waverider configurations. Waverider; Planform-controllable; Double swept; Design Variables; Aerodynamic characteristics 2016-10-19; 2017-03-17 國家自然科學基金(11672281) TP731 A 1000-1328(2017)05-0451-08 10.3873/j.issn.1000-1328.2017.05.0022 設計變量影響分析
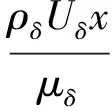
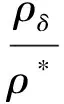
3 結 論

