燃?xì)鉁u輪發(fā)動機(jī)滑模參數(shù)限制調(diào)節(jié)系統(tǒng)設(shè)計分析

張園鎖，陶金偉，黃 瀏，張 哲，謝瑾瑜

（中國航發(fā)商用航空發(fā)動機(jī)有限責(zé)任公司，上海 200241）

燃?xì)鉁u輪發(fā)動機(jī)滑模參數(shù)限制調(diào)節(jié)系統(tǒng)設(shè)計分析

張園鎖，陶金偉，黃 瀏，張 哲，謝瑾瑜

（中國航發(fā)商用航空發(fā)動機(jī)有限責(zé)任公司，上海 200241）

設(shè)計了一種基于滑模控制的參數(shù)限制調(diào)節(jié)系統(tǒng)，能夠?qū)θ細(xì)鉁u輪發(fā)動機(jī)的燃油流量進(jìn)行調(diào)節(jié)確保其在全轉(zhuǎn)速范圍內(nèi)工作時候工作關(guān)鍵運(yùn)行參數(shù)限制內(nèi)。首先，基于滑模控制原理開展了滑模調(diào)節(jié)系統(tǒng)的結(jié)構(gòu)設(shè)計，該調(diào)節(jié)系統(tǒng)主要由主滑模調(diào)節(jié)器、限制參數(shù)滑模調(diào)節(jié)器和高低選選擇器組成；其次，基于通用的非線性渦輪發(fā)動機(jī)模型開展了模型辨識，獲取了在調(diào)節(jié)器設(shè)計點(diǎn)的線性模型；然后，基于線性模型證明了所設(shè)計的滑模調(diào)節(jié)系統(tǒng)的漸近穩(wěn)定性；最后，基于混合2-范數(shù)和無窮范數(shù)為優(yōu)化目標(biāo)獲取了反饋增益，并通過初步調(diào)試獲取了滿足過渡態(tài)時域控制指標(biāo)的滑模控制參數(shù)（邊界層厚度、切換增益）。基于如上設(shè)計的調(diào)節(jié)系統(tǒng)結(jié)果仿真表明：1）滑模非線性調(diào)節(jié)系統(tǒng)能夠保證渦輪發(fā)動機(jī)在全轉(zhuǎn)速內(nèi)的穩(wěn)態(tài)和過渡態(tài)控制品質(zhì)；2）所設(shè)計的滑模調(diào)節(jié)系統(tǒng)中參數(shù)限制調(diào)節(jié)器能夠在發(fā)動機(jī)過渡態(tài)過程中一直起作用，克服了線性調(diào)節(jié)傳統(tǒng)中參數(shù)限制調(diào)節(jié)器不能在過渡態(tài)過程中實施限制作用的弊端；3）采用滑模邊界層厚度參數(shù)可以抑制和消除滑模控制過程的控制量的“抖振”現(xiàn)象。

滑模；辨識；參數(shù)限制；調(diào)節(jié)系統(tǒng)；設(shè)計

0 引言

作為高復(fù)雜性航空動力系統(tǒng)，燃?xì)鉁u輪發(fā)動機(jī)部件眾多、機(jī)理復(fù)雜，而其核心機(jī)（主要包括壓氣機(jī)、燃燒室和渦輪三大部件）則以工作環(huán)境條件極其惡劣（高溫、高壓和高轉(zhuǎn)速）一向是發(fā)動機(jī)設(shè)計的重點(diǎn)，核心機(jī)的穩(wěn)定運(yùn)行直接決定了渦扇發(fā)動機(jī)的各種性能指標(biāo)和安全性指標(biāo)是否達(dá)到；同時，燃?xì)鉁u輪發(fā)動機(jī)以其工作轉(zhuǎn)速范圍內(nèi)高度的非線性對控制設(shè)計提出了很大的挑戰(zhàn)；如何設(shè)計出既能對運(yùn)行關(guān)鍵參數(shù)（高壓壓氣機(jī)、燃燒室和高壓渦輪的氣動熱力參數(shù)等）進(jìn)行限制保護(hù)同時又能夠兼顧穩(wěn)態(tài)推力及功率指標(biāo)、動態(tài)加速響應(yīng)的控制系統(tǒng)，一直是當(dāng)前動力裝置控制研究領(lǐng)域的前沿問題[1～4]。

參數(shù)限制及保護(hù)不僅關(guān)乎發(fā)動機(jī)的安全運(yùn)行，良好的參數(shù)限制更使得發(fā)動機(jī)壓氣機(jī)喘振裕度提升和熄火傾向減小，從而延長了發(fā)動機(jī)的壽命[5]。本文針對渦扇發(fā)動機(jī)核心機(jī)關(guān)鍵參數(shù)的限制保護(hù)設(shè)計了一種調(diào)節(jié)系統(tǒng)進(jìn)行了初步的設(shè)計和方針分析研究，此調(diào)節(jié)系統(tǒng)基于變結(jié)構(gòu)的滑動模型控制方法[6]。

滑模控制方法主要采用矩陣?yán)碚摵臀⒎謳缀螖?shù)學(xué)工具，滑模調(diào)節(jié)器的設(shè)計可避免針對被控對象的傳遞函數(shù)開展耗時的頻域整形迭代設(shè)計；且由于滑模控制以李亞普諾夫穩(wěn)定性定義為理論基礎(chǔ)，可針對非線性的被控對象直接開展調(diào)節(jié)器的設(shè)計，無需將被對象分段線性化后逐段設(shè)計線性調(diào)節(jié)器[7]。鑒于滑模控制此諸多的優(yōu)點(diǎn)，其已在工程領(lǐng)域被大量實踐和應(yīng)用，如飛機(jī)防滑剎車系統(tǒng)滑移率控制[8]，車輛跟車控制[9,10]，衛(wèi)星機(jī)動控制[11]，導(dǎo)彈制導(dǎo)控制[12]，永磁同步電機(jī)控制[13]，城市軌交地鐵停車控制[14]，內(nèi)燃機(jī)氣門升程控制[15]，混合動力汽車自適應(yīng)巡航控制[16]等。在滑模方法航空發(fā)動機(jī)控制應(yīng)用方面，國內(nèi)空軍工程大學(xué)的苗卓廣等人在模型預(yù)測滑模控制[17]、粒子群優(yōu)化網(wǎng)絡(luò)整定航空發(fā)動機(jī)全程滑模型控制[18]等方面開展了較為全面的探索和研究，國外的Hanz Richter在文獻(xiàn)[19]中也對滑模控制在航空發(fā)動機(jī)控制方面的應(yīng)用進(jìn)行了較為深入的論述和實踐。

本文所設(shè)計的滑模參數(shù)限制調(diào)節(jié)系統(tǒng)主要由滑模調(diào)節(jié)器、選擇器和積分器三大部分組成，作為調(diào)節(jié)系統(tǒng)核心的滑模型調(diào)節(jié)器為非線性調(diào)節(jié)器，相比傳統(tǒng)的基于“增益調(diào)度”的線性調(diào)節(jié)器為核心部件組成的線性參數(shù)限制調(diào)節(jié)系統(tǒng)，新的調(diào)節(jié)系統(tǒng)從理論層面克服了過渡態(tài)過程限制保護(hù)的不足，確保了在有限時間內(nèi)達(dá)到限制值，且避免了不同調(diào)節(jié)器之間不停切換導(dǎo)致的不穩(wěn)定現(xiàn)象。雖然滑模型控制方法有如上諸多優(yōu)點(diǎn)，但由于滑模控制本質(zhì)上是一種非線性控制，其不可避免地會引入控制的不連續(xù)性，即常見的滑模調(diào)節(jié)器輸出的控制量“抖振”的現(xiàn)象，本文中也針對滑模調(diào)節(jié)器非線性的特點(diǎn)，對非線性進(jìn)行了近似處理，在一定程度上抑制了滑模非線性調(diào)節(jié)器固有的“抖振”，同時達(dá)到了對被控對象關(guān)鍵運(yùn)行參數(shù)限制的目的。

1 滑模調(diào)節(jié)系統(tǒng)設(shè)計

通用的燃?xì)鉁u輪發(fā)動機(jī)參數(shù)限制保護(hù)調(diào)節(jié)器調(diào)節(jié)目標(biāo)將發(fā)動機(jī)從任意初始穩(wěn)態(tài)點(diǎn)控制到另一個穩(wěn)定的目標(biāo)穩(wěn)態(tài)點(diǎn)兩個穩(wěn)態(tài)點(diǎn)之間的過渡控制過程中，如果被限制參量未達(dá)到其限制值則發(fā)動機(jī)轉(zhuǎn)速可達(dá)到，若控制過程觸及被限變量，則發(fā)動機(jī)狀態(tài)則穩(wěn)定在此限制值。傳統(tǒng)線性調(diào)節(jié)器通過各個被控或被限變量形成的單輸入單輸出（SISO）回路計算的控制指令進(jìn)行高低選來實現(xiàn)，高低選邏輯的復(fù)雜性導(dǎo)致其穩(wěn)定性不能保證，過渡態(tài)時被限制參數(shù)經(jīng)常出現(xiàn)超限，限制回路提前搶占主控回路控制權(quán)等現(xiàn)象，導(dǎo)致實際的參數(shù)限制管理功能、性能達(dá)不到指標(biāo)要求[5]。

1.1 滑模調(diào)節(jié)系統(tǒng)結(jié)構(gòu)設(shè)計

本文設(shè)計了一種滑模參數(shù)限制非線性調(diào)節(jié)系統(tǒng)，本調(diào)節(jié)系統(tǒng)主要由非線性調(diào)節(jié)器[20]（主滑模調(diào)節(jié)器、滑模限制調(diào)節(jié)器）、選擇器、積分器和線性被控對象模型組成，系統(tǒng)架構(gòu)如圖1所示。

滑模參數(shù)限制調(diào)節(jié)系統(tǒng)的具體設(shè)計過程如下。

1.1.1 對象模型設(shè)計

本文研究的被控對象為單軸的燃?xì)鉁u輪發(fā)動機(jī)，其主控制輸入為燃油流量（Wf），主被控輸出為軸轉(zhuǎn)速N1，被限制參數(shù)為壓氣機(jī)出口靜壓和總溫（P3、T3）、渦輪排氣總溫（EGT）；選擇N1為狀態(tài)量，在發(fā)動機(jī)模型某穩(wěn)態(tài)點(diǎn)附近區(qū)域，可用如下簡化的線性狀態(tài)空間模型來近似描述。

式(1)、式(2)中X=ΔN2為調(diào)節(jié)系統(tǒng)受控對象模型的狀態(tài)變量， 為調(diào)節(jié)系統(tǒng)受控對象模型的輸入變量，為調(diào)節(jié)系統(tǒng)受控對象模型輸出，K為4×1維調(diào)節(jié)系統(tǒng)受控對象狀態(tài)輸出矩陣，Θ為4×1維調(diào)節(jié)系統(tǒng)受控對象輸入輸出矩陣。

滑模調(diào)節(jié)系統(tǒng)的設(shè)計需要基于被控對象的穩(wěn)態(tài)特性工作線，本文所設(shè)計的調(diào)節(jié)系統(tǒng)的被控對象為通用的燃?xì)鉁u輪發(fā)動機(jī)非線性模型，且滿足如下的非線性離散數(shù)學(xué)關(guān)系式。

圖1 滑模參數(shù)限制調(diào)節(jié)系統(tǒng)控制架構(gòu)

對發(fā)動機(jī)的燃油輸入Wf作小階躍擾動則控制量Wf滿足下式。

狀態(tài)量N2(k)和輸出量Y(k)的序列值均由(3)獲取為已知，根據(jù)最小二乘擬合思想，直接建立如式(6)的最小二乘問題模型。

由(6)所獲取的 既可以保證子在穩(wěn)態(tài)點(diǎn)附近待擬合線性系統(tǒng)符合最小二乘意義下的最小化。由式(3)、式(5)、式(6)獲取式(4)系數(shù)過程，鑒于各變量原始數(shù)值（式(3)驅(qū)動下狀態(tài)變量和輸出變量序列數(shù)值）之間相差數(shù)個數(shù)量級，可以基于穩(wěn)態(tài)點(diǎn)數(shù)值對方程(4)中離散變量進(jìn)行歸一化，在此不再贅述此歸一化過程的數(shù)學(xué)變換，詳細(xì)的非線性模型辨識線性模型的方法可參閱文獻(xiàn)[21]。

基于如上小階躍方法的線性化辨識結(jié)果式(7)慢車附近狀態(tài)起始點(diǎn)系數(shù)矩陣，式(8)最大推力附近狀態(tài)起始點(diǎn)系數(shù)矩陣。

1.1.2 積分器設(shè)計

本文設(shè)計調(diào)節(jié)系統(tǒng)為保證被控或被限變量無穩(wěn)態(tài)誤差，對被控對象輸入使用了積分環(huán)節(jié)，引入式(9)中間變量Ur，即為待設(shè)計的調(diào)節(jié)器輸出。

1.1.3 調(diào)節(jié)器設(shè)計

針對如式(1,2)描述的發(fā)動機(jī)模型，設(shè)計如下滑模量：

系統(tǒng)達(dá)到滑模態(tài)時滿足如下方程：

根據(jù)李亞普諾夫第二方法[22,23]，若能夠找到一個標(biāo)量李亞普諾夫函數(shù)，使函數(shù)滿足三個李亞普諾夫條件：1）李亞普諾夫函數(shù)正定；2）李亞普諾夫函數(shù)的導(dǎo)數(shù)負(fù)定；3）且當(dāng)函數(shù)變量趨近無窮時，李雅普諾夫函數(shù)亦趨近于無窮，則可以判定說設(shè)計的系統(tǒng)全局漸收斂于平衡狀態(tài)點(diǎn)。本文基于如上定義的滑模量，選擇的李亞普諾夫函數(shù)如下[20,22]。

容易知道，下式子成立。

圖2 滑模參數(shù)限制調(diào)節(jié)系統(tǒng)主滑模調(diào)節(jié)器控制原理

圖3 滑模參數(shù)限制調(diào)節(jié)系統(tǒng)限制滑模調(diào)節(jié)器控制原理

即，李亞普諾夫的在平衡狀態(tài)點(diǎn)時為零，其他狀態(tài)大于零；且隨著狀態(tài)量遠(yuǎn)離平衡點(diǎn)趨向于無窮遠(yuǎn)時候李亞普諾夫函數(shù)亦趨近于無窮。

為保證在有限時間內(nèi)系統(tǒng)從任意初始平衡狀態(tài)達(dá)到滑模穩(wěn)定狀態(tài)，下面的李亞普諾夫?qū)?shù)條件式子必須成立。

為滿足式(16)要求，選取等速指數(shù)衰減的趨近律[19,20]，只需要式(17)成立即可：

式(17)中η為某一恒定正數(shù)，其反映了滑模變量S收斂于目標(biāo)滑模面穩(wěn)態(tài)點(diǎn)切換運(yùn)動特性的常數(shù)，即切換增益系數(shù)，假設(shè)系統(tǒng)從初始點(diǎn)經(jīng)由時間tr到達(dá)滑模態(tài)，即S(tr)=0，對式(17)進(jìn)行積分，結(jié)果如式(18)所示。

考慮如式(17)滑模量運(yùn)行滿足指數(shù)衰減趨近規(guī)律，要求系統(tǒng)運(yùn)動達(dá)到穩(wěn)態(tài)滑模面過程中滑模量S符號不變（保證系統(tǒng)在滑模運(yùn)動過程單調(diào)趨近零的特性），因此式(18)可轉(zhuǎn)換為式(19)。

聯(lián)立式(1)、式(2)、式(10)、式(11)、式(17)可得式(20)成立，寫成分量形。

考慮上面式(17)中連續(xù)的滑模變量Si會有無限多次通過零點(diǎn)，對Si進(jìn)行數(shù)值積分不可行，式(20)且獲取的控制量具有跳躍性質(zhì)，實際工程控制的作動機(jī)構(gòu)無法完成此種跳變執(zhí)行任務(wù)，且即使在仿真環(huán)境也對數(shù)值積分結(jié)算器的很大挑戰(zhàn)。鑒于符號函數(shù)的引入會對滑模運(yùn)動過程產(chǎn)生“抖振”的控制現(xiàn)象[24,25]，本文采用如下的飽和函數(shù)近似代替符號函數(shù)來描述滑模變量Si的漸近趨近特性[19,20]，并同時抑制滑模運(yùn)動的抖振現(xiàn)象，符號函數(shù)的處理如式(21)所示。

上式中正常數(shù)φ反映滑變量切換的邊界，簡稱為邊界層厚度。

1.1.4 選擇器設(shè)計

設(shè)計低選-高選選擇律為：

式(22)中，L={1，2，…，l}且H={1，2，…，h}，Urzj是與低選選擇器相聯(lián)接的滑模參數(shù)限制調(diào)節(jié)器輸出，Urzk為高選選擇器相聯(lián)接的滑模參數(shù)限制調(diào)節(jié)器輸出，主滑模調(diào)節(jié)器輸出直接默認(rèn)連接在低選器上，其輸出為Ur1。

基于文獻(xiàn)中論證限制保護(hù)的不變性特性選取器關(guān)聯(lián)準(zhǔn)則[20,26]，可將不同的調(diào)節(jié)器輸出Ur分配到相應(yīng)的選擇器上面,保證所設(shè)計調(diào)節(jié)系統(tǒng)的參數(shù)限制功能，具體設(shè)計的高低選設(shè)計結(jié)果如表1和圖4所示。

表1 滑模調(diào)節(jié)器低選-高選選擇器設(shè)計結(jié)果

圖4 滑模控制量高低選調(diào)節(jié)器原理圖

1.2 滑模調(diào)節(jié)系統(tǒng)參數(shù)設(shè)計

本節(jié)主要對本文設(shè)計的滑模參數(shù)限制調(diào)節(jié)系統(tǒng)中由式(2)描述的輸出變量系數(shù)矩陣進(jìn)行求解。本文設(shè)計的滑模參數(shù)限制調(diào)節(jié)系統(tǒng)的中被控對象可簡化為單輸入多輸出（SIMO）模型，輸入變量為Wf，輸出變量為N2、壓氣機(jī)出口溫度T3和靜壓P33、排氣溫度EGT，且被控輸出變量設(shè)計點(diǎn)隨著發(fā)動機(jī)初始穩(wěn)態(tài)推力狀態(tài)不同而改變。

參數(shù)限制變量（T3，EGT和Ps3）的Ki和Θi（i=2，3，4）由初始系統(tǒng)穩(wěn)態(tài)點(diǎn)對應(yīng)的被控對象線性狀態(tài)空間模型對應(yīng)的輸出矩陣確定，且Θ1也通過線性狀態(tài)空間模型確定。

本部分基于狀態(tài)反饋控制律對滑模調(diào)節(jié)系統(tǒng)中被控對象控制量U=Wf進(jìn)行了設(shè)計[27,28]，即如式(23)所示。

描述調(diào)節(jié)系統(tǒng)在滑模控制起始穩(wěn)態(tài)點(diǎn)附近的線性模型狀態(tài)方程如式(1)和性能輸出方程如式(24)、(25)所示。

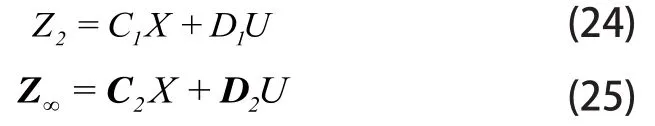
將式(23)代入式(2)、式(24)、式(25)可獲取式(26)、式(27)、式(28)所示：

分別對式(26)、式(27)、式(28)進(jìn)行拉氏變換并聯(lián)立的式(29)、式(30)。

其中GU,Z2為發(fā)動機(jī)模型輸入U到性能輸出Z2的傳遞函數(shù)；GU,Z∞為發(fā)動機(jī)模型輸入U到性能輸出Z∞的傳遞函數(shù)。

本文采用帶有混合H2/H∞范數(shù)優(yōu)化的區(qū)域極點(diǎn)配置方法對參數(shù)K進(jìn)行尋優(yōu)設(shè)計，采用2-范數(shù)和無窮范數(shù)加權(quán)表示優(yōu)化目標(biāo)，即采用式(31)設(shè)計目標(biāo)，尋求使被控對象輸Wf到輸出（T3、EGT和Ps3）混合范數(shù)M最小的反饋增益K。

上式中，a和b是非負(fù)的權(quán)重值，本設(shè)計中a=0.5和b=0.5，表明H2和HH∞優(yōu)化目標(biāo)的權(quán)重相同。

本文設(shè)計的滑模調(diào)節(jié)系統(tǒng)反饋增益K以發(fā)動機(jī)地面慢車附近狀態(tài)點(diǎn)和最大推力附近狀態(tài)點(diǎn)的線性模型為基準(zhǔn)，設(shè)計結(jié)果表示如式(32)所示，式中為主滑模輸入調(diào)節(jié)系數(shù)。

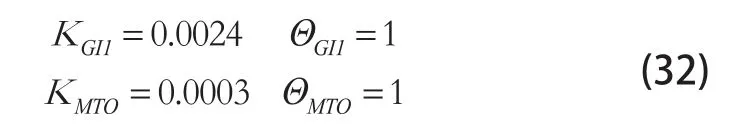
對狀態(tài)變量N2的反饋控制律的反饋增益矩陣K的設(shè)計過程進(jìn)行了說明，滑模控制參數(shù)限制管理調(diào)節(jié)器的可調(diào)參數(shù)為Φ和η，此兩變量用于對算例仿真過程滑模量響應(yīng)進(jìn)行調(diào)整確定[20]。

1.3 滑模調(diào)節(jié)系統(tǒng)穩(wěn)定性設(shè)計

本部分主要對滑模參數(shù)限制調(diào)節(jié)系統(tǒng)架構(gòu)的穩(wěn)定性進(jìn)行初步的證明，證明本文設(shè)計的系統(tǒng)在全局漸近穩(wěn)定，同時保證在有限時間內(nèi)達(dá)到限制值而不超限。

工程上常用的發(fā)動機(jī)線性調(diào)節(jié)系統(tǒng)穩(wěn)定性設(shè)計基于李亞普諾夫第一方法[23,29,30]，即如果非線性被控模型微偏線性化后，獲取的線性系統(tǒng)特征多項式全部極點(diǎn)均在左半平面，則可判定原來非線性系統(tǒng)是穩(wěn)定的。本文設(shè)計的調(diào)節(jié)系統(tǒng)基于李亞普諾夫第二方法，如利用前面式(13)表示的李亞普諾夫函數(shù)，可知，李亞普諾夫第二法要求的兩個條件已經(jīng)滿足，僅需保證式(17)成立即可證明所設(shè)計的滑模參數(shù)限制調(diào)節(jié)系統(tǒng)穩(wěn)定。

式(17)的詳細(xì)的論證過程此文不做直接證明，具體細(xì)節(jié)可參考文獻(xiàn)[20]，本文直接引用此篇文獻(xiàn)中的定理12，若保證下面三個條件成立，即可保證本文設(shè)計的滑模參數(shù)限制調(diào)節(jié)系統(tǒng)是全局漸近穩(wěn)定。

A為非奇異矩陣；

式(20)控制輸入經(jīng)由式(22)選擇律選擇后，式(1)和式(2)表示的被控對象運(yùn)行軌跡在有限的時間內(nèi)漸近收斂于唯一的平衡點(diǎn)X。

在GI1和MTO兩個起始穩(wěn)態(tài)點(diǎn)，由式(7)、式(8)、式(32)數(shù)據(jù)驗證，上面兩個條件均滿足，即本文設(shè)計的滑模參數(shù)限制調(diào)節(jié)系統(tǒng)全局漸近穩(wěn)定。

2 仿真試驗及分析

2.1 滑模調(diào)節(jié)器建模說明

本部分主要基于本文2.2節(jié)滑模參數(shù)限制調(diào)節(jié)器設(shè)計原理進(jìn)行了建模，其主要包括主滑模調(diào)節(jié)器設(shè)計建模、限制保護(hù)滑模調(diào)節(jié)器設(shè)計建模、滑模控制量低選-高選選擇器設(shè)計建模和調(diào)節(jié)器綜合建模等，具體結(jié)果如下：

基于圖2主滑模調(diào)節(jié)器控制原理，本文設(shè)計的主滑模調(diào)節(jié)器如圖5所示。

由圖3受限輸出滑模調(diào)節(jié)器控制原理，設(shè)計受限變量（EGT示例）滑模調(diào)節(jié)器如圖6所示。

由滑模主調(diào)節(jié)器、滑模受限輸出調(diào)節(jié)器、低選-高選選擇器、積分器和控制對象組成的調(diào)節(jié)系統(tǒng)動態(tài)仿真模型如圖7所示。

2.2 滑模調(diào)節(jié)器仿真及分析

本文采用通用渦扇發(fā)動機(jī)核心機(jī)的實時非線性模型，分別采用如上所設(shè)計的滑模非線性參數(shù)限制調(diào)節(jié)系統(tǒng)和傳統(tǒng)的增益可調(diào)線性參數(shù)限制調(diào)節(jié)系統(tǒng)對模型進(jìn)行了控制仿真。

仿真環(huán)境采用5ms定步長模型，仿真模型主要基于如上所設(shè)計的滑模參數(shù)限制調(diào)節(jié)系統(tǒng)和非線性發(fā)動機(jī)模型，組成包括非線性滑模調(diào)節(jié)器（主滑模調(diào)節(jié)器、參數(shù)限制滑模調(diào)節(jié)器）、高-低選選擇器、滑模控制量積分器、非線性發(fā)動機(jī)模型和指令模塊組成，詳細(xì)結(jié)構(gòu)如圖8所示。其中發(fā)動機(jī)模型輸入接口被封裝為單燃油流量輸入簡化模型，輸出包括N2（核心機(jī)轉(zhuǎn)速）、T3（高壓壓氣機(jī)出口總溫）、EGT（高壓渦輪出口總溫）和Ps3（高壓壓氣機(jī)出口靜壓）。

本文模擬了發(fā)動機(jī)從GI1（地面慢車）附近推力狀態(tài)到MTO（最大起飛）附近推力狀態(tài)，然后再回到GI2附近推力狀態(tài)的參數(shù)限制管理仿真試驗。

圖5 主滑模調(diào)節(jié)器仿真框圖

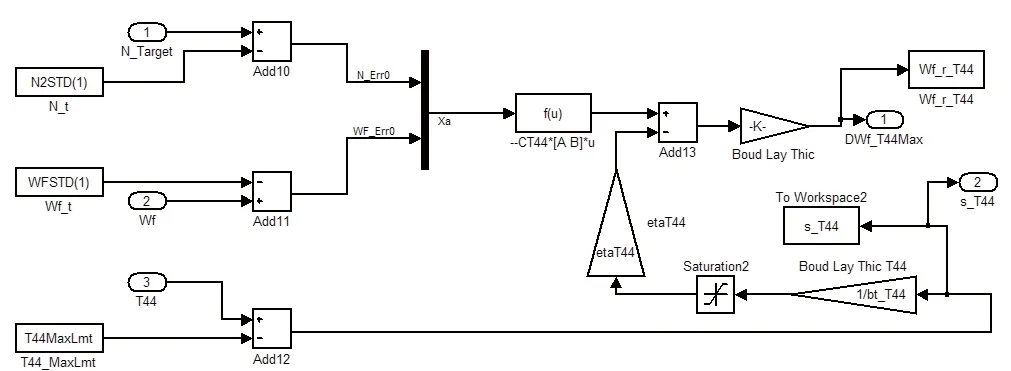
圖6 受限輸出滑模調(diào)節(jié)器仿真框圖

圖7 滑模參數(shù)限制動態(tài)調(diào)節(jié)系統(tǒng)控制原理圖

圖8 滑模參數(shù)限制動態(tài)調(diào)節(jié)系統(tǒng)仿真框圖

仿真的發(fā)動機(jī)模型設(shè)置為地面靜止標(biāo)準(zhǔn)海平面條件：高度H=0m，馬赫數(shù)Ma=0且標(biāo)準(zhǔn)溫差DT=0。常規(guī)燃?xì)鉁u輪發(fā)動機(jī)從地面慢車推力至最大推力再返回值地面慢車過程，均需要將發(fā)動機(jī)設(shè)計成不僅達(dá)到推力和功率指標(biāo)（N2目標(biāo)值為衡量推力和功率是否達(dá)到的標(biāo)準(zhǔn)）而且此過程不會超出各參數(shù)的設(shè)計限制值，本發(fā)動機(jī)及其模型運(yùn)行同樣滿足這種要求。因此，考慮到演示參數(shù)限制的目的，本數(shù)字仿真試驗下調(diào)設(shè)置最大Ps3限制值為Ps3max=2000kPa、最大T3限制值為T3max=1000K、最大EGT限制值為EGTmax=1350K和最小Ps3限制值為Ps3min=1200kPa。

下面是仿真試驗結(jié)果的分析過程，其中圖12和圖13中的狀態(tài)參數(shù)響應(yīng)采用歸一化模式，相關(guān)的參數(shù)定義為：T3_r=T3/T3max，Ps3_r=Ps3/Ps3max，EGT_r=EGT/EGTmax，N2_r=N2/N2,D（其中，N2,D為本仿真發(fā)動機(jī)設(shè)計點(diǎn)轉(zhuǎn)速）。

圖9 滑模控制參數(shù)限制管理仿真測試用例

圖10 N2主控回路和Ps3最小值限制回路滑函數(shù)變化

圖11 T3、EGT和Ps3最大值限制回路滑變量變化

圖12 滑模控制參數(shù)限制動態(tài)調(diào)節(jié)系統(tǒng)的參數(shù)（歸一化）響應(yīng)

由圖10，圖11滑函數(shù)的變化曲線可知，本文設(shè)計的滑模型調(diào)節(jié)器（包括主滑模調(diào)節(jié)器、參數(shù)限制滑模調(diào)節(jié)器）在對發(fā)動機(jī)進(jìn)行控制過程無明顯的“抖振”想象，由滑模量計算得出的燃油控制量可以直接作為燃油計量機(jī)構(gòu)的期望并有伺服控制器執(zhí)行實時的閉環(huán)控制任務(wù)。

綜合圖10，圖11，圖12仿真結(jié)果可知：在加速過程，加速開始5s左右，相對T3和EGT最大限制值，Ps3最大限制值最先達(dá)到（Ps3_r=1）且Ps3最大值參數(shù)限制調(diào)節(jié)器的滑變量s_Ps3max同時達(dá)到0，即加速過程達(dá)到S_ Ps3max=0滑模穩(wěn)定狀態(tài)；T3和EGT最大值限制回路未達(dá)到限制值，其滑函數(shù)s_T3max和s_EGTmax分別從S_ T3max(0)=-289.6及S_EGTmax(0)=-414.0向值為0的方向移動，加速過程結(jié)束時仍未到達(dá)各自的滑模態(tài)。在減速過程，減速開始5s左右S_Ps3min=0達(dá)到0，即Ps3最小值限制回路達(dá)到（Ps3_r= Ps3min/ Ps3man=0.6），即減速過程達(dá)到s_Ps3min=0的滑模穩(wěn)定狀態(tài)。

圖13 線性調(diào)節(jié)器參數(shù)限制動態(tài)調(diào)節(jié)系統(tǒng)的參數(shù)（歸一化）響應(yīng)

圖13為基于增益調(diào)度的線性調(diào)節(jié)器參數(shù)限制動態(tài)調(diào)節(jié)系統(tǒng)仿真響應(yīng)，與圖12滑模控制參數(shù)限制動態(tài)調(diào)節(jié)系統(tǒng)相同的測試用例。

由圖13可知，在從慢車狀態(tài)至最大起飛推力狀態(tài)的加速過程中，線性調(diào)節(jié)器前期控制效果較為“陡”后期較過于“緩慢”，導(dǎo)致整體加速調(diào)整的時間較慢達(dá)到8s左右，這和EGT最大值線性調(diào)節(jié)器過早搶占加速調(diào)節(jié)器并由其主控整個加速調(diào)節(jié)過程有直接關(guān)系，而線性限制調(diào)節(jié)器的調(diào)節(jié)時間通常較主控調(diào)節(jié)器長；滑模調(diào)節(jié)器的加速調(diào)整時間約5s左右，且滑模過程EGT滑模調(diào)節(jié)器受限突破零值，迅速回調(diào)后較快地過阻尼單調(diào)趨近零值S_ EGT=0，達(dá)到滑模穩(wěn)定狀態(tài)，即由EGT限制值確定的發(fā)動機(jī)穩(wěn)定狀態(tài)。

在從最大起飛狀態(tài)至慢車狀態(tài)的減速過程中，同樣，線性調(diào)節(jié)器前期控制效果較為“陡”后期較過于“緩慢”，導(dǎo)致整體加速調(diào)整的時間較慢達(dá)到7s左右，這和Ps3最小值線性調(diào)節(jié)器過早搶占減速調(diào)節(jié)器并由其主控整個減速調(diào)節(jié)過程有直接關(guān)系，而線性參數(shù)限制調(diào)節(jié)器的調(diào)節(jié)時間通常較主控調(diào)節(jié)器長；滑模調(diào)節(jié)器的減速調(diào)整時間約5s左右，且滑模過程Ps3滑模調(diào)節(jié)器受限突破零值后輕微超調(diào)，迅速回調(diào)后很快地過阻尼單調(diào)趨近零值S_Ps3min=0，達(dá)到滑模穩(wěn)定狀態(tài)，即由EGT限制值確定的發(fā)動機(jī)穩(wěn)定狀態(tài)。

3 結(jié)束語

由本文的數(shù)字仿真試驗可知，相對傳統(tǒng)的基于參數(shù)自適應(yīng)調(diào)度的線性調(diào)節(jié)器，滑模控制在航空發(fā)動機(jī)上的應(yīng)用具有如下五個方面的優(yōu)點(diǎn)：

1）滑模控制調(diào)節(jié)系統(tǒng)得的設(shè)計過程不需要分段線性化，只需根據(jù)發(fā)動機(jī)的穩(wěn)態(tài)特性圖（滑模起始點(diǎn)狀態(tài)空間模型）即可設(shè)計；

2）控制參數(shù)的設(shè)計采用區(qū)域極點(diǎn)配置的混合H2/ Hinf綜合范數(shù)優(yōu)化算法，滑模調(diào)節(jié)器參數(shù)對被控模型參數(shù)變化的具有較強(qiáng)的魯棒性，且確保了在大范圍過渡態(tài)控制過程，以混合過程控制指標(biāo)最小化準(zhǔn)則保證了整個控制過渡過程品質(zhì)；

3）滑模控制在主控回路和受限回路的控制指令高低選原則清晰，且滑模調(diào)節(jié)器可保證所設(shè)計系統(tǒng)的全局漸近穩(wěn)定性，相比傳統(tǒng)線性調(diào)節(jié)器中對各回路計算的控制量進(jìn)行解耦選擇的復(fù)雜邏輯特性，大大降低了調(diào)節(jié)系統(tǒng)內(nèi)部邏輯設(shè)計的復(fù)雜度而又不損失調(diào)節(jié)系統(tǒng)的各種性能指標(biāo)；

4）過渡態(tài)度無需設(shè)計相應(yīng)的控制器，過渡態(tài)主要有滑模參數(shù)限制調(diào)節(jié)器完成，克服了傳統(tǒng)線性調(diào)節(jié)系統(tǒng)中線性參數(shù)限制調(diào)節(jié)器在發(fā)動機(jī)過渡態(tài)過程無法起作用的弊端[4,19]；

5）滑模調(diào)節(jié)器參數(shù)的設(shè)計過程直接對標(biāo)時域指標(biāo)，通過調(diào)整η和Φ可分別對控制過程調(diào)節(jié)時間和調(diào)節(jié)器輸出“抖振”進(jìn)行調(diào)校，相比根軌跡圖解法、頻響法、狀態(tài)空間法[27,28,30,31]設(shè)計調(diào)節(jié)參數(shù)能極大縮短迭代調(diào)試工作量。

鑒于滑模控制方法具有全局漸近穩(wěn)定性、過渡控制性能品質(zhì)最優(yōu)化、參數(shù)限制保護(hù)功能良好、調(diào)節(jié)器器設(shè)計調(diào)試簡單等方面的優(yōu)點(diǎn)，后續(xù)進(jìn)一步優(yōu)化本文所設(shè)計的滑模調(diào)節(jié)系統(tǒng)的架構(gòu)，融入隨發(fā)動機(jī)狀態(tài)和飛行環(huán)境條件變換的線性發(fā)動機(jī)模型，開展全飛行包線范圍內(nèi)的滑模參數(shù)限制調(diào)節(jié)仿真；另外，逐步開展離散時間滑模調(diào)節(jié)器設(shè)計，并嘗試通過發(fā)動機(jī)電子控制器（EEC）驗證設(shè)計的離散滑模算法[32]，嘗試與線性調(diào)節(jié)器綜合后驗證，逐步提升滑模控制在燃?xì)鉁u輪發(fā)動機(jī)推力控制和參數(shù)限制中的成熟度及應(yīng)用價值。

[1] 樊思齊.航空發(fā)動機(jī)控制[M].西北工業(yè)大學(xué)出版社,2008.

[2] 姚華.航空發(fā)動機(jī)全權(quán)限數(shù)字電子控制系統(tǒng)[M].航空工業(yè)出版社,2014.

[3] 孫建國,黃金泉,等.現(xiàn)代航空動力裝置控制[M].航空工業(yè)出版社,2009.

[4] 黃開明,尹澤勇,黃金泉.參數(shù)限制對渦軸發(fā)動機(jī)過渡態(tài)控制的影響[J].航空動力學(xué)報,2006,21(2)：432-436.

[5] Link C. Jaw, Jack D. Mattingly, Aircraft engine controls design, System Analysis, and Health Monitoring[M].Virginia (USA)：AIAA,2009.

[6] 劉金琨,孫富春.滑模變結(jié)構(gòu)控制理論及其算法研究與進(jìn)展[J].控制理論與應(yīng)用,2007,24(3)：407-418.

[7] 李殿璞.非線性控制系統(tǒng)理論基礎(chǔ)(第二版)[M].北京：清華大學(xué)出版社,2014.

[8] 付龍飛,田廣來,王鵬,等.飛機(jī)防滑剎車系統(tǒng)滑移率自適應(yīng)滑模控制研究[J].西北工業(yè)大學(xué)學(xué)報,2015,33(5)：770-774.

[9] 施繼忠,張繼業(yè),徐曉惠,胡永舉.隨機(jī)干擾的車輛跟隨系統(tǒng)滑模控制[J].西南交通大學(xué)學(xué)報,2015,50(6)：1088-1093.

[10] Shengbo Eben Li, Kun Deng, Keqing Li. Terminal sliding control of automated car following system without reliance on longitudinal acceleration information[J].Mechatronics,2015,30(9)：327-337.

[11] 常琳,孫金光,范國偉,徐開.基于terminal滑模控制的小衛(wèi)星機(jī)動方法[J].光學(xué)精密工程,2015,23(2)：485-496.

[12] 齊輝,張澤,韓鵬鑫,等.基于反演滑模控制的導(dǎo)彈制導(dǎo)控制一體化設(shè)計[J].系統(tǒng)工程與電子技術(shù),2016,38(3)：618-623.

[13] 王志宏,王翔,吳益飛,等.基于特征模型的PMSM調(diào)速系統(tǒng)離散自適應(yīng)滑模控制[J].南京理工大學(xué)學(xué)報,2015,39(6)：637-642.

[14] 王青元,吳鵬,馮曉云,張彥棟.基于自適應(yīng)終端滑模控制的城軌列車精確停車算法[J].鐵道學(xué)報,2016,38(2)：56-63.

[15] Mohammad Pournazeri,Amir Khajepour. Precise lift control in a new variable valve actuation system using discrete-time sliding mode control[J].Mechanism and Machine Theory,99.217-235(2016).

[16] Behnam Ganji,Abbas Z.kouzani, SuiYang Khoo. Adaptive cruise control of a HEV using sliding mode control[J].Expert system with applications,2014,41(2)：607-615.

[17] 苗卓廣,謝壽生,王磊,等.航空發(fā)動機(jī)多模型預(yù)測滑模控制[J].推進(jìn)技術(shù),2012,33(3).

[18] 苗卓廣,謝壽生,何秀然,等.自適應(yīng)PSO網(wǎng)絡(luò)整定的航空發(fā)動機(jī)全程滑模控制[J].推進(jìn)技術(shù),2011,32(3).

[19] Hanz Richter.Advanced Control of Turbofan Engines[M]. Springer. USA.2011.

[20] H.Richter. A multi-regulator sliding mode control strategy for output-constrained systems[J].Automatica 47.2251-2259(2011).

[21] 陸軍,郭迎清,陳小磊.線性擬合法建立航空發(fā)動機(jī)狀態(tài)變量模型[J].航空動力學(xué)報,2011,26(5)：1172-1177.

[22] Michael S. Branicky, Multiple Lyapunov Functions and Other Analysis Tools for Switched and Hybrid Systems[J].IEEE TRANSACTIONS ON AUTOMATIC CONTROL,1998,43(3)：475-482.

[23] 吳麒,王詩宓,杜繼宏,等.自動控制原理[M].2版.清華大學(xué)出版社,2006.

[24] Kang Hongbo, Shen Yu.On limit cycle chattering in sliding mode control systems under the influence of sampling intervals based on describing function approach[J].The Journal of China Universities of Posts and Telecommunications,2016,22(1)：55-59.

[25] Yuanyuan Zhang, Renfu Li, Tao Xue, Zhimin Liu, Zongxin Yao, An analysis of the stability and chattering reduction of highorder sliding mode tracking control for a hypersonic vehicle[J]. Information Sciences,2016,348(1)：25-48.

[26] F. Blanchini, Set invariance in control[J].Automatica,1998,35：1747-1767.

[27] Gene F.Franklin, J.David Powell, Abbas Emami-Naeini.自動控制原理與設(shè)計[M].6版.電子工業(yè)出版社,2014.

[28] R.Dorf, R. Bishop.現(xiàn)代控制系統(tǒng)[M].12版.電子工業(yè)出版社,2013.

[29] H.K. Khalil. Nonlinear Systems (Third Edition) [M].USA：Prentice-Hall Inc.,2002.

[30] 胡壽松.自動控制原理[M].6版.科學(xué)出版社,2013.

[31] Karl Johan Astrom, T. Hagglund, PID controllers： theory,design and tuning[M].Pennsylvania(USA)：Instrument Society of America,1995.

[32] Gene F.Franklin, J.David Powell, Michael Workman. Digital Control of Dynamic Systems(Third Edtion)[M].USA：Addison-Wesley,1998.

Design and analysis of parameter limit regulating system based on sliding mode control in gas turbine engine

ZHANG Yuan-suo, TAO Jin-wei, HUANG Liu, ZHANG Zhe, XIE Jin-yu

V233.7

：A

：1009-0134(2017)05-0022-09

2016-11-01

張園鎖（1983 -），男，河南人，碩士，研究方向為航空燃?xì)鉁u輪發(fā)動機(jī)控制系統(tǒng)工程設(shè)計、控制理論及算法的工程應(yīng)用的設(shè)計與驗證、控制系統(tǒng)軟件設(shè)計與驗證。