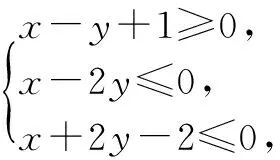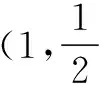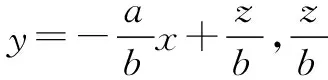全國卷數學高考必考的五種題型
甘肅省康縣教育局教研室(746500)
杜紅全●
全國卷數學高考必考的五種題型
甘肅省康縣教育局教研室(746500)
杜紅全●
縱觀近幾年全國卷的數學高考題,發現必考的有五種題型,供高考復習時參考.
一、與集合有關的題型
例1(2016全國Ⅲ卷,理1)設集合S={x|(x-2)(x-3)≥0},T={x|x>0},則S∩T=( )
A. [2,3] B.(-∞,2]∪[3,+∞)
C.[3,+∞) D.(0,2]∪[3,+∞)
分析 本題考查解一元二次不等式和集合的運算.解本題的關鍵是解一元二次不等式化簡集合S,再利用數軸進行數形結合,加以直觀的分析和求解.
解 ∵S={x|(x-2)(x-3)≥0}={x|x≤2,或x≥3} ,T={x|x>0},
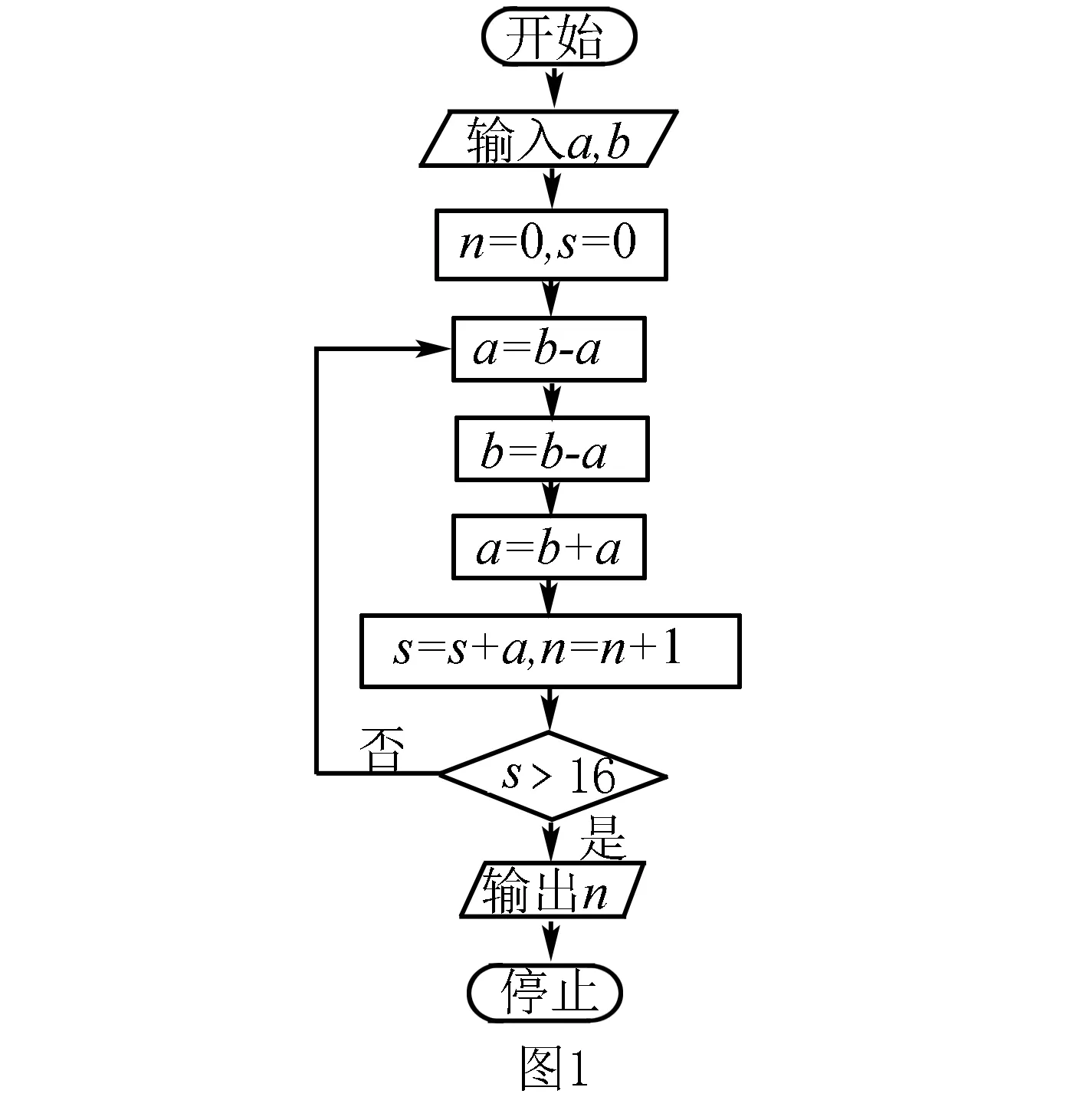
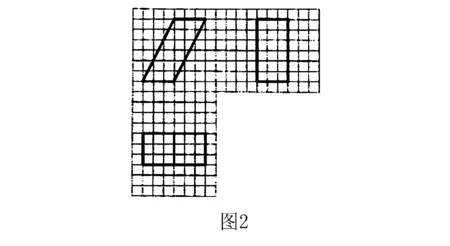
∴S∩T= {x|x≤2,或x≥3}∩{x|x>0}={x|0 點評 一般來說,與集合有關的題型有:集合的基本概念與集合間的基本關系, 集合的運算, 集合中的元素個數,集合的子集個數,與集合有關的參數問題,與集合有關的新概念問題,與集合有關的綜合問題. A.1 B.-1 C.i D.-i 點評 一般來說,與復數有關的題型有:利用復數概念解決點的位置關系,利用復數相等解決復數方程問題,利用復數有關概念及性質解計算問題,利用復數的幾何意義解題,復數與其它知識綜合問題. 例3(2016全國Ⅲ卷,理7)執行如圖1的程序框圖,如果輸入的a=4,b=6,那么輸出的n=( ). A.3 B.4 C.5 D.6 分析 本題主要考查程序框圖條件分支結構和循環結構的理解能力,判斷框中既是算法程序分支執行的條件,同時也決定著循環的次數,一般按流程書寫即可.解答本題的關鍵是對循環結構作用的理解,特別是循環中的計算器作用的理解.本題易將循環次數搞錯. 解 第一次循環后,得b=4,a=6,s=6,n=1; 第二次循環后,得b=6,a=4,s=10,n=2; 第三次循環后,得b=4,a=6,s=16,n=3; 第四次循環后,得b=6,a=4,s=20>16,n=4,輸出結果為4,故選B. 點評 對算法程序框圖和算法語句功能的考查,多以選擇題、填空題的形式出現,出題熱點為程序框圖,難點為條件分支結構和循環結構的理解,易錯點為循環次數.高考命題主要有三種形式,一是給出程序框圖和初始數據,求輸出結果;二是給出框圖與輸出結果,推理輸入的某數據;三是以程序的形式進行考查. 例4 (2016全國Ⅱ卷,理9)如圖2,網格紙上小正方形的邊長為1,粗實線畫出的是某多面體的三視圖,則該多面體的表面積為( ) 分析 做本題的關鍵根據所給的三視圖還原為空間幾何體,由所給的三視圖可知該幾何體是斜四棱柱. 點評 對于給出幾何體的三視圖,求其體積或表面積的題目, 關鍵在于要還原出空間幾何體,并能根據三視圖的有關數據和形狀推斷出空間幾何體的線面關系及相關數據,至于體積或表面積的求解套用對應公式即可;高考命題主要有以下幾種形式:從幾何體到三視圖,從三視圖到幾何體,從三視圖到證明計算. 分析 作出線性約束條件所表示的可行域,然后作出與直線x+y=0平行的直線,通過平行移動,在可行域內求出最大值. G632 B 1008-0333(2017)01-0002-02二、與復數有關的題型
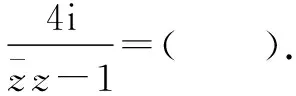
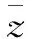
三、與程序框圖有關的題型
四、與三視圖有關的題型
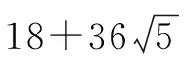
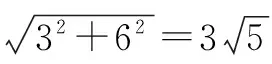
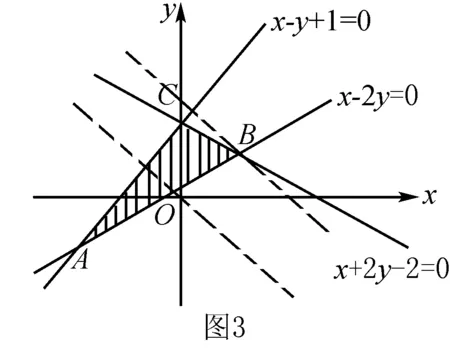
五、與線性規劃有關的題型