含參數不等式恒成立問題的求解技巧

江蘇省淮陰中學高三(6)班(223000)

范 茗●

含參數不等式恒成立問題的求解技巧

江蘇省淮陰中學高三(6)班(223000)

范 茗●

所謂含參數參不等式恒成立問題，主要是指在恒成立條件下，已知不等式解集求參數的取值范圍問題，它涉及知識點多，覆蓋范圍廣，思想方法深刻，技巧性、綜合性以及靈活性強，是歷年數學高考的熱點和難點內容.不少同學在求解含參數不等式恒成立問題時，往往束手無策，難以找到突破口，對此，筆者總結了含參數不等式恒成立問題的幾種求解技巧和方法，以供同學們參考借鑒.

一、參數分離，最值轉化

參數分離，是求含參數不等式恒成立問題較為常用的方法之一，它是指在含有參數的不等式恒成立問題中，借助恒等變形，將所求參數(或其代數式)從不等式中分離出來，并置于不等式一端，從而將原問題轉化函數最值或值域問題，簡化解題過程，使問題快速有效獲解.

例1 已知函數f(x)在R上是減函數，對一切x∈R不等式f(m2-2sinx)≤f(2m+1+cos2x)成立，求實數m的取值范圍.

解 ∵函數f(x)在R上是減函數，由題設不等式知

m2-2sinx≥2m+1+cos2x對一切x∈R恒成立，

∴m2-2m-1≥cos2x+2sinx對一切x∈R恒成立，

設g(x)= cos2x+2sinx，∴m2-2m-1≥[g(x)]max.g(x)= cos2x+2sinx=-sin2x+2sinx+1=-(sinx-1)2+2,

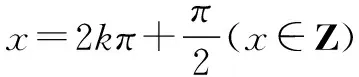
點評 對于某些含參數不等式恒成立問題，可將其中的參數分離出來，轉化為求函數最大值或最小值問題.通常有:①f(x)g(a)(a為參數)恒成立?f(x)min>g(a).

二、分類討論，嚴謹思維

分類討論法，是數學解題中至關重要的思想方法.在解含參不等式恒成立問題時，若參數取值范圍不同，或不等式左右兩邊的函數存在不確定因素時，可通過分類討論的方法對參數進行求解，在分類討論時應注意明確分類標準，做到不重復，不遺漏，從而提高解題的嚴謹性和準確性.

例2 設函數f(x)=x2+bx+c(b、c∈R).若對任意x1,x2∈[-1,1],有[f(x1)-f(x2)]≤4,求b的取值范圍.

解 題設等價于f(x)在[-1,1]上的最大值和最小值之差M≤4，所以：

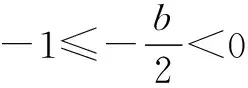
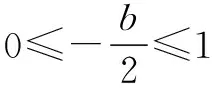
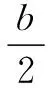
綜上所述，可知b的取值范圍是[-2,2].

點評 對于含參數不等式恒成立問題，倘若無法通過恒等變形分離參數，此時可以借助分類討論的思想進行分析和求解.

三、數形結合，直觀求解

數形結合法，直觀形象.其特點是“見數想形，以形助數”，是求解含參不等式恒成立問題不可或缺的方法之一.在解某些含參不等式恒成立問題時，我們可以先將不等式兩端的式子看成兩個不同的函數，然后分別畫出這兩個函數的圖象，接著觀察函數圖象特征和位置關系，最后列出有關參數的不等式，從而使問題迎刃而解.

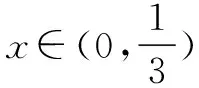
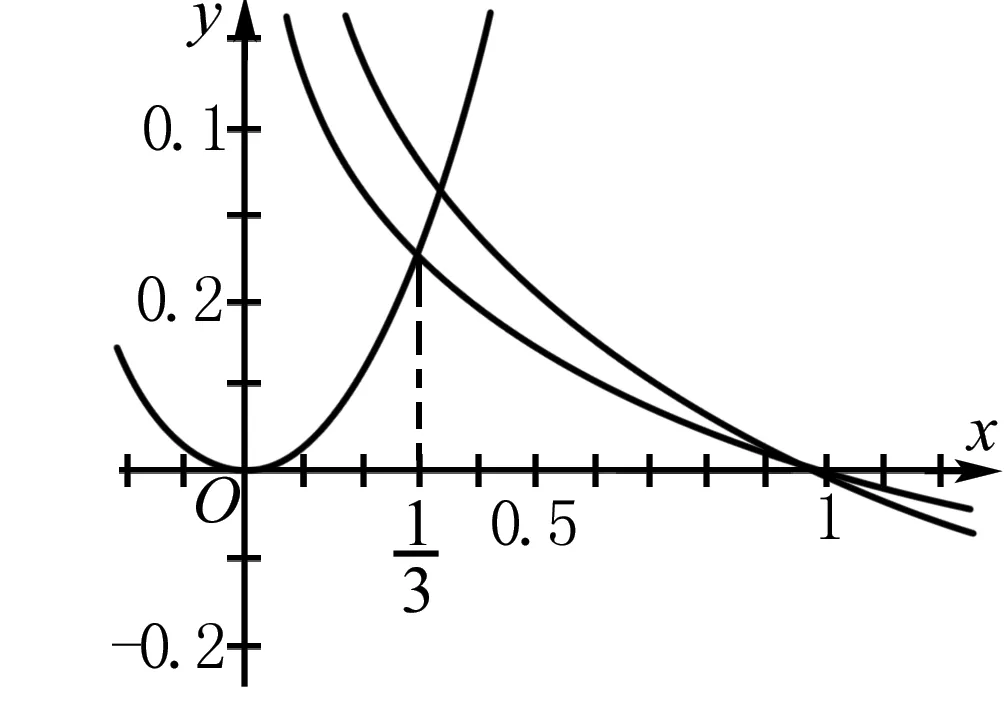
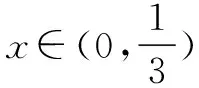
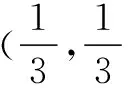
點評 對于一些難以分離參數的不等式恒成立問題，可以利用數形結合思想，先作出符合已知條件的函數圖象或圖形，再利用函數圖象的直觀性，列出不等式，求出參數的取值范圍.

總之，含參數不等式恒成立問題的求解方法靈活多樣，不拘一格.在平時數學解題和學習中，同學們應注意多探索、多思考、多歸納、多總結，不斷積累經驗，掌握技巧和方法，從而提升自己的解題能力，有效突破解題障礙.

指導老師：陳 勇

G632

B

1008-0333(2017)01-0058-01