函數(shù)圖象在高中數(shù)學(xué)解題中的應(yīng)用

湖南省長沙市麓山濱江實驗學(xué)校(410000)

劉佳偉●

函數(shù)圖象在高中數(shù)學(xué)解題中的應(yīng)用

湖南省長沙市麓山濱江實驗學(xué)校(410000)

劉佳偉●

函數(shù)在高中數(shù)學(xué)中占據(jù)著非常重要的地位，函數(shù)的數(shù)形結(jié)合的思想也是高中數(shù)學(xué)學(xué)習(xí)大綱中必須掌握的一個重要思想.函數(shù)圖象在高中函數(shù)學(xué)習(xí)中的運用其實是非常普遍的，其目的主要是提高解題速度和解題的準確性.本文主要就自己的切身經(jīng)驗談?wù)勱P(guān)于函數(shù)圖象在高中數(shù)學(xué)解題中的應(yīng)用的一些看法.

函數(shù)圖象；高中數(shù)學(xué)；函數(shù)學(xué)習(xí)

函數(shù)圖象與數(shù)學(xué)解題之間其實是存在著非常微妙的聯(lián)系，函數(shù)圖象在很多情況下使得數(shù)量關(guān)系和立體的空間得以巧妙地結(jié)合，并且往往我們還能從這種結(jié)合的圖象中思索觀察出題目問題的解決方法.在高中的數(shù)學(xué)學(xué)習(xí)中，實際的解題經(jīng)驗會教會我們，將函數(shù)作為解析的主要過程，往往能夠在很多情況下把較為復(fù)雜難解的問題簡單化.

一、函數(shù)圖象在數(shù)學(xué)選擇題解題中的運用

1.判斷函數(shù)的零點

在判斷函數(shù)的零點以及有幾個零點這類的題目中，函數(shù)圖象往往能夠在解題中起到很大的作用.

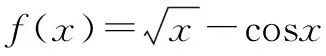
A.沒有零點 B.有且僅有一個零點

C.有且僅有兩個零點 D.有無窮多個零點

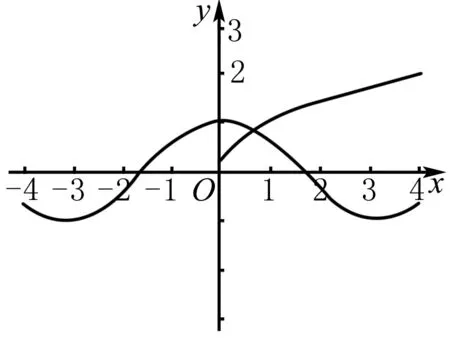
2.在指定區(qū)間內(nèi)判斷方程的根的個數(shù)

例2 方程2x+x3-2=0在區(qū)間(0,1)內(nèi)的實根個數(shù)是( ).

A.0 B.1 C.2 D.3

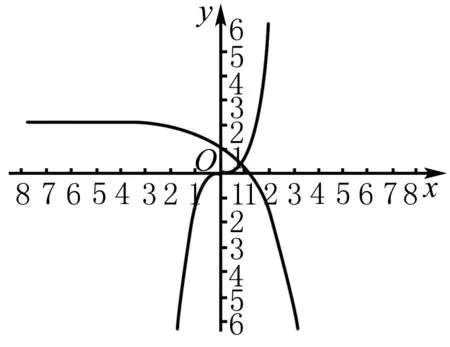
解法 1.將題目中的方程2x+x3-2=0拆分成為兩個函數(shù)f(x)=2-2x,g(x)=x3,這樣再根據(jù)兩個拆分函數(shù)圖象就可以很直觀地根據(jù)它們的交點的個數(shù)來判斷出在區(qū)間(0,1)內(nèi)的零點個數(shù)，如圖，也就是說在區(qū)間(0,1)內(nèi)原函數(shù)的零點個數(shù)只有1個.

3.利用函數(shù)圖象比較大小

例3 若loga2

A．1

C．0

解析 ∵loga2

∵loga2

∴a>b.∴0

二、函數(shù)圖象在含參數(shù)方程中的運用

含參數(shù)方程是指方程的系數(shù)沒有確定，要根據(jù)方程根的分布去判斷參數(shù)的范圍.這樣的題目小題、答題都有，但是一般都會和其它的知識點綜合比如不等式、數(shù)列等.

例4 關(guān)于x的實系數(shù)方程x2-ax+2b=0的一個根在區(qū)間[0,1]上，另一個根在區(qū)間[1,2]上，則2a+3b的最大值為____.

畫出可行域，可求得目標函數(shù)z=2a+3b的最大值是9.

三、利用函數(shù)圖象結(jié)合二分法求方程的近似解

二分法是指利用區(qū)間兩端對應(yīng)的函數(shù)值異號，就可以得知該區(qū)間內(nèi)就必有實數(shù)根，通過計算區(qū)間中點對應(yīng)的函數(shù)值，然后將區(qū)間一分為二，將函數(shù)值為異號的區(qū)間繼續(xù)進行二分，直至達到精準的要求.

例5 求方程lgx=3-x的近似解(精確度0.1).

原方程為x+lgx-3=0，令f(x)=x+lgx-3，可用計算器得f(2)≈-0.70，f(3)≈0.48，于是f(2)f(3)<0，所以這個方程在區(qū)間(2,3)內(nèi)有一個解.用二分法，取區(qū)間(2,3)中點2.5，f(2.5)≈-0.10，再取區(qū)間(2.5,3)的中點，2.75 ，f(2.75)≈0.19，f(2.5)f(2.75)<0，所以x0∈(2.5,2.75).同理可得x0∈(2.5,2.625)，x0∈(2.5625,2.625).由于2.625-2.5625=0.0625< 0.1，所以原方程的近似解可取為2.5625.

其實函數(shù)圖象在高中數(shù)學(xué)解題中的應(yīng)用是非常廣泛的，有時候它能夠很有效地提升我們的解題速度，但是前提是作為學(xué)生，我們必須要掌握各種函數(shù)的基本性質(zhì)，對于函數(shù)的相關(guān)模型有充分的理解，并且在能夠多做相關(guān)的練習(xí)題進行針對性的練習(xí)，平時要多加思考.

[1]李玉蓮.函數(shù)圖象在高中數(shù)學(xué)解題中的應(yīng)用[J].數(shù)理化學(xué)習(xí):高三版, 2015(6):54-54.

[2]鄒麗麗.函數(shù)與方程思想在高中數(shù)學(xué)解題中的應(yīng)用[J].高中數(shù)理化, 2014(22):6-6.

[3]王鵬.淺談數(shù)形結(jié)合思想在有關(guān)高中數(shù)學(xué)解題中的應(yīng)用——以函數(shù)和集合為例[J]. 商情, 2015:254-255.

G632

B

1008-0333(2017)01-0042-01