一道課本習題的高考鏈接

四川省資陽市雁江區伍隍中學(641300)

袁 成●

一道課本習題的高考鏈接

四川省資陽市雁江區伍隍中學(641300)

袁 成●

本文通過對一道線性規劃課本習題的研究，更加深刻地使我們認識到高考題源于課本而高于課本.

高考；線性規劃

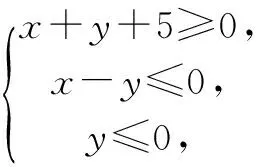
分析 首先作出約束條件表示的平面區域，然后利用平移直線2x+4y=z，使此直線的縱截距取得最小值，則就可求得z的最小值．

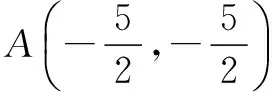
點評 本題主要考查在約束條件下求目標函數的最值．此類試題解答的一般步驟：(1)根據約束條件作出可行域；(2)明確目標函數z與相應直線的截距之間的關系；(3)平移直線確定最優解，并求出最值．

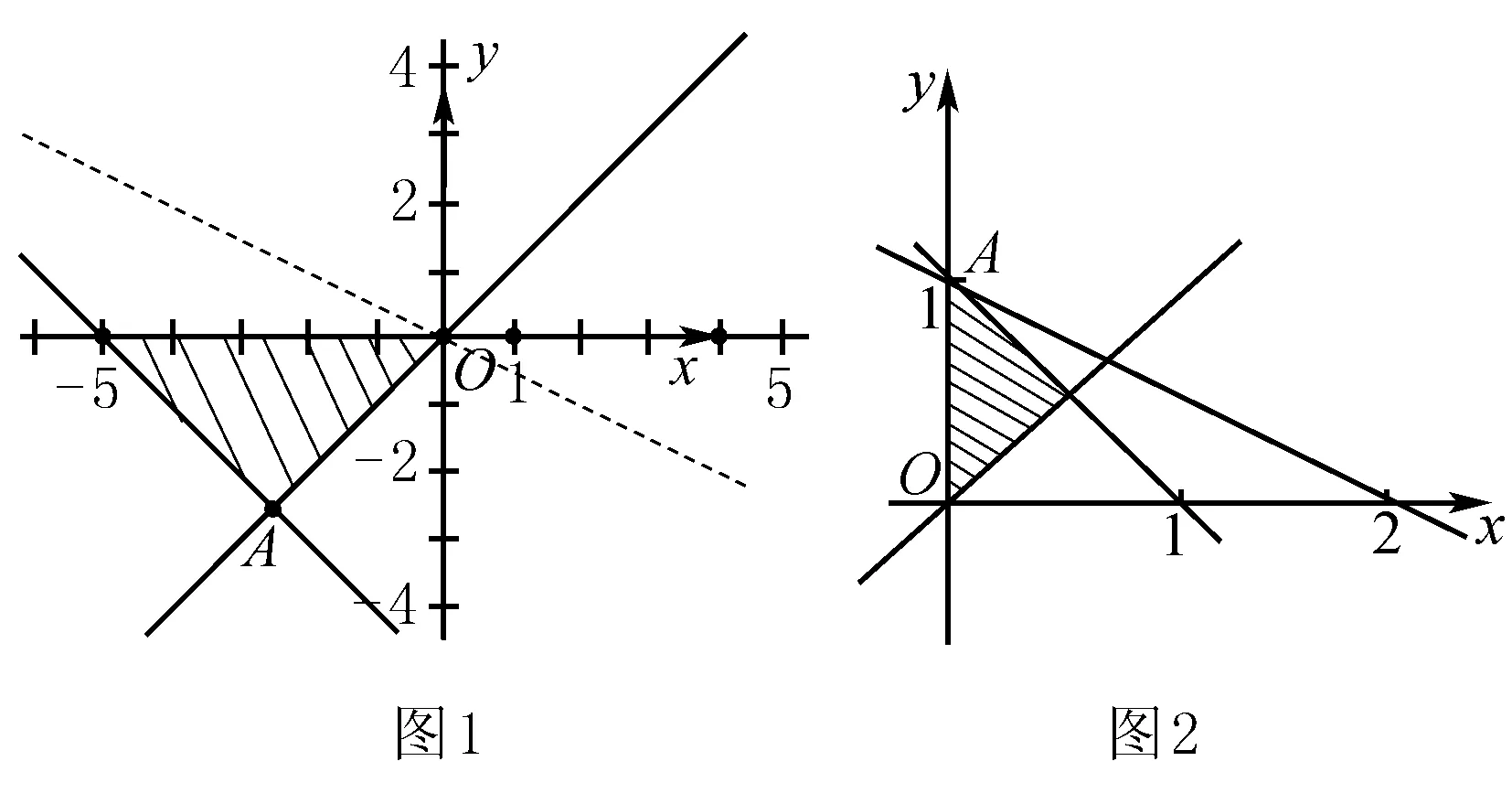
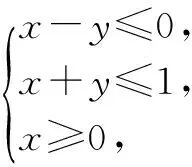
解 如圖2，先畫出可行域.易見直線l:z=x+2y過點A(0，1)時直線的截距最大，z取得最大值2.故選D.

點評 本高考題與課本習題約束條件和目標函數基本一致，變為求目標函數的最大值，但解答思路及過程與課本習題沒有有變化．

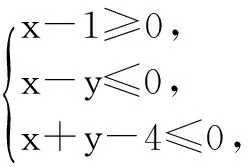
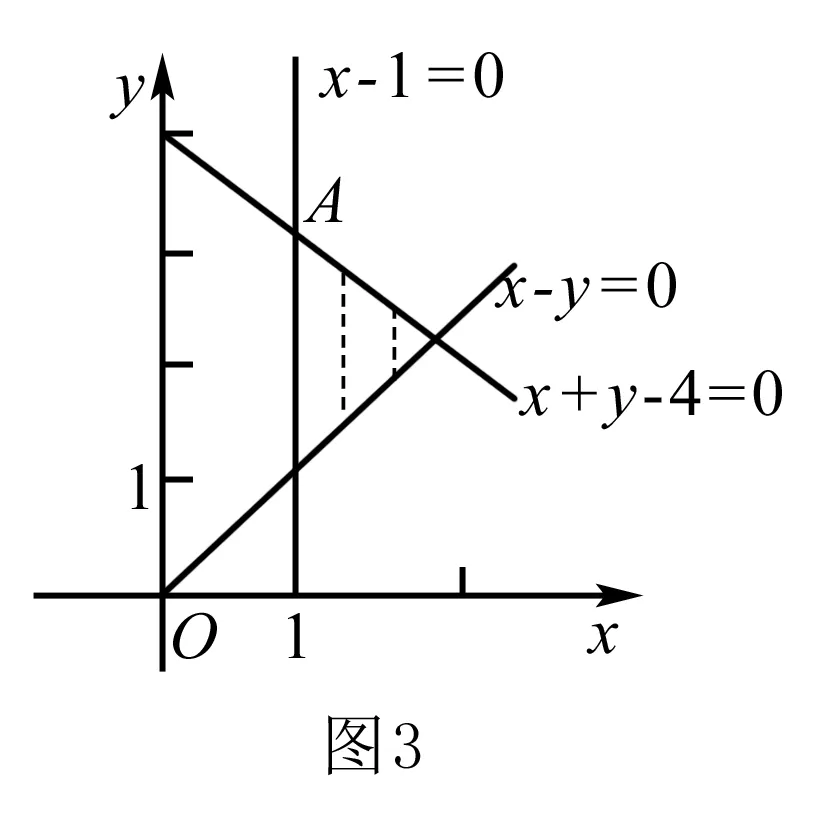
點評 本高考題與課本習題約束條件的給出方式完全一樣，但所解答目標函數在形式上有了一定的變化，即目標函數變為了非線性的問題.

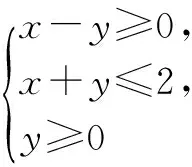
A．3 B．2 C．-2 D．-3

分析 首先作出滿足不等式組的平面區域，根據最優解的值與目標函數對應直線的斜率考慮可能的最優解，進而求a的值．

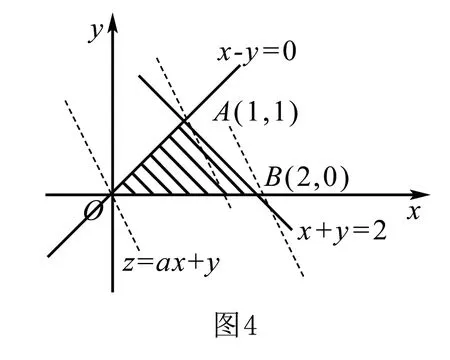
點評 本高考題源于課本卻高于課本，它將原來的正向問題變成了逆向問題，由原來的求目標函數的最值改為已知目標函數最值求參數問題.

[1]嚴士健，王尚志.數學5(必修)[M].北京：北京師范大學出版社，2011.

[2]中華人民共和國教育部制訂.全日制義務教育數學課程標準(實驗稿)[M].北京：北京師范大出版社,2001.

G632

B

1008-0333(2017)01-0059-01