假設法和構造對稱函數解題法在L型函數中的應用

成都市第二十中學校高2017屆08班(610036)

唐芯瑤●

假設法和構造對稱函數解題法在L型函數中的應用

成都市第二十中學校高2017屆08班(610036)

唐芯瑤●

構造對稱函數解題方法是2016新課標全國卷Ⅰ所出現新題型的主要解題方法，也是多數數學學者解決問題的思路方法.本文通過高考的新題型，重點對假設法和構造對稱函數解題法在函數中的應用進行剖析.

構造；對稱；翻折；函數

在高中數學學習的過程中，會運用所學習的有限知識解數學問題是其關鍵內容.當我們使用正確的方法、多種的解題思路，可以使問題很快圓滿的解決；相反，我們使用方法不當，思路單一，就會影響解題的速度和效果.現在對高考出現的一種新題型進行探討，運用假設法和構造對稱函數的方法在來解決函數的取值問題和函數零點之和不等式應用問題.

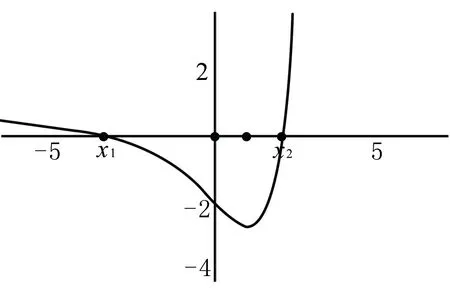
例題 (2016·新課標全國卷Ⅰ)已知函數f(x)=(x-2)ex+a(x-1)2有兩個零點.

(1)求a的取值范圍；

(2)設x1，x2是f(x)的兩個零點，證明：x1+x2<2.

解 (1)求得f′(x)=(x-1)ex+2a),x∈R.

(注：任意題目均不可忽略定義域，否則在某些題目中可能難度出現難度倍增；我們常常所說的求函數——實際是包含了解析式與定義域兩部分)

1°當a>0時：x∈(1,+∞)時，f′(x)>0,f(x)在(1,+∞)上單調遞增；

x∈(-∞,1)時，f′(x)<0,f(x)在(-∞,1)上單調遞減.

∴f(x)min=f(1)=-e.

由零點存在性定理得：a>0時，f(x)在R上必定存在兩個零點，故a>0時成立.

2°當a=0時，f(x)=(x-2)ex,f′(x)=(x-1)e

令f′(x)=0得x=1(故函數單調性同1°)

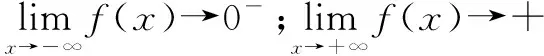
由零點存在性定理得：a=0時，f(x)在R上有且僅有一個零點，故a=0時不成立.

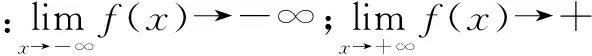
由f′(x)=0得x=1或x=ln(-2a).

由f(1)=-e，而f(x)有兩個零點，只能f(ln(-2a))=0，此方程無解.

綜上所述：a≥0(此類問題用極限法討論較為簡便，相對于標準答案)

(2)由(1)知：

當a≥0時，f(x)有兩個零點x1,x2,不妨令x1<1

x1≥0時，f(x)=(x-2)ex+a(x-1)2;設f(x)關于x=1對稱函數為g(x)=f(2-x)=-ex+a(1-x)2(x≤1).

(注：設構造對稱函數是解題的關鍵，因為這樣我們就可以將一個零點翻折到另一邊作比較.相當于比較原函數在極值點兩側的增長率，實則是左側增長的比右側慢，但是這個問題過于抽象，因此我們構造一個對稱函數來說明，無非就是左側零點關于x=1的對稱點所取得的函數值比右側零點大)

令u(x)=g(x)-f(x),(x≤1)

?u(x)=-ex+a(1-x)2-(x-2)ex-a(x-1)2

?u(x)=(1-x)ex≥0

∴x≤1時，g(x)>f(x),∴g(2-x2)>f(2-x2).

而g(2-x2)=f(x2)=f(x1),

∴f(x1)>f(2-x2),又∵f(x)在(-∞,1)上為單調遞減

∴x1

已知函數f(x)=ex-ax有兩個不同的零點x1,x2,且x2e1x2+x2>2x2x1+x2<2x0(此類題目遇見時應先將參數分離出來然后再單獨翻折函數證明，將參數看作一條平行于x軸的直線與分離的新函數相交證明，往往新函數的極值點是突破題目的關鍵).

評注 觀察2016年課標Ⅰ卷的標準答案，大家可能看的似乎一頭霧水，實則這是一種構造了對稱函數的翻折證明，這類證明問題的通法便是這樣.追求簡易是的數學的魅力所在，而不在于追求難度和復雜度.我們今天應用的假設法和構造對稱函數的方法，正是高考數學用所體現的追求簡易，注重數學基礎，凸現數學的本原.在例題中應用了函數的單調性，假設法，構造函數法，簡易的說我們可以給他一個親切的名字:翻折證明法，學生學習起來也淺顯易懂.

[1]黃加衛.給數學構造性解題方法提個醒[J].中學生數學研究，2006，4：26-28.

[2] 薛金星.怎樣解題[M].北京: 北京少年兒童出版社,2003.

[3] 全日制義務教育數學課程標準[M].北京:北京師范大學出版社,2001.

G632

B

1008-0333(2017)01-0037-01