超大型集裝箱船能效設計指數優化研究

王剛成，馬 寧，顧解忡

(上海交通大學 船舶與海洋建筑工程學院 海洋工程國家重點實驗室高新船舶與深海開發裝備協同創新中心，上海 200240)

超大型集裝箱船能效設計指數優化研究

王剛成，馬 寧，顧解忡

(上海交通大學 船舶與海洋建筑工程學院 海洋工程國家重點實驗室高新船舶與深海開發裝備協同創新中心，上海 200240)

采用船型優化方法就超大型集裝箱船 10 000TEU 的能效設計指數（EEDI）進行優化。文中以降低對主機功率的需求、提高能效設計水平為目標，優化該超大型集裝箱船的阻力性能。優化時利用平移法和徑向基函數方法進行船體曲面重構，并分別采用基于 Rankine 源非線性勢流理論和邊界層動量積分計算興波阻力和摩擦阻力，最后同時使用遺傳算法（NSGA-II）和序列二次規劃算法（NLPQL）在設計空間中探索滿足約束條件的阻力最優船型。結果表明，通過該優化方法獲得的最優船型，其能效設計指數優化程度明顯，能夠滿足現階段 IMO 對新造集裝箱船計及折減系數后的強制要求。

EEDI；船型優化；阻力；折減系數

0 引 言

船舶及航運行業是工業制造及交通運輸中的重要產業，但其能耗及碳排放的增長幅度卻遠超其他行業水平[1]，國際海事組織 IMO 已于 2009 年 MEPC59 次會議上通過了“新船能效設計指數（EEDI）計算方法臨時導則”作為綠色船舶設計的關鍵參考性指標，旨在通過限制船舶 CO2排放來進行船型優化，并促進節能環保船型的開發。另一方面，集裝箱船作為目前三大主流船型之一，所產生的溫室氣體排放量在所有船型中占比最高[2]，其載重噸位也正逐年快速增加，集裝箱船的超大型化已成為近年來的趨勢，然而我國目前有超過 57% 集裝箱船能效設計水平未達到 IMO 規定的EEDI 最低要求[3]，因此提高超大型集裝箱船的能效設計水平為應對全球變暖問題具有十分重要的意義。

EEDI（Energy Efficiency Design Index）是集船舶快速性、耐波性、節能減排技術等于一體的衡量船舶CO2排放量的指標，該指標的制定是為了提高船舶能效和降低二氧化碳的排放。劉飛[4]對 EEDI 公式本身、適用船型、基線公式、折減系數和敏感性因素均做了較為全面的分析；劉亮[5]對關鍵參數失速系數 fw進行了深入研究，采用不同計算方法得到波浪增阻并與實驗值進行比較，為精確計算失速系數提供了參考依據；在此基礎上，封培元等[6]進一步考慮了船機槳之間的匹配問題，提出了一種計算結果較 IMO 推薦方法更為保守的失速系數計算方法；顏林[7]在對國內大量實船進行能效水平評估的基礎上，提出了節能百分比計算公式，并進一步討論了設計航速對 EEDI 的影響；而程紅蓉等[8]則直接利用 Friendship-Framework 船型優化軟件平臺，結合 EEDI，對 1 艘油船進行了主尺度結合型線的多目標優化。

本文針對超大型集裝箱船 10 000TEU，維持其服務航速和推進效率不變，在船舶初步設計階段通過對其型線進行優化、減少航行阻力，以降低該超大型集裝箱船對裝機功率（主機功率）的需求，從而減少燃油消耗、降低 CO2排放量，達到 IMO 對能效設計指數的要求。在對該目標船型優化過程中，利用平移法與徑向基函數方法進行船體曲面重構，采用基于 Rankine 源非線性勢流理論的 SHIPFLOW 軟件計算興波阻力，考慮到優化過程中船型變化對船體表面邊界層的影響，由 SHIPFLOW 邊界層動量積分模塊計算摩擦阻力，以提高總阻力的預報精度，波浪增阻由 Hydro-STAR 計算，最后通過全局優化算法和局部優化算法相結合的方式在設計空間中探索滿足排水量約束條件的最優船型。

1 EEDI 設計指數及基線公式

EEDI（Energy Efficiency Design Index）作為衡量新造船舶 CO2排放量的指標，是當今船舶節能減排領域關注的焦點，最初由巴西在 IMO 環境保護委員會（MEPC）第 58 次會議上提出，其計算公式如下：

其中：

式中各參數的含義文獻[5]中已經有詳細介紹。本文在EEDI 計算過程中，考慮了該超大型集裝箱船在遠東——北美西海岸航線航行時失速系數 fw對 EEDI 的影響（采用 IMO 目前推薦方法），較高精度地估計了該船在該海域航行時 CO2的排放量，表 1 給出了主要參數。

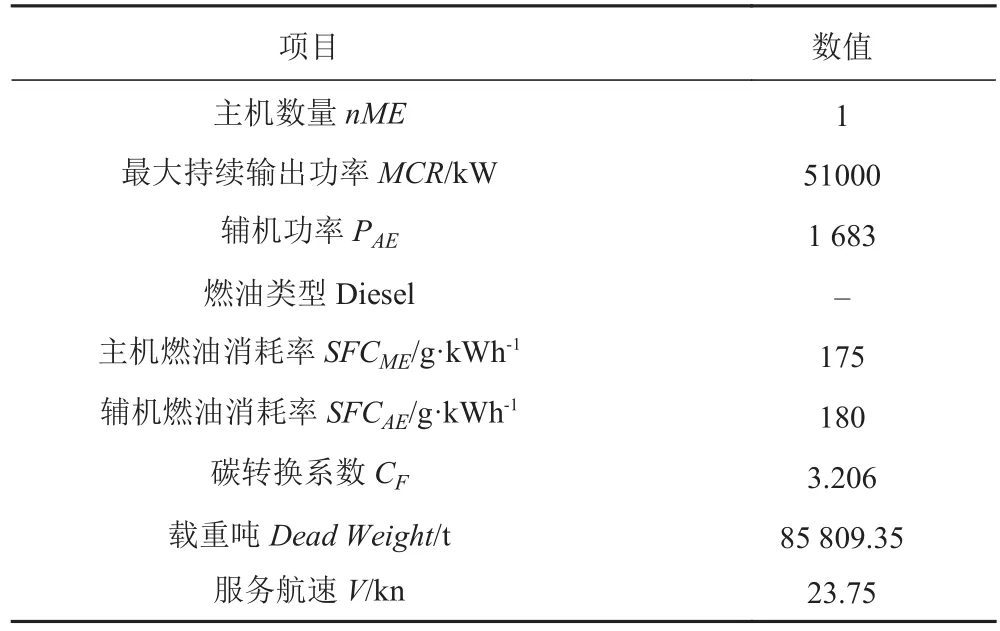
表1 10 000 TEU 集裝箱船能效信息Tab. 1 Energy efficiency information for 10 000 TEU

在提出能效設計指數概念的基礎上，國際海事組織于 2011 年 8 月提出了各船型 EEDI 基線回歸公式，并制定了不同階段相對于該基準線的 EEDI 值的折減率 X，因此新造船舶實際需要滿足的 EEDI 值如下式：

對于集裝箱船，經數據庫統計回歸可得參數 a 和 c的取值分別為 174.22 和 0.201，現階段的折減率 X 為10（施行年限為 2015.1.1–2019.12.31）。因此文中該萬箱集裝箱船的 EEDI 基準值為 17.761 g/t·nm，而目前考慮折減系數后實際需要滿足的 EEDI 規定值為15.985 g/t·nm。

2 船體型線優化

雖然降低主機功率和減小服務航速可以有效控制能效設計水平，但降低航速的方式未綜合考慮船舶實際營運情況，并不適用于所有船型，且通過該方式降低 EEDI 僅能滿足 IMO 設定的基準值，難以達到計及折減系數后的要求[5]。因此本文在維持服務航速和推進效率不變的前提下，以降低對主機功率的需求、減少燃油消耗為出發點，對該超大型集裝箱船的阻力性能進行優化。

2.1 優化目標與算法

通過對船體型線的優化可以有效減小船舶航行阻力從而降低主機功率、減少溫室氣體的排放，以滿足IMO 對新造船舶能效設計指數的要求，本文以超大型集裝箱船 10 000TEU 在服務航速下（Fn = 0.218）的總阻力為目標函數 ，即

式中f 為總阻力系數 Ct。

為了保證優化后船型的合理性，以排水量作為約束條件，優化后的船體排水量（V）與母型船（V0）相差控制在 ± 0.5%以內，即：。

為了找到滿足約束條件下的最優船型，文中首先采用非劣分類遺傳算法 NSGA-II 對整個設計空間進行探索，并以此得到近似全局最優解，然后通過序列二次規劃算法（NLPQL）對其進行反復迭代和更新逐步逼近精確的全局最優解。

2.2 船體曲面重構

本文采用基于整體（平移法）與局部（徑向基函數法）相結合的幾何重構方法對萬箱集裝箱船進行船體表面的幾何變形。

2.2.1 平移法[9]（Shifting Method）橫截面面積曲線（SAC）

目標船型的橫截面面積曲線由如下公式進行表達：

式中：f0(x) 和 fn(x) 分別為變形前后船型的橫截面面積曲線；g(x,α1,α2) 為形狀函數；α1和 α2作為優化過程中的設計變量分別表示橫截面面積曲線的斜率以及平移過程中的固定站位。

2.2.2 徑向基函數插值方法（Radial Basis Function Method）若 x=(xj,yj,zj) 為船體表面離散后的網格節點，

其位移可通過式（8）中插值函數 S(x) 來表達

式中：xj=(xj,yj,zj) 為徑向基函數中心；p 為實現旋轉平移的線性多項式（式 9）；N 為總控制點的個數；? 為對應于歐氏距離 ∥x∥ 的徑向基函數。

選用具有二階連續性的 Wendland[10]方程

則系數 λj、cj可通過聯立插值條件和附加條件（11）來求解線性方程組（12）而獲得

式中：λ=[λ1,λ2,...,λN]T；c=[c1,c2,...,cN]T；f=[f1,f2,...,fN]T。M 和 P 中元素分別為

如圖 1 所示，數字旁邊的黑色控制點表示移動控制點，用于球鼻首和船體進流段處的局部幾何重構；深灰色為固定控制點，用于避免因局部曲率變化過大而變換出較為畸形的中間船型，各優化變量的詳細信息見表 2。

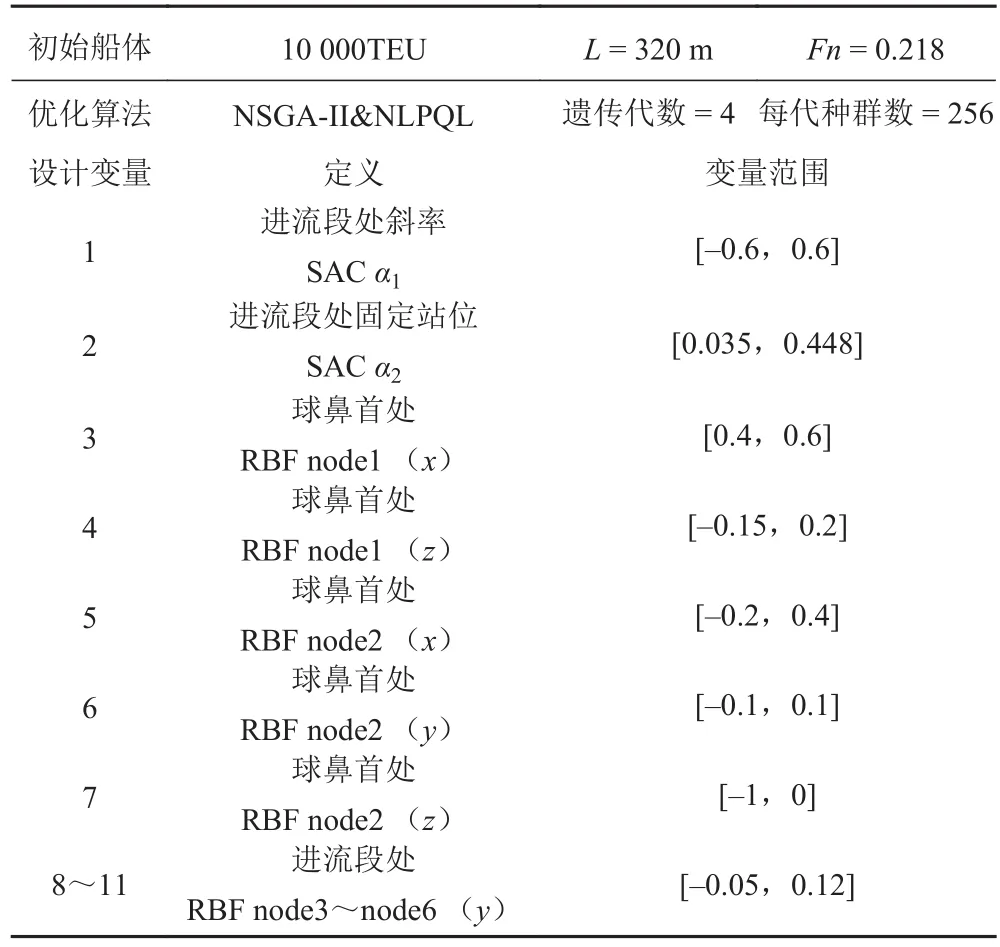
表2 10 000 TEU優化信息Tab. 2 10 000 TEU optimization information

2.3 阻力數值計算方法

船體總阻力由興波阻力和摩擦阻力相加獲得，分別由 Shipflow 軟件的勢流模塊和邊界層動量積分模塊進行計算。該勢流求解器在求解興波阻力時同時采用船體表面壓力積分法和船后波形能量積分法 2 種不同的方法。由于優化過程中船體艏部可能會出現曲率突變或者存在折角的地方、計算網格容易存在缺陷，而采用基于 Rankine 源勢流理論的壓力積分方法計算興波阻力時其結果的穩定性往往對船身網格質量的依賴性較大，實際計算過程中容易出現發散或阻力為負的結果，而采用能量法便可以避免這種情況。另外，由于船體表面壓力的數值積分精度不足等原因[11]，采用能量法計算興波阻力，在精度上也要優于壓力積分法。錢建魁等[12]則通過船模阻力實驗對能量法的阻力預報精度進行了驗證，結果顯示在 Fn?0.29 時 Shipflow 計算值與實驗值吻合良好，因此本文采用 Shipflow 基于 Rankine 源非線性勢流理論的能量積分方法[13]進行興波阻力的求解。文中對超大型集裝箱船進行網格劃分時，船體表面與自由液面分別有 3 857 和 8 240 面元。

3 優化結果與分析

整個優化過程分為 2 步：在第 1 步利用遺傳算法（NSGA-II）全局尋優階段，經過 1 280 次優化后得到了阻力值的全局近似最優解；在此基礎上，采用序列二次規劃法（NLPQL）將上一步得到的近似最優解作為局部尋優的初始設計點，在該點附近運用梯度算法進行優化，直至逼近全局最優解，經過 13 次迭代后計算收斂，優化結束。

3.1 阻力優化結果

表3給出了采用本文船型優化方法后得到的最優船型與母型船關于排水量 ▽、濕表面積 Swet、各阻力系數及總阻力 Rt的數據對比；圖 2 和圖 3 分別為優化前后船型的船體橫剖面圖以及舷側縱切波形圖。

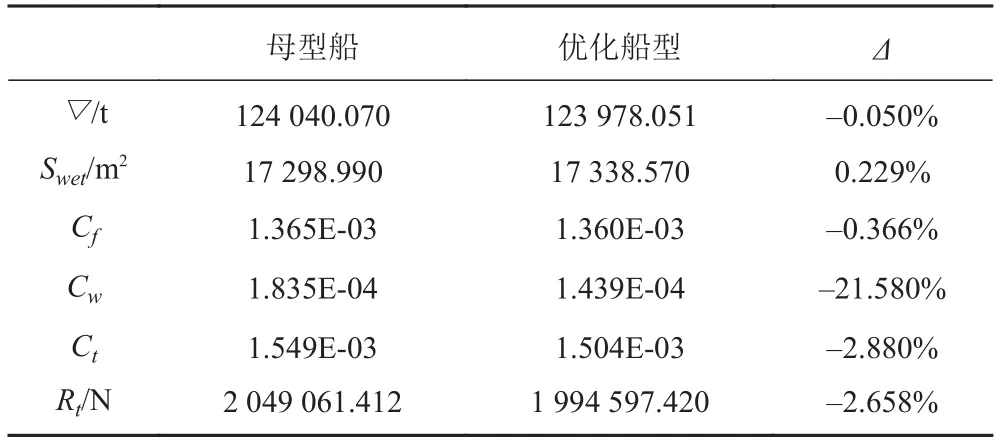
表3 10 000 TEU阻力優化結果Tab. 3 The optimized resistance results of 10 000 TEU

從中可以看出，本文優化后得到的最優船型興波阻力系數較母型船有較為明顯的改善，這一點也可從圖 3 縱切波形圖中各處的峰值均有所減小反映出；盡管波阻系數在總阻力成分中占比較小以及優化后濕表面積有微幅增加，但最終總阻力依然有近 3% 的優化幅度，且排水量和船體型線與母型船相比變化量都十分微弱。

3.2 EEDI 優化結果

圖4 描繪了該超大型集裝箱船所航行的遠東–北美西海岸航線以及該航線所經過的 15 個海區；表 4為優化船型與母型船在不同海區內關于失速系數 fw與能效設計指數 EEDI 的對比；圖 5給出了優化前后的能效設計指數與 IMO 基準值（17.761 g/t·nm）考慮折減系數（X = 10）后的實際規定值（15.985 g/t·nm）的比較。

從中可以看出，經過型線優化后的船型不僅阻力性能有所提高，其在實海域中航行時因波浪增阻（暫不考慮風阻的影響）而造成的失速現象也有所改善；主機所產生的 CO2排放量一般在 EEDI 計算時占主要部分（本文不同海區主機部分占比達到 95% 左右），因此阻力性能優化后的萬箱集裝箱船降低了對主機功 率的需求后，使得優化前其未達到 IMO 對能效設計指數 EEDI 要求的海區（高達 12 個）全部滿足新造船舶計及折減系數后的控制標準，有效減少了溫室氣體的排放。

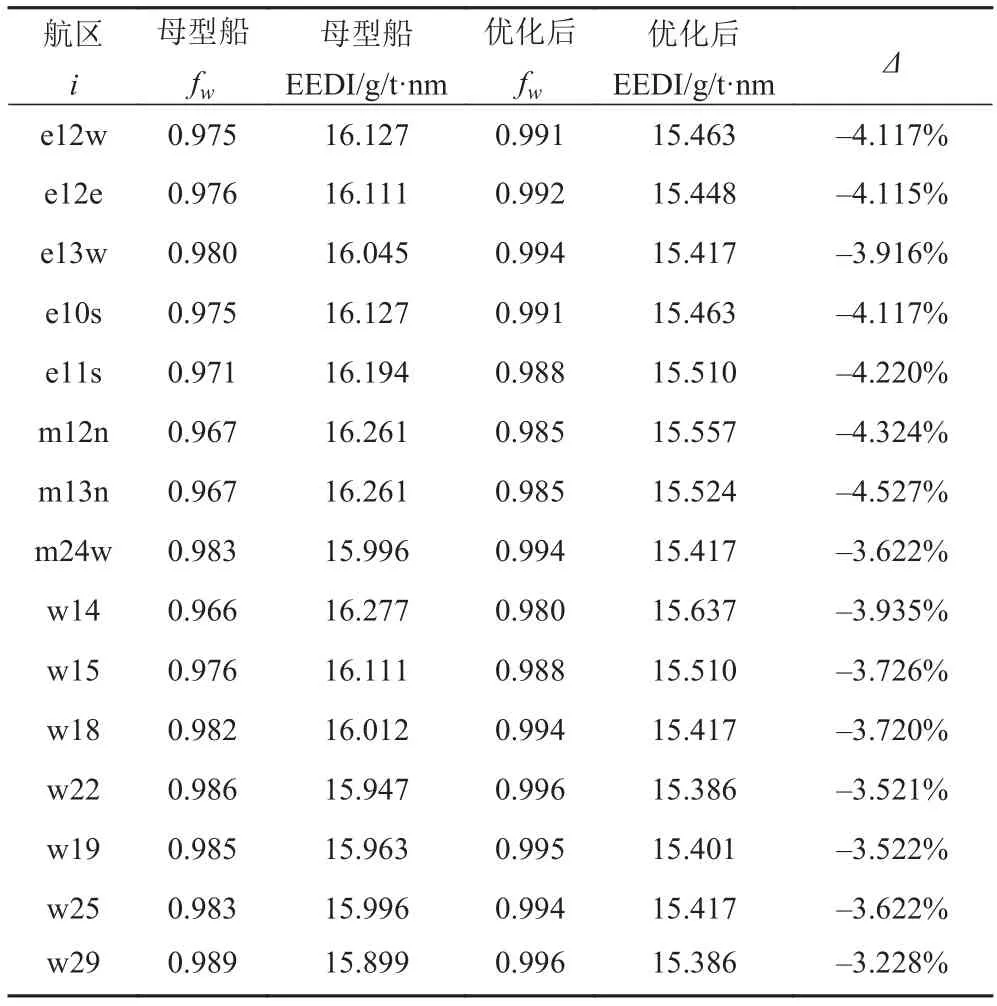
表4 10 000 TEU 遠東–北美航線各海區 EEDI 優化結果Tab. 4 The optimized 10 000 TEU EEDI values in the sea areas of AAN route

4 結 語

本文針對超大型集裝箱船 10 000 TEU，在保持其服務航速和推進效率不變的前提下，以降低對主機功率的需求、減少燃油消耗為出發點，對其船體型線進行了優化。文中同時采用平移法與徑向基函數方法進行船體曲面重構以獲得更多可行的中間船型，并用穩定性更好、計算精度更高的能量積分方法計算興波阻力，最后通過全局尋優與局部優化 2 種算法相結合的方式在設計空間中探索最優船型。最終，通過該船型優化方法獲得的優化船型，其能效設計指數降低程度明顯，能夠滿足現階段 IMO 對新造集裝箱船計及第一階段折減系數后的控制標準，實現了節能減排的目標。

[1]李碧英. 航運業節能減排現狀及其低碳發展的途徑[J]. 工程研究: 跨學科視野中的工程, 2012, 4(3): 260–269. LI Bi-ying. The status quo of energy saving and emission reduction in shipping industry and its approach to low-carbon development [J]. Journal of Engineering Studies, 2012, 4(3): 260–269.

[2]ICCT. The energy efficiency design index (EEDI) for new ships[M]//ICCT. 2011: 1–9.

[3]張云浩. 基于EEDI的集裝箱船技術要素研究[D]. 武漢: 武漢理工大學, 2013.

[4]劉飛. EEDI對船舶總體設計影響分析研究[D]. 大連: 大連理工大學, 2011. LIU Fei. The research of EEDI impact on the basic ship design [D]. Dalian: Dalian University of Technology, 2011.

[5]劉亮. 船舶能效設計中若干耐波性影響因素研究[D]. 哈爾濱: 哈爾濱工程大學, 2010.

[6]封培元, 馬寧, 顧解忡. 基于船機槳匹配和波浪統計的船舶失速系數分析[J]. 上海交通大學學報, 2012(8): 1248-1253. FENG Pei-yuan, MA Ning, GU Xie-chong. Analysis of the ship speed loss coefficient based on hull-engine-propeller matching and wave statistics [J]. Journal of Shanghai Jiao Tong University. 2012(8): 1248-1253.

[7]顏林. 國內船舶能效指數與CO2排放基線實船研究[D]. 武漢: 武漢理工大學, 2011. YAN Lin. Energy efficiency design index and CO2emission baseline based on domestic full-scale ships [D]. Wuhan: Wuhan University of Technology, 2011.

[8]程紅蓉, 劉曉東, 馮佰威. 多目標優化在船型設計中的應用研究[J]. 中國造船, 2014: 76–82. CHENG Hong-rong, LIU Xiao-dong, FENG Bai-wei. Study on multidisciplinary optimization method for hull forms design [J]. Shipbuilding of China, 2014: 76–82.

[9]KIM H. Multi-objective optimization for ship hull form design[D]. George Mason University, 2009.

[10]DE BOER A, VAN DER SCHOOT M S, Bijl H. Mesh deformation based on radial basis function interpolation[J]. Computers & structures, 2007, 85(11): 784–795.

[11]程天柱, 石仲堃. 興波阻力理論及其在船型設計中的應用[M]. 武漢: 華中工學院出版社, 1987.

[12]錢建魁, 毛筱菲, 王孝義. 基于CFD和響應面方法的最小阻力船型自動優化[J]. 船舶力學, 2012, 16(1): 36–43. QIAN Jian-kui, MAO Xiao-Fei, WANG Xiao-yi. Ship hull automated optimization of minimum resistance via CFD and RSM technique [J]. Journal of Ship Mechanics, 2012, 16(1): 36–43.

[13]TELSTE J G, REED A M. Calculation of transom stern flows[C]//Proceedings of the Sixth International Conference on Numerical Ship Hydrodynamics, 1994: 78–92.

Research on the energy efficiency design index optimization of ultra large container ship

WANG Gang-cheng, MA Ning, GU Xie-chong
(State Key Laboratory of Ocean Engineering, Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiaotong University, Shanghai 200240, China)

The Energy Efficiency Design Index (EEDI) of the 10000TEU Ultra Large Container Ship is reduced by ship hull-form optimization method. The drag of the ULCS at design speed is optimized in order to lower the demand for main engine power and improve the energy efficiency design level. During the process of resistance optimization, radial basis function and shifting methods are utilized to modify the hull surface; the calm-water drag is evaluated by the sum of the wave drag predicted by Rankine source method and the friction drag given by boundary layer momentum integral method. Finally, the optimum hull form is obtained via using genetic algorithm (NSGA-II) and sequential quadratic programming (NLPQL) simultaneously. Results show that the EEDI of the optimal hull form obtained by the above optimization approach can be reduced considerably and meet the required EEDI value considering the reduction factor.

EEDI；hull-form optimization；drag；reduction factor

U661.3

A

1672–7619(2017)05–0060–05

10.3404/j.issn.1672–7619.2017.05.012

2016–09–12；

2016–11–04

教育部重大專項資助項目(GKZY010004)

王剛成(1991–)，男，碩士研究生，主要研究方向為綠色智能船舶技術。