基于對極幾何學的紅外目標姿態估計
張喜濤 王暉 張學峰
摘要:通過紅外導引頭獲得目標不同姿態的圖像序列。利用數字圖像分析技術提取序列圖像的匹配點。采用對極幾何學方法求解匹配點之間的變換關系,并解算出目標三維空間信息,進而求得目標姿態信息。本方法徹底擺脫了目標表面控制點要求,簡單、可靠地實現了對紅外非合作目標相對姿態的估計。
關鍵詞:對極幾何學;匹配;紅外目標;姿態估計
中圖分類號:TJ760.3+31;TP391.41 文獻標識碼:A 文章編號:1673-5048(2017)02-0028-05
0引言
按照測量系統與被測目標的關系,可以將姿態測量技術分為合作式和非合作式兩大類。合作式測量方法通過安裝人工標記、獲取目標圖像庫或三維模型、與目標通信等方法進行,該方法的特點是算法簡單、技術成熟、可靠性高,但應用范圍受限。非合作式測量方法則沒有來自目標的主動幫助信息,其常用的測量手段包括導航衛星測量、微波雷達測量、激光成像測量、光學成像測量和組合測量等,其中光學成像測量具有成本低、技術成熟、設備簡單、功耗低、體積小等優點。
隨著計算機視覺理論和技術的發展,相關成果被引入到非合作目標測量方法中,加拿大Andersson等人在NFAS視覺系統中利用雙探測器重建技術取代目標的三維模型,利用模型匹配技術實現非合作目標的姿態測量,其缺陷是雙探測器受限于平臺尺寸、基線較短、工作距離較近。基于圖像特征匹配的方法,通過處理圖像序列得到目標的相對姿態信息,克服了基于模型匹配方法平臺限制的問題,但該方法目前處于理論研究階段,國內外未見基于紅外導引頭平臺的飛機姿態測量文獻。
紅外非合作目標姿態測量技術對近距目標跟蹤和目標要害部位打擊具有重要意義。本文提出的基于對極幾何學的紅外目標相對姿態測量算法,僅利用不同時刻觀測到的紅外視頻圖像,便捷實現了對非合作目標相對姿態的測量,且對平臺沒有過多的限制,有很好的應用前景。
姿態測量系統的總體流程為信息處理器接收到成像系統輸出的圖像后,在目標輪廓范圍內進行圖像匹配,根據目標像素數的不同采用不同的匹配算法,從圖像中找出目標的匹配點坐標,利用匹配點坐標計算目標俯仰和偏航方向角度變化。
1匹配算法
按照目標像素的個數選擇合適的匹配算法,目標像素數大于500時采用SIFT算法;當像素數小于500時,SIFT匹配算法失效,需要按照像素比對的方法進行匹配;當像素數大于50 000時,SIFT算法耗時比較長,對目標輪廓內圖像進行上采樣,可以縮短算法運行時間。
1.1SIFT算法
SIFT算法利用局部特征提取一系列穩定的特征點,進一步利用特征描述向量實現特征點間的匹配。SIFF算法通常可以分為以下步驟:首先,進行尺度空間的構造,形成圖像尺度空間;然后,利用局部極值點檢測算法,提取穩定特征點;其次,對提取的特征點進行特征描述,形成特征向量;最后,采用匹配算法實現特征向量的匹配。
1.1.1尺度空間的構造
尺度空間的構造利用不同尺度的高斯差分核(DOG)與原始圖像進行卷積,形成不同的尺度空間。SIFT算法利用金字塔構建的形式,分別向上向下采樣,形成一種多級多層的差分高斯圖像結構,相鄰兩層的高斯卷積圖像差分得到該尺度下的高斯差分圖像。高斯差分圖像金字塔的級數和層數通常為6和7。SIFT的尺度空間結構如圖1所示。
1.1.2局部極值點檢測
遍歷高斯差分尺度空間,查找與相同尺度周圍點及上下尺度周圍點有明顯區別的局部點作為高斯差分尺度空間的極值點(最大值或最小值)。仿真發現,由于圖像邊緣和對比度較低的極值點通常不夠穩定,應該予以濾除。
1.1.3特征點的描述
在局部極值點周圍取固定大小的窗口,計算窗內各像素與窗口中心點的梯度值和梯度方向。為了使描述子具有旋轉不變性,各像素的梯度方向相對特征點主方向進行旋轉。
1.1.4特征點的匹配
利用特征描述向量的歐式距離判斷特征點的相似程度。如果特征點的最小歐氏距離與次小歐氏距離之比小于0.8,認為該特征點具有穩定的匹配點,描述子具有最小歐氏距離的兩個特征點匹配。
1.2像素比對法
通常,在目標像素數少于500時,用SIFT算法很難得到8個以上的匹配結果。因此必須增加特征點數量以提高匹配點數,這必將增加匹配的錯誤率。將像素灰度大于閾值的點作為特征點,采用5×5的窗口建立與中心點的梯度方向,將25個梯度方向作為特征向量,參照SIFT算法基于特征向量進行匹配。
2匹配點檢測
兩幅從不同視點拍攝的同一場景的圖像中,各對應像素點之間滿足一種約束關系,稱為對極幾何關系,這種約束關系可以用基本矩陣來描述。
2.1基本矩陣
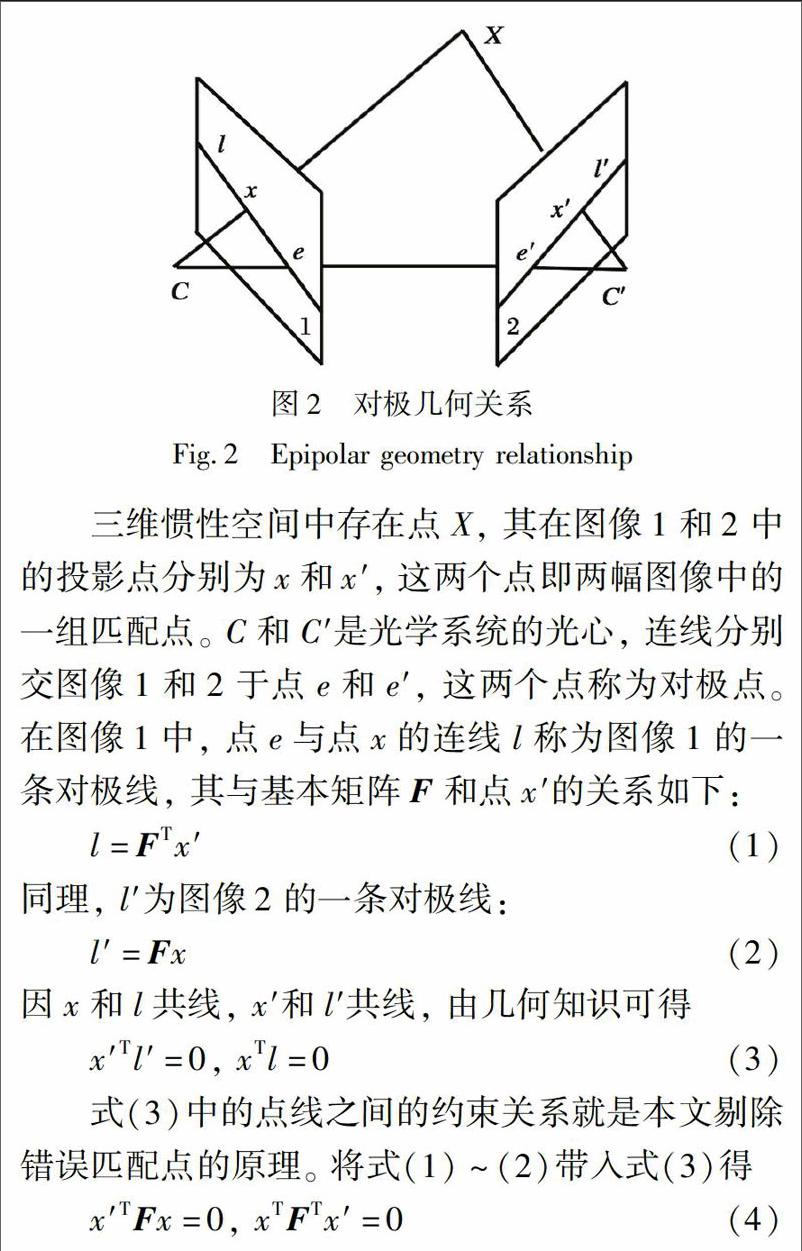
對極幾何關系如圖2所示。
三維慣性空間中存在點X,其在圖像1和2中的投影點分別為x和x,這兩個點即兩幅圖像中的一組匹配點。c和C是光學系統的光心,連線分別交圖像1和2于點e和e,這兩個點稱為對極點。在圖像1中,點e與點x的連線l稱為圖像1的一條對極線,其與基本矩陣F和點x的關系如下:
l=FTx (1)同理,l為圖像2的一條對極線:
l=Fx (2)因x和l共線,x和l共線,由幾何知識可得
xTl=0,xTl=0 (3)
式(3)中的點線之間的約束關系就是本文剔除錯誤匹配點的原理。將式(1)~(2)帶入式(3)得
x'TFx=0,xFTx=0 (4)
基本矩陣F是3×3、秩為2的矩陣,具有7個自由度,由式(4)可知,F矩陣可以由兩幅圖像的8個匹配點解方程組求得。
2.2RANSAC
不同的參數設置下,SIFT算法獲取的匹配點有一定的差異性,通常都包含許多錯誤匹配點,精確合適的匹配點能夠提高F矩陣的求解精度。本文利用對極線幾何約束原理,采用RANSAC擬合的方法,迭代求解最佳F矩陣,同時,獲取精確合適的匹配點。
RANSAC是一種基于隨機采樣序列的估計方法,從一組包含多數正確點和少數錯誤點的數據集合中估計一個最佳的數學模型以獲得正確點,最早由Fischler和Bolles提出。用RANSAC剔除SIFT錯誤匹配點的方法如下:
(1)隨機假設8個SIFT匹配點作為正確的匹配點計算F矩陣,利用求解的F矩陣獲取所有匹配點與其對應的對極線之間的距離,該距離小于一定的門限值的匹配點被認為是正確的,記錄正確匹配點以及F矩陣:
(2)重復步驟(1)N次;
(3)得到正確匹配點數目最多的F矩陣作為最佳的F矩陣。
3姿態測量
單幅圖像的對極幾何關系如圖3所示。圖中,空間點X投影到圖像上的點為x,點C為探測器的光心。令矩陣P為該幅圖像的投影矩陣,P+=PT(PPT)-是矩陣P的逆矩陣。因為點P+x滿足式x=PX,因而點Px和點C都在空間點X的投影線上。
由圖2可知,點C在圖像2上的投影點為e,令P為圖像2的投影矩陣,可得
e=P'C (5)
點P+x在圖像2上的投影在對極線l上,可得
l=(P'C)×(p'p+x)=[e]×(p'p+)x (6)
由式(2)可得
F=[e]×(p'p+) (7)
假設慣性坐標的中心在圖像1的中心,K為探測器內參數矩陣,那么兩幅圖像的投影矩陣分別為
P=K[I|10],P=K[R|t] (8)
可得
(9)
將其代入式(7)可得
(10)
令E=[t]×R,矩陣E稱為關鍵矩陣,與基本矩陣F的關系如下:
E=K'TFK (11)
由式E=[t]×R可知,關鍵矩陣與導引頭的姿態及位置信息有關,經過分解可以得到旋轉矩陣R和平移矩陣t。
大量的實驗研究發現,關鍵矩陣的特征值有兩個相等,另外一個為零。因而關鍵矩陣經過SVD分解可得
E=Udiag(1 1 0)VT (12)由于ETt=0,求解得
t=±U(0
0
1)T=±u3 (13)
4探測器標定算法
在有條件的情況下,進行高精度離線標定,或者利用在線標定技術對探測器內參數進行標定。
離線標定是指利用大型標定板空間點和成像點之間的約束進行標定。考慮到畸變影響,算法采用線性標定和非線性標定結合的二步法。標定,并采用最小二乘法對結果進行優化。
在線標定是指利用SIFT匹配算法得到的匹配點和導引頭的焦距參數作為初值,并利用最小二乘法進行優化。
5仿真及分析
采用3dmax建立探測器模型,探測器模型的鏡頭焦距為0.1 m,分辨率為512×512,探測器在仿真過程中模擬彈目接近過程,彈目距離由1 km接近到200 m。采用Creator軟件建立飛機模型,其長、寬、高分別為21.94 m,14.70 m,5.93 m,見圖4。
對探測器模型進行離線標定,求得該探測器模型的內參數矩陣為
(14)
序列圖像中的兩幅圖像(垂直于紙面向內旋轉了5。)分別采用SIFT算法和RANSAC算法進行匹配點篩選后的結果,如圖5所示。匹配結果準確,說明求解的基本矩陣能夠反映目標的變化。
將飛機模型俯仰角旋轉一定角度,探測器與目標距離由1 km緩慢變近,利用算法求解,試驗結果如表1所示。將飛機模型偏航角旋轉一定角度,探測器與目標距離由1 km緩慢變近,利用算法求解,試驗結果如表2所示。
比較兩組試驗結果,如圖6所示,可以看出兩組試驗結果角度估計誤差隨著彈目距離的接近而減小,且誤差均小于147 mrad,說明該算法能夠為導彈提供目標末端跟蹤和精確打擊所需要的相對姿態信息。
6結論
本文針對利用紅外圖像估計飛機類目標姿態問題,首先利用SIFT算法提取序列圖像的匹配點,然后利用RANSAC算法對匹配點進行校正,最后利用匹配點的對極幾何關系求解飛機的姿態變化角度。試驗結果表明,角度測量的總體誤差較小,隨著距離的減小,匹配對數目增多,角度測量精度隨之提高,說明了算法對紅外目標姿態測量的有效性。
同時,算法也有不足的地方:
(1)算法依賴于匹配點的數目,因此,該算法對紅外圖像質量要求較高;
(2)SIFT算法對系統資源消耗較大,目前僅能從理論上驗證姿態測量算法的可行性,就目前的硬件水平而言,暫無法滿足導引頭實時性要求。