淺談函數“恒成立問題”與“最值問題”的等價轉化
福建省連城一中 張濤生
縱觀近10年全國卷高考數學壓軸題,基本體現以下三個方面的基本關系。
(一)各類不等式與函數最值的關系,如下表。
不等式類型 與最值的關系

?
(二)函數f(x)對區間D的x1、x2,都有恒成立,
3、已知f(x)對總存在對于使得設f(x)在區間D1上的值域為A,g(x)在D2上的值域為B,則A?B.
主要有以下三方面的題型。
一、與三角形構建有關的“恒成立問題”
例1,已知若 在區間[0,2]上任取三個數a、b、c,均存在著f(a)、f(b)、f(c)為邊長的三角形,求實數m的取值范圍。
解:
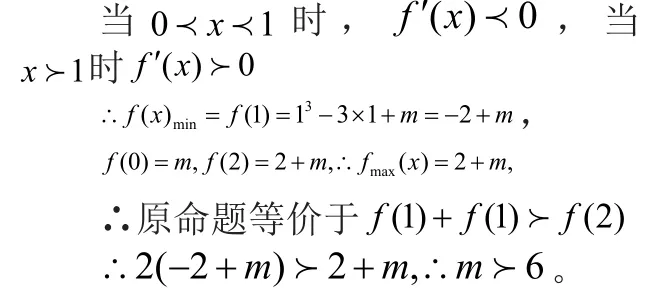
[命題意圖]:把“三角形存在性問題”轉化任意的兩邊之和大于第三邊,轉化為兩條最小邊之和大于最大邊。
二、與不等式有關的“恒成立問題”
例2,已知函數(x)+g(x).若關于x的不等式F(x)≤mx-1恒成立,求整數m的最小值;
解:令
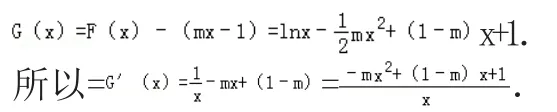
當m≤0時,因為x>0,所以G′(x)>0所以G(x)在(0,+∞)上是遞增函數,
又因為G
所以關于x的不等式G(x)≤mx-1不能恒成立.
當m>0時.
令G′所以當時,G′(x)>0;當時,G′(x)<0.
因此函數G(x)在是增函數,在是減函數.
故函數G(x)最大值為.
令h (m)=因為h(1)h(2)
又因為h(m)在m∈(0,+∞)上是減函數,所以當m≥2時,h(m)<0.
所以整數m的最小值為2.
[解題思路]:利用計算函數在區間D的最大值和最小值解決函數的恒成立問題。
例3,如果函數滿足對任意的都有恒成立,則實數a的取值范圍是?
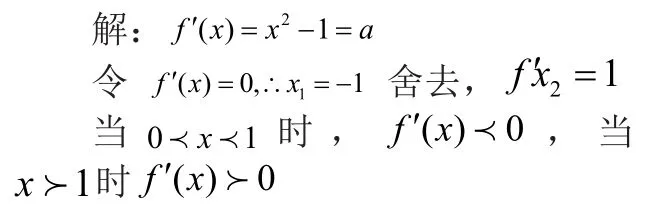

三、與等式有關的“恒成立問題”
例4,已知
(Ⅰ)求的單調區間;
(Ⅱ)若對任意的總存在使求實數a的取值范圍.
解:設在區間[1,e]上f(x)的值域為A,在[0,3]上g(x)的值域為B,
則依題意A?B易知g(x)在[0,1]上遞增,在[1,3]上遞減,
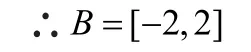
①當a≤0時,f(x)在[1,e]上單調遞增,
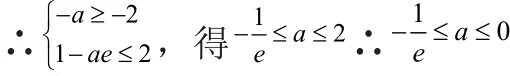
②當a≥1時,f(x)在[1,e]上單調遞減,A = [1 - ae,- a]
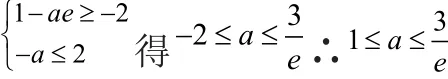
③當時,f(x)在[1,e]上單調遞增,可得
④當時,f(x)在[1,e]上
綜上,實數a的取值范圍為
以上這些例題中,本質問題就是構造函數,把問題轉化為函數的最大(小)值,進而研究函數在區間D上的最值,通過求導,得出極值點的坐標,從而得出函數的最大(小)值,確定參數的取值范圍,這是這類問題的基本解題思想。

