聚焦圓錐曲線的新穎題型

■陜西洋縣中學(xué) 何記英 劉大鳴(特級教師)

聚焦圓錐曲線的新穎題型

■陜西洋縣中學(xué) 何記英 劉大鳴(特級教師)

圓錐曲線的新穎題型主要有：定義的巧用,離心率的求解,焦點(diǎn)三角形的面積,焦點(diǎn)弦長問題,軌跡方程的探究,直線與圓錐曲線的位置關(guān)系,以及證明定值、求定點(diǎn)和相關(guān)最值等。求解時常用到設(shè)而不解、整體思維,有時還要用到平面幾何的基本知識和向量的基本方法。

聚焦一 用圓錐曲線定義探求幾何量

例1 (2 0 1 6年吉林省實(shí)驗(yàn)中學(xué)高三質(zhì)檢)如圖1,過雙曲線的左焦點(diǎn)F1,作圓x2+ y2=a2的切線交雙曲線右支于點(diǎn)P,切點(diǎn)為T, P F1的中點(diǎn)M在第一象限,則以下結(jié)論正確的是( )。

A.b-a=|MO|-|MT|

B.b-a＞|MO|-|MT|

C.b-a＜|MO|-|MT|

D.b-a=|MO|+|MT|

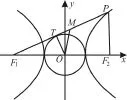
圖1

解析：因?yàn)門為切點(diǎn),則O T⊥P F1。在R t△O T F1中,|T F1|=b,連接P F2,由三角形中位線定理可得+b=b-a。選A。

點(diǎn)評：解決本題的關(guān)鍵是用O T⊥P F1和幾何量的關(guān)系求出|T F1|=b。由中位線定理得,再結(jié)合雙曲線的定義最終求出答案。

聚焦二 構(gòu)建不等關(guān)系求圓錐曲線離心率的取值范圍

例2 (浙江省寧波市效實(shí)中學(xué)2 0 1 6年上學(xué)期期中測試)已知F1、F2分別為的左、右焦點(diǎn),P為雙曲線右支上任一點(diǎn),若的最小值為8a,則該雙曲線的離心率的取值范圍是。

解析：借助雙曲線的定義,再降元,以及運(yùn)用基本不等式解題。欲取到最小值8a,則|P F2|=2a,而|P F2|≥c-a,即2a≥c-a,所以1＜e≤3。

點(diǎn)評：求離心率的值或取值范圍,常依據(jù)題設(shè)條件構(gòu)造a、c的齊二次式,以及借助基本不等式、平面幾何性質(zhì)和曲線本身范圍構(gòu)建a、c的不等關(guān)系式,本題中構(gòu)建a、c滿足的不等關(guān)系時既用到基本不等式取等號的條件,又用到了雙曲線上任一點(diǎn)到其對應(yīng)焦點(diǎn)的距離不小于c-a的幾何性質(zhì)。

聚焦三 焦點(diǎn)三角形面積問題

例3 (四川省綿陽市南山中學(xué)2 0 1 6學(xué)年上學(xué)期期中測試)雙曲線(n＞1)的兩焦點(diǎn)為F1、F2,點(diǎn)P在雙曲線上,且滿足|P F1|+|P F2|=2,則△P F1F2的面積為( )。

解析：假設(shè)點(diǎn)P在右支上,由雙曲線定義可知|P F1|-|P F2|=2。

又因?yàn)閨P F1|+|P F2|=2n+2,所以|P F1|=n+2+n,|P F2|=n+2-n。

因?yàn)閨F1F2|=2n+1,所以|P F1|2+ |P F2|2=|F1F2|2,△P F1F2的面積=1,故選A。

點(diǎn)評：求雙曲線或橢圓的焦點(diǎn)三角形面積,主要用到余弦定理和雙曲線或橢圓的定義以及面積公式這些知識點(diǎn)。若點(diǎn)P為橢圓上非頂點(diǎn)的任一點(diǎn),(a＞b＞0)的兩焦點(diǎn),則=∠F1P F2。對于雙曲線其中θ=∠F1P F2。

聚焦四 與拋物線焦點(diǎn)弦長有關(guān)的問題

例4 (2 0 1 6年遼寧省五校高三上學(xué)期聯(lián)考)如圖2,設(shè)拋物線y2=4x的焦點(diǎn)為F,直線l過F且與C交于A、B兩點(diǎn)。若|A F|=3|B F|,則直線l的斜率為。

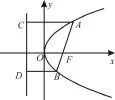
圖2

點(diǎn)評：已知拋物線y2=2p x(p＞0),過其焦點(diǎn)的直線交拋物線于A、B兩點(diǎn)(如圖2所示),設(shè)A(x1,y1),B(x2,y2),用方程研究有以下結(jié)論：

(1)|A B|=x1+x2+p。

(2)x1x2=

(3)以A B為直徑的圓與拋物線的準(zhǔn)線相切。

(4)拋物線的通徑長為2p,是過焦點(diǎn)的弦長的最小值。

(5)以A F或B F為直徑作圓,則此圓與y軸相切。

聚焦五 代入法求動點(diǎn)的軌跡方程

例5 (2 0 1 6年江蘇省南京市模擬卷)如圖3,P是橢圓=1上的任意一點(diǎn),F1、F2是它的兩個焦點(diǎn),O為坐標(biāo)原點(diǎn)

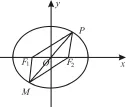
圖3

則動點(diǎn)Q的軌跡方程是。

點(diǎn)評：如果動點(diǎn)Q(x,y)依賴于另一動點(diǎn)P(x0,y0)(即相關(guān)點(diǎn)),而點(diǎn)P(x0,y0)又在某一已知曲線上運(yùn)動,則可根據(jù)向量關(guān)系、坐標(biāo)關(guān)系列出關(guān)于x0,y0,x,y的方程組,利用x,y表示出x0,y0,再把x0,y0代入已知曲線方程,便可得出動點(diǎn)Q(x,y)的軌跡方程。這種方法是代入法。

聚焦六 定義法探究立體幾何和解析幾何交匯的軌跡方程

例6 如圖4,正方體A B C D-A1B1C1D1的棱長為1,點(diǎn)Μ在棱Α B上,且,點(diǎn)P是平面A B C D上的動點(diǎn),且動點(diǎn)P到直線A1D1的距離與點(diǎn)Ρ到點(diǎn)Μ的距離的平方差為1,則動點(diǎn)Ρ的軌跡是( )。

A.圓 B.拋物線

C.雙曲線 D.直線

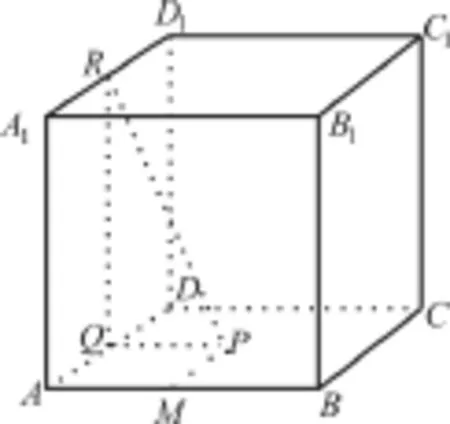
圖4

解析：如圖4所示,過點(diǎn)P作P Q⊥A D,垂足為Q,則P Q⊥平面A DD1A1。過點(diǎn)Q作Q R⊥A1D1,垂足為R,則A1D1⊥平面P Q R,故P R⊥A1D1。

P R即為點(diǎn)Ρ到直線A1D1的距離,則P R2-P Q2=R Q2=1。又已知P R2-PM2=1,故P Q=PM。由拋物線的定義可知動點(diǎn)Ρ的軌跡是拋物線。

點(diǎn)評：求解立體幾何和平面幾何交匯的動點(diǎn)軌跡問題,關(guān)鍵在于利用空間概念合理轉(zhuǎn)換為平面內(nèi)圓錐曲線的定義。為了得到P Q=PM,將已知條件中“動點(diǎn)Ρ到直線Α1D1的距離與點(diǎn)Ρ到點(diǎn)Μ的距離的平方差為1”用數(shù)學(xué)語言表達(dá),即作出點(diǎn)P到線和面的距離進(jìn)行轉(zhuǎn)化。

聚焦七 參數(shù)法探求動點(diǎn)的軌跡方程

例7 (2 0 1 5年廣東卷理)已知過原點(diǎn)的動直線l與圓C：x2+y2-6x+5=0相交于不同的兩點(diǎn)A、B。求線段A B的中點(diǎn)M的軌跡方程。

解析：設(shè)A(x1,y1),B(x2,y2),過原點(diǎn)的動直線為l：y=k x,將動直線l代入圓C：x2+y2-6x+5=0,消去y得(k2+1)x2-6x+5=0。因?yàn)棣?3 6-2 0(1+k2)＞0,所以。設(shè)中點(diǎn)為M(x,y),則x1+x2=除得到。代入消去k,得：

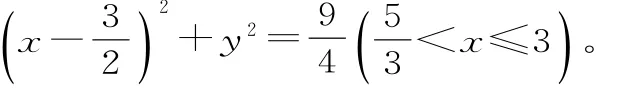
點(diǎn)評：如果直接找不出動點(diǎn)的橫坐標(biāo)x與縱坐標(biāo)y之間的關(guān)系,則可借助中間變量(參數(shù)可能不止一個)使x,y之間建立起聯(lián)系,然后再從所求式子中消去參數(shù),得出動點(diǎn)的軌跡方程。注意題設(shè)參數(shù)隱含的范圍對橫縱坐標(biāo)的限制,如本題由x≤3。

聚焦八 直線和圓錐曲線的位置關(guān)系

例8 (吉林省實(shí)驗(yàn)中學(xué)2 0 1 5-2 0 1 6學(xué)年上學(xué)期期中測試)若雙曲線1(a＞0)的離心率等于2,直線y=k x-1與雙曲線E的右支交于A、B兩點(diǎn)。

(1)求k的取值范圍;

設(shè)A(x1,y1),B(x2,y2),由得(1-k2)x2+2k x-2=0。①

整理得2 8k4-5 5k2+2 5=0,解得k2=

設(shè)C(x3,y3),由(x3,y3)=m(x1+x2,y1+y2)=(45m,8m)。

因?yàn)辄c(diǎn)C是雙曲線上一點(diǎn),

所以8 0m2-6 4m2=1,解得

點(diǎn)評：設(shè)出直線方程或雙曲線方程,聯(lián)立消元后轉(zhuǎn)化成關(guān)于x或y的一元二次方程,利用根與系數(shù)的關(guān)系時,注意曲線的范圍和兩個交點(diǎn)的隱含條件,構(gòu)建不等式組求參數(shù)范圍或整體代入求解弦長的有關(guān)問題。

聚焦九 點(diǎn)差法探究圓錐曲線的中點(diǎn)弦或?qū)ΨQ問題

例9 (2 0 1 5年高考四川卷理科)如圖5,設(shè)直線l與拋物線y2=4x相交于A、B兩點(diǎn),與圓(x-5)2+ y2=r2(r＞0)相切于點(diǎn)M,且M為線段A B的中點(diǎn)。若這樣的直線l恰有4條,則r的取值范圍是( )。

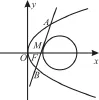
圖5

A.(1,3) B.(1,4) C.(2,3) D.(2,4)

解析：顯然當(dāng)直線l的斜率不存在時,必有兩條直線滿足題設(shè)條件。當(dāng)直線l的斜率存在時,設(shè)斜率為k。設(shè)A(x1,y1),B(x2, y2),x1≠x2,M(x0,y0),則相減得(y1+y2)(y1-y2)=4(x1-x2)。由于x1≠ x2,所以,即k y0=2。圓心為C(5,0),由CM⊥A B得=-1,k y0=5-x0,所以2=5-x0,x0=3,即點(diǎn)M必在直線x=3上。將x=3代入y2=4x得y2=1 2,故-23＜y0＜23。

因?yàn)辄c(diǎn)M在圓(x-5)2+y2=r2(r＞0)上,所以(x0-5)2+y02=r2,r2=y02+4＜1 2 +4=1 6。又y20+4＞4(由于斜率不存在,故y0≠0,不取等號),所4＜y20+4＜1 6,故2＜r＜4。選D。

點(diǎn)評：凡涉及弦的中點(diǎn)或曲線上存在兩點(diǎn)關(guān)于直線對稱問題,常常采用“點(diǎn)差法”將弦的斜率用中點(diǎn)的坐標(biāo)表示。

聚焦十 巧用定義和三點(diǎn)共線的條件求最值

例1 0 (河北省唐山一中2 0 1 6年上學(xué)期期中考試)已知雙曲線的左、右焦點(diǎn)分別為F1、F2,P為雙曲線左支上一點(diǎn), M為雙曲線漸近線上一點(diǎn)(漸近線的斜率大于零),則|P F2|+|PM|的最小值為。

解析：焦點(diǎn)F1(-4,0),F2(4,0),符合題意的漸近線方程為

由雙曲線的定義可知|P F2|-|P F1|= 2a=21 4,所以|P F2|+|PM|=|P F1|+ |PM|+21 4。

作出符合題意的幾何圖形如圖6所示,由圖形可知|P F1|+ |PM|≥|F1M|,所以當(dāng)F1、P、M三點(diǎn)共線時, |P F1|+|PM|的值最小,依據(jù)點(diǎn)F1(-4,0)到直線的距離公式可得此時的最小值為,故所求的最小值為21 4+2。

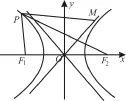
圖6

點(diǎn)評：應(yīng)用曲線的定義及幾何意義求值、求最值等問題在拋物線中很常見,這里列舉了雙曲線的問題,可見知識的應(yīng)用可以拓展。

聚焦十一 構(gòu)建一元目標(biāo)函數(shù)求最值

例1 1 (2 0 1 6年山東省淄博市一模)已知橢圓C：x2+2y2=2。F1、F2分別是橢圓的左、右焦點(diǎn),過F2的直線交橢圓于M、N兩點(diǎn),求的最小值和最大值。

解析：易知右焦點(diǎn)F2(1,0),若直線MN的斜率不存在,則

若直線MN的斜率存在,設(shè)MN的方程為y=k(x-1)。設(shè)M(x1,y1),N(x2,y2),得(2k2+1)x2-4k2x+2k2-2=0。由題設(shè)知恒有兩個交點(diǎn),所以x1+

點(diǎn)評：“過點(diǎn)F2的直線”提示我們用直線為點(diǎn)斜式做題比較方便,既然引入了變量k,目標(biāo)可以通過韋達(dá)定理轉(zhuǎn)化為含k的一元一次分式函數(shù),從而用函數(shù)觀點(diǎn)求最值。為了避免討論斜率還可設(shè)“過點(diǎn)F2的直線為x=m y+1”。

聚焦十二 構(gòu)建二元目標(biāo)函數(shù)求最值

例1 2 動點(diǎn)Q在橢圓C：2x2+y2=5上移動。兩定點(diǎn)為求△A B Q的面積取最大值時點(diǎn)Q的坐標(biāo)。

解析：設(shè)點(diǎn)Q(x0,y0),則有2x20+y20= 5。直線A B的方程為x+2y=0,則點(diǎn)Q到A B的距離

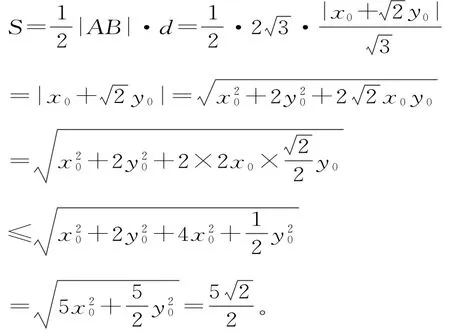
點(diǎn)評：設(shè)出動點(diǎn)Q的坐標(biāo)后,將目標(biāo)轉(zhuǎn)化為二元函數(shù),可以不消元,利用基本不等式,再結(jié)合=5求解。

聚焦十三 通過特殊情況猜想并證得定點(diǎn)或定值

解析：由m+k=0知m=-k,直線l的方程可化為y=k(x-1)。

設(shè)M(x1,y1),N(x2,y2),則：

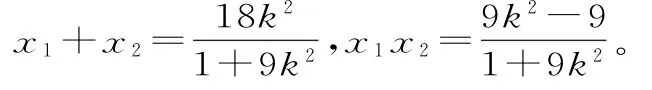
點(diǎn)評：對于探索性問題,我們可先特殊化處理,猜想問題的存在性,再作一般性的證明。這樣處理能為探究提供具體的方向,減少運(yùn)算量。如本題中取k=1探究使問題簡單明朗化。

(責(zé)任編輯 徐利杰)