分離式大懸臂鋼箱梁力學空間效應分析

沈錢斌

（同濟大學建筑設計研究院（集團）有限公司，上海市200092）

分離式大懸臂鋼箱梁力學空間效應分析

沈錢斌

（同濟大學建筑設計研究院（集團）有限公司，上海市200092）

分離式箱形斷面是鋼橋中普遍采用的結構形式，應用于城市高架主線橋時，由于橋下地面道路通行和景觀需求，往往會形成橫向大懸臂結構，力學空間效應明顯。以太原市臥虎山快速路建設工程中某兩跨連續鋼箱梁為例，利用A ba q u s有限元工程模擬軟件建立全橋三維板殼單元模型，分析其在典型荷載下的空間力學性能，包括剪力滯效應、活載偏載效應、支點橫梁應力，并與單梁模型進行對比，為同類橋梁的設計和簡化分析提供參考。

分離式；大懸臂；鋼箱梁；空間效應；有限元

0 引言

在城市高架橋梁的建設中，當需要跨越橫向道路、河流等障礙物時，橋梁施工空間往往會受到限制。在這種情況下，鋼結構橋梁由于可采用預制拼裝的施工工藝，常常會被作為一種極具競爭力的比選方案。城市高架主線橋橋面一般較寬，通常要達到20多米甚至30 m左右。當需要利用橋下空間作為地面道路時，橋墩需設置在道路的中央分隔帶內，分隔帶的寬度一般為8～10 m，因此橋梁在橫向會形成大懸臂結構，懸臂尺寸一般會在10m左右。另外，城市高架橋梁的景觀需求較高，結構線條不宜太笨重。為了使行人在橋下通行時感覺不過于壓抑，橋梁底板也不宜過寬。因此，當選擇鋼箱梁方案時，常常會采用帶大懸臂的箱梁結構。

整體式（單箱多室）斷面的鋼箱梁在城市高架橋中運用較多，其力學性能通過數值模擬的方法已得到較為充分的了解。分離式斷面的鋼箱梁由于其在運輸和經濟方面的優越性，在公路和鐵路橋梁上運用較多。因為其橋下空間往往不受限，可以在橋墩上設置蓋梁并在箱體的下方擺放多個支座，使受力接近于簡單的平面狀態。在城市高架主線橋上應用分離式鋼箱梁時，由于橋下凈空的限制，支座會設置在箱體范圍外，從而形成復雜的空間應力狀態。因此，有必要對該類結構進行深入的空間效應分析，充分了解其受力性能[1]。

1 工程背景

臥虎山快速路是太原北部地區的一條快速通道，其高架主線標準橋寬23.5 m，雙向六車道。主線橋為預應力混凝土連續箱梁，采用大懸臂流線形斷面。主線橋在跨越地面某構筑物時，采用了50 m+50 m的連續鋼箱梁，梁高2.0 m，與混凝土梁同寬，支座橫向間距為5.8m，懸臂。鋼箱梁為雙箱單室分離式斷面，單個箱室頂寬4.1 m，底寬3.6 m，采用斜腹板，兩個箱室的凈距為7.6 m，箱室外的挑臂長度為3.85 m。鋼箱梁縱向間隔2 m設置一道隔板，其中間隔6 m設置一道實腹隔板，其余為空腹隔板。挑臂加勁板間距2 m，加勁板端部高度0.4 m，根部高度1.0 m。空腹隔板處，兩箱室之間的橫隔板高度為1.5 m，空腹隔板及中墩處斷面如圖1所示。

圖1 1/2空腹隔板斷面圖

箱梁頂板厚16mm，在支點處加厚至28mm；底板厚20mm，在支點處加厚至32mm；腹板厚18mm，在支點處加厚至25 mm；橫隔板厚12 mm，在支點處加厚至28 mm。頂板縱向加勁肋主要采用U形肋，在靠近懸臂端部時采用I形肋，底板縱向加勁肋采用I形肋。

2 計算模型建立

計算模型的建立采用A ba q u s有限元工程模擬軟件，其“部件+組裝”的建模方法與鋼結構橋梁的建造方法相似。運用S4R單元（四節點四邊形有限薄膜應變線性減縮積分殼單元）建立全橋三維板殼模型。邊界條件通過軟件的分布耦合功能進行模擬，相比對單個節點進行約束，可以達到既能釋放轉角約束，又不會在支座處出現與實際不相符合的應力集中現象，如圖2所示。鋼材采用Q345qD，材料參數按規范取值。荷載的施加包括鋼箱梁自重、二期荷載和汽車荷載。

圖2 鋼箱梁全橋部件組裝圖及支座底鋼板分布耦合邊界圖

3 鋼箱梁空間力學效應

本文通過空間板殼模型與縱、橫向單梁模型進行的對比分析（單梁模型由M id a s軟件建立），從以下幾個方面來論述鋼箱梁的力學空間效應。

3.1 空間板殼模型與縱向單梁模型的對比

鋼箱梁受力時存在剪力滯效應，即頂、底板應力在斷面上分布不均勻。單梁模型通過翼緣有效寬度或剪力滯系數近似考慮這種影響，可參見《公路鋼結構橋梁設計規范》（J T G D64—2015）（以下簡稱《鋼橋規》）第5.1.8條[4]。空間模型則可以更為直觀地觀察到剪力滯效應，圖3和圖4為板殼模型的兩個控制斷面（中支點處和跨中距邊支點18.5 m處）在恒載作用下的頂底板應力分布圖。

圖3 恒載作用下中支點處頂底板應力分布圖

圖4 恒載作用下距邊支點18.5 m處頂底板應力分布圖

圖3和圖4表明，此類鋼箱梁在中支點處的剪力滯效應明顯，經計算，頂板的剪力滯系數為1.407，底板的剪力滯系數為1.335。距邊支點18.5m處剪力滯效應相對緩和，頂板的剪力滯系數為1.090，底板的剪力滯系數為1.032。剪力滯系數為斷面應力峰值與平均值的比值[2]。

板殼模型和單梁模型的應力對比數據見表1，單梁模型根據規范考慮翼緣有效寬度后，基本與板殼模型接近，并有一定的安全余量。

表1 恒載作用下頂、底板應力MPa

圖5和圖6為板殼模型的兩個控制斷面（中支點處和距邊支點21.5 m處）在汽車荷載作用下的頂底板應力分布圖。實線為六車道橫向左偏工況，虛線為橫向對稱加載，縱向均按影響線最不利工況布置。

圖5 汽車荷載作用下中支點處頂底板應力分布圖

圖6 汽車荷載作用下距邊支點21.5m頂底板應力圖

圖5和圖6表明，在汽車偏載作用下，頂底板的應力峰值將大于對稱加載的工況。在最不利工況下，中墩頂板偏載系數為1.08（偏載工況應力峰值與對稱工況的比值[2]，下同），底板偏載系數為1.12；距邊支點21.5 m處，頂板偏載系數為1.09，底板偏載系數為1.08。可見，本橋雖然寬跨比接近1/2，根據常規工程經驗，橫向偏載系數會大于1.15，但計算發現控制斷面的偏載系數均小于1.15，原因在于該橋橫向剛度比較大的，兩分離箱室間的剛性橫隔板的高度為1.5 m，跨高比為1/5。

3.2 空間板殼模型與縱向單梁模型的對比

大懸臂鋼箱梁的橫向計算內容主要包括橋面板、橫梁內力及懸臂位移等，本文主要針對支點橫梁應力進行分析。支點橫梁的簡化平面分析就是建立橫向單梁模型，對于本橋，支點橫梁即簡化為雙支點的懸臂梁，橫梁截面為頂底板帶翼緣的箱形截面[3]，如圖7所示。

圖7 中支點橫梁單梁模型（單位：MPa）

單梁模型加載時，恒載作為集中力直接加載到腹板位置，汽車荷載通過橫向移動荷載施加。板殼模型的汽車荷載按照支點斷面處應力最不利加載，即在懸臂端部范圍加載2個車道。圖8為單梁模型在汽車荷載的作用下，頂底板最大應力包絡圖。兩種模型的應力對比數據見表2。

圖8 汽車荷載作用下頂底板應力包絡圖（單位：MPa）

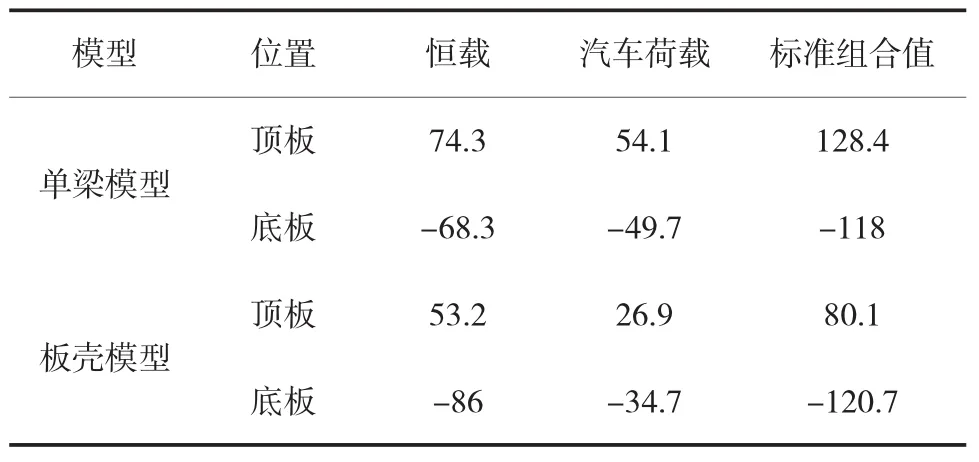
表2 橫梁支座處應力對比表MPa

由表2知，單梁模型由于對荷載加載模式進行了簡化，所以應力值與空間模型存在較大差異，這也跟結構的特點密切相關。對于恒載，單梁模型的頂板應力要高于板殼模型，原因在于前者對頂板寬度的選定比較難把握，本文頂板翼緣寬度取橫隔板間距的1/2；單梁的模型底板應力要小于板殼模型，這個原因主要是對于這種分離式大懸臂結構，橫梁處底板的寬度是有限的，把恒載直接施加在腹板位置偏于不安全。因為挑臂的頂板加勁肋也可以傳遞剪力，且相對于支點的力臂更大，這一點是設計中需要關注的。對于汽車荷載，單梁模型的計算結果總體上是偏保守的，因為跨中汽車荷載的傳遞路徑并非是完全縱向，簡化處理會導致挑臂范圍的應力特別大，這其實是失真的，在計算中一般會忽略此部分的效應。

4 結語

（1）通過對鋼箱梁全橋板殼模型計算分析得到：在恒載及汽車荷載作用下，大懸臂連續鋼箱梁的頂底板會出現剪力滯效應，即頂底板在腹板處的應力會高于其他區域，導致整個斷面上應力分布不均勻。中支點的剪力滯效應尤為明顯，跨中最大正彎矩處斷面剪力滯效應趨于平緩。

（2）根據板殼模型的斷面應力得到：恒載作用下中支點的剪力滯系數頂、底板分別為1.407和1.335，跨中最大正彎矩處分別為1.090和1.032。單梁模型按《鋼橋規》考慮翼緣有效寬度后，頂、底板應力略大于板殼模型，因此通過折減翼緣有效寬度的方法來考慮剪力滯效應對此類結構是合適的。

（3）在汽車偏載作用下，鋼箱梁頂、底板會出現應力不均勻，與常規的混凝土橋梁不同的是，對于寬跨比較大的鋼箱梁，在橫向剛度較大的情況下，偏載系數將小于混凝土橋梁的工程經驗值（即寬跨比不大于1/2時取1.15，大于1/2時取1.25）。

（4）通過對板殼模型和單梁模型的對比分析得到：對于大懸臂分離式鋼箱梁的橫梁計算，單梁模型將恒載施加到腹板位置的簡化方法是不合適的，計算得到的結果對底板應力偏于不安全，建議將一定比例的恒載作為均布荷載施加到懸臂上。另外，在單梁上模擬汽車荷載橫向移動的簡化方法，計算得到頂、底板應力要比板殼模型大40%～100%，而且懸臂下翼緣的壓應力是失真的，因此對此類結構的橫梁進行空間應力分析是必要的。

[1]吳沖.現代鋼橋[M].北京：人民交通出版社，2006.

[2]魏華.大懸臂弧形腹板鋼箱梁剪力滯效應和偏載效應分析[J].上海公路，2012（3）：49-52.

[3]熊禮鵬.寬箱連續鋼箱梁橋支點橫梁空間受力分析[J].交通科技，2014（2）：1-3.

[4]J T G D64—2015,公路鋼結構橋梁設計規范[S].

U441

A

1009-7716（2017）06-0084-03

10.16799/j.cnki.csdqyfh.2017.06.024

2017-03-07

沈錢斌（1981-），男，上海人，工程師，從事橋梁設計工作。