基于改進蟻群算法的焊接機器人路徑規劃

金嘉琦，劉暢，徐振偉

基于改進蟻群算法的焊接機器人路徑規劃

金嘉琦，劉暢，徐振偉

(沈陽工業大學機械工程學院，遼寧沈陽110870)

為了解決目前車身焊接機器人路徑規劃不合理的情況，分析了焊接機器人運動過程，建立了有效的路徑規劃數學模型。通過對蟻群算法的研究，將遺傳算法的遺傳算子理論引入蟻群算法，運用MATLAB編寫相應的程序。結果表明，改進蟻群算法能夠更好的適用于路徑規劃，能夠規劃出一條合理的焊接路徑。

焊接機器人;路徑規劃;改進蟻群算法

0 前言

近年來，隨著汽車產業的蓬勃發展，國內絕大多數汽車制造廠商都引進工業機器人來提高生產質量和效率。在汽車的生產中，工業機器人被廣泛應用到汽車制造的各個方面，尤其是白車身的焊接方面，機器人以其高質量、高效率和節省勞動力的優點得到各大汽車廠商的青睞。但據統計，每臺汽車車身焊點多達4 000～5 000個，分配到每臺機器人的焊點也多達幾百個，現在人工為主的機器人路徑規劃缺少理論的認證，存在很大的隨機性，沒有一個系統的方案，如何高效率的完成焊接，規劃出一條節省機器人工位生產時間、提高生產質量的路徑成為目前需要解決的問題［1］。

對于焊接機器人在路徑規劃方面的不合理情況，本文通過對蟻群算法的研究，運用改進的蟻群算法建立路徑規劃的數學模型，采用MATLAB軟件編寫相應程序，規劃出一條三維空間下的最短路徑，最終達到減少機器人工位的生產時間和配合整體工時的目的。

1 路徑規劃的數學模型

在實際的汽車生產車間，完成一輛白車身的焊接需要多臺機器人協同工作，一般情況下為3～4臺，一臺抓取工件，其它工位負責焊接，以加快生產時間。本文研究的是已經完成焊點分組，負責車門焊接的單臺機器人的路徑規劃。

在焊接機器人工作過程中，機器人手持焊槍從所設定的HOME點出發，從第一個焊點開始，依次焊接，完成一個循環回到HOME點。這與求解TSP問題非常相似，TSP即旅行商問題，旅行者想要在幾個城市之間旅行，出發前制定一個系統的旅行方案，從所在城市出發，游玩所有城市后，回到自己所在城市，達到所用路程或時間最短的問題。

機器人在兩個焊點之間的運動是以PTP的形式實現，也是速度最快的方式，在焊槍和夾具有干涉的情況下，增加過度點使機器人快速通過障礙。因此，縮短整體工位時間的方式即是減少機器人作業的路程。所以，本文以在焊接機器人在三維焊點之間所走路程最短作為評價準則，其數學模型可表示為:

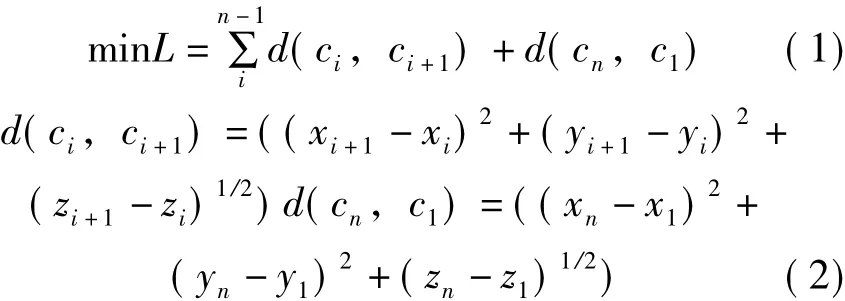
式中，n為車身焊點的個數;d(ci，ci+1)為兩個焊點之間的距離。

2 基于改進蟻群算法的路徑規劃

蟻群算法的構思來自與自然界螞蟻群體的覓食行為，是一種新興的啟發式仿生進化算法，因其簡單、高效率等優點被廣泛應用［2］。螞蟻在尋找食物過程中，會有目的的釋放一種信息素來告知后面的螞蟻距離食物的最短路徑，路徑越短，走過的螞蟻越多，信息素濃度越大，因此形成一種正反饋機制。本文采用改進蟻群算法，將遺傳算法的遺傳算子理論引入蟻群算法，使蟻群算法收斂更快，結果更優，更加適用于路徑規劃。

2.1 初始信息素設置

在蟻群算法中，初始信息素值設置太小，會導致算法提早進入局部最優，但是，初始值太大，會增加算法的計算量，不易于求解，本文采用如下公式進行設置，

式中，n為焊點的個數;Lnm是由最近的鄰域啟發產生的一個路徑長度。

2.2 螞蟻在焊點間的轉移規則

螞蟻在運動過程中，由其中一個焊點走到下一個焊點并不是隨機的，而是根據各焊點之間路徑上的信息素濃度來決定轉移方向，本文采用的轉移規則為隨機比例規則，它給出了位于焊點i的螞蟻k在選擇移動到焊點j的概率。在t時刻，螞蟻k在焊點i選擇焊點j的轉移概率為

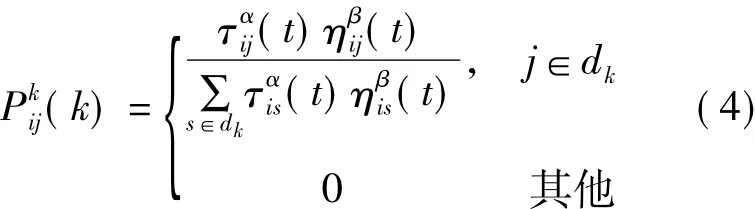
式中，dk={0，1，…，n－1}，表示編號為k的螞蟻下一步允許選擇的焊點;ηij為能見度因數，其值為兩焊點之間距離倒數，即ηij=1/dij;α為信息啟發因子;β為期望啟發因子;α和β分別反映螞蟻在運動過程中所積累的信息和啟發信息在螞蟻選擇路徑中的相對重要性。

2.3 信息素更新方案

螞蟻完成一次循環后，對螞蟻所走的路徑上的信息素濃度進行全局更新，為了避免信息素無限累加，采用蟻周系統進行信息素更新。

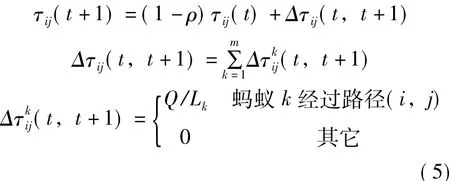
式中，Δτij(t，t+1)表示更新螞蟻k走過的路徑;ρ為信息素揮發系數(0＜ρ＜1);Lk為螞蟻k在本次循環中所走的路徑長度。

2.4 交叉算子

遺傳算法的交叉算子可以產生新的個體，維持種群多樣性，增強算法的全局搜索能力［3］。當所有的螞蟻訪問完所有的焊點以后，對螞蟻群體生成的解(螞蟻走過路徑)進行交叉，用以生成更優質的種群。本文采用順序交叉方法，基于概率Pc先選擇兩個父代螞蟻進行雙點交叉，再進行維持原有訪問順序的巡回路線修改(與已有編碼不重復)，具體如下所示:

父代A:56︱2398︱714

父代B:14︱3269︱758

子代A1:3269︱58714

子代B1:2398︱14675

2.5 變異算子和算子更新

變異算子決定算法的局部搜索能力，與交叉算子配合，使其算法具有良好的搜索性能［3］。對交叉產生的新種群進行變異操作，文章采用插入式變異方法，即隨機產生兩個變異位置，將第二個變異位插入到第一個變異位前面，如圖1所示。變異操作是由變異概率Pm來進行控制。通過對評價函數的比較進行算子更新，如果變異結束后，子代解不如父代，則仍采用父代解。

2.6 算法流程

基于改進蟻群算法的焊接機器人路徑規劃算法流程如圖2所示。

3 運用MATLAB仿真

基于以上算法，運用MATLAB軟件編寫相應程序，由于蟻群算法是一種概率算法，其需要設置的參數比較多，很難找到一種數學算法計算每個參數的最優值［4］，通過查閱文獻和實驗可確定各參數初始值設置為:螞蟻數量m=20，α =1，β=1，ρ=0.05，交叉概率Pc=0.7，變異概率Pm=0.3。輸入各車門焊點坐標，通過實驗發現，經過100次迭代后可求得最優路徑，如圖3所示。

從圖中看出，輸出圖形為一條封閉路徑，符合機器人工作要求，最優路徑結果為:1－5－17－18－16－11－10－6－4－3－2－7－8－9－12－15－14－13－19－22－20－21，最優路徑距離為755.107。

4 結論

本文通過對機器人運動狀態的分析，建立了求解焊接機器人路徑規劃的數學模型，采用改進蟻群算法，運用MATLAB軟件編寫程序，對其數學模型進行優化仿真，結果表明，通過規劃后的路徑符合機器人的工作要求，對于提高機器人的加工效率，節省加工時間有一定的意義，為焊接機器人路徑規劃提供了一個新的方法。

［1］彭永健，李小寧．基于蟻群算法的分組焊點焊接路徑優化方法研究［J］．機械制造與自動化，2012 (01):6－9．

［2］楊學峰．蟻群算法求解TSP問題的研究［D］．吉林:吉林大學，2010．

［3］雷英杰，張善文．MATLAB遺傳算法工具箱及應用［M］．西安:西安電子科技大學出版社，2014．

［4］李士勇．蟻群算法及其應用［M］．哈爾濱:哈爾濱工業大學出版社，2004．

［5］魏安立，胡小建，孫太生．基于遺傳算法焊接機器人路徑規劃研究［J］．現代焊接，2011(08):27 +29．

［6］林巨廣，陳甦欣，戴淮初，等．蟻群算法在白車身底板焊接路徑規劃中的應用［J］．焊接學報，2015．

Path planning of welding robot based on improved ant colony optimization

JIN Jia-qi，LIU Chang，XU Zhen-wei
(School of Mechanical Engineering，Shenyang University of Technology，Shenyang 110870，China)

In order to solve the situation that path planning of welding robot for automobile body is not reasonable，this paper analyzed of the welding robot motion process，established a mathematical model of effective path planning．Through studying ant colony optimization，the genetic operator theory of genetic algorithm was introduced into the ant colony optimization，and the corresponding program was prepared using by MATLAB．The results show that the improved ant colony optimization can better apply to path planning and plan out a reasonable welding path．

welding robot;path planning;improved ant colony optimization

TG457

A

1001－196X(2017)01－0044－03

2016－07－07;

2016－09－29

金嘉琦(1955－)，男，博士，教授，博士生導師，主要研究方向:精密加工與精密測量的理論與技術研究。

劉暢(1992－)，男，碩士研究生，主要研究方向:工業機器人技術。