熱傳導方程的完美匹配層公式及其穩定性分析

王小花，潘文峰

熱傳導方程的完美匹配層公式及其穩定性分析

王小花，潘文峰

(武漢理工大學理學院，湖北武漢430070)

為了求解無界空間中的熱傳導方程，基于Laplace變換，引入若干個輔助變量，提出了一個熱傳導方程的完美匹配層(PML)公式。通過分析偏微分算子特征值實部的符號和特征向量的完備性，得到了PML方程的穩定性。在二維空間中，常系數PML方程的柯西問題是弱穩定;在三維空間中，常系數PML方程的柯西問題是強穩定。數值實驗結果表明:熱傳導方程PML公式的絕對誤差最大值大約是1.5×10－3，經典Dirichlet邊界條件和Neumann邊界條件的絕對誤差最大值大約是2.5×10－2和3.0×10－2。因此，熱傳導方程PML公式可以顯著提高數值解的準確性。

熱傳導方程;完美匹配層;穩定性;輔助變量;Laplace變換

0 引言

熱量在無界介質中的傳播是一個重要而又基本的問題。對于波的傳播問題，完美匹配層(perfectly matched layer，PML)算法［1］已經被證明是一種有效且精確的方法。基于二維傅里葉變換，文獻［2］推導出了一個關于對流擴散方程的PML公式，并且證明了在吸收層的外邊界，反射是非常小的。同時，數值實驗也驗證了完美匹配層算法的有效性和準確性。對于波方程，目前有多種非常有效的PML算法，例如輔助微分方程完美匹配層(auxiliary differential equation perfectly matched layer，ADE-PML)算法［3］和復頻移完美匹配層(complex frequency shifted perfectly matched layer，CFS-PML)算法［4］。對于依賴時間的熱傳導方程，方程的穩定性是非常重要的，不穩定的數值方法可能會導致計算區域內的數值解被污染。已經有很多學者研究了偏微分方程的穩定性［5－8］，然而，關于熱傳導問題的完美匹配層算法的研究還比較少，特別是類似于波方程的ADE-PML算法。本文基于Laplace變換，引入若干個輔助變量，嘗試推導出一個適用于熱傳導方程的ADE-PML算法，以期提高數值解的準確性，并針對熱傳導方程的PML公式進行穩定性分析。

1 PML公式

考慮一個溫度場u在一個無界的三維空間中進行傳導，并假設所有的熱源初始分布集中在一個給定的區域Ω=［－a1，a1］×［－a2，a2］×［－a3，a3］，a1，a2，a3＞0，因此，在區域Ω內部，溫度場u(x1，x2，x3，t)滿足如下方程:

本文希望截斷無界區域并將計算限制在有限的區域Ω內部。因此，假設Ω被包含于一個厚度為Li(i=1，2，3)的PML，其中Li(i=1，2，3)為在xi(i=1，2，3)方向的厚度。在吸收層的內部，溫度場u滿足一個修正的無熱源的以指數速度衰減的熱傳導方程。

類似于文獻［5，9－10］，設u^表示u的Laplace變換，定義如下:

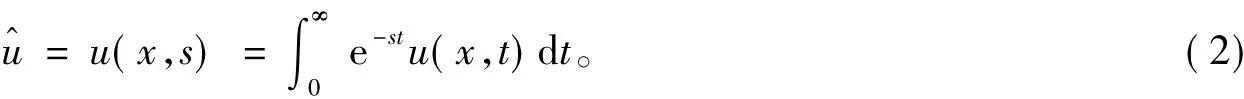
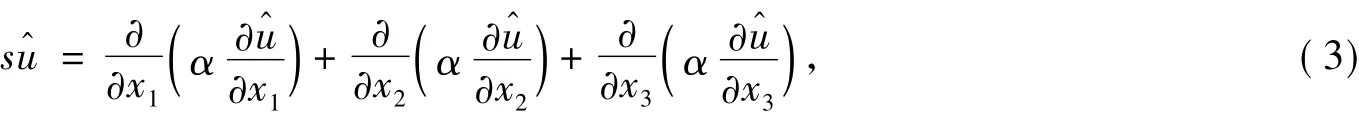
引進坐標變換

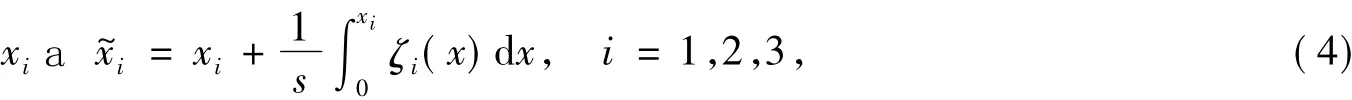
在區域Ω之外，u^滿足如下方程:

其中:ζi在吸收層xi＞ai是正的，在Ω內部是0。若要求u^滿足如下的方程

顯然u在Ω的內部保持不變，但是在吸收層內呈指數衰減。

文獻［5］在Laplace變換域上給出了雙曲拋物系統標準的PML算法，但是涉及到了太多的輔助變量。本文嘗試使用較少的輔助變量，推導出一個新的關于熱傳導方程的PML公式。

由坐標變換式(4)可知:

設γi=γi(ζi;s)，i=1，2，3，則:

根據式(6)可得:

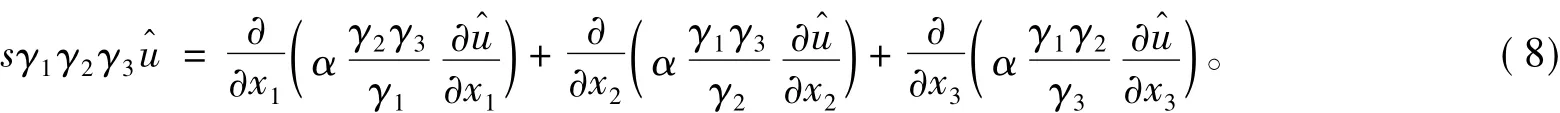
根據式(7)，可以得到如下的恒等式:

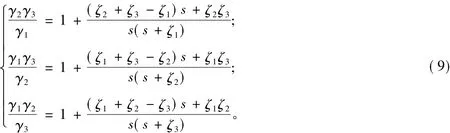
結合式(8)和式(9)，可得:

接下來，引進一些輔助變量:

使用Laplace逆變換將方程(10)變換回時域，可得:

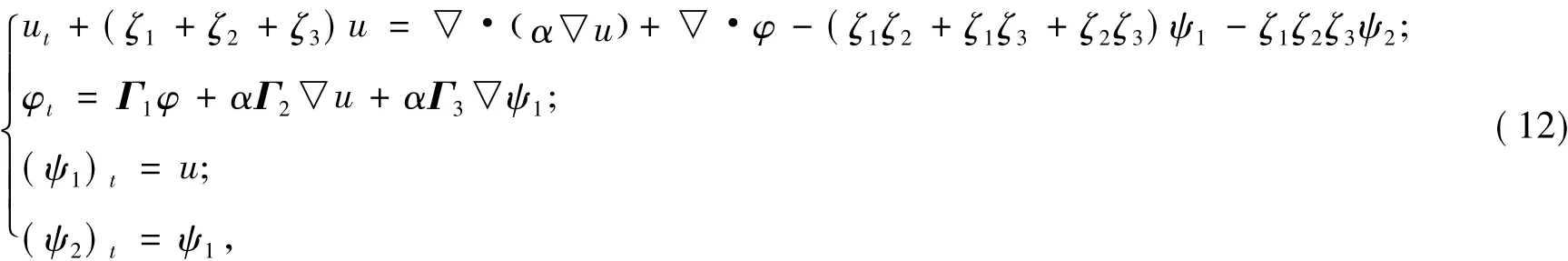
其中:

在Ω內部，吸收函數ζi(i=1，2，3)和輔助變量φ取值為0，因此，方程(12)又簡化成了方程(1)。可以看到:該PML公式只需要5個輔助變量φ1，φ2，φ3，ψ1，ψ2，并且沒有涉及到高階導數，算法的實現更加簡單。

類似的推導可知，在二維空間中不存在變量ψ2，φ3，ζ3，此時PML方程簡化成如下形式:

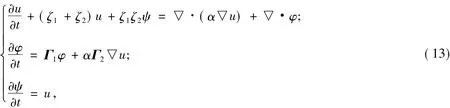
其中:

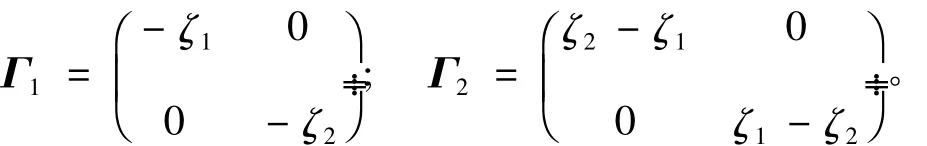
2 穩定性

本節中，將依次討論二維和三維情況下PML公式的穩定性。對于拋物系統的穩定性，文獻［11］有比較詳細的介紹，本文將引用文獻［11］中相關的理論證明方程(12)和方程(13)的穩定性。

考慮一個一般的偏微分方程的柯西問題:

根據文獻［11］可知:柯西問題的適定性和穩定性，可以通過算子P(iω)的特征值和特征向量來判斷。下面給出一個關于判別適定性和穩定性的充要條件。

引理1［11］若存在不依賴于ω的常數C＞0(resp.C=0)使得算子P(iω)的所有特征值λ滿足:

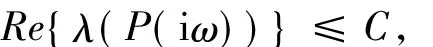
則柯西問題(14)是弱適定的(resp.弱穩定的)。若對應的特征向量是完備的，則柯西問題(14)是適定的(resp.穩定的)。

利用以上的穩定性理論，可以得到下面兩個穩定性定理。

定理1在二維空間中，對于任意的ζ1，ζ2＞0，若ζ1=ζ2，則PML公式的初值問題是弱穩定的。

證明設U=(u，φ1，φ2，ψ)T，可以將PML方程(13)寫成如下形式:

其中:

設T=det(λI－P1(iω))，則:

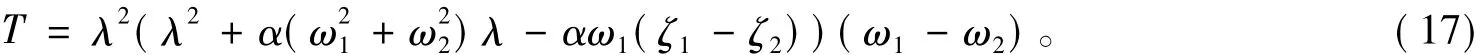
由式(17)可知:只有ζ1=ζ2才能判斷PML方程的穩定性。此外，當ζ1=ζ2時，矩陣E不可對角化，因此PML方程是弱穩定的。

定理2在三維空間中，對于任意的ζ1，ζ2，ζ3＞0，PML公式的初值問題是強穩定的。

證明令U=(u，φ1，φ2，φ3，ψ1，ψ2)，則可將式(12)寫成如下形式:

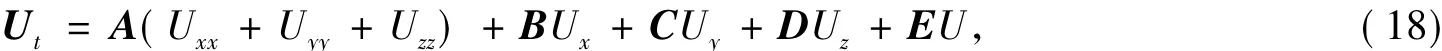
其中:

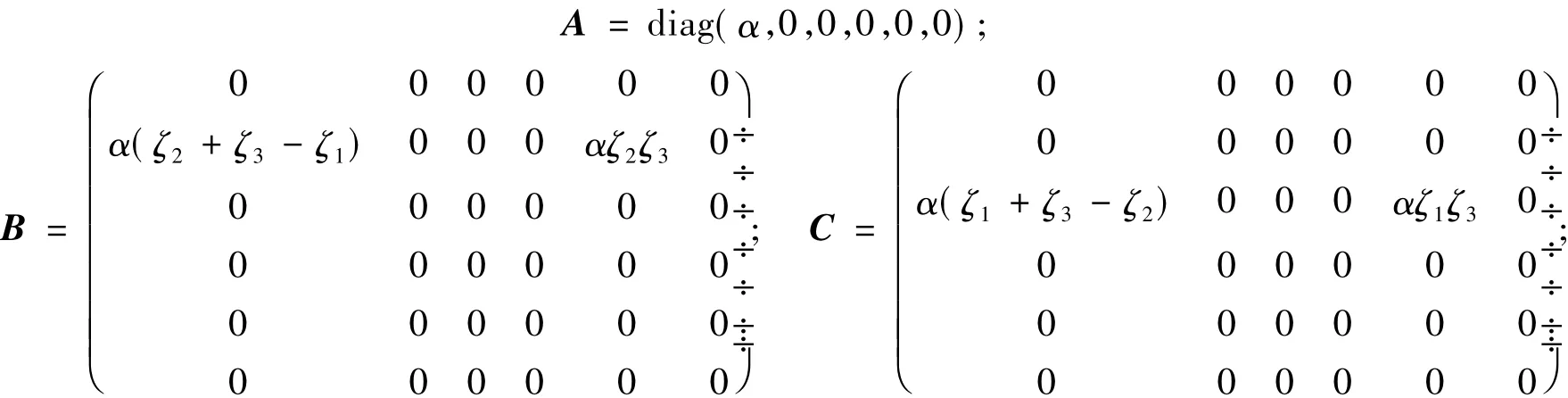
因此，P(iω)的所有特征值的實部小于等于0，同時，矩陣E可對角化，故在三維空間中，對于任意的ζ1，ζ2，ζ3＞0，PML公式的初值問題是強穩定的。

3 數值實驗

本節通過具體的數值算例說明具有輔助微分方程的完美匹配層方法的有效性，并與經典的狄利克雷(Dirichlet)邊界條件和紐曼(Neumann)邊界條件的結果相比較。考慮如下的初值問題:

其中:u0(x1，x2)=為初始的熱量分布，并且參數α=1。此時，初值問題(20)具有解析解

對應的PML設置如下:

其中:n=6;ζ=100;計算區域Ω=［－2，2］2;吸收層厚度L1=L2=0.3。對于對應的PML方程，本文使用標準的有限元方法求解，采用線性基函數，網格的最大尺度是0.1，在PML吸收層的外邊界，采用齊次的Dirichlet邊界條件。

當t=0.7時，不同的邊界條件所對應的絕對誤差，如圖1所示。從圖1可以看出:PML邊界條件的絕對誤差最大值大約是1.5×10－3(見圖1a)，經典的Dirichlet邊界條件和Neumann邊界條件的絕對誤差最大值分別約為2.5×10－2和3.0×10－2(見圖1b和圖1c)，因此，PML方法可以顯著提高數值解的準確性。為了進一步說明PML邊界條件對原方程的影響，取t=0.7，x1=0，此時，數值解和解析解的差別如圖2所示。

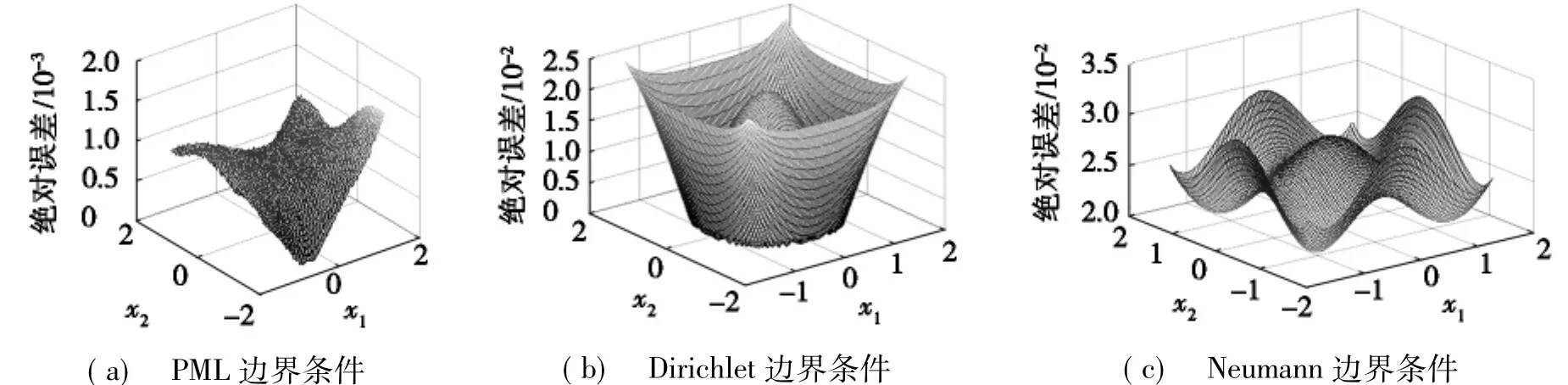
圖1 不同邊界條件的絕對誤差

從圖2可以看出:在內部區域，數值解和解析解幾乎完全重合;在吸收層內部，u迅速衰減，到達吸收層的外部時幾乎為0，與波方程的結果類似。

4 結論

本文推導出了一個熱傳導方程的PML公式，與文獻［5］中關于雙曲拋物系統的PML公式相比，本文的PML公式使用了較少的輔助變量。此外，證明了PML方程的柯西問題的穩定性。在二維空間中，常系數的完美匹配層方程的柯西問題是弱穩定的;在三維空間中，常系數的完美匹配層方程的柯西問題是強穩定的。通過數值實驗驗證了熱傳導方程PML公式可以顯著提高數值解的準確性。

［1］DRUSKIN V，GTTEL S，KNIZHNERMAN L.Near-optimal perfectly matched layers for indefinite Helmholtz problems［J］.Mathematics，2015，58(1):686－710.

［2］LANTOS N，NATAF F.Perfectly matched layers for the heat and advection-diffusion equations［J］.Journal of computational physics，2010，229(24):9042－9052.

［3］ATLURI S N，MARTIN R，KOMATITSCH D，et al.A high-order time and space formulation of the unsplit perfectly matched layer for the seismic wave equation using auxiliary dfferential equations(ADE-PML)［J］.Computer modeling in egineering＆sciences，2010，56(1):17－40.

［4］MA Y，CHEN S W，LU F，et al.The CFS-PML for 2-D WLP-FDTD method of dispersive materials［J］.International journal of applied electromagnetics and mechanics，2016，51(4):349－361.

［5］APPELD，HAGSTROM T，KREISS G.Perfectly matched layers for hyperbolic systems:general formulation，wellposedness，and stability［J］.SIAM journal on applied mathematics，2006，67(1):1－23.

［6］楊彩虹，胡志興.一類具有飽和發生率的SEIR模型的穩定性［J］.河南科技大學學報(自然科學版)，2017，38(1): 78－83.

［7］COHEN G C，LIU Q H.Higher-order numerical methods for transient wave equations［J］.Springer，2002:349－354.

［8］劉俊利，劉璐菊.具有媒體報道的傳染病模型穩定性［J］.河南科技大學學報(自然科學版)，2016，37(2):88－91.［9］SJGREEN B，PETERSSON N A.Perfectly matched layers for Maxwell’s equations in second order formulation［J］.Journal of computational physics，2004，209(1):19－46.

［10］ABARBANEL S，GOTTLIEB D，HESTHAVEN J S.Long time behavior of the perfectly matched layer equations in computational electromagnetic［J］.Journal of scientific computing，2002，17(1):405－422.

［11］KREISS H O，LORENZ J.Initial-boundary value problems and the Navier-Stokes equations［M］.London:Academic Press

Inc，1989:44－62.

O193

A

1672－6871(2017)05－0070－06

10.15926/j.cnki.issn1672－6871.2017.05.015

國家自然科學基金項目(11601402);湖北省自然科學基金項目(2014CFB865)

王小花(1990－)，女，河南信陽人，碩士生;潘文峰(1964－)，男，湖北天門人，教授，博士，碩士生導師，主要研究方向為偏微分方程數值解.

2016－12－21