數(shù)學(xué)基本活動經(jīng)驗主成分和層次水平劃分研究

郭玉峰，張 芳

?

數(shù)學(xué)基本活動經(jīng)驗主成分和層次水平劃分研究

郭玉峰1，張 芳1，2

（1．北京師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院，北京 100875；2．浙江大學(xué)附屬中學(xué)，浙江杭州 310000）

在文獻(xiàn)分析和調(diào)查研究基礎(chǔ)上，給出了數(shù)學(xué)基本活動經(jīng)驗構(gòu)成要素的研究假設(shè)，通過自編測試卷進(jìn)行題目測試，借助因素分析找出了數(shù)學(xué)基本活動經(jīng)驗的4個主成分，分別是歸納概括、類比推廣、數(shù)學(xué)表達(dá)、證明；借助聚類分析得到數(shù)學(xué)基本活動經(jīng)驗的層次水平劃分．

數(shù)學(xué)基本活動經(jīng)驗；主成分；層次水平劃分

1 引 言

2014年教育部頒發(fā)了系列文件，全面深化課程改革、落實立德樹人的根本任務(wù)[1]．其中一項重要舉措是研究、制訂學(xué)生發(fā)展核心素養(yǎng)體系，包括數(shù)學(xué)學(xué)科的核心素養(yǎng)．

學(xué)生數(shù)學(xué)核心素養(yǎng)的養(yǎng)成需要相應(yīng)的知識儲備、能力發(fā)展，尤其積累一定的數(shù)學(xué)基本活動經(jīng)驗，由此帶動了一系列相關(guān)研究[2~4]．2011年義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)正式提出數(shù)學(xué)基本活動經(jīng)驗的課程目標(biāo)，得到數(shù)學(xué)家、數(shù)學(xué)教育研究者、中小學(xué)數(shù)學(xué)教師的廣泛關(guān)注和肯定，數(shù)學(xué)基本活動經(jīng)驗研究日益成為關(guān)注的焦點和討論的熱點．就目前研究看，更多集中在如何認(rèn)識數(shù)學(xué)基本活動經(jīng)驗及其與數(shù)學(xué)基礎(chǔ)知識、數(shù)學(xué)基本思想、數(shù)學(xué)問題提出等的關(guān)系[5~7]、數(shù)學(xué)基本活動經(jīng)驗的分類及特點[8]、數(shù)學(xué)基本活動經(jīng)驗的教學(xué)策略[9]、信息技術(shù)與學(xué)生數(shù)學(xué)基本活動經(jīng)驗積累[10]，等等．有關(guān)數(shù)學(xué)基本活動經(jīng)驗的更深入研究，如數(shù)學(xué)基本活動經(jīng)驗構(gòu)成的主成分分析及其層次水平劃分的研究還較少，而這對一線教學(xué)和數(shù)學(xué)學(xué)科核心素養(yǎng)的深入探討是非常重要的．

郭玉峰、史寧中在文[11~13]中已經(jīng)系統(tǒng)闡述了為什么在義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)中明確提出數(shù)學(xué)基本活動經(jīng)驗，數(shù)學(xué)基本活動經(jīng)驗的內(nèi)涵和維度劃分，針對初中學(xué)生的問卷測試結(jié)果給出了數(shù)學(xué)基本活動經(jīng)驗的不同層次水平劃分等．這些研究在一定程度上刻畫了數(shù)學(xué)基本活動經(jīng)驗的要素組成和層次水平，但維度劃分的幾個方面：觀察聯(lián)想、歸納猜想、數(shù)學(xué)表達(dá)、驗證或證明主要基于文獻(xiàn)分析和理論研究給出；層析水平劃分是針對初中學(xué)生，結(jié)合文獻(xiàn)分析給出的．如何進(jìn)一步完善這些要素？這是要解決的主要問題．針對高中學(xué)生，擬在已有研究的基礎(chǔ)上界定內(nèi)涵、進(jìn)行文獻(xiàn)分析和一線教師調(diào)研，給出數(shù)學(xué)基本活動經(jīng)驗的維度劃分假設(shè)，進(jìn)行測試研究，通過因素分析研究數(shù)學(xué)基本活動經(jīng)驗的主成分、借助聚類分析研究數(shù)學(xué)基本活動經(jīng)驗層次水平劃分，完善數(shù)學(xué)基本活動經(jīng)驗的量表．

2 研究設(shè)計和研究假設(shè)

2.1 研究設(shè)計

數(shù)學(xué)基本活動經(jīng)驗是一個復(fù)雜、內(nèi)隱的心理品質(zhì)，如何刻畫其要素和水平劃分是一件困難的事情．主要參考蘇聯(lián)心理學(xué)家克魯捷茨基對中小學(xué)生數(shù)學(xué)能力的研究．因為能力是直接影響活動效率，并使活動順利完成的個性心理品質(zhì)[14]，這兩者的研究方法有一定共通之處．克魯切茨基于1955—1966年主要進(jìn)行了數(shù)學(xué)能力的結(jié)構(gòu)及其形成等研究．關(guān)于數(shù)學(xué)能力結(jié)構(gòu)的研究主要分為以下幾步：第一步：給出數(shù)學(xué)能力的成分假設(shè)．通過分析文獻(xiàn)、數(shù)學(xué)家和物理學(xué)家的傳記、觀察對數(shù)學(xué)有天賦的兒童、分析中小學(xué)數(shù)學(xué)課程等，給出數(shù)學(xué)能力的成分假設(shè)；第二步：根據(jù)假設(shè)編制測試題對學(xué)生進(jìn)行測試，用因素分析等統(tǒng)計方法給出數(shù)學(xué)能力的不同組成要素；第三步：根據(jù)題目特征、學(xué)生解題過程，對共同因素進(jìn)行命名．此外，也參考了國內(nèi)李洪玉，林崇德[15]、郭玉英[16]等研究中學(xué)生空間認(rèn)知能力、物理思維能力結(jié)構(gòu)成分的思路和方法．研究設(shè)計可用圖1表示．

圖1 研究設(shè)計框架

數(shù)學(xué)基本活動經(jīng)驗盡管是內(nèi)隱的，但長期積淀后往往以某種習(xí)慣表現(xiàn)出來，如思維習(xí)慣、行為習(xí)慣、情感表現(xiàn)等．?dāng)?shù)學(xué)基本活動經(jīng)驗只針對學(xué)生的數(shù)學(xué)思維習(xí)慣，是學(xué)生長期經(jīng)歷數(shù)學(xué)思維活動過程中積累的數(shù)學(xué)思考問題的方式或思考問題的習(xí)慣．

2.2 研究假設(shè)

如同數(shù)學(xué)能力的研究，數(shù)學(xué)基本活動經(jīng)驗構(gòu)成成分的假設(shè)基于兩方面：分析數(shù)學(xué)家的創(chuàng)造過程；借助中學(xué)一線數(shù)學(xué)教師的調(diào)研．

2.2.1 數(shù)學(xué)家進(jìn)行數(shù)學(xué)創(chuàng)造的思考過程

數(shù)學(xué)家進(jìn)行數(shù)學(xué)創(chuàng)造時，會有怎樣的思考習(xí)慣？一些數(shù)學(xué)家表示，他們在進(jìn)行數(shù)學(xué)思考時經(jīng)常會出現(xiàn)“頓悟”，百思不得其解的問題突然有了“答案”，這不是純機(jī)遇，往往需要有意識的努力．也即，數(shù)學(xué)創(chuàng)造發(fā)明的過程需要經(jīng)歷準(zhǔn)備、醞釀、頓悟、整理階段[17]．準(zhǔn)備階段是努力進(jìn)行有意識的數(shù)學(xué)思考，盡管往往以失敗告終，但卻為醞釀和頓悟階段提供了條件．醞釀階段是進(jìn)行無意識的數(shù)學(xué)思考，“無意識不僅要擔(dān)當(dāng)起構(gòu)造各種各樣的思想組合的復(fù)雜任務(wù)，而且還要根據(jù)我們的審美原則去作最細(xì)微和最本質(zhì)的選擇”[17]．醞釀階段是無意識將數(shù)學(xué)知識聯(lián)系到一起，領(lǐng)悟最本質(zhì)關(guān)系或拓展問題的過程．整理階段是用符號等數(shù)學(xué)語言表達(dá)頓悟的結(jié)果并加以證明等，是有意識的數(shù)學(xué)思考過程．由此，數(shù)學(xué)家進(jìn)行數(shù)學(xué)創(chuàng)造時往往經(jīng)歷：發(fā)現(xiàn)相距很近或很遠(yuǎn)事物間的聯(lián)系（包括共性、特性和關(guān)系），尋找本質(zhì)，用數(shù)學(xué)符號進(jìn)行表達(dá)并證明結(jié)論．也即，這個過程一般可以表述為：準(zhǔn)備（觀察、分類比較、歸納概括、類比等）、醞釀（聯(lián)想）、頓悟（領(lǐng)悟本質(zhì)）、整理（數(shù)學(xué)表達(dá)、證明等）．

2.2.2 中學(xué)一線教師認(rèn)為會數(shù)學(xué)思考的學(xué)生的特點

進(jìn)一步調(diào)研、訪談了69名中學(xué)一線數(shù)學(xué)教師，請他們回答“會數(shù)學(xué)思考的學(xué)生的主要特點是什么？”，調(diào)研得到的主要結(jié)果見表1．

表1 調(diào)研的主要結(jié)果

2.2.3 數(shù)學(xué)基本活動經(jīng)驗構(gòu)成成分的假設(shè)

基于以上，結(jié)合教學(xué)實踐，學(xué)生積累數(shù)學(xué)基本活動經(jīng)驗很重要的方面是積累數(shù)學(xué)思維活動經(jīng)驗，即在經(jīng)歷數(shù)學(xué)思維活動的過程中，體驗和感悟數(shù)學(xué)思考的過程，形成合理、正確的數(shù)學(xué)思考問題的方式或習(xí)慣．為此，數(shù)學(xué)基本活動經(jīng)驗構(gòu)成成分的假設(shè)確定為：（1）觀察；（2）比較；（3）數(shù)學(xué)表達(dá)；（4）歸納；（5）類比；（6）證明；（7）聯(lián)想；（8）分類．

3 基于因素分析和聚類分析的數(shù)學(xué)基本活動經(jīng)驗研究

對以上8個研究假設(shè)，進(jìn)一步編制測試題，通過因素分析尋求主成分，借助聚類分析給出層次水平劃分．

3.1 編制測試題

測試問卷的研制經(jīng)歷了大半年的時間，期間查閱大量高中數(shù)學(xué)題、高考題和競賽題，并和中學(xué)一線數(shù)學(xué)教師交流，不斷調(diào)整，最終完成了編制工作．預(yù)測于2014年8月在安徽某省示范高中高三某班進(jìn)行，預(yù)測問卷30份，測試時間2小時．根據(jù)預(yù)測結(jié)果，調(diào)整了2道得分非常低的題目、更換學(xué)生只憑記憶就能作答的一題，最終問卷有22題．8個研究假設(shè)對應(yīng)的題目如表2．

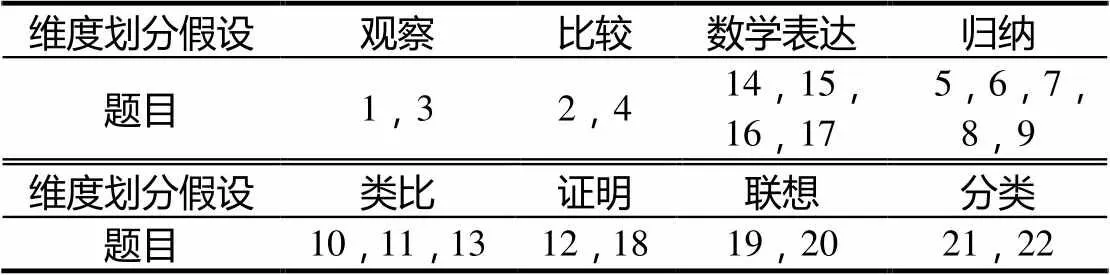
表2 研究假設(shè)及相應(yīng)測試題目

3.2 測試的實施及問卷信與效度分析

正式測試集中在2014年9月，測試時間2小時．選取安徽、貴陽、唐山3所省級示范高中的高三年級，各省選取一個班．發(fā)放問卷138份，剔除空白卷，樣本共計120人．

采用內(nèi)容效度，利用SPSS軟件，計算各研究假設(shè)得分與總分之間的相關(guān)性，如表3．

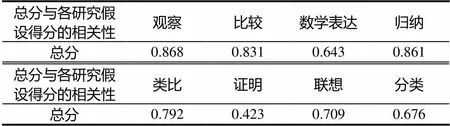
表3 各研究假設(shè)得分與總分的相關(guān)性

總分與各研究假設(shè)的得分之間均顯著相關(guān)，試題具有良好的效度．

3.3 基于因素分析的數(shù)學(xué)基本活動經(jīng)驗主成分研究

對于8個基本假設(shè)，希望通過主成分分析，用更少一些不相關(guān)的指標(biāo)代替具有一定相關(guān)關(guān)系的指標(biāo)，同時又能盡可能多地反映原來指標(biāo)的信息量[19]，即找出數(shù)學(xué)基本活動經(jīng)驗的主成分．首先，采用KMO和球形Barlett檢驗進(jìn)行因子分析的適用性檢驗．用SPSS軟件生成KMO和Bartlett球形檢驗表，見表4．

表4 KMO和Bartlett的檢驗

KMO檢驗測試值為0.826，說明各研究假設(shè)的信息重疊程度較高，可用因子分析模型進(jìn)行降維[20]．檢驗樣本分布的Barlett近似卡方值600.805，顯著性水平=0.000<0.05，說明拒絕各變量獨立的假設(shè)，即變量間有較強(qiáng)的相關(guān)關(guān)系，在5%的顯著性水平下，測試數(shù)據(jù)適合進(jìn)行因子分析．

其次，選擇主成分法和旋轉(zhuǎn)方法進(jìn)行因素分析．用SPSS軟件得到表5．

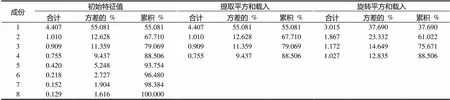
表5 解釋的總方差

一般情況下，累計方差貢獻(xiàn)率應(yīng)達(dá)到85%以上，才能說明選取的因子基本包含全部指標(biāo)的信息．這里，提取4個主成分時，解釋率為88.506%，故選取4個主成分．進(jìn)一步用SPSS軟件分析，得到旋轉(zhuǎn)成份矩陣，如表6所示．

表6 旋轉(zhuǎn)成份矩陣a

可見，4個主成分中，成分1與觀察、比較、分類、歸納的載荷較大；成分2與類比、聯(lián)想的載荷較大；成分3與數(shù)學(xué)表達(dá)的載荷較大；成分4與證明的載荷較大．

3.4 基于聚類分析的數(shù)學(xué)基本活動經(jīng)驗層次水平劃分

下面根據(jù)學(xué)生的得分對學(xué)生進(jìn)行聚類．將每個學(xué)生的總分、4個主成分的各自得分共5個數(shù)據(jù)作為聚類指標(biāo)，進(jìn)行分層聚類．利用SAS統(tǒng)計軟件進(jìn)行分析，得到的結(jié)果如表7．

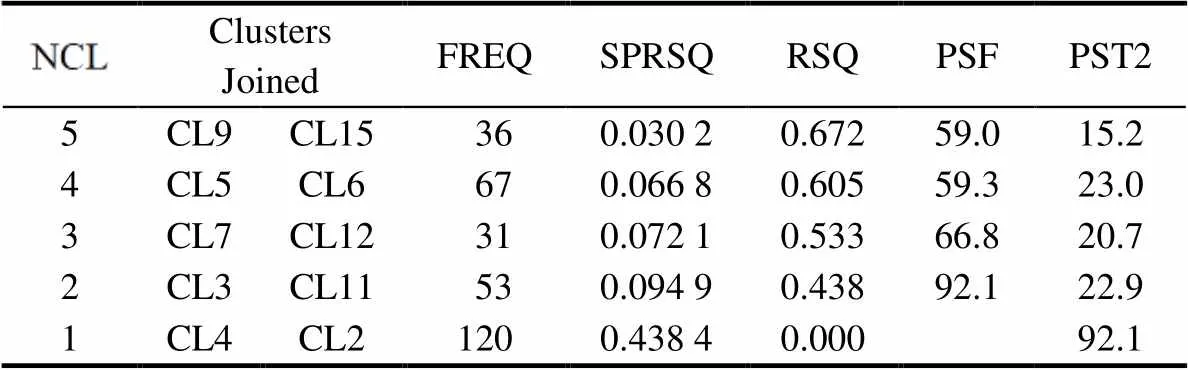
表7 聚類表

表8 聚類結(jié)果

4 結(jié)論與討論

4.1 研究結(jié)論

4.1.1 數(shù)學(xué)基本活動經(jīng)驗的主成分和各主成分的要素構(gòu)成

研究只針對數(shù)學(xué)思維活動的經(jīng)驗．在分析數(shù)學(xué)家進(jìn)行數(shù)學(xué)創(chuàng)造的過程和中學(xué)一線數(shù)學(xué)教師調(diào)研基礎(chǔ)上，給出數(shù)學(xué)基本活動經(jīng)驗的8個成分研究假設(shè)，分別是觀察、比較、分類、歸納、類比、聯(lián)想、數(shù)學(xué)表達(dá)、證明．主成分分析顯示，成分1與觀察、比較、分類、歸納的載荷較大，命名成分1為歸納概括；成分2與類比、聯(lián)想的載荷較大，命名成分2為類比推廣；成分3與數(shù)學(xué)表達(dá)的載荷較大，命名成分3為數(shù)學(xué)表達(dá)；成分4與證明的載荷較大，命名成分4為證明．各成分的要素構(gòu)成如下．

歸納概括是在觀察的基礎(chǔ)上對事物進(jìn)行比較，進(jìn)而將事物分類并由每類事物的特殊屬性歸納其一般屬性．其中，數(shù)學(xué)觀察是對事物共性、特性、關(guān)系進(jìn)行分析的過程；比較是確定研究對象的相同點和不同點；分類是根據(jù)研究對象的性質(zhì)、找到合適的分類標(biāo)準(zhǔn)進(jìn)而劃歸為不同類別；歸納是通過一類事物的部分對象具有某種屬性，推知該類事物都具有這一屬性．在觀察、比較、分類和歸納基礎(chǔ)上可以提出數(shù)學(xué)猜想．

類比推廣是根據(jù)某類事物的屬性而猜測在其它類的事物也可能存在相同或相似之處，進(jìn)而引發(fā)思考并做相應(yīng)的推廣．歸納、類比、聯(lián)想往往是有機(jī)結(jié)合在一起，但類比與歸納相比，需要更豐富的聯(lián)想．

前兩個成分主要是提出數(shù)學(xué)猜想，數(shù)學(xué)表達(dá)是用符號等數(shù)學(xué)語言表達(dá)數(shù)學(xué)猜想或其它結(jié)論．

數(shù)學(xué)猜想的結(jié)果是否成立需要借助數(shù)學(xué)證明．?dāng)?shù)學(xué)證明保證了由歸納或類比得到的一般命題的普遍有效性，是由命題的條件出發(fā)，根據(jù)與此相關(guān)的定義、公理、定理等，按照邏輯推理規(guī)則進(jìn)行的邏輯推演．

這4個主成分反映數(shù)學(xué)思維活動的過程，是數(shù)學(xué)基本活動經(jīng)驗的因素構(gòu)成．

4.1.2 數(shù)學(xué)基本活動經(jīng)驗的層次水平劃分

聚類結(jié)果表明，數(shù)學(xué)基本活動經(jīng)驗的每個主成分都對應(yīng)了3類學(xué)生，即每個主成分可以劃分為3個層次．以下從每個類別中挑取個案來說明各層次特點：

關(guān)于歸納概括，學(xué)生得分由高到低依次為類別3、類別2、類別1，每個類別分別對應(yīng)了歸納概括的層次1、層次2、層次3．每個層次學(xué)生的特點如表9．

表9 主成分1的不同層次特點

如測試題的第9題．該題的目的是：考察學(xué)生能否由特殊歸納一般，參考了波利亞《數(shù)學(xué)鍛煉大腦——斯坦福大學(xué)數(shù)學(xué)試題與解答》．

原題為：如圖2所示，第一層是一條與水平線垂直的線段，長度為1；第二層是在第一層的前端作2條與該線段成135°角的線段，長度為其一半；第三層按第二層的方法在每一線段的前端生成兩條線段，長度為第二層的一半；重復(fù)前面的做法作圖至第層．該樹的第層的最高點至水平線的距離為第層的樹形的高度．問：第層的高度是多少？請寫出詳細(xì)的計算過程．

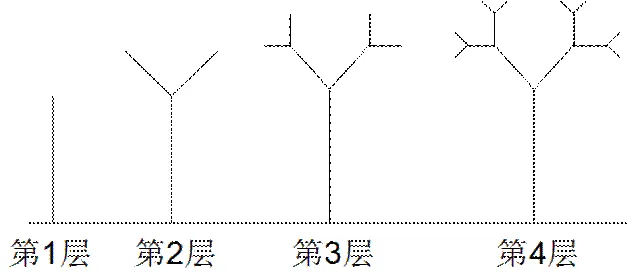
圖2 測試題第9題圖示

不同層次的學(xué)生對這道題有不同的解答．層次1的學(xué)生寫出了第2、3層的高度，并且對進(jìn)行分類，總結(jié)出了第層的高度；層次2的學(xué)生寫出了第2、3層的高度，沒有寫出第層的高度；層次3的學(xué)生的答卷空白，他們表示對于這道題不知道如何下手，不知從特殊出發(fā)歸納一般．

關(guān)于類比推廣，學(xué)生得分由高到低依次為類別3、類別1、類別2，每個類別分別對應(yīng)了類比推廣的層次1、層次2、層次3．每個層次學(xué)生的特點如表10．

表10 主成分2的不同層次特點

如測試題的第11題．該題的目的是：考察學(xué)生是否會類比猜想，即能否將等比數(shù)列中成立的結(jié)論類比到等差數(shù)列中，參考的是2013浙江鎮(zhèn)海中學(xué)3月模擬卷的第17題．

不同層次的學(xué)生的答題情況不同．層次1和層次2的學(xué)生都知道等比類比到等差，積類比到和，商類比到差，層次1的學(xué)生寫出的結(jié)果為，他們知道類比到等差，積類比到和，商類比到差．層次2的學(xué)生得出的結(jié)果是錯誤的，他們知道等比類比到等差，積類比到和，商類比到差，但是他們無法對類比后的結(jié)論進(jìn)行調(diào)整；層次3的學(xué)生的答卷空白，他們不知道等比類比到等差，積類比到和，商類比到差，不能找到合適的類比對象．

關(guān)于數(shù)學(xué)表達(dá)，學(xué)生得分由高到低依次為類別3、類別2、類別1，每個類別分別對應(yīng)了數(shù)學(xué)表達(dá)的層次1、層次2、層次3．每個層次學(xué)生的特點如表11．

表11 主成分3的不同層次特點

如測試題中的第17題．該題的目的是：考察學(xué)生能否會用符號語言進(jìn)行數(shù)學(xué)表達(dá)，參考人民教育出版社A版數(shù)學(xué)必修教材．

原題為：將其轉(zhuǎn)換成符號語言：一條直線與一個平面內(nèi)的兩條相交直線都垂直，則該直線與此平面垂直．

層次1的學(xué)生給出了正確答案，他們表示這道題十分簡單；層次2的學(xué)生在進(jìn)行數(shù)學(xué)表達(dá)時會漏掉題目中的關(guān)鍵信息，如“直線不在平面內(nèi)”這個關(guān)鍵信息漏掉；層次3的學(xué)生不會用數(shù)學(xué)符號進(jìn)行表達(dá)．

關(guān)于證明，學(xué)生得分由高到低依次為類別3、類別1、類別2，每個類別分別對應(yīng)了證明的層次1、層次2、層次3．每個層次學(xué)生的特點如表12．

表12 主成分4的不同層次特點

如測試題中的第18題．該題改編自2013年北京高考理科數(shù)學(xué)卷的第19題，這道題要求學(xué)生先判斷四邊形的形狀，再給出證明．其本質(zhì)是一道證明題，因為學(xué)生很容易判斷出不是菱形，進(jìn)而此題就轉(zhuǎn)化成了證明不是菱形，是一道證明題，其目的是：考察學(xué)生是否會進(jìn)行演繹證明．

原題為：已知、、是橢圓上上的3個點，是坐標(biāo)原點．若點不是的頂點時，四邊形是否可能為菱形，說明理由．

不同層次的學(xué)生的答題情況不同．層次1的學(xué)生所用的方法合理，知道用反證法證明，證明過程都是對的，邏輯性強(qiáng)，思路清晰．層次2的學(xué)生知道用反證法進(jìn)行證明，但是并沒有得出最終結(jié)果．層次3的學(xué)生表示對于這樣的題目無從下手．

4.2 討 論

4.2.1 明確數(shù)學(xué)課程實施和教學(xué)實踐中的關(guān)鍵環(huán)節(jié)

研究給出了數(shù)學(xué)基本活動經(jīng)驗的主成分：歸納概括、類比推廣、數(shù)學(xué)表達(dá)、證明．這幾個成分是學(xué)生數(shù)學(xué)創(chuàng)新能力培養(yǎng)的關(guān)鍵，是數(shù)學(xué)基本活動經(jīng)驗的4個關(guān)鍵因素．它們勾勒出了人們進(jìn)行數(shù)學(xué)思維、包括數(shù)學(xué)的產(chǎn)生與發(fā)展過程中的關(guān)鍵環(huán)節(jié)，反映了科學(xué)的思考問題的方式．因而，有關(guān)數(shù)學(xué)基本活動經(jīng)驗主成分的定量分析，進(jìn)一步明確了義務(wù)教育數(shù)學(xué)課程目標(biāo)中提出的數(shù)學(xué)基本活動經(jīng)驗的構(gòu)成要素，對于指導(dǎo)一線教師在實踐教學(xué)中落實數(shù)學(xué)基本活動經(jīng)驗的課程目標(biāo)提供了方向性指導(dǎo)．

數(shù)學(xué)教學(xué)中應(yīng)該過程教學(xué)和結(jié)果教學(xué)相結(jié)合，然而，什么是過程教學(xué)？過程教學(xué)的結(jié)果是什么？對此是缺乏深入的理論探討的．借助主成分分析，在研究假設(shè)基礎(chǔ)上確定的數(shù)學(xué)基本活動經(jīng)驗的主成分，說明了數(shù)學(xué)過程教學(xué)的4個關(guān)鍵環(huán)節(jié)，同時，數(shù)學(xué)過程教學(xué)的結(jié)果之一是積累學(xué)生數(shù)學(xué)思考問題的方式或習(xí)慣，這是長期經(jīng)歷這4個關(guān)鍵環(huán)節(jié)后的結(jié)果．

4.2.2 明確數(shù)學(xué)基本活動經(jīng)驗各環(huán)節(jié)的不同層次水平

這里將數(shù)學(xué)基本經(jīng)驗的每個環(huán)節(jié)都劃分成3個層次，每個層次的學(xué)生具有不同的特點，也代表了每個環(huán)節(jié)發(fā)展過程中所處的不同階段．借助聚類分析得到的學(xué)生數(shù)學(xué)基本活動經(jīng)驗4個主成分的不同層次水平，可以幫助教師了解不同層次水平學(xué)生的表現(xiàn)和特征，有針對性地實施區(qū)別化教學(xué)，對于大面積提高數(shù)學(xué)教學(xué)質(zhì)量也將是一個有益的啟示．

4.2.3 推動學(xué)生數(shù)學(xué)核心素養(yǎng)研究的進(jìn)展

盡管目前國內(nèi)外對“何為數(shù)學(xué)素養(yǎng)”并沒有統(tǒng)一的認(rèn)識，關(guān)于數(shù)學(xué)核心素養(yǎng)的幾個方面：抽象、推理、建模，以及運算、思維、空間想象等數(shù)學(xué)素養(yǎng)的具體內(nèi)涵、構(gòu)成要素等仍在研究、討論中[21]．但是，比較一致的看法是數(shù)學(xué)學(xué)科核心素養(yǎng)的養(yǎng)成需要學(xué)生的知識儲備、能力發(fā)展、經(jīng)驗積累．積累數(shù)學(xué)基本活動經(jīng)驗是數(shù)學(xué)素養(yǎng)養(yǎng)成的一個方面，對數(shù)學(xué)基本活動經(jīng)驗的主成分和層次水平的研究，進(jìn)一步明確了從哪些關(guān)鍵方面積累學(xué)生數(shù)學(xué)基本活動經(jīng)驗，在這些關(guān)鍵方面學(xué)生的不同層次劃分如何，這對研究數(shù)學(xué)核心素養(yǎng)，推動學(xué)生數(shù)學(xué)核心素養(yǎng)的養(yǎng)成無疑將起到巨大的推動作用．

[1] 中華人民共和國教育部．《教育部關(guān)于全面深化課程改革落實立德樹人根本任務(wù)的意見》（教基二[2014]4號）[EB/OL]．http://www.moe.edu.cn/publicfiles/business/htmlfiles/moe/s7054/201404/167226.html

[2] 喻平．?dāng)?shù)學(xué)學(xué)科核心素養(yǎng)要素析取的實證研究[J]．?dāng)?shù)學(xué)教育學(xué)報，2016，25（6）：1-6．

[3] 鄭毓信．?dāng)?shù)學(xué)教育視角下的“核心素養(yǎng)”[J]．?dāng)?shù)學(xué)教育學(xué)報，2016，25（3）：1-5．

[4] 何小亞．學(xué)生“數(shù)學(xué)素養(yǎng)”指標(biāo)的理論分析[J]．?dāng)?shù)學(xué)教育學(xué)報，2015，24（1）：13-19．

[5] 顧繼玲．聚焦“基本數(shù)學(xué)活動經(jīng)驗”[J]．?dāng)?shù)學(xué)教育學(xué)報，2016，25（1）：34-37．

[6] 王新民，王富英，王亞熊．?dāng)?shù)學(xué)“四基”中“基本活動經(jīng)驗”的認(rèn)識與思考[J]．?dāng)?shù)學(xué)教育學(xué)報，2008，17（3）：17-20．

[7] 宋運明．論數(shù)學(xué)問題提出和數(shù)學(xué)活動經(jīng)驗的關(guān)系[J]．?dāng)?shù)學(xué)教育學(xué)報，2010，19（6）：34-36，49．

[8] 張奠宙，竺仕芬，林永偉．“基本活動經(jīng)驗”的界定與分類[J]．?dāng)?shù)學(xué)通報，2008，（5）：4-7．

[9] 仲秀英．促進(jìn)學(xué)生積累數(shù)學(xué)活動經(jīng)驗的教學(xué)策略[J]．?dāng)?shù)學(xué)教育學(xué)報，2010，19（5）：36-39．

[10] 徐章韜．超級畫板：獲取數(shù)學(xué)基本活動經(jīng)驗的優(yōu)秀認(rèn)知平臺[J]．?dāng)?shù)學(xué)教育學(xué)報，2011，20（3）：97-99．

[11] 郭玉峰，史寧中．?dāng)?shù)學(xué)基本活動經(jīng)驗：提出、理解與實踐[J]．中國教育學(xué)刊，2012，（4）：42-45．

[12] 郭玉峰，史寧中．“數(shù)學(xué)基本活動經(jīng)驗”研究：內(nèi)涵與維度劃分[J]．教育學(xué)報，2012，（5）：23-28．

[13] 郭玉峰，史寧中．初中學(xué)生基本數(shù)學(xué)活動經(jīng)驗的量化研究[J]．課程·教材·教法，2013，（11）：48-54．

[14] 克魯捷茨基．中小學(xué)數(shù)學(xué)能力心理學(xué)[M]．上海：上海教育出版社，1987．

[15] 李洪玉，林崇德．中學(xué)生空間認(rèn)知能力結(jié)構(gòu)的研究[J]．心理科學(xué)，2005，（2）：269-271．

[16] 郭玉英．物理思維能力的因子分析模型及主因素研究[J]．北京師范大學(xué)學(xué)報（自然科學(xué)版），1988，（4）：107-111．

[17] 雅克·阿達(dá)瑪．?dāng)?shù)學(xué)領(lǐng)域中的發(fā)明心理學(xué)[M]．大連：大連理工大學(xué)出版社，2008．

[18] 衷克定．SPSS for windows數(shù)據(jù)統(tǒng)計分析工具應(yīng)用教程[M]．北京：北京師范大學(xué)出版社，2001．

[19] 高惠璇．實用統(tǒng)計方法與SAS系統(tǒng)[M]．北京：北京大學(xué)出版社，2001．

[20] 張紅坡．SPSS統(tǒng)計分析實用寶典[M]．北京：清華大學(xué)出版社，2012．

[21] 周彥池，裴昌根．?dāng)?shù)學(xué)教育研究與實踐的熱點及趨勢[J]．?dāng)?shù)學(xué)教育學(xué)報，2016，25（6）：93-95．

[責(zé)任編校：周學(xué)智]

Research on the Principal Component and Hierarchical Level Division of the Mathematical Activity Experience

GUO Yu-feng1, ZHANG Fang1, 2

(1. School of Mathematical Science, Beijing Normal University, Beijing 100875, China;2. The Affiliated High School of Zhejiang University, Zhejiang Hangzhou 310000, China)

The article investigated the integrant parts of students’ mathematical activity experience based on literature analysis and investigation. By factor analysis, four principle components were determined which were inductive generalization, analogy extension, mathematical expression, mathematical prove. By cluster analysis, hierarchical level diversion of mathematical activity experience were also determined. The research would prompt the implantations of curriculum objectives and core competences of mathematics.

mathematical activity experience; principal component; hierarchical level division

G420

A

1004–9894（2017）03–0025–05

2017–02–08

北京市教育科學(xué)“十二五”規(guī)劃重點課題——“四基”之?dāng)?shù)學(xué)基本活動經(jīng)驗研究：量化與課堂實踐（ABA12020）

郭玉峰（1972—），女，山東日照人，教授，博士生導(dǎo)師，主要從事數(shù)學(xué)課程與教材、數(shù)學(xué)學(xué)習(xí)心理研究．