加速運動點電荷瞬時自身系中的勢與場

楊煥雄

(中國科學技術大學近代物理系，安徽 合肥 230026)

?

加速運動點電荷瞬時自身系中的勢與場

楊煥雄

(中國科學技術大學近代物理系，安徽 合肥 230026)

本文從點電荷在自身系中激發的惠特克(Whittaker)勢出發，通過點電荷自身參考系與瞬時自身系之間的廣義林德勒(Rindler)變換分析了點電荷做一般加速運動時其瞬時自身系中的電磁勢與場強分布。使用四維張量在不同參考系變換的方法所求出的點電荷在瞬時自身系中的電場強度分布與前人通過定性分析得出的結果一致。本文的新意在于求出了點電荷瞬時自身系中的電磁勢具有非零的空間分量，從而消除了流行教材在此問題上潛在的邏輯漏洞。本文的工作或許可以為使用洛倫茲變換推求運動點電荷在一般的慣性參考系中激發的電磁場分布的方法提供一個可靠的物理前提。

瞬時自身系;自身系;廣義林德勒變換;惠特克勢

經典電動力學的一個著名結論是：相對于慣性參考系的觀測者而言，做加速運動的帶電粒子會激發輻射電磁場。這一論斷不僅提供了實驗室里通過人工方式產生電磁波的物理基礎，它在歷史上也對原子的盧瑟福行星模型進化到玻爾模型，進而對于海森堡建立量子力學的矩陣力學表述起到過積極的推動作用。在慣性參考系中計算運動點電荷(可以不是作勻速直線運動)激發的電磁場強，常見的策略是首先求出相應的推遲電磁勢、 即李納-魏謝爾勢[1-3]。推導李納-魏謝爾電磁勢的一種有趣的方法是構建運動點電荷的瞬時自身系。特別地，在國內流行的、由郭碩鴻等教授所著的電動力學教材中，點電荷激發的電磁勢在瞬時自身系里被先驗地假設為純粹的庫侖靜電標勢[1]。注意到電磁勢形成四維閔可夫斯基空間中的矢量，且電磁勢只與點電荷的運動速度有關[1,2]，可以通過洛倫茲變換求出此運動點電荷在實驗室參考系中激發的李納-魏謝爾勢。再計算李納-魏謝爾勢對于時間參數及空間坐標的微商，就可求得帶電粒子所激發的電磁場強。

把點電荷瞬時自身系中的電磁勢假設為庫侖靜電標勢貌似當然，其實在物理邏輯上是說不通的。我們知道：對于任一慣性參考系中的觀測者而言，點電荷做加速運動時會激發輻射電磁場[1-3]。所以，點電荷激發的電磁場在其瞬時自身系中表現為庫侖場與粒子加速度相關的輻射場的矢量疊加是經典電動力學理論無可辯駁的結論。倘若電磁勢在瞬時自身系中僅僅具有非零的標勢(例如文獻[1]中假設的庫侖勢，或者李納-魏謝爾勢在粒子速度趨于零情形下的極限)，但矢勢為零，則此點電荷激發的電磁場在瞬時自身系中只能表現為純電場，不可能支撐非零的輻射電磁場能流密度。這一邏輯缺陷顯然不能通過電磁勢的規范變換得以挽救。

筆者在電動力學的教學過程中還曾遇到某些同學提問到另一個相關的、有趣的問題： 可否直接從瞬時自身系中點電荷的電磁場出發、 通過洛倫茲變換求得實驗室參考系里電磁場的場強?電磁場強構成四維閔可夫斯基空間中的二階反對稱張量，其在不同慣性系中的分量自然應通過洛倫茲變換相聯系。洛倫茲變換是張量分量間的線性關系，變換式本身只依賴于兩個慣性系之間的相對速度。倘若假設點電荷激發的電磁場在其瞬時自身系中表現為純粹的庫侖靜電場(這可能是一般人的直覺)，則通過洛倫茲變換求得的實驗室參考系中的“電磁場”將僅僅依賴于點電荷相對于實驗室系的速度。這個結果顯然是荒謬的。眾所周知，點電荷做加速運動時其激發的電磁場強是與加速度相關的。通過求李納-魏謝爾推遲勢的時空導數得到的電磁場強度中就含有點電荷的加速度。試圖直接通過場強的洛倫茲變換求得實驗室系中電磁場的思路在邏輯上并沒有錯，事實上確有按照這一思路成功地求出了加速帶電粒子激發的輻射電磁場的先例[4,5]。問題的要害仍然在于：點電荷激發的電磁場在其瞬時自身系中并不表現為純粹的庫侖靜電場[6,7]。

一個回避上述邏輯困難的策略是放棄瞬時自身系的概念，在確定做加速運動的點電荷所激發的電磁勢和電磁場問題上拒絕使用洛倫茲變換。某些電動力學教材或者參考書的作者通過含時格林函數方法[2,3,8]，直接在實驗室參考系中求出了李納-魏謝爾推遲勢，再進行若干矢量分析運算就求出了相應的場強分布。這一方案確無邏輯漏洞，但放棄了優美的參考系變換方法難免讓人感到惋惜。本文試圖在同一問題上重拾參考系變換的方法，需要面對的核心困難是如何合理地確定瞬時自身系中的電磁勢和場強分布。點電荷做加速運動情形下，任一時刻與其保持相對靜止的參考系實際上有兩個，即自身系與瞬時自身系。瞬時自身系是慣性參考系，但自身系卻不然。因為點電荷在自身系中自始至終處于靜止狀態，點電荷相對于慣性系做加速運動時其自身系無疑是非慣性參考系。本文擬在點電荷的自身系中求解麥克斯韋方程組，求出自身系中的電磁勢和電磁場。然后通過自身系與瞬時自身系之間的參考系變換求得點電荷瞬時自身系中電磁勢和場強分布，為進一步使用洛倫茲變換確定實驗室參考系中的電磁勢和電磁場奠定邏輯上可靠的出發點。

1 自身系與瞬時自身系

(1.1)

線元ds2是閔可夫斯基空間中的標量，

(1.2)

(1.3)

而

(1.4)

是聯絡系數。把式(1.1)代入到零曲率條件中，不難看到g00(x,t)的解在物理上是唯一的[8]：

(1.5)

式中參量g(t)是時間參數t的任意函數，其物理意義待定。把(1.5)代回到式(1.2)，四維閔可夫斯基空間中線元的不變性可以重新寫為

(1.6)

(1.7)

(1.8)

加速參考系S中的坐標系相對于S系觀測者而言仍是剛性坐標系[10]，V只依賴于時間參數t。由此知：ξ=ξ(t)。如圖1所示，變換式(1.7)只能覆蓋閔可夫斯基空間中的部分區域。進一步分析S系中具有確定坐標值x的質點的測地線方程，可以證明[9]：

(1.9)

圖1 加速度a(τ)取常數值a時質點做勻加速直線運動，此時變換式(1.7)在閔可夫斯基空間中覆蓋的區域位于圖上兩條虛線之間。雙曲線是質點在瞬時自身系中的運動方程：(1+aX)2-(aT)2=1

(1.10)

以下約定V0=0。在g(t)=a為常數的情形下，微分形式的變換式(1.7)退化為全微分。積分之，可得

(1.11)

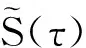
(1.12)

姑且稱式(1.12)為廣義林德勒變換。由此知閔可夫斯基空間中四維張量的坐標變換矩陣和逆矩陣分別為

(1.13)

與

(1.14)

(1.13)及(1.14)式中引入了新參量：ζ=a(τ)(t-t0)。閔可夫斯基空間中的線元可以在S系中重新表為

(1.15)

2 加速運動點電荷自身系中的電磁場

本節考慮做加速運動的點電荷在自身參考系中激發的電磁場。假設點電荷q在自身參考系S中的位置矢量為r0=(0,0,0)。協變形式的麥克斯韋方程組可寫為

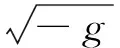
(2.1)

Fμ ν=gμ αgν βFα β，

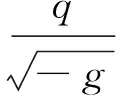
(2.2)

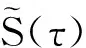
(2.3)

所以，

(2.4)

結合式(2.2)、(2.4)與(2.1)，可知標勢A0服從如下微分方程：

(2.5)

(2.6)

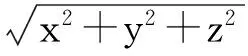
模仿慣性參考系中場強矢量E,B與電磁場張量Fμ ν的關系，我們在q自身系S里定義：

Ei=F0i,Bi=-εijkFjk

(2.7)

顯然，E=-A0且B=0。代入惠特克勢A0的具體形式(2.6)，不難求得：

(2.8)

不同于靜止于慣性參考系中的點電荷所產生的靜電庫侖場，式(2.8)描寫的電場強度分布沒有球對稱性，不遵守平方反比律且通過點電荷的加速度a(τ)依賴于時間。不過，鑒于坡印廷矢量S∝E×B=0，做加速運動的點電荷q在其自身系中并不激發電磁輻射。

3 瞬時自身系中的電磁勢與場強

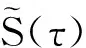
電磁勢形成四維閔可夫斯基空間中的矢量，

(3.1)

電磁場的場強形成閔可夫斯基空間中的二階反對稱張量，

(3.4)

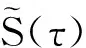
作為對于(3.5)～(3.10)諸式正確性的一種交叉檢驗，我們也可以直接使用場強與勢之間的關系

(3.11)

比較知兩種方法求得的場強分布完全一致。

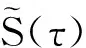
(3.12)

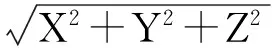
利用這些輔助公式改寫式(3.2)與式(3.3)，我們有：

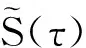
(3.15)

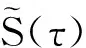
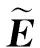
(3.16)

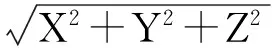
(3.17)

這是q的自身系S完全不具備的性質。

4 結語

本文討論了點電荷做加速運動時其瞬時自身系中的電磁勢與場強分布。在點電荷做一般加速運動的情形下，我們分析了點電荷自身參考系與瞬時自身系之間的物理差異并討論了它們之間的坐標變換(廣義林德勒變換)。根據點電荷在自身系中激發的惠特克勢，我們使用閔可夫斯基空間中張量的變換法則求出了當點電荷做一般加速運動時其瞬時自身系中的電磁勢與場強分布。通過參考系變換方式求出的點電荷在瞬時自身系中的電場強度分布與前人通過定性分析得出的結果一致。本文的新意在于強調指出了點電荷瞬時自身系中的電磁勢具有非零的空間分量，這個結論消除了流行教材在此問題上的可能存在的邏輯障礙，為進一步使用洛倫茲變換獲得一般實驗室參考系中的電磁勢和電磁場分布提供了可靠的物理基礎。此外，本文的工作或許可以看作文獻[15]中古普塔(Gupta)等人所討論的點電荷做勻加速直線運動情形下的同類工作向點電荷做一般加速運動情形的推廣。

筆者感謝第16屆全國電動力學研討會上李志兵、王振林、曾定方、鄭漢青、周磊和朱全界等教授給予的批評與建議，也感謝在中國科學技術大學2015—2016年電動力學教學過程中就相關問題與閔皓彥、董伊云和郝云超等同學的討論。

[1] 郭碩鴻，黃迺本,李志兵,等.電動力學[M].北京：高等教育出版社，2008.

[2] Jackson J.D. Classical Electrodynamics[M]. Wiley, 1998.

[3] Zangwill A. Modern Electrodynamics[M]. CUP, 2012.

[4] 虞炎華，張雨風.四維協變式與高能帶電粒子的電磁場[J].大學物理，1990,26(7):8. Yu Yanhua, Zhang Yufeng. Four-dimensional Covariant Formalism and the Electromagnetic Fields of a charged particle[J]. College Physics, 1990, 26(7): 8. (in Chinese)

[5] Padmanabhan H . A simple derivation of the electromagnetic field of an arbitrarily moving charge[J]. Am .J.Phys., 2009, 77, 151.

[6] Padmanabhan T. Theoretical Astrophysics: Astrophysical Processes, Vol.1[M]. CUP, 2000.

[7] 趙凱華，陳熙謀.新概念物理教程：電磁學[M].北京：高等教育出版社，2003.

[8] 胡友秋，程福臻.電磁學與電動力學，下冊[M].北京：科學出版社，2014.

[9] Deng J B, Hu X R, Ding Y M, et al. On General Moller Transformation[J]. Commun. Theor. Phys., 2009, 52: 75.

[10] Landau L, Lifshitz E. The Classical Theory of Fields[M]. Butterworth-Heinemann, 1975.

[11] Ryder L. Introduction to General Relativity[M]. CUP, 2009.

[12] Moller C. The Theory of Relativity[M]. Clarendon, Oxford, 1952.

[13] Rindler W. Hyperbolic Motion in Curved Space-Time[J]. Phys. Rev. 1960, 119: 2082.

[14] Whittaker E T. On Electric Phenomena in Gravitational Fields[J]. Proc. R. Soc. A, 1927, 116: 720.

[15] Gupta A, Padmanabhan T. Radiation from a charged particle and radiation reaction reexamined[J]. Phys. Rev. D, 1998, 57: 7241.

■

THE POTENTIALS AND FIELDS OF AN ACCELERATED CHARGE IN ITS INSTANTANEOUS REST FRAME

Yang Huanxiong

(Department of Modern Physics, University of Science and Technology of China, Hefei Anhui 230026)

Starting from the Whittaker potential of an accelerated point charge in its comoving frame, we discuss the calculations of electromagnetic potentials and field strengths of the charge in the inertial frame in which the charge keeps static instantaneously. Our strategy is to utilize a generalized Rindler transformation between the mentioned two frames, and our results on field strengths coincide with those derived from Green function methods or Lienard-Wiechert potential. What is new of the paper relies on the fact that we have found a nonvanishing spatial component of the potential 4-vector in the instantaneously comoving frame, that eliminates a possible bug of Lienard-Wiechert potential. Our work does probably supply a solid starting point for utilizing Lorentz transformations to calculate the potential and field strength of a charged particle in general inertial frames.

instantaneous rest frames; comoving frame; generalized Rindler transformation; Whittaker potential

2016-12-31

楊煥雄，男，副教授，主要從事電動力學教學工作，科研方向為超弦宇宙學。hyang@ustc.edu.cn

楊煥雄. 加速運動點電荷瞬時自身系中的勢與場[J]. 物理與工程，2017，27(3)：84-90.