Mathematica在普通物理教學中的應用

劉 鑫 趙里昂 于文晶 楊華哲

(中國醫科大學公共基礎學院物理與生物物理教研室, 遼寧 沈陽 110122)

Mathematica在普通物理教學中的應用

劉 鑫 趙里昂 于文晶 楊華哲

(中國醫科大學公共基礎學院物理與生物物理教研室, 遼寧 沈陽 110122)

目的：針對高校普通物理的傳統課堂教學內容抽象復雜，教學方式較大局限性及學生吸收知識慢、興趣弱等問題，可適當引入計算機軟件支撐教學，豐富課堂，解決以上教學難題。方法：運用Mathematica軟件的強大動畫和繪圖功能，對普通物理教學中振動和波的幾個典型問題進行分析。結果：通過將教學軟件Mathematica與基礎物理知識的講授教學有機結合，可以將課堂中原始化手工推算的內容直觀圖像化、動畫化，令學生更直觀地理解課堂內容。結論：通過對實例的闡述可以看出，將Mathematica引入教學能夠幫助學生更快、更好地理解物理知識，同時激發學生對物理知識的濃厚興趣，培養學生的獨立思考能力，使課堂教學更高效。

Mathematica；普通物理；教學模式

在普通物理知識的教學過程中, 包含力學、熱學、光學、電磁學等課程. 其中不乏些復雜抽象的物理問題, 原始課堂教學雖有多媒體課件等教學手段, 依然無法避免應用手工推算的方法讓學生理解物理規律, 在這種枯燥的教學模式下, 學生即使可以得到解析結果, 卻不易得到直觀的物理圖像, 很大程度抑制了學生的學習興趣. 與此同時, 由于課堂教學的時間局限性, 需要學生在很短的時間內快速對較多的抽象理論進行推算和深入理解, 并完成許多基于高等數學的高等運算,已經成為高校普通物理的教學瓶頸。為了解決上述問題, 國內許多高校開始引入教學軟件來豐富學生對普通物理知識的直觀理解, 目前Matlab、Maple、 Mathematica、MathCAD等幾大數學軟件工具可以有效地與理論知識教學相結合, 達到較好的課堂教學效果。其中Mathematica作為一個著名的數學軟件, 相對其他教學軟件更加小巧方便。Mathematica主要是由美國Wolfram公司研究開發, 可用來從事數值、符號的相關運算,擁有從多項式運算到微積分、特殊函數分析運算等豐富的功能。與Matlab等軟件相比, Mathematica在無需掌握C語言或Fortran等復雜計算機語言條件下即可滿足物理教學中對完成數學圖形繪制，甚至動畫制作等多種需求，避免了漫長的熟練計算機語言過程。此外，Mathematica在一個notebook里面即可把公式文檔和計算過程一一表達, 擁有簡單語法卻可實現強大功能, 這在此類軟件中非常難得。因此, 如將Mathematica適當地引入普通物理的教學, 在進行簡單的學習教程后就可編程出需要的教學內容, 即可將原本復雜的原始化手工推算用Mathematica作圖來給學生以直觀展示, 也可快速編譯出抽象物理理論的動畫來推進課程進行, 激發學生對原本枯燥復雜的物理規律的學習興趣, 這樣既可以節省課堂時間來進行原本的手工推算, 又會使學生快速吸收普通物理的理論知識, 提高課堂授課效率。通過借助此類計算軟件實現物理理論的可視化教學，對于探索新型的高效課堂教學具有重要的意義。

1 應用舉例

普通物理中涉及許多知識, 此處針對機械運動和機械波部分進行舉例。與一些物理理論相似, 振動和波經常涉及復雜的數學運算, 因此可在教學中引入Mathematica繪制出生動精美的波形與動畫, 豐富課堂教學, 可以起到事半功倍的效果。

1.1 振動的合成圖形

由于振動的合成多種多樣, 書本和手工演算很難為學生建立形象、直觀的物理模型，影響了學生對于知識的理解。由于Mathematica軟件有強大的動態圖形演示功能, 所以在教學過程中, 適當穿插動態圖形演示很必要。

1.1.1 兩個同方向同頻率的簡諧振動的合成圖像

兩個同方向同頻率的簡諧振動合成之后仍為簡諧振動, 頻率不變。令兩個分振動分別為y1=A1cosωt和y2=A2cos(ωt+2πφ), 合振動則是二者之和, 其中ω=1rad·s-1,筆者在軟件中將φ取值范圍定義在0到1之間, 可在軟件運行過程中改變數值觀察圖像, 分振動的振幅A1可取值為1、2, 振幅A2可取值為0、1、2, 然后將3條簡諧振動的曲線在同一坐標中體現。

運行命令如下

Manipulate[Plot[{A1 Cos[t], A2 Cos[t+2 Pi phi], A1 Cos[t]+A2 Cos[t+2 Pi phi]}, {t, 0, 4 Pi}, Frame -> True, PlotRange -> 4, PlotStyle -> {Dashed, Green, Blue}, PlotLegends -> {"SBM1", "SBM2", "SBM1+SBM2"}],{phi, 0, 1}, {A1, {1, 2}}, {A2, {0, 1, 2}}]

運行后可以在統一坐標中得到3條簡諧振動的曲線, 并可以通過改變各分振動的振幅, 得到對應的簡諧振動圖像, 圖1展示了程序通過改變振幅值而得到的瞬時簡諧振動圖像。圖2展示了程序通過改變某分振動φ的取值范圍定義所得到的瞬時簡諧振動圖像.

1.1.2 兩個方向垂直的簡諧振動的合成圖像——李薩茹圖形

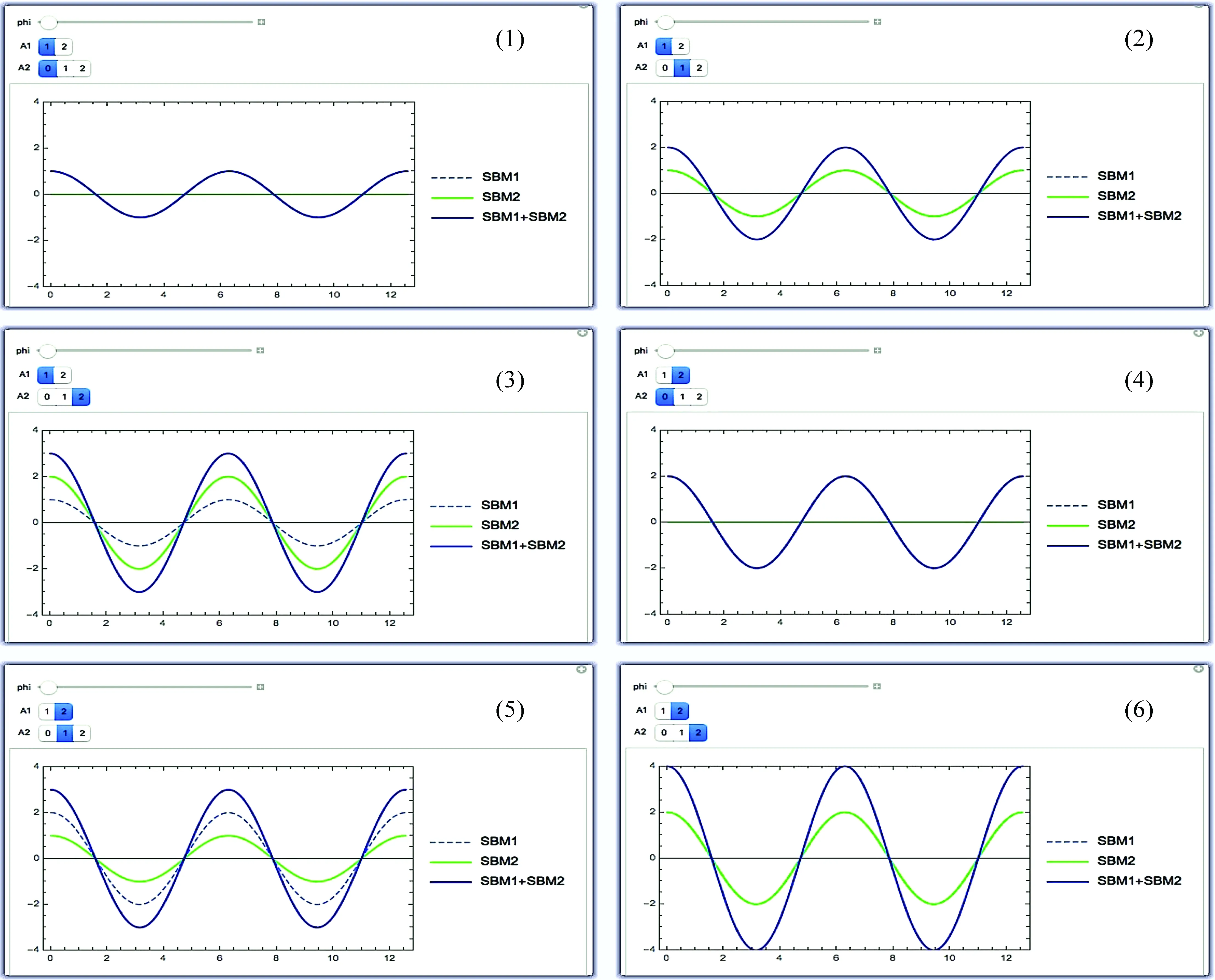
圖1 簡諧振動圖像(1) 振幅A1=1的分振動瞬時簡諧振動圖像; (2) 振幅A1=1、A2=1的分振動合成后的瞬時簡諧振動圖像； (3) 振幅A1=1、A2=2的分振動合成后的瞬時簡諧振動圖像； (4) 振幅A1=2的分振動瞬時簡諧振動圖像； (5) 振幅A1=2、A2=1的分振動合成后的瞬時簡諧振動圖像； (6) 振幅A1=2、A2=2的分振動合成后的瞬時簡諧振動圖像

圖2 某分振動改變相位時的合簡諧振動瞬時圖像對比

兩個方向垂直的簡諧振動可以合成各種奇特的曲線圖型, 由在互相垂直的方向上的兩個頻率成簡單整數比的簡諧振動所合成的規則的、穩定的閉合曲線被稱為李薩茹圖形。在此理論基礎上, 使用李薩茹圖形可以測量出兩個信號的頻率比與相位差, 常利用的工具是示波器, 并用以測定頻率或相位差。

如兩個簡諧振動方程分別為x=cosωt和y=cos(ωt+φ),通過對ω和φ的賦值,分別針對兩個分振動振幅相同時和振幅成比例時的合成情況, 使用Mathematica的命令進行質點運動的動態演示, 并配以合成運動的穩定軌跡圖, 命令語句如下：

w=2/3; phi=Pi/4;

{Button["1.0", w=1; phi=0 Pi;],

Button["1.1/6", w=1; phi=Pi/6;],

Button["1.1/4", w=1; phi=Pi/4;], Button["1.1/3", w=1; phi=Pi/3;],Button["1.2/3", w = 1; phi = 2 Pi/3;], Button["2.0", w=2; phi = 0 Pi;], Button["2.1/4", w=2; phi=Pi/4;], Button["2.1/2", w=2; phi=Pi/2;], Button["3.1/2", w=3; phi=Pi/2;], Button["1.5.1/4", w=1.5; phi=Pi/4;], Button["1.5.1/2", w=1.5; phi=Pi/2;], Button["2.5.1/4", w=2.5; phi=Pi/4;], Button["2.5.1/2", w=2.5; phi=Pi/2;]}

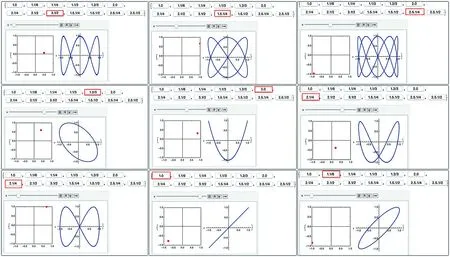
圖3 Mathematica動畫運行的部分圖形

Animate[{ParametricPlot[{Cos[t], Cos[w t+phi]}, {t, u, u+0.01}, Mesh -> {Range[u, u+0.01]}, MeshStyle -> {Red, PointSize[Large]}, Frame -> True, PlotRange -> 1], ParametricPlot[{Cos[t], Cos[w t+phi]}, {t, 0, 10 Pi}]}, {u, 0, 10 Pi}, AnimationRunning -> False]

1.2 惠更斯定理的圖形演示

圖4 縫半寬時單縫衍射下的惠更斯定理動畫瞬時圖像

惠更斯原理是一種用來分析、解釋波動如何行進的理論. 惠更斯認為, 波在傳遞過程中, 波前上任何一點都可視為一個新的點波源, 這些點波源將會往前進的方向產生新的波, 而波的下一時刻的波形便是由這些點波源波形疊加合成的結果。我們使用惠更斯原理解釋波的衍射現象, 發現平面波在到達一寬度與波長相近的縫時, 縫上各點都可以看做新的波源, 做出它們的包絡就可以得到新的波前, 此時波可以繞過障礙物向前傳播, 不過此時平面波的形狀發生改變, 邊緣處會發生波前彎曲. 并且縫的寬度相對波長越小, 衍射現象越明顯. 運用Mathematica命令制作動畫, 改變縫的寬度來演示惠更斯定理, 其中圖4展示了動畫運行過程的部分圖形, 可讓學生快速理解知識。運行如下命令：

{Button["0.5", {l=0.5, p=0.125}], Button["1", {l=1, p=0.25}], Button["2", {l=2, p=0.5}], Button["4", {l=4, p=1}]}

Animate[

Graphics[

Table[Circle[{n, 0}, t, {0, Pi}], {n, -l, l, p}], Axes -> True, PlotRange -> {{-7, 7}, {-0.2, 2 Pi}}, Frame -> True,

FrameTicks -> {{{-2 Pi, -Pi, 0, Pi, 2 Pi}, None}, {{-6, -4, -2, 0, 2, 4, 6}, None}}, Epilog -> {Rectangle[{-7, 0}, {-l, -0.2}], Rectangle[{7, 0}, {l, -0.2}]} ], {t, 0, 2 Pi}]

2 結語

利用先進的軟件Mathematica, 可以通過簡單的計算機語言, 直觀生動地展示出物理圖像, 讓學生可以在簡短的課堂教學中, 更快速地明確普通物理的相關知識, 激發學生的學習熱情。現代化教學需要教師解放教學思想, 開拓思路, 適當地利用多媒體軟件及計算軟件輔助教學, 通過教學模式的創新提高教學效率。本文中筆者只是應用Mathematica的強大的動畫繪圖功能, 還有許多豐富的功能等待利用。在當下的信息時代, 希望有更多的高校教師能更加有效地利用不同軟件, 恰當地將普通物理的知識學習與其結合, 共同 促進新型普通物理教學模式的發展。本文中的所有程序運算全部在Mathematica軟件官方云網站平臺(http://develop.open.wolframcloud.com/app/)進行。

[1] 鮑四元,孫洪泉,陳旭元.Mathematica在振動波問題中的應用[J].物理與工程,2010,20(4):49-51,64. Bao Siyuan, Sun Hongquan, Chen Xuyuan. Application of Mathmatica in the vibration wave problems[J]. Physics and Engineering, 2010, 20(4): 49-51, 64. (in Chinese)

[2] 柴連明,高偉.Mathematica與基礎物理教學[J].無線互聯科技,2014(7):257-258. Chai Lianming, Gao Wei. Mathematica and basic physics teaching[J]. Wireless Internet Technology, 2014(7): 257-258. (in Chinese)

[3] 洪洋.醫用物理學[M].北京:高等教育出版社,2014.

[4] Wolfman S. Mathematica全書(特別版)[M].周孝方譯.西安:西安交通大學出版社,2002.

[5] 韓克禎,耿雪.Mathematica軟件在波動教學中的應用[J].物理通報,2013(3):70-72. Han Kezhen, Geng Xue. The application on Mathematic in wave teaching[J]. Physics Bulletin, 2013(3):70-72. (in Chinese)

[6] 張新,倪致祥.基于Mathematica的振動傳播演示[J].阜陽師范學院學報：自然科學版,2008,25(2), 31-33. Zhang Xin,Ni Zhixiang. Vibration propagation’s demonstration based on Mathematica[J]. Journal of Fuyang Teachers College(Natural Science),2008,25(2), 31-33. (in Chinese)

APPLICATIONS OF MATHEMATICA IN GENERAL PHYSICS TEACHING

Liu Xin Zhao Li’ang Yu Wenjing Yang Huazhe

(Department of Physics and Biophysics, School of Fundamental Sciences, China Medical University, Shenyang Liaoning 110122)

Traditional teaching method of general physics in colleges and universities is abstract and complicated, which is limited and unfavorable for the comprehension of knowledge and interests in learning for most students. As a potential solution, the application of some computer software in teaching is considered to overcome the above-mentioned problems by enriching the classes. We analyzed some typical physical cases on vibration and waves via Mathematica by using the powerful animation and drawing function of the software. The calculated content would be more intuitive visualization, animation and intuition in the teaching through the combination of Mathematica and the traditional teaching method of basic physics knowledge. It would be helpful for students to get better and faster understanding of physical theories by introducing Mathematica into physics teaching. In addition, it can stimulate a lot of interests of studentsin physics knowledgeand cultivate theirability of independent thinking, which also promotes the efficiency of classroom teaching.

Mathematica; general physics; teaching method

2016-10-19

國家自然科學基金(編號：81500897)；國家留學基金(編號：201408210385)；遼寧省教育廳一般項目(編號：L2013285)。

劉鑫，女，助教，主要從事物理學的科研與教學研究,xliu13@cmu.edu.cn。

楊華哲，男，副教授，主要從事物理學的科研與教學研究,hzyang@mail.cmu.edu.cn。

劉鑫，趙里昂，于文晶，等. Mathematica在普通物理教學中的應用[J]. 物理與工程，2017，27(2)：51-55.