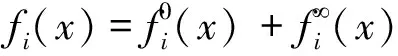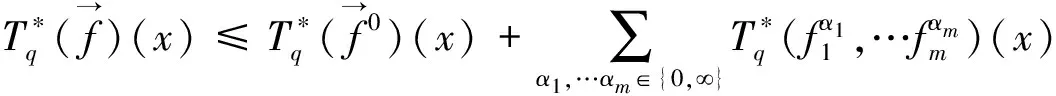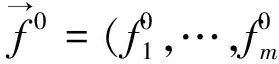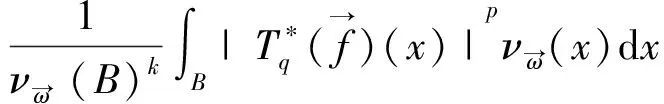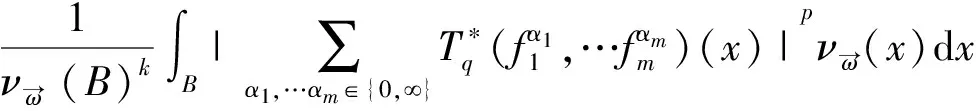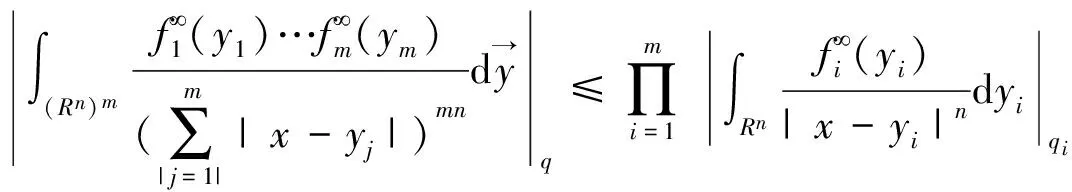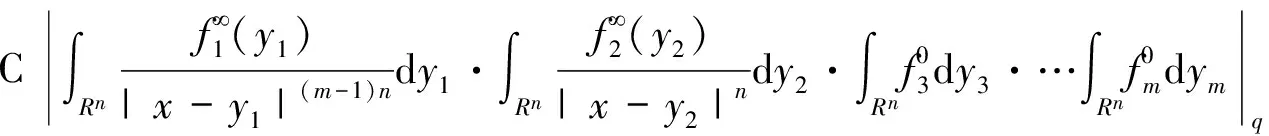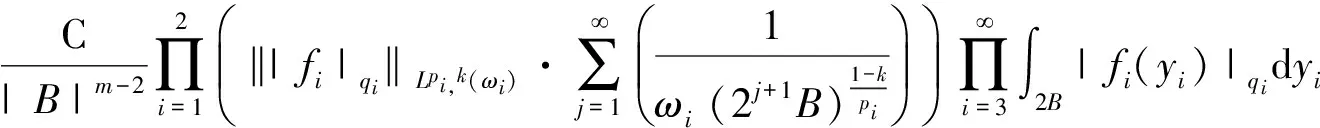向量值多線性極大奇異積分算子的有界性研究
張慧慧, 駱雯琦
(上饒師范學院 數學與計算機科學學院,江西 上饒 334001)
?
向量值多線性極大奇異積分算子的有界性研究
張慧慧, 駱雯琦
(上饒師范學院 數學與計算機科學學院,江西 上饒 334001)
利用一類多線性反H?lder不等式,得到了向量值多線性極大奇異積分算子在加權Morrey空間中的有界性。
向量值多線性極大奇異積分;加權Morrey空間;矢量權;多線性反H?lder不等式
1 引言及主要結論
眾所周知,多線性算子理論在調和分析的研究中起著重要的作用。2002年Grafakos和Torres[1]系統地研究了如下形式的多線性奇異積分算子:
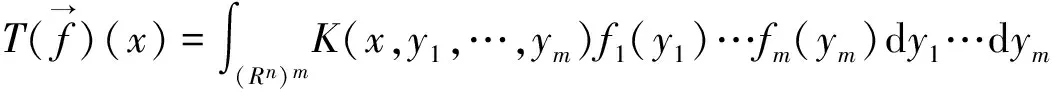

(1)
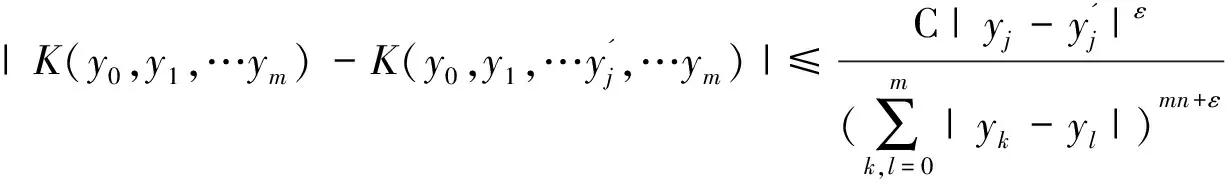
(2)


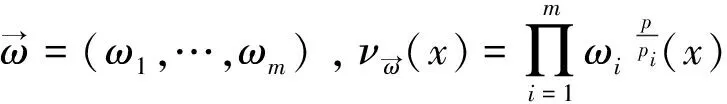
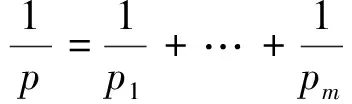
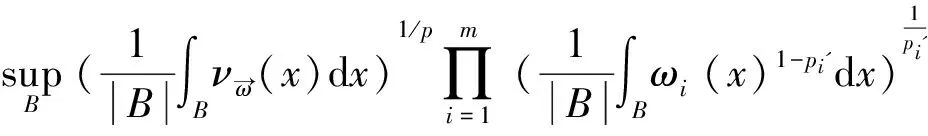
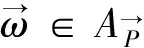
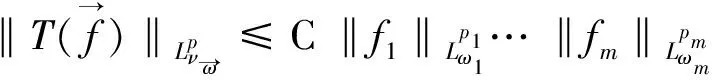
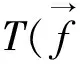
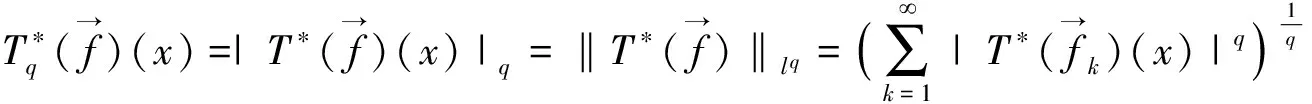



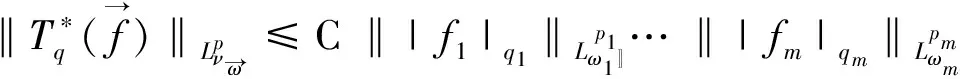
(3)
上世紀30年代,Morrey[4]通過引入著名的 Morrey空間Mp,λ(Rn)來研究二階橢圓微分方程局部解問題,這里Mp,λ(Rn)的定義為
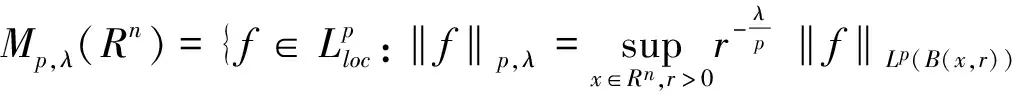
其中0≤λ 2009年,Komori以及Sharai[5]首次引入了加權Morrey空間Lp,k(ω),其定義為 在給出本文主要結論之前,先介紹AP權函數類的定義。 定義1.2[7]假設ω(x)是一個非負局部可積函數,若對所有的邊長與坐標軸平行的方體Q,均有 其中1 根據H?lder不等式,可得Ap?Aq(1 本文主要結論如下: 在給出定理1.1的證明之前,我們先給出一些證明過程中需要的引理。 對任一方體B,如果ω滿足ω(2B)≤Cω(B),其中C為和ω以及B無關的常數,則我們稱ω滿足二倍測度條件,記為ω∈Δ2。 引理2.1[8]如果ω∈Ap(1 引理2.2[8]如果ω∈Δ2,則存在大于1的常數C,使得ω(2B)≥Cω(B)。 引理2.3[9](多線性反H?older不等式)如果ωi∈Ar,其中r為大于1的任意實數,則對任意的方體 B?Rn,存在一個和方體B無關的常數C,使得 根據引理2.3,我們可得如果ωi∈Api,則有 (4) (5) |yi-x0|<2|x-yi|。然后類似于文獻[5]第226頁中的相關方法,我們有 (6) 故根據引理2.1和2.2,可得 (7) α1=α2=,α3=α4=…=αm=0這種情形,因為其余的情形計算過程都是類似的。首先根據(1),我們有 接下來給出∫2B|fi(yi)|qidyi的估計。……
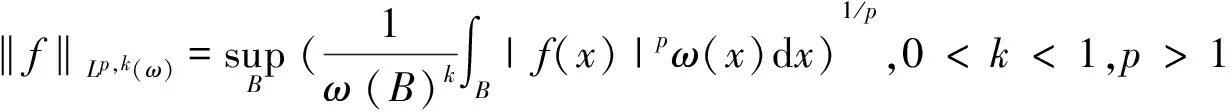
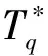
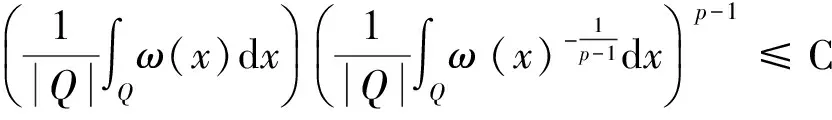
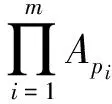
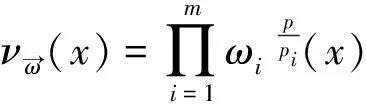
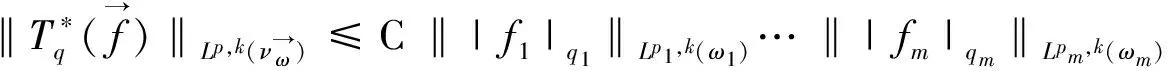
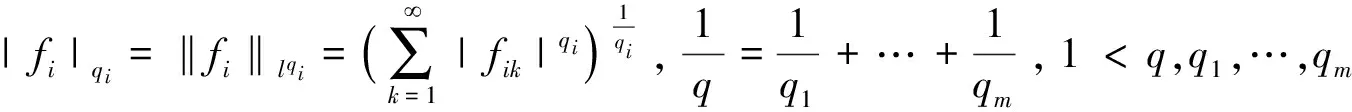
2 本文主要引理
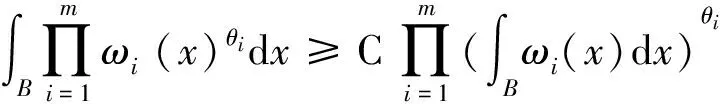
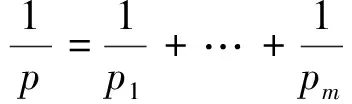
3 定理1.1的證明