基于GPS的無人機天線自動跟蹤系統

郭倩倩 周曉慧

(杭州電子科技大學信息與控制研究所 浙江 杭州 310018)

基于GPS的無人機天線自動跟蹤系統

郭倩倩 周曉慧

(杭州電子科技大學信息與控制研究所 浙江 杭州 310018)

針對解決無人機飛行探測中定向天線跟蹤問題，設計一種新型的基于GPS和單片機的天線自動跟蹤控制系統。通過詳細比較GPS跟蹤的三種算法，確定圓球模型算法對于一定跟蹤精度范圍，可完全替代平面模型和橢球模型，減少了計算量。根據圓球模型算法對系統軟硬件進行開發與設計，系統通過無人機通信數據鏈獲取無人機的位置信息，結合系統自身的GPS位置信息、羅盤的方位信息，運用圓球模型算法計算出天線需轉動的方位角和俯仰角，通過單片機控制天線對準無人機。實驗測試結果表明，對于10公里范圍內的跟蹤，系統的跟蹤精度滿足設計的要求，具有較強的實用價值和推廣意義。

無人機 GPS 天線 跟蹤

0 引 言

近年來無人機作為一種新型的探測工具得到了國家和社會各界的較大關注。在無人機飛行過程中，無人機與地面站之間通過無人機通信數據鏈傳輸數據，通信數據鏈分為上行鏈路和下行鏈路。上行鏈路是地面站將對無人機的控制信息使用Mavlink(Micro Air Vehicle Link)協議打包后，通過天線發送至無人機控制器，無人機控制器根據協議解包后響應控制信息。下行鏈路是無人機控制器將飛行數據打包，和采集的圖像編碼后，一并通過天線實時回傳給地面站數據接收系統。因此，天線信號的強弱直接影響到無人機飛行的穩定性和采集圖像的質量。目前，天線自動跟蹤方法有步進跟蹤、圓錐掃描跟蹤、單脈沖單通道跟蹤和程序跟蹤等[1-4]。其中步進跟蹤方法設備簡單，價格低廉，但其天線波束不能停留在被跟蹤目標的方向上，而是在目標方向周圍不停地擺動；圓錐掃描跟蹤方法是驅動天線在空間中做圓錐式掃描以獲取最大信號電平，從而得到目標角誤差信號，但由于饋源永遠是偏離天線拋物面的焦點，因而天線的增益大大降低[5]；單脈沖單通道跟蹤方法的跟蹤速度和精度比步進跟蹤和圓錐掃描方法高，但設備復雜。對于無人機來說，程序跟蹤是一種簡單高效的跟蹤方法，文獻[6]運用橢球模型算法計算無人機的位置信息，文獻[7]提出用圓球模型計算相對地理位置。橢球模型是目前應用比較廣泛的一種模型，但計算量比圓球模型大。本文比較了以上兩種算法和同樣應用廣泛的平面模型，確定圓球模型在無人機跟蹤的一定精度范圍內，完全可以替代橢球模型和平面模型，并設計及開發了天線跟蹤系統的軟硬件。經實驗測試，對于10公里范圍內的跟蹤，系統跟蹤性能良好，維護方便。

1 系統整體設計

天線自動跟蹤系統由控制器部分、數據收發部分組成，如圖1所示。

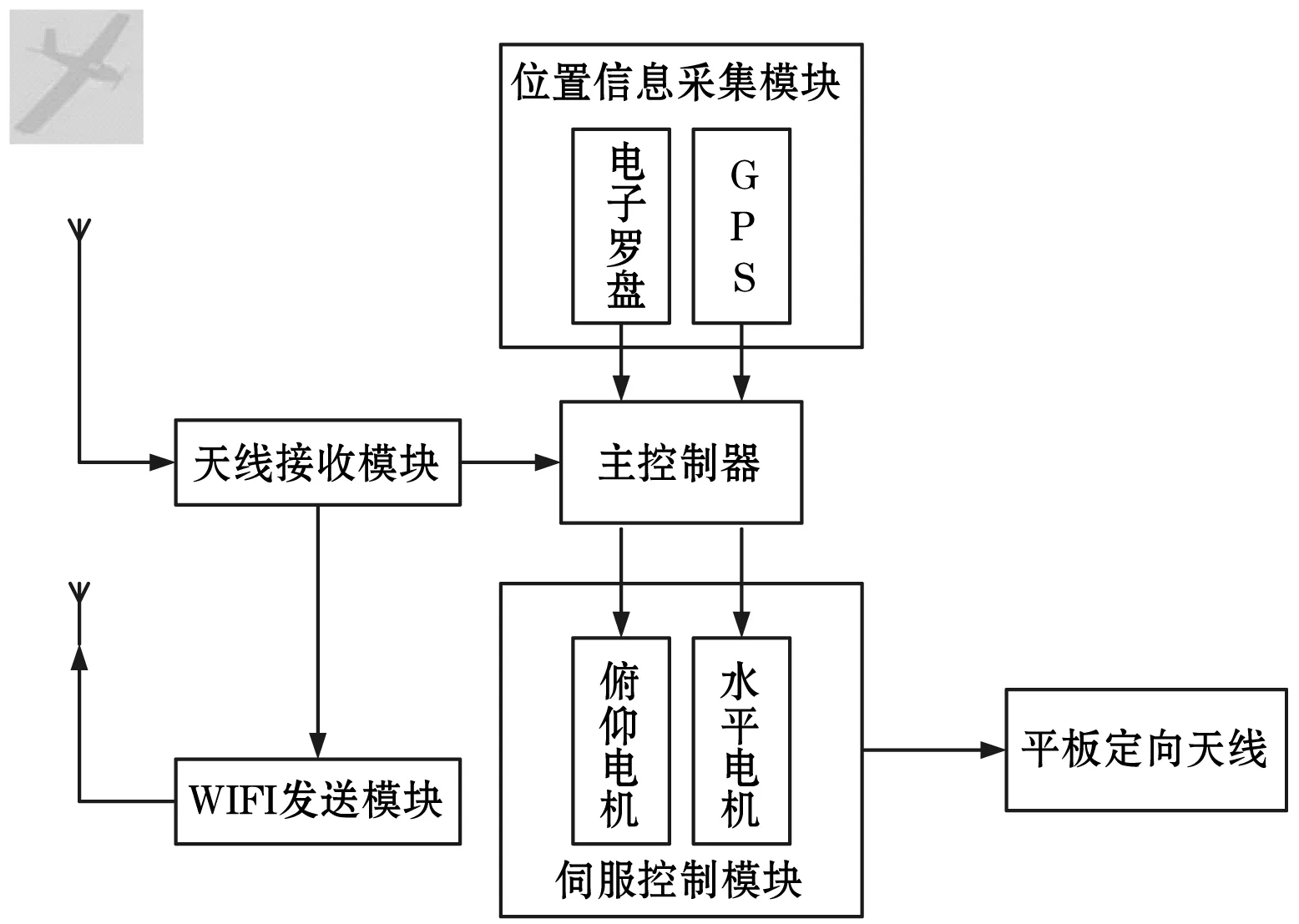
圖1 天線跟蹤系統組成示意圖

系統通過天線模塊，將平板定向天線接收到的無人機飛行數據送入主控制器進行分析處理，提取無人機當前位置的經度、緯度、海拔信息。同時采集本系統的GPS數據、電子羅盤數據，得到系統所處地理位置的經緯度和海拔信息。根據無人機和系統的兩組GPS數據計算出平板定向天線需轉動的角度，控制系統的水平伺服電機和俯仰伺服電機，使天線對準無人機。在控制天線轉動的同時，系統將接收到的數據通過WiFi發送到周圍的地面控制站，保證無人機與地面控制站的正常通信。

2 跟蹤系統算法

平面模型、圓球模型和橢球模型是三種常用的跟蹤算法，通過獲取系統和目標點的位置信息，運用跟蹤算法計算出天線的方位角和俯仰角。本系統距目標點的最遠距離限制為10 km，海拔高度差為200 m，系統選用的天線波瓣寬度為10°，因此方位角和俯仰角的計算誤差需小于一個數量級，即1°。

設A點為觀測點，其大地坐標為(B0,L0,H0)，G為目標點，其大地坐標為(B1,L1,H1)，其中B0、B1，L0、L1，H0、H1分別表示A、G兩點的緯度、經度和海拔高度。G在地面上的投影點為B，設N為真北方向，地球半徑為R，方位角的計算，以真北為0°起點，由東向南向西順時針旋轉360°。

2.1 平面模型

平面模型是將球面上已知經度、緯度的兩個點分別看做平面直角坐標系中的兩個坐標點，對兩點的經度、緯度分別做差，差值作為兩邊的長度，再利用反正切函數計算得方位角。方位角計算公式為：

(1)

根據球面上兩點之間距離公式：

d=Racos(sin(B0)sin(B1)+cos(B0)cos(B1)cos(L1-L0))

(2)

將球面距離作為直線距離計算目標點G相對于觀測點A的俯仰角：

(3)

2.2 圓球模型

圓球模型如圖2所示。

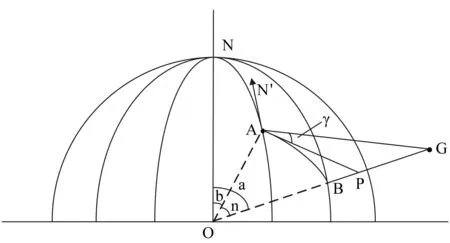
圖2 圓球模型

把地球近似為一個圓形球體，設二面角B-ON-A為∠ON，弧AB是A、B兩點的球面距離，AN′方向為A點所在處的正北方向，面PAN′是A點的參考水平面[7]，則∠PAG為天線的仰角，設為γ，∠N′AP(即球面三角形ABN中的∠A)為方位角，設為θ，則根據三面角余弦公式：

cos(n)=cos(a)cos(b)+sin(a)sin(b)cos(∠ON)

(4)

將已知數據帶入得：

cos(n)=cos(90°-B1)cos(90°-B0)+sin(90°-B1)sin(90°-B0)cos(L1-L0)

(5)

根據球面正弦公式：

(6)

得方位角：

(7)

做面AGO沿AGO的橫切面，根據橫切面的三角形正弦定理，得俯仰角：

(8)

2.3 橢球模型[11-13]

采用的坐標系為左手站心地平直角坐標系，橢球模型如圖3所示。左手站心地平直角坐標系是以測站法線(切平面)和子午線方向為依據的坐標系，以觀測點天線位置A為原點，以站心A點的法線為Z軸(指向天頂為正)，在切平面上以子午線方向為X軸(向北為正)，Y軸與X、Z軸正交(向東為正)，構成左手站心地平坐標系，記為A-NEU。圖中以橢球中心O為原點，起始子午面與赤道面的交線為X軸，橢球的短軸為Z軸(向北為正)，在赤道面上與X軸正交的方向為Y軸(向東為正)，構成右手直角坐標系O-XYZ。設A、G兩點的空間直角坐標分別為(X0，Y0，Z0)、(X1，Y1，Z1)，對同一空間，直角坐標系與大地坐標系參數間的轉換關系如下：

(9)

式中，L、B、H為地心大地坐標；N為參考橢球的卯酉圈曲率半徑；e為第一偏心率。

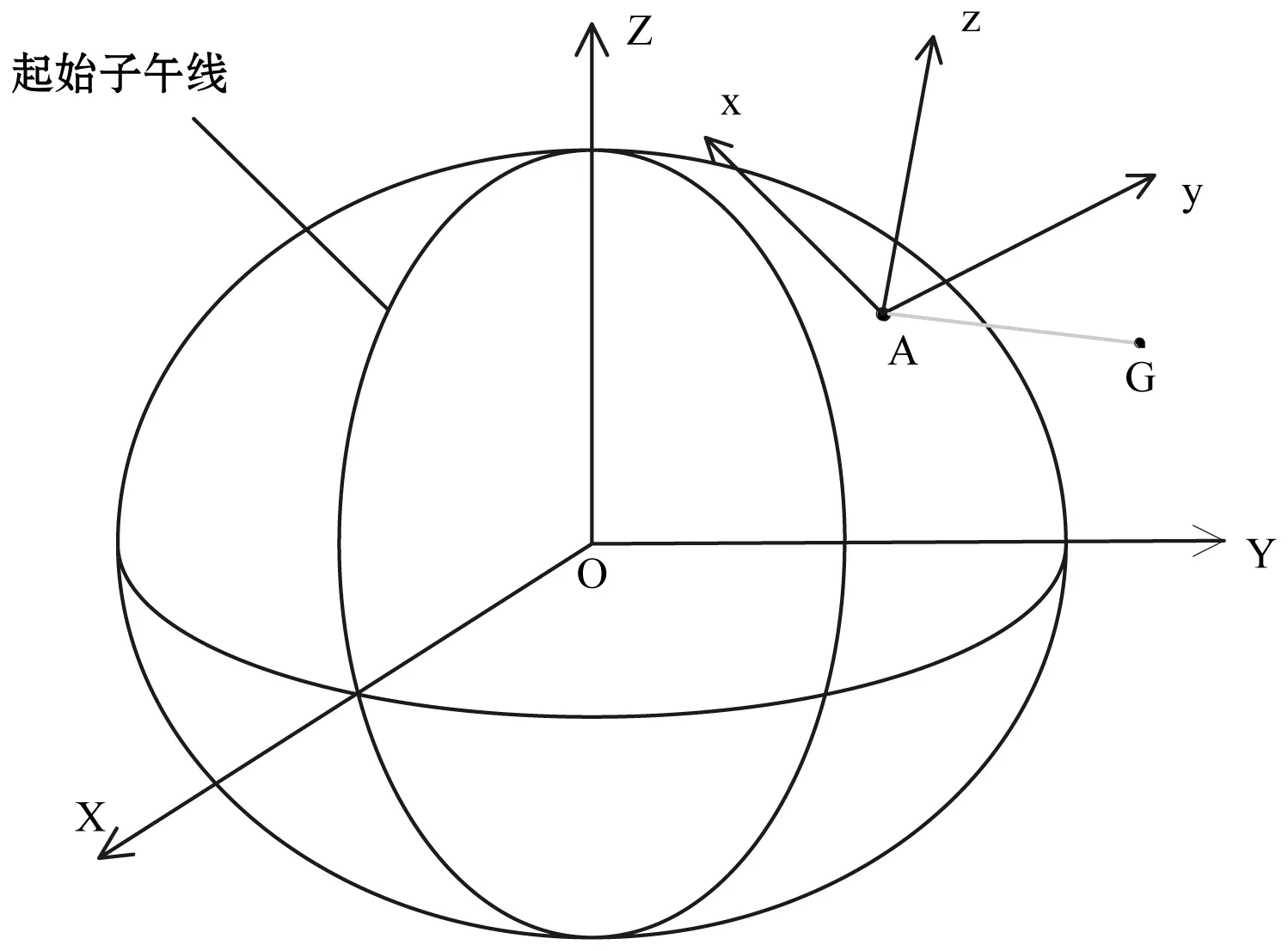
圖3 站心地平直角坐標系與空間直角坐標系

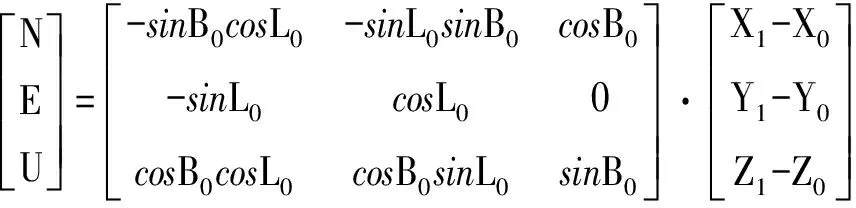
(10)

則方位角為：

θ=tg-1(E/N)

(11)

俯仰角為：

(12)

2.4 三種模型的比較

對以上三種模型，首先在理論上作比較，以北半球作為參考，圖2中的A、G點分別在低、中、高低緯度選取不同的四組數據，并且保證觀測點和目標點之間的距離在10 km以內，海拔差值在200 m以內，計算方位角和俯仰角，結果見表1所示。

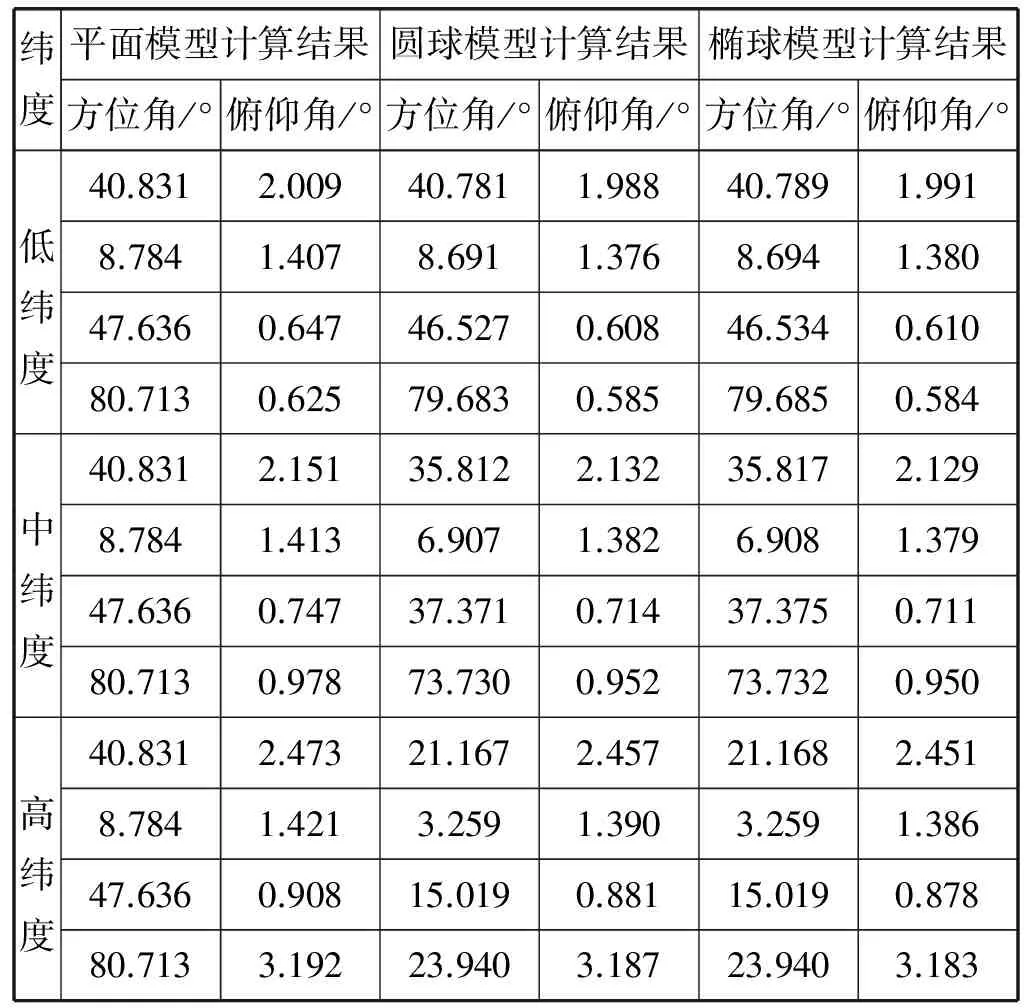
表1 三種模型計算的方位角及俯仰角比較

由表1的計算結果得出，在低緯度地區，利用平面模型計算的方位角與橢球模型計算的方位角的誤差已經超過1°，利用圓球模型計算的結果接近于橢球模型，在低中高緯度地區，誤差均小于1°。由于橢球模型涉及到矩陣運算，計算量大，對處理器的性能要求較高，并考慮系統可測范圍相對地球表面空間來說距離短，高度低，因此初步選擇圓球模型作為本系統的跟蹤算法來計算平板定向天線需轉動的方位角和俯仰角，此方案實際飛行中是否可行，需進一步飛行試驗驗證。

3 系統軟硬件設計

系統控制器主要由主控制器、位置信息采集模塊、伺服控制模塊組成，可以進行高精度的位置信息采集與處理，并控制水平和俯仰伺服電機的轉動，俯仰伺服電機的可控制角度為0～100°，水平伺服電機則可進行360°連續旋轉控制，實現了對無人機的全方位跟蹤控制。

3.1 主控制器

考慮所選算法的運算量，主控制器采用意法半導體公司的32位單片機STM32F107，其搭載的Cotex-M3內核，采用擁有獨立指令總線和數據總線的帶有分支預測的3級流水線哈佛結構。工作頻率最高能達到72 MHz，在存儲器的0等待周期訪問時可達1.25 DMIPS/MHz，而且具有定時器、通用串行收發器UART、集成總線IIC、以太網模塊等多種外設支持[8]，完全滿足系統需求，而且其成本低，可靠性高，應用廣泛。

3.2 位置信息采集模塊

位置信息采集模塊主要由電子羅盤和GPS兩部分組成，電子羅盤用于方位角的采集，GPS部分用于位置信息采集。

考慮算法對航向精度的要求和室外溫差變化大，-20～40 ℃都會使用，所以電子羅盤選擇帶溫度補償的霍尼韋爾公司的HMC5983芯片，該芯片內置驅動電路，體積小，帶溫度補償，低干擾AMR傳感器與12位ADC可達到2毫高斯分辨率，測量精度可達到1°。其與主控制器通過IIC(Inter-Integrated Circuit(內部集成電路總線))通信，使用簡單。

GPS選用最新的u-blox公司的NEO-M8Q天線模組，NEO-M8Q能夠同時獲取跟蹤不同的GNSS(全球導航衛星系統)：并行接收GPS(QZSS)和GLONASS或北斗，或同時接收GLONASS和北斗。此模組專門適用于即使在GPS信號差的環境下(如城市峽谷)都需要最高的可用性和準確性的性能應用。NEO-M8Q模組的功耗較低，冷啟動速度快，定位精度可達到0.5～1 m，滿足要求不是很高的測繪級使用要求。根據官方解決方案，設計電路如圖4所示。

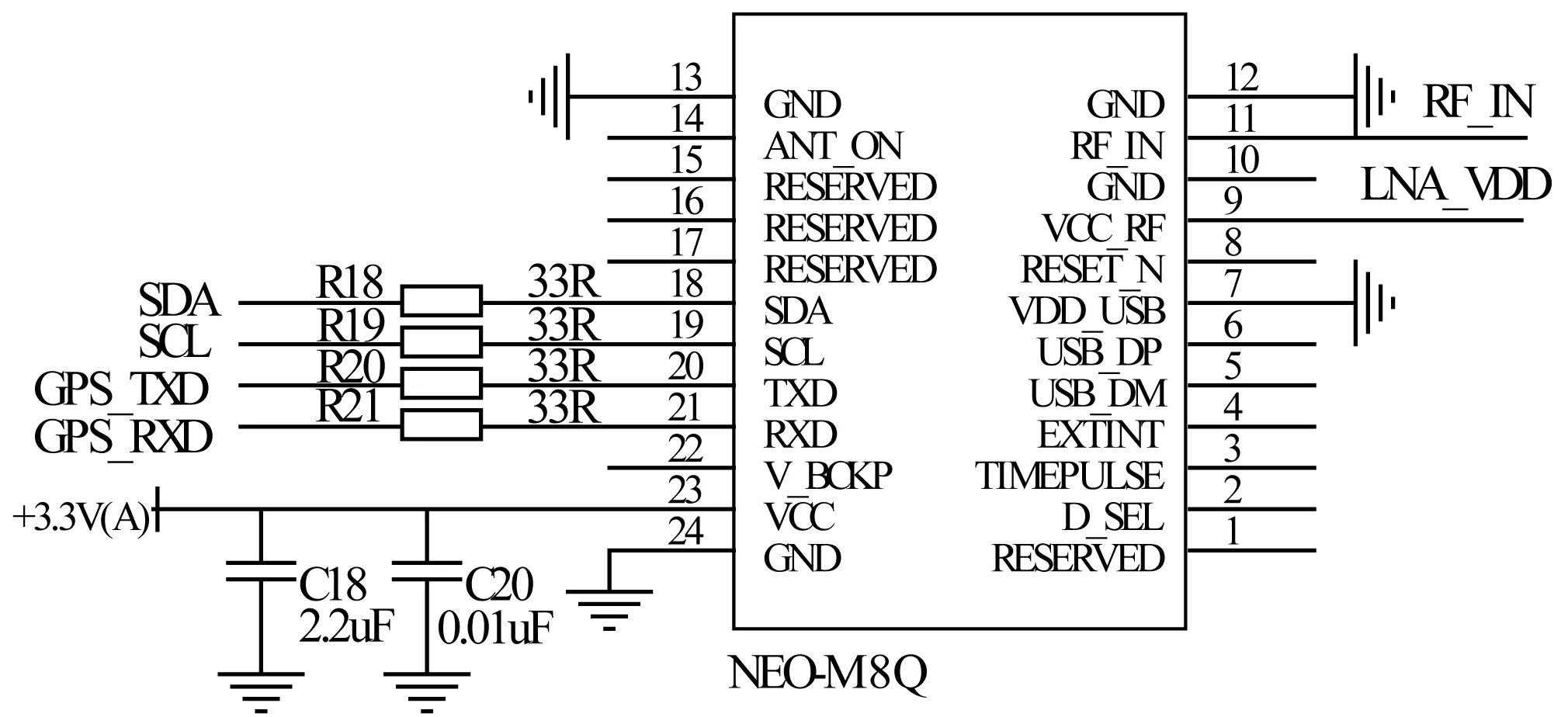
圖4 GPS模塊電路圖

在測試中發現，周圍環境對GPS天線的干擾比較大，而且在建筑物較多的地方，GPS信號較弱，因此，在GPS天線部分增加一個濾波放大電路，使用官方推薦的SKY65709GPS天線專用信號濾波放大芯片，原理如圖5所示。

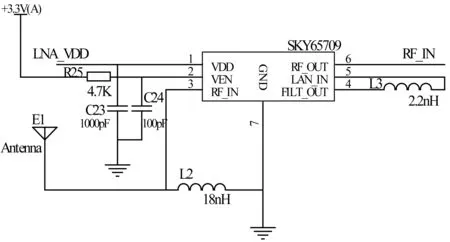
圖5 GPS信號濾波放大電路

3.3 伺服控制模塊

系統伺服控制模塊可看成一個二自由度的云臺，控制平板定向天線的水平旋轉和俯仰轉動。云臺的轉動部分可以選擇直流電機、步進電機、舵機。直流電機需要配合編碼器實現定位，結構復雜，而且直流電機需要設計驅動電路，增加系統成本。步進電機直接輸入PWM脈沖個數，無需驅動電路，就可以實現一定角度的轉動，但是步進電機的定位是相對于前一位置，負載較大時使用會出現丟步，長時間使用會累積誤差，精度較低。而舵機控制直接使用PWM的脈沖寬度就可以控制舵機轉動角度，屬于絕對定位，沒有累積誤差，同步進電機一樣，無需驅動電路。因此，選擇舵機控制云臺轉動。

考慮控制精度、負載扭矩以及室外使用的環境，本系統選用春天SE-C4413V舵機，其重量僅為70 g，防水設計，可全天候使用，供電電壓7.4 V，最大輸出扭矩為25.6 kg·cm，最大轉速為400 °/s。舵機的轉角控制主要采用PID控制器來實現，PID控制具有算法簡單、魯棒性好、可靠性高等優點,被廣泛用于工業過程控制中。本舵機伺服控制系統采用電流環、速度環、位置環的三閉環控制方案[9-10]，如圖6所示。其中電流環采用PI控制，可以提高系統的快速性，及時抑制電流環內部的干擾；速度環采用P調節，可以減小舵機調節過程中的振蕩和超調；位置環的設計是整個控制系統的關鍵，它密切關系到系統的跟蹤性能與靜態精度，采用PID參數自整定控制。

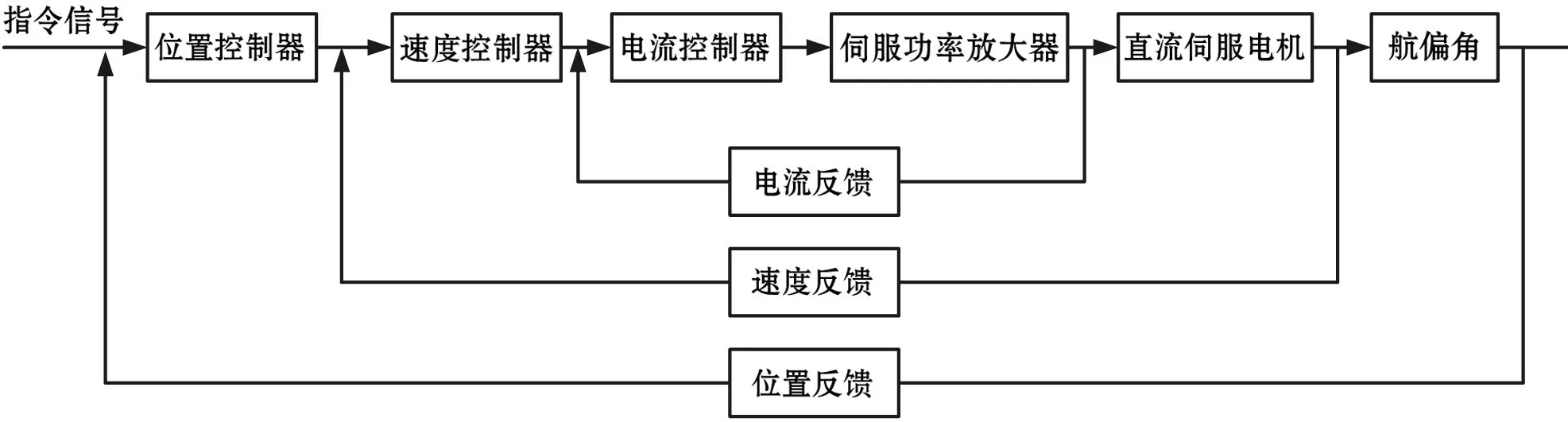
圖6 舵機工作原理框圖

3.4 軟件設計

軟件設計部分以C語言為開發語言，系統工作流程設計模式如下：

1) 自檢模式：系統開機后，進入自檢模式，旋轉校準電子羅盤，校準結束后，系統旋轉幾個固定位置，如正東仰角30度，正北仰角60度等，驗證系統各部件性能是否正常，是否可以正常工作。

2) 自動模式：系統自檢后，處于待機狀態，按下啟動工作按鍵，系統進入自動模式。

3) 搜索模式：當系統沒有及時跟蹤到無人機，無人機超出天線收發角度范圍，系統無法獲取無人機位置，此時系統自動切換為搜索模式，水平方向均勻設置12個位置，每個位置垂直方向舵機從0度到90度再回到0度，直到搜索到無人機信號為止。

4) 手動模式：當系統遇到角度計算錯誤、舵機出現故障等突發情況時，可以按下手動模式按鍵進入手動模式，此時舵機沒有輸入信號，系統可以手動調整角度，而其他模塊均正常工作。

根據系統功能需求，工作流程如圖7所示。

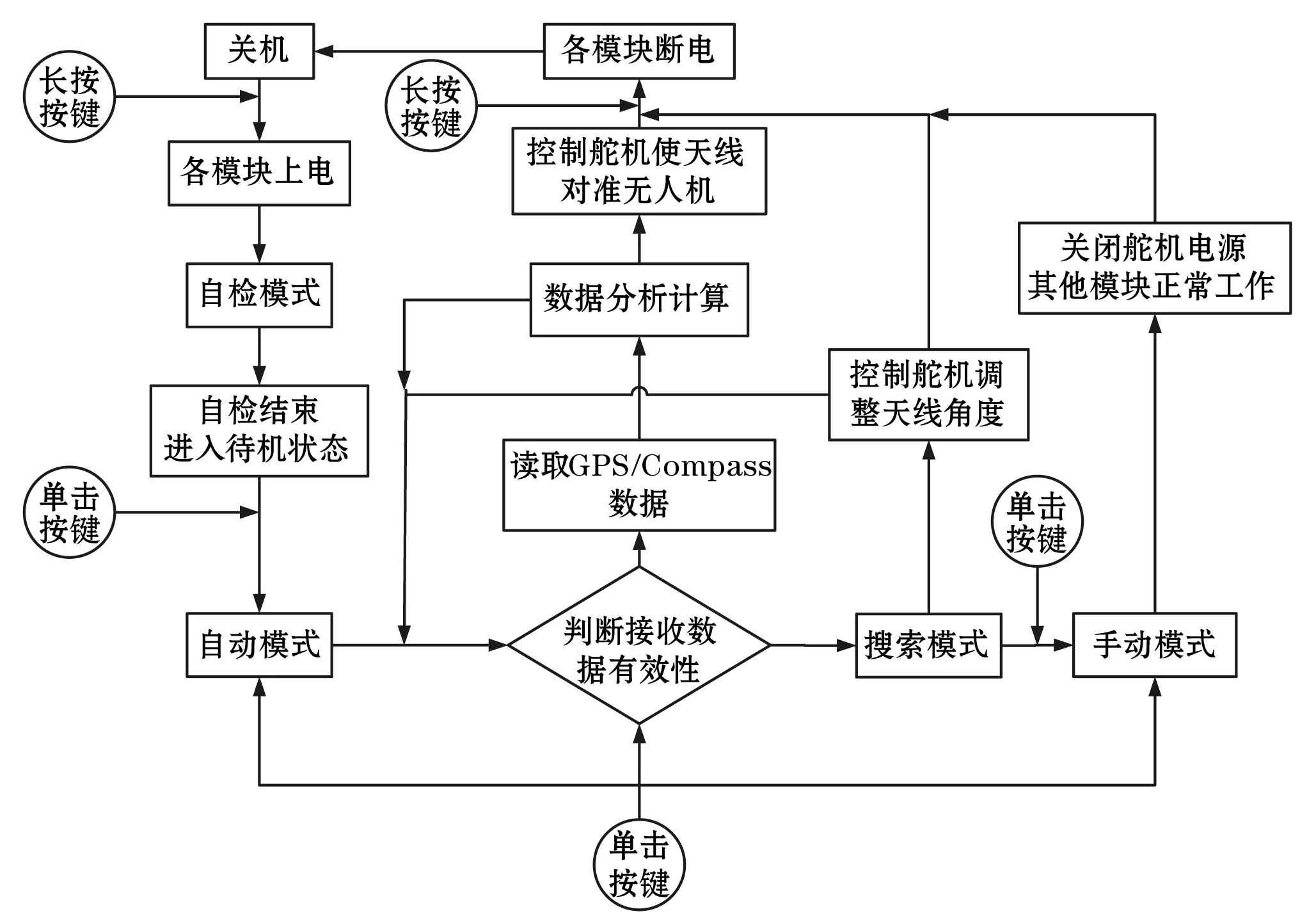
圖7 工作流程圖

4 實驗測試

對系統進行無人機飛行跟蹤的反復試驗測試，選取其中的一段飛行數據，經數據分析得天線跟蹤的俯仰角和方位角，并結合無人機實際的飛行數據，對比結果如圖8、圖9所示。

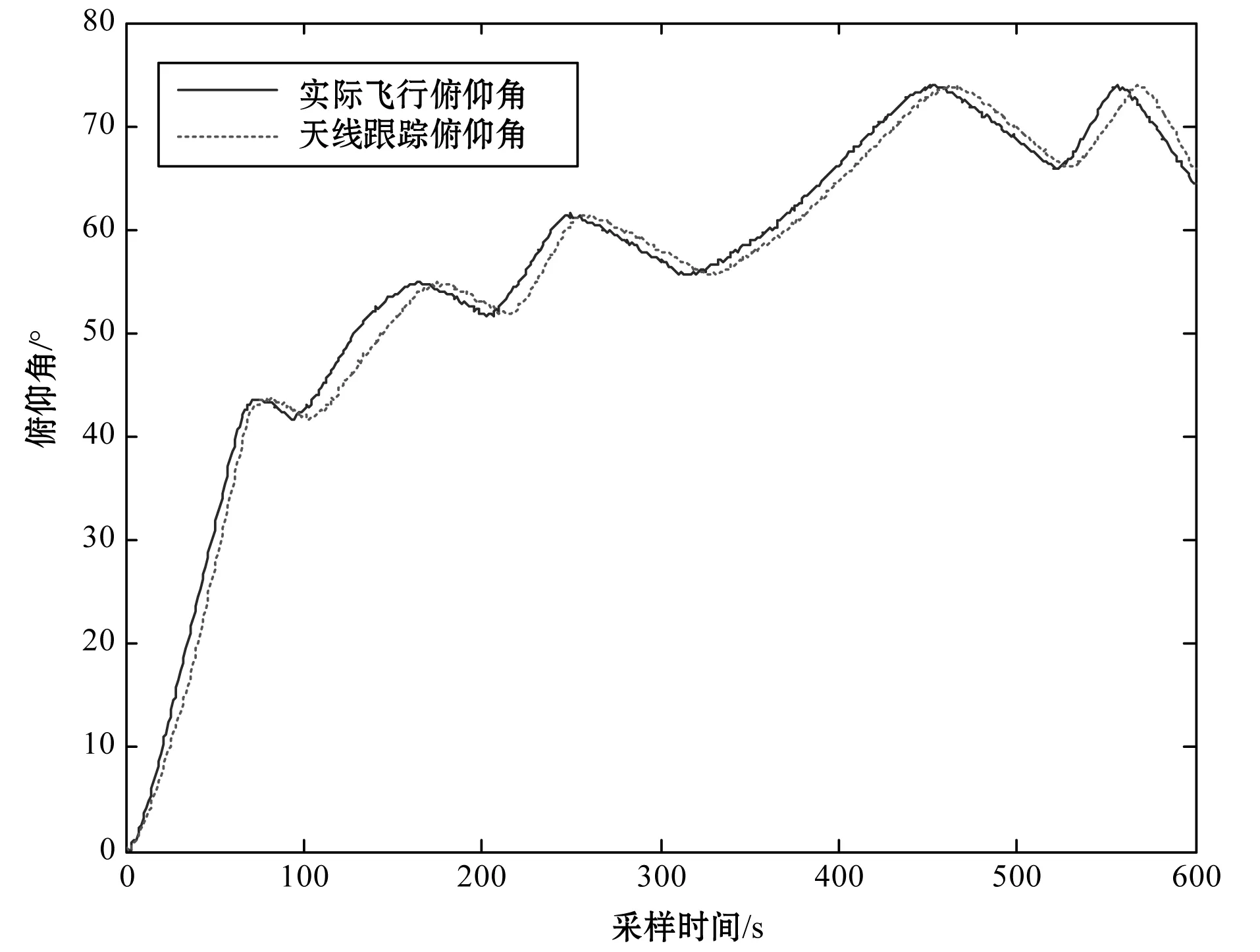
圖8 俯仰角跟蹤比較

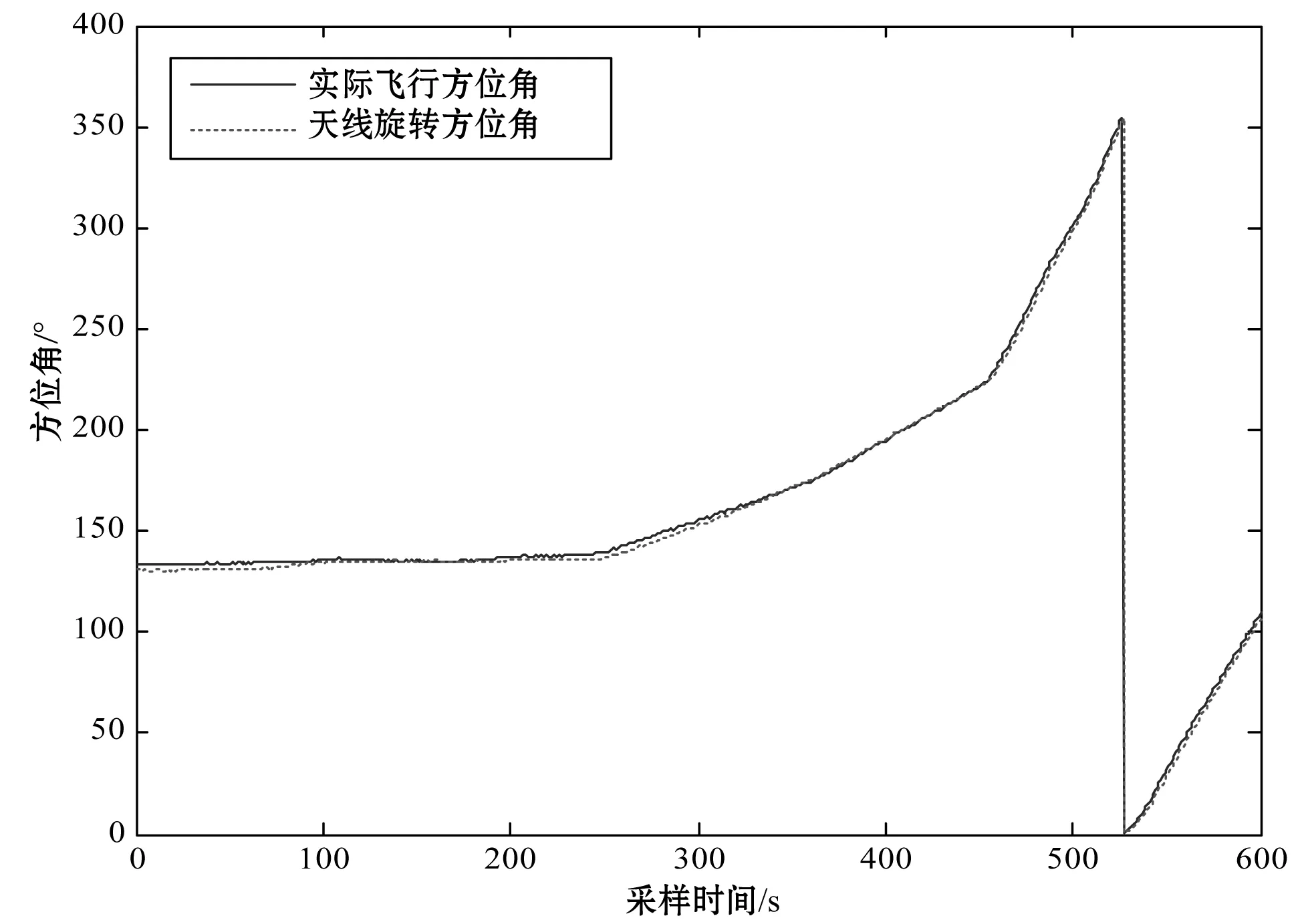
圖9 方位角跟蹤比較

經飛行測試證明，系統的天線跟蹤情況良好，雖然有延時存在，但誤差不超過5°，能保證信號和圖像的傳輸質量，此實驗也進一步證明了本系統選擇圓球模型來計算采集位置信息的方案是可行的。

5 結 語

本系統的設計，針對無人機飛行過程中的實際要求，選用低成本單片機、傳感器、舵機，結合GPS定位技術，實現天線自動跟蹤。系統硬件設計簡單，跟蹤程序高效可靠，通過模擬飛行實驗證明，圓球跟蹤算法對于本天線跟蹤裝置是滿足要求的，可以滿足數公里范圍內的無人機天線跟蹤需求，是具有實際應用價值的天線跟蹤裝置。

[1] 李正周,趙峰,楊士德,等.基于梯度法的對空中目標搜索與跟蹤[J]. 系統仿真學報, 2007, 19(5): 1078-1081.

[2] Han K, Guo W, Gao X. A step tracking on the SOTM[C]//IEEE International Conference on Computer Science and Information Technology. IEEE, 2010:214-216.

[3] 鐘水和, 王建, 潘堯成,等. 單通道單脈沖跟蹤系統自動校相的設計與實現[J]. 四川兵工學報, 2015, 36(7):97-99.

[4] 查長流, 丁希侖, 俞玉樹,等. 無人機定向天線自跟蹤系統研究[J]. 北京航空航天大學學報, 2016, 42(4):737-744.

[5] 孫興邦. 衛星天線自動跟蹤算法的研究[D].大連：大連海事大學, 2008.

[6] 黃偉, 周乃恩, 王誠,等. 一種無人機通信天線伺服系統的構建[J]. 電子技術應用, 2009, 35(6):98-101.

[7] 杜利明, 柴海莉.基于GPS信息的天線自跟蹤設計[J].微計算機信息, 2008, 24(9-1)：243-244.

[8] 沈建良, 賈玉坤, 周芬芬, 等.STM32F10X系列ARM微控制器入門與提高[M]. 北京：北京航空航天大學出版社, 2013: 1-7.

[9] 肖業偉, 吳稱列, 王正強, 等. 基于電動舵機優化控制的仿真研究[J].計算機仿真, 2015, 32(11): 321-324.

[10] 岳明凱, 李志霞, 王欣. 模糊PID算法的火箭彈舵機控制方法研究[J].沈陽理工大學學報, 2012, 31(3)：68-72.

[11] 季凱敏, 王解先. 利用大地坐標計算真方位角的兩種方法[J]. 工程勘察, 2009(4): 84-86.

[12] 徐紹銓, 張華海, 楊志強, 等. GPS測量原理及應用[M]. .武漢：武漢大學出版社, 2003: 11-14.

[13] 李宗春, 李廣云, 薛志宏, 等. 地球站天線方位/俯仰角嚴密計算方法的研究[J]. 無線電通信技術, 2003, 29(6): 30-32.

UAV ANTENNA AUTOMATIC TRACKING SYSTEM BASED ON GPS

Guo Qianqian Zhou Xiaohui

(InstituteofInformationandControl,HangzhouDianziUniversity,Hangzhou310018,Zhejiang,China)

A new automatic tracking and control system based on GPS and single chip is designed to solve the problem of directional antenna tracking in unmanned aerial vehicle (UAV) flight detection. By comparing the three algorithms of GPS tracking in detail, it is confirmed that the sphere model algorithm can completely replace plane model and ellipsoid model for certain range of tracking accuracy, and reduce the calculation amount. The software and hardware of the system are developed and designed according to the sphere model algorithm. The system obtains the position information of unmanned aerial vehicles (UAVs) through unmanned aerial vehicle (UAV) communication data link. Combining GPS position information and azimuth information of compass, the azimuth angle and pitch angle of the UAV are calculated by ball model algorithm. Through the single-chip control antenna aligned unmanned aerial vehicles. The experimental results show that the tracking accuracy of the system meets the design requirements for the tracking within 10 km, which has strong practical value and popularization significance.

UAV GPS Antenna Tracking

2016-04-25。浙江省公益項目(2015C34008)。郭倩倩，碩士生，主研領域：控制科學與工程。周曉慧，教授。

TP391

A

10.3969/j.issn.1000-386x.2017.06.017