問課哪能“效”如許 胸有丘壑“慢”中來
戎昕煒


【摘 要】“教育是慢的藝術”。教育一定要遵循孩子的自然成長規律和認知規律。本文結合初中數學課堂教學實踐工作,從教學入口“寬”些,知識體系“緊”些,問題設計“放”些,例題處理“變”些,教學評價“延”些這五個方面開展“慢”鏡頭教學。
【關鍵詞】數學課堂;“慢”鏡頭教學
“教育是慢的藝術”。教育一定要遵循孩子的認知規律和自然成長規律。真正有效的課堂,不在于用多快的速度把一個完整的知識體系呈現給學生,而在于是否教給了學生思維方法、基本原理和核心概念,在于是否根據學生的實際需要,在他們思維的節點上進行了放大。而數學知識有其特有的邏輯聯系,要讓學生理解掌握其中的聯系就需要一個過程,故在初中數學課堂教學中更有實施“慢”鏡頭教學的必要!我們開展“慢”鏡頭教學時可以朝以下“五個方向”努力探索。
一、教學入口“寬”些,搭建探究平臺
在全面實施素質教育的今天,“學困生”在教育工作中占有極其重要的位置,因此,我們在數學教學中要特別注重起點低、入口寬、過程慢。現結合案例“探索勾股定理”加以說明。
片段:(從數和形兩方面入手)
分組讓學生盡量準確地作出兩個直角三角形,兩直角邊分別為3cm和4cm,6cm和8cm,并測量手中的直角三角形(課前每人發了兩個全等的直角三角形)并根據測量結果完成下表:
師:觀察表中三組數據你能得到直角三角形三邊長度之間的關系嗎?
教師規范學生的語言表述并板書:a2+b2=c2。
師追問:a2的幾何意義是什么?
生: 以a為邊長的正方形的面積。
播放視頻,觀察勾股定理教學儀器中水面積的變化規律并總結。
分析與討論:本案例先從數和形兩方面切入,學生通過畫圖、測量和計算中感悟定理的猜想過程,并體現了從一般到特殊,再到一般的探索過程,并充分感受了聯想、類比的功效。
二、知識體系“緊”些,創建嚴密結構
數學復習課不是新授課,需不需要創設教學情境呢?其實,復習課更需要創設合理的教學情境以保證課堂教學的有效性,在情境中串起一堂課的主線,緩緩鋪開,讓學生自然進入深一步的學習。所以在選擇創設什么樣的合理情境時,應該以此情境能否很好地承載數學知識作為標準,否則將是舍本逐末。
如案例:八年級《特殊平行四邊形復習》
首先,老師拿出一張一般的三角形的紙片
師:你能否剪兩刀,剪出一個平行四邊形?并說出理由?
①當△ABC是什么三角形時,剪下來的四邊形ADEF為矩形?并說明理由?
②當△ABC是什么三角形時,四邊形ADEF為菱形?
③當△ABC是什么三角形時,四邊形ADEF為正方形?
在第③問的基礎上老師追問:四邊形DBCF是怎樣的特殊圖形?
老師通過此情境創設讓學生經歷知識網絡的形成.并采用圖解式板書讓學生更直觀地接觸知識點,迅速回憶起平行四邊形、矩形、菱形、正方形、梯形等四邊形的判定和性質及其內在聯系。并要求同學們必須做到能把各個章節中的知識聯系起來,能綜合運用,做到觸類旁通,領悟方法,從而幫助他們形成與發展創新意識、創新精神和創新能力。
三、例題處理“變”些,拓展思維效度
隨著新理念的不斷深入,探究活動貫穿整個初中數學課程,而通過“變式教學”對數學問題多角度、多方位、多層次的討論和思考,有意識、有目的地引導學生從“變”的現象中發現“不變”的本質,從“不變”的本質中探究“變”的規律,使相關知識融會貫通,使學生思維游刃有余。現結合浙教版九上《4.4相似三角形的性質及其應用(2)》中的一道題目為例來進行說明。
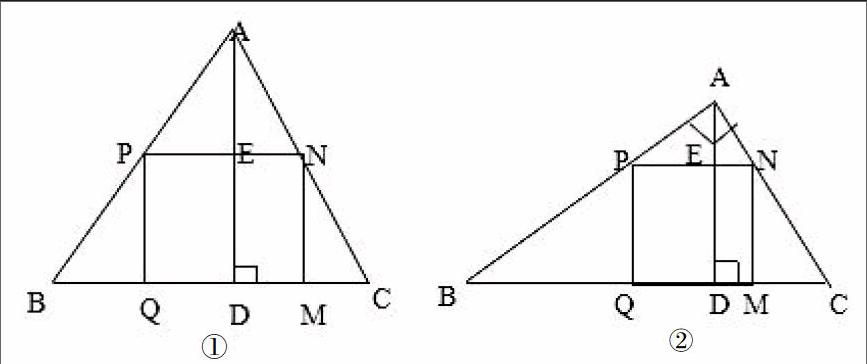
例題:如圖,△ABC是一塊銳角三角形余料,邊BC=120毫米,高線AD=80毫米,要把它加工成正方形零件,使正方形的一邊在BC上,其余兩個頂點分別在AB,AC上。這個正方形零件的長是多少?
個人認為,變式的方法可以有:
1.從靜態到動態
在原命題中,若點P為邊AB上一動點,四邊形PQMN為內接矩形,請探索:當點P運動到什么位置時,矩形PQMN的面積最大?
2.從一般到特殊
將原命題中的一般三角形改為特殊三角形。
①如圖,已知AB=AC=100,BC=120(刪去AD=80)
②如圖, 已知∠BAC=900,AB=80,AC=60.(刪去BC=120,AD=80)
3.從有限到無限
①若將原命題中的余料△APN按原題方式進行再加工,則其內接正方形的邊長X2是多少?如此一直加工下去,則第n次內接正方形邊長Xn又是多少?
②若將原命題中的一個正方形變成如圖橫放著的兩個正方形PQGF,GFNM或n個正方形,則它的邊長又等于多少呢?
總之,教育是一個“慢活”、“細活”,是生命的潛移默化的過程。一粒種子種在地里,我們要有足夠的耐心,等它生根、發芽、長葉、開花、結果,這是漫長的寂寞的等待過程。我們不能有悖于學生的認知、成長的規律,不能揠苗助長,要放慢教育的速度,留足等待的時間和空間。愿我們提倡的課堂慢教育像春天一樣給孩子們帶來希望,像陽光一樣沐浴著自然、天性的回歸。
【參考文獻】
[1]張文質.《慢教育》(第一輯),華東師范大學出版社出版
[2]《全日制義務教育數學課程標準(修改稿)》.人民教育出版社出版
[3]《教育是慢的藝術》.南方出版社

