余能原理基面力元法在桁架彈塑性分析中的應用

李瑞雪，彭一江

(北京工業大學建筑工程學院，北京 100124)

余能原理基面力元法在桁架彈塑性分析中的應用

李瑞雪，彭一江

(北京工業大學建筑工程學院，北京 100124)

基面力元法(BFEM)是一種新型的有限單元法，是以"基面力"來描述一點的應力狀態。為了編制適用于桁架彈塑性分析的MATLAB基面力元程序，以余能原理基面力元法為基礎，將基面力元法的平面4節點的實體單元模型向桁架單元進行退化，列出了退化桁架單元的柔度矩陣、單元軸力和節點位移的具體表達式，并對其控制方程進行了必要的處理。根據退化的桁架單元模型，采用增量法的思想和線性強化彈塑性模型，以三桿超靜定桁架和復雜靜定桁架為算例進行了計算。將計算結果與大型有限元分析軟件ABAQUS的T2D2計算結果進行了對比分析，發現所用方法與ABAQUS的計算結果高度吻合，進一步驗證了基面力理論的正確性和程序的適用性。

塑性力學；有限單元法；基面力元法；余能原理；桁架；彈塑性分析

有限單元法[1]從正式提出至今已經歷了半個多世紀的發展。在過去的幾十年中，以節點位移作為基本未知量的“位移型有限元”，因其清晰易懂的物理概念率先被發展并得到廣泛應用[2]，它是以最小勢能原理作為理論基礎，而且要求它所采用的離散化結構必須滿足位移協調性。但是隨著日益發展的需要，待解決的問題也越來越多樣化和復雜化。不同的有限元模型，例如基于最小余能原理的平衡元[3]、雜交元[4]、非協調元[5]以及廣義協調元[6]等被一大批學者提出并被研究。因此，針對有限元問題探索具有更簡潔的應力和變形描述體系，建立不依賴網格且收斂性好的新型有限元模型是一些學者所關心的。

2003年，GAO[7]提出了一個描述應力狀態的新概念——“基面力(base force，BF)”,該基面力為一階張量，可以像其他傳統的二階張量一樣來描述一點的應力狀態，其表達公式簡潔，推導方程方便。在高玉臣[8-9]工作的基礎上，彭一江[10]開始了基于基面力概念的新型有限元研究，分別對平面問題、空間問題和彈性大變形問題建立了相應的基面力元模型，并于2009年將該方法簡稱為“基面力元法(BFEM)”[11]。經過近幾年的研究，基面力元法理論已經不斷地應用在許多領域中[11-13]，其相關研究工作也引起了國際同行的關注與研究[14-16]。

本文以余能原理基面力元法為基礎，對平面4節點的實體單元模型[17]進行退化，得到了平面2節點的桁架基面力元模型，推導了其柔度矩陣的具體表達式，并進一步對控制方程進行了處理。利用增量法的思想和MATLAB編程語言，編制了桁架的彈塑性基面力元程序，結合典型的平面桁架算例進行了數值計算，驗證了該模型的正確性。

1 桁架單元的基面力元模型

1.1 柔度矩陣

對于平面問題，考慮如圖1所示的平面4節點單元。I，J，K和L分別表示單元4個邊的邊中節點，TI，TJ，TK和TL分別為作用在相應節點上的力，也稱單元面力。

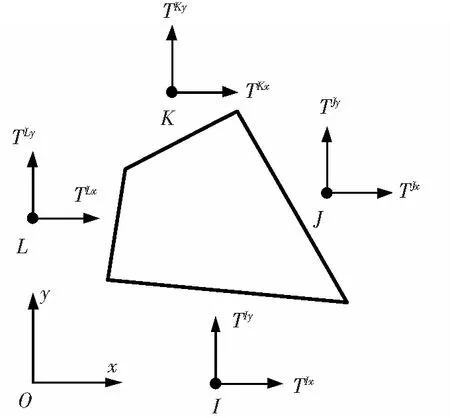
圖1 平面4節點單元Fig.1 Four-node plane element

單元的柔度矩陣可表示為

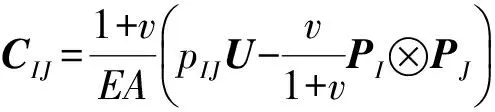
I,J=1,2,3,4。

(1)

退化的平面桁架單元如圖2所示，假設應力均勻的分布在整個桿單元中，α，β分別表示單元的第α節點和第β節點，且α，β=1，2；Tα,Tβ為作用在第α節點和第β節點上的力。

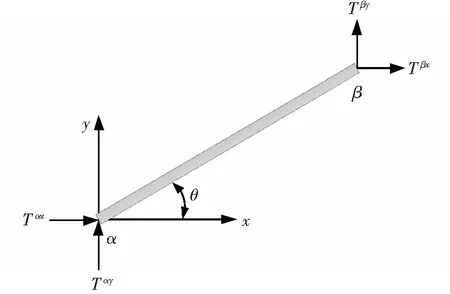
圖2 平面桁架單元Fig.2 Planar truss element

從桁架結構的基本假設上說，不考慮其剪切能力，而泊松比的本質是對剪切效果的研究，所以單純的桁架結構分析不需要泊松比也可以求解出其軸向的力學響應，所以本文假設泊松比v=0，于是桁架單元的余能可寫為

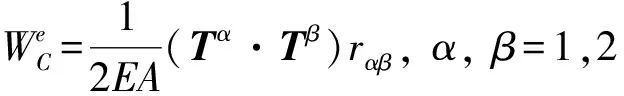
(2)

平面桁架單元的柔度矩陣也可由平面4節點單元退化為

(3)

式中：A為單元的面積；U為單位張量。Pαβ為單元的第α節點和第β節點的徑矢rα和rβ的點積，有

U=ex?ex+ey?ey,

(4)

rαβ=rα·rβ=rαxrβx+rαyrβy。

(5)

最終可以得到Cαβ的具體形式

(6)

1.2 單元軸力表達式

根據文獻[17]，基線力Tα與Cauchy應力張量σ的關系式為

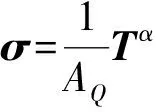
(7)

由于桁架單元中假設只有軸力，且其應力在整個桿中都是均勻分布的，單元的應力可寫為

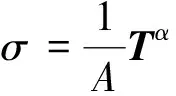
(8)

本文計算軸力的思路一開始是在求出桿端面力后沿著軸線方向合成得到，后來考慮到桁架不存在剪力，推斷其軸力必是沿軸線方向的主應力與橫截面積的乘積，并且驗證了推斷的正確性，所以有

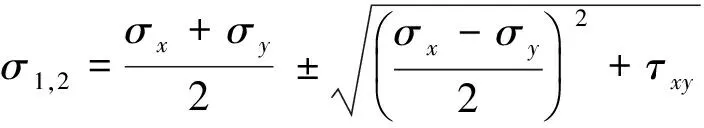
(9)

軸力取不為零的主應力與橫截面積的乘積，有

(10)

式中Acs為桿單元的橫截面面積。

1.3 控制方程及其處理

余能基面力元的控制方程可以寫成

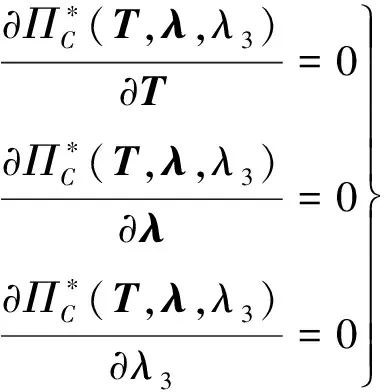
(11)

式(11)的第1式的物理意義是位移協調條件，主要包括：1)不同單元在連接節點處的相對位移為零；2)單元的位移要滿足邊界條件。

式(11)的第2式的物理意義是各單元力的平衡，即每個單元2個節點的力加起來為零。

式(11)的第3式的物理意義是各單元轉動的平衡，即每個單元2個節點的力繞原點的力矩之和為零。

對于之前研究的平面實體單元，每個公共邊界由于只包含2個單元，可由計算機自動判別并賦予兩單元接觸邊上大小相等、方向相反的單元面力T和-T，從而滿足這一約束條件。而對于桁架結構來說，每個公共節點至少包含2個及以上的多個單元，此時未知力的個數也會相應增加，各個未知力不能再簡單設置為等大反向。假如有n個桿交于一點，則需要假設的未知力數是n-1個。

桁架結構的上述特點，導致控制方程與基面力元實體單元主要有兩點不同之處：1)必須考慮各個桿在交點處力的平衡；2)各個桿在交點處的位移協調，即各個桿的相對位移為零。

考慮一個由m個公共節點組成的桿系結構，其部分系統與公共節點i相連的n個桿件及其節點荷載如圖3所示。

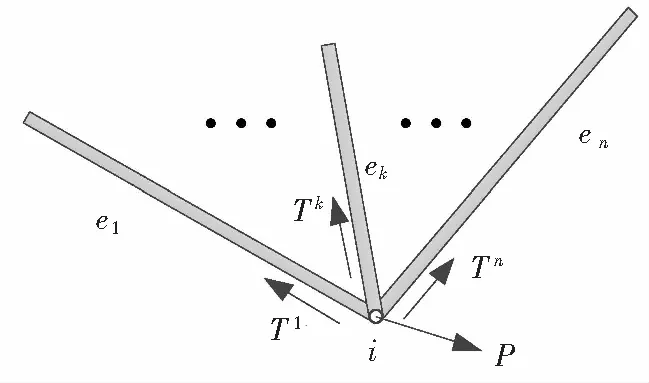
圖3 部分桿系系統Fig.3 Partial rods system

根據交點處力的平衡條件，有

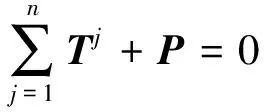
(12)

對于i節點來說，須設有n-1個未知力，第n個桿的力Tn可由其他桿的力來表示，即

Tn=-P-T1-T2-…-Tn-1。

(13)

各桿在交點處的位移協調條件由式(11)的第1式表示，對上述的部分桿系系統可展開為

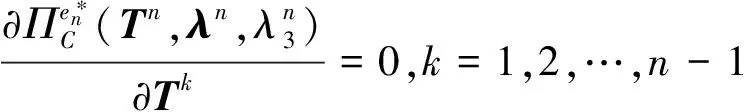
(14)

式(14)表達的物理意義可以理解為第k根桿與第n根桿在相對位移為零，即n根桿是連在一起的。

1.4 節點位移表達式

桁架結構節點I的位移δI可由該點所包含的任意一個單元的支配方程求得，其表達式為

(15)

可得到節點位移δI的顯式表達式

δI=CIJ·TJ+λ+λ3ε·rI。

(16)

其矩陣形式可寫為

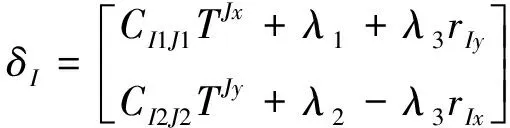
(17)

根據推導的基面力元公式和控制方程，并且采用增量法的思想和線性強化彈塑性模型，編制出了適用于平面桁架彈塑性分析的MATLAB程序。在程序的每一個增量步的計算中，假定方程組是線性的，柔度矩陣也是常數，那么，每步施加一個荷載增量ΔP，得到一個位移增量Δδ，累計后即得到最終的位移。

2 算 例

本文算例采用的材料本構是線性強化彈塑性模型，為研究方便，取各桿的楊氏模型為210GPa，屈服極限為250MPa，并服從Mises屈服條件，屈服后的彈性模量取為42MPa，各桿的橫截面積取單位10cm2。

2.1 三桿超靜定桁架

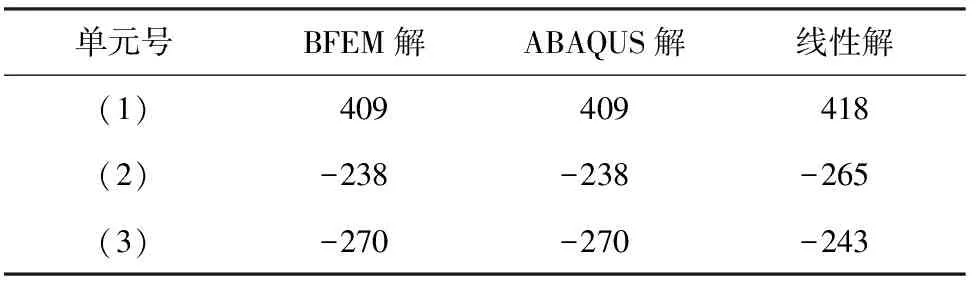
平面三桿超靜定桁架的單元尺寸和所受荷載如圖4所示。將應用本文編制的MATLAB基面力元程序計算該算例，求得的單元軸力解和節點位移解與ABAQUS的計算結果進行對比，并分別列于表1和表2。

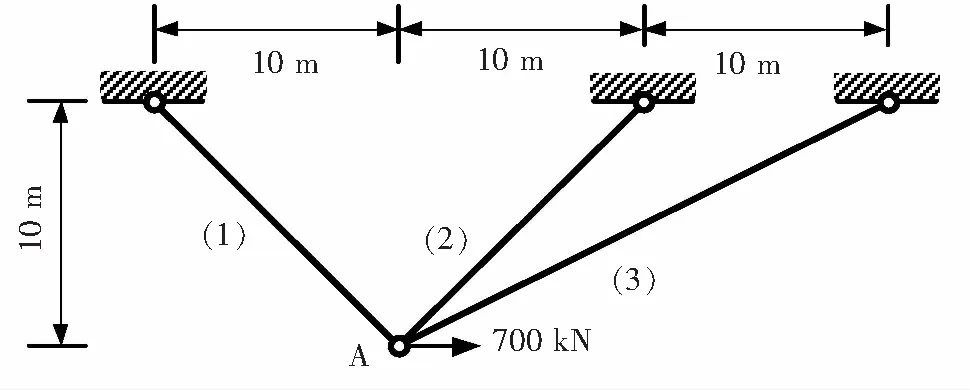
圖4 三桿超靜定桁架的彈塑性分析Fig.4 Elastic-plastic analysis of three bar statically indeterminate truss

kN

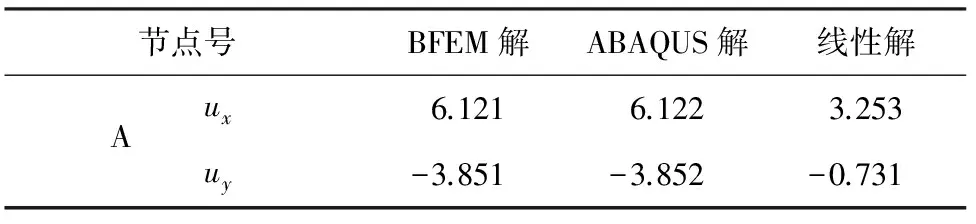
表2 節點位移

從表1中可以看出，(1)單元和(2)單元均率先進入了塑性階段，表2中也可以看出，A點產生了較大的塑性位移。本文對加載后的三桿桁架進行卸載，并將卸載后A節點的位移值與ABAQUS的計算結果對比列于表3。

表3 卸載后的節點位移

最后給出了A點荷載與位移的關系，如圖5所示。

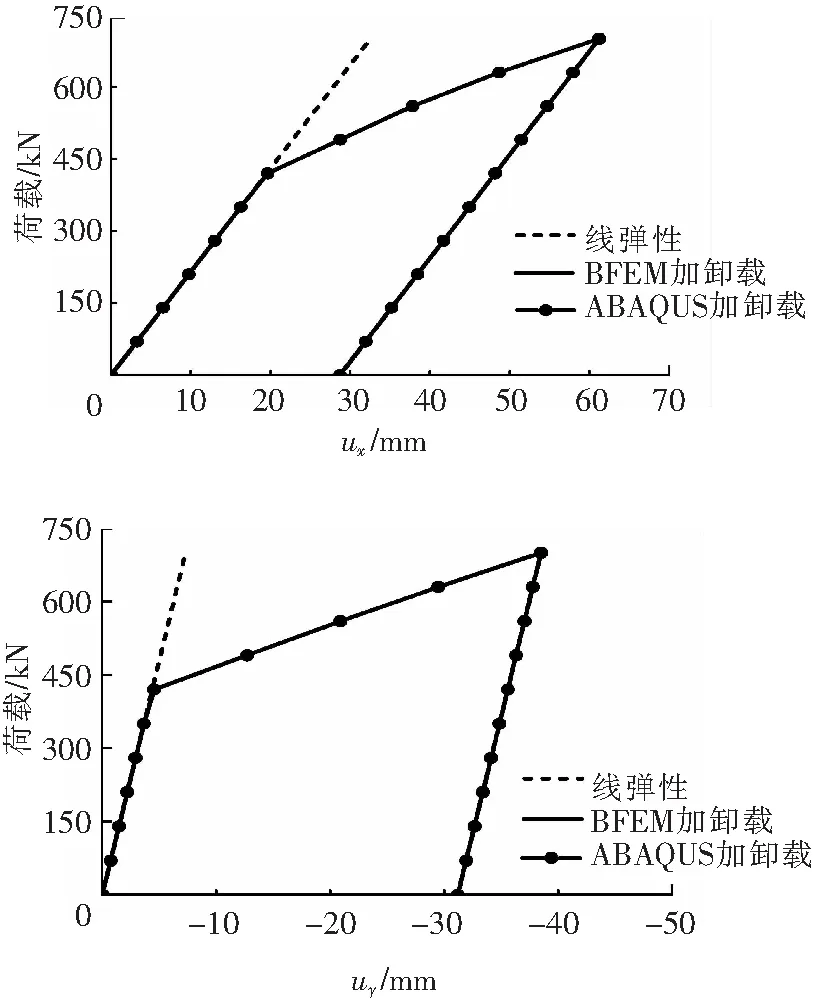
圖5 A點荷載與位移關系曲線Fig.5 Curves between displacement and load at node A

由表1—表3可知，應用彈塑性基面力元程序計算的軸力和位移解與ABAQUS的計算結果高度吻合。荷載和位移的關系曲線圖也比較符合理論情況。

2.2 復雜靜定桁架

平面復雜靜定桁架的單元尺寸和所受荷載如圖6所示。將應用本文編制的MATLAB基面力元程序計算該算例，求得的單元軸力解和節點位移解與ABAQUS的計算結果進行對比，并分別列于表4和表5。

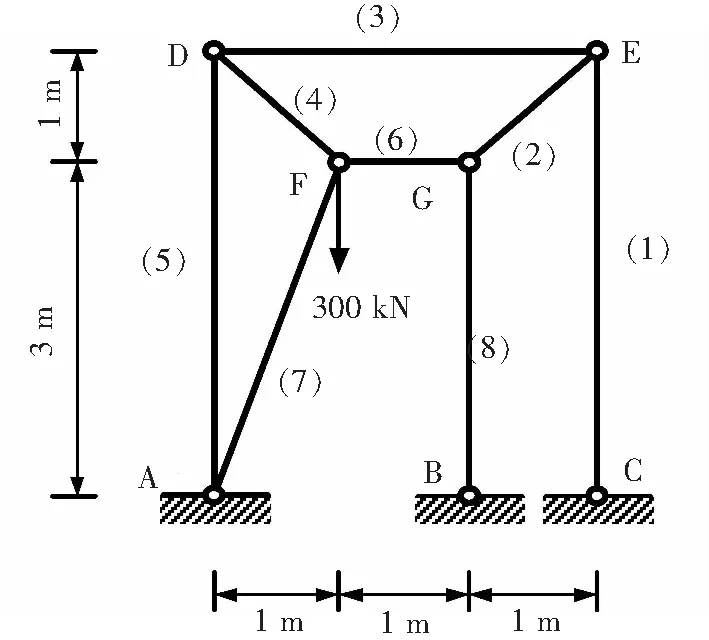
圖6 復雜靜定桁架的彈塑性分析Fig.6 Elastic-plastic analysis of complex statically determinate truss

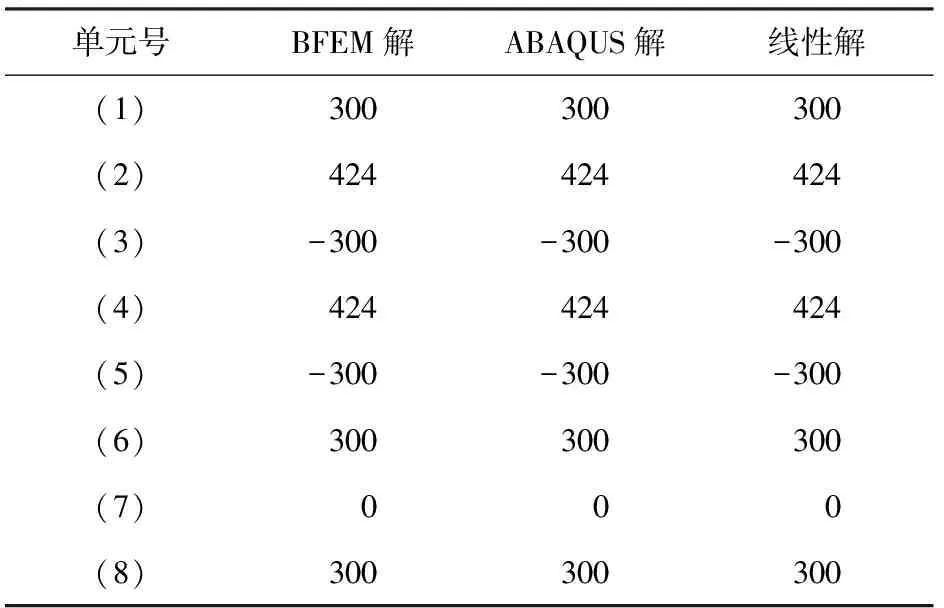
kN

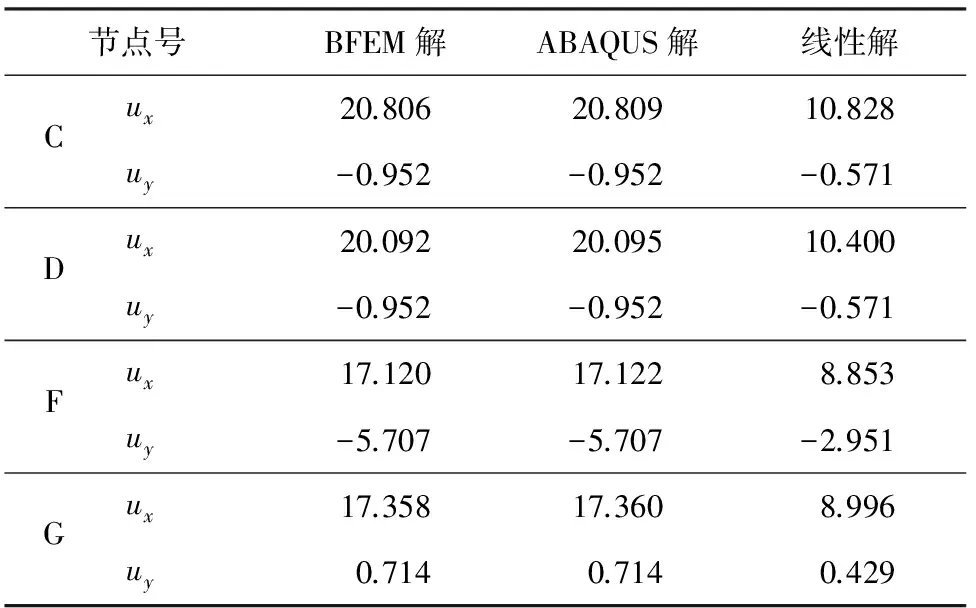
表5 節點位移

對加載后的復雜桁架算例進行卸載，將卸載后各節點的位移值與ABAQUS的計算結果列于表6。

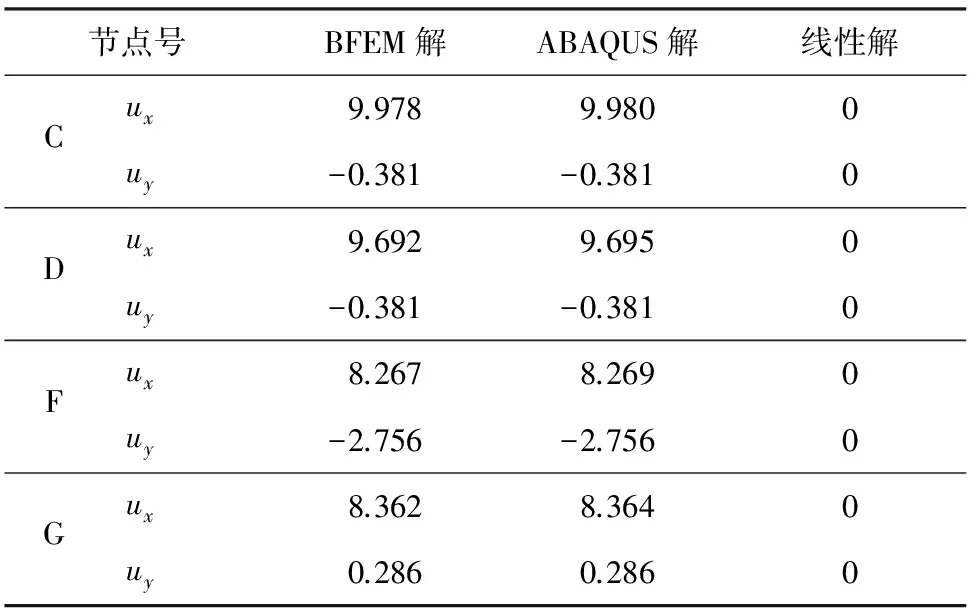
表6 卸載后的節點位移

最后給出了F點荷載與位移的關系，如圖7所示。

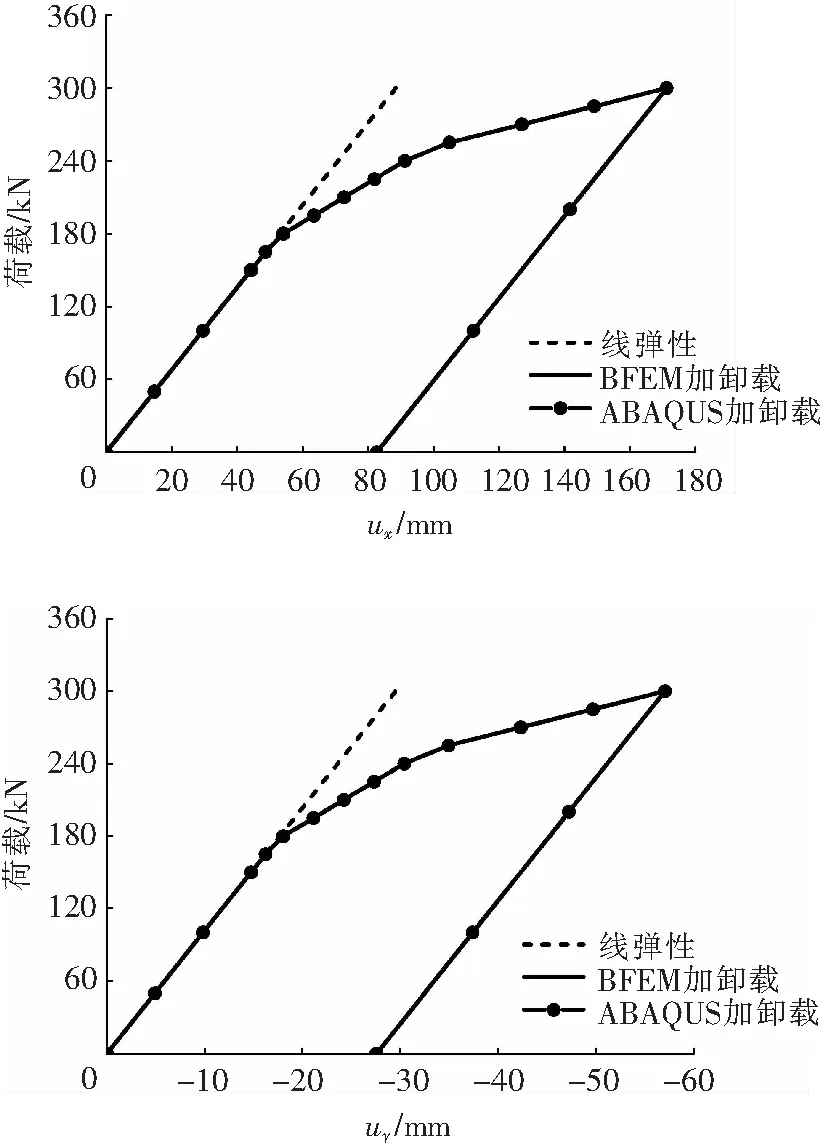
圖7 F點荷載與位移關系曲線Fig.7 Curves between displacement and load at node F

由表4—表6可知，應用彈塑性基面力元程序計算的軸力和位移解與ABAQUS的計算結果高度吻合。荷載和位移的關系曲線圖也比較符合理論情況。

3 結 論

本文把增量法的思想應用于平面桁架單元的余能原理基面力元模型中，編制了能夠對平面桁架進行彈塑性分析的MATLAB程序。與傳統的位移型有限元模型相比，該計算程序誤差較小，具有較高的精度。同時發現，在本文柔度矩陣、軸力以及位移的求解中均不用進行局部坐標系與整體坐標系的轉換。表明以基面力作為基本未知量的桁架基面力元模型的簡潔性和相應程序的適用性，進一步豐富和完善了余能原理在桁架中的應用，同時也表明了基面力元理論的正確性和廣泛的應用前景。

/References:

[1] CLOUGH R W. The finite element method in plane stress analysis[J]. Proceedings of American Society of Civil Engineers, 1960, 23: 345-378.

[2] WASHIZU K. Variational Methods in Elasticity and Plasticity[M]. 2nd ed. New York:Pergamon Press, 1975.

[3] VEUBEKE B F D. Displacement and equilibrium models in the finite element method[J]. International Journal for Numerical Methods in Engineering， 1965, 9(3):145-197.

[4] PIAN T H H,CHEN D P, KANG D. A new formulationof hybrid/mixed finite element[J]. Computers & Structures， 1983, 16(1/2/3/4): 81-87.

[5] WILSON E L, TAYLOR R L, DOHERTY W P, et al. Incompatible displacement models[J]. Numerical and Computer Methods in Structural Mechanics, 1973, 43-57.

[6] 龍馭球.新型有限元論[M].北京：清華大學出版社，2004.

[7] GAO Y C. A new description of the stress state at a point with applications[J].Archive of Applied Mechanics， 2003, 73(3): 171-183.

[8] 高玉臣.固體力學基礎[M].北京：中國鐵道出版社，1999.

[9] 高玉臣.彈性大變形的余能原理[J].中國科學G輯:物理學、力學、天文學， 2006，36(3)：298-311. GAO Yuchen. Complementary energy principle for large elastic deformation[J].Science in China(Series G. Physics, Mechanics & Astronomy, 2006, 36(3): 298-311.

[10]彭一江.基于基面力概念的新型有限元方法[D].北京:北京交通大學,2006. PENG Yijiang. A New Finite Element Method Based on the Concept of Base Force[D]. Beijing: Beijing Jiaotong of Technology, 2006.

[11]PENG Yijiang, LIU Yinghua. Base force element method of complementary energy principle for large rotation problems[J]. Acta Mechanica Sinica, 2009, 25(4): 507-515.

[12]張昭鋒.基于余能原理的基面力元法在巖體力學中的應用[D]. 北京：北京工業大學,2014. ZHANG Zhaofeng. The Application of Base Force Element Method on Complementary Energy Principle in Rock Mechanics[D]. Beijing:Beijing University of Technology, 2014.

[13]王耀.三維基面力元法及其在再生混凝土細觀損傷分析中的應用[D].北京：北京工業大學,2015. WANG Yao. Research of Three-Dimensional Base Force Element Method and Application on Meso-Demage Analysis for Recycled Concrete[D]. Beijing: Beijing University of Technology, 2015.

[14]SANTOS H A F A, PIMENTA P M, ALMEIDA J P M. A hybrid-mixed finite element formulation for the geometrically exact analysis of three-dimensional framed structures[J]. Computational Mechanics,2011, 48: 591-613.

[15]SANTOS H A F A. Variationally consistent force-based finite element for the geometrically non-linear analysis of Euler-Bernoulli framed structures[J]. Finite Elements in Analysis and Design, 2012, 53: 24-36.

[16]SANTOS H A F A. A novel updated Lagrangian complementary energy-based formulation for the elastica problem: force-based finite element model[J]. Acta Mechanica,2015, 226(4): 1133-1151.

[17]彭一江,雷文賢,彭紅濤.基于基線力概念的平面4節點余能有限元模型[J].北京工業大學學報,2009,35(11)：1484-1490. PENG Yijiang, LEI Wenxian, PENG Hongtao. Four-node plane element model on complementary energy based on the concept of base line forces[J]. Journal of Beijing University of Technology, 2009,35(11)：1484-1490.

Application of base force element method with complementary energy principle for elasto-plastic truss analysis

LI Ruixue, PENG Yijiang

(College of Architecture and Civil Engineering, Beijing University of Technology, Beijing 100124, China)

Base force element method(BFEM) is a new type of finite element method, which uses the "base force" as fundamental variables to describe the stress state at a point. In order to compile a base force element program for the elasto-plastic analysis of truss using MATLAB language, based on the BFEM with complementary energy principle, the solid element of the plane 4 nodes in BFEM is degenerated into the truss element. The concrete expressions of the flexibility matrix, axial force and displacement of the degenerated truss elements are derived, and necessary modification of the governing equations is conducted. According to the degenerated truss element model, the idea of incremental method and linear strengthened elasto-plastic model are adopted for calculation by using 3-pole indeterminate truss and complicated static determinacy as samples. It is found that through comparison of the calculated results and the results from T2D2 of ABAQUS, the calculated results using the method are in highly agreement with those obtained with ABAQUS, which further verifies the correctness of the base force element method and the applicability of the program.

plastic mechanics; finite element method; base force element method(BFEM); complementary energy principle; truss; elasto-plastic analysis

1008-1534(2017)04-0276-06

2017-04-07;

2017-04-27；責任編輯：陳書欣

國家自然科學基金(10972015)

李瑞雪(1991—)，男，河北邯鄲人，碩士研究生，主要從事余能原理基面力元法方面的研究。

彭一江教授。E-mail：pengyijiang@bjut.edu.cn

O344

A

10.7535/hbgykj.2017yx04008

李瑞雪，彭一江.余能原理基面力元法在桁架彈塑性分析中的應用[J].河北工業科技,2017,34(4):276-281. LI Ruixue, PENG Yijiang.Application of base force element method with complementary energy principle for elasto-plastic truss analysis[J].Hebei Journal of Industrial Science and Technology,2017,34(4):277-281.