基于半波真有效值的觸/漏電故障電流檢測

左金威, 趙 恒， 陳重佑，肖先勇

(1.四川大學電氣信息學院, 四川 成都 610065；2.電子科技大學，四川 成都 610054)

基于半波真有效值的觸/漏電故障電流檢測

左金威1, 趙 恒1， 陳重佑2，肖先勇1

(1.四川大學電氣信息學院, 四川 成都 610065；2.電子科技大學，四川 成都 610054)

針對現有剩余電流保護裝置存在的死區問題，提出了一種基于半波真有效值的故障電流檢測方法。將總剩余電流相鄰的兩個完整周波離散化后等相位點相減，剔除總剩余電流中的正常剩余電流，保留得到故障電流波形。首先利用幅值絕對值累加的方法確定故障發生周波，接著計算故障發生周波之后的半個故障波形的真有效值，從而實現了故障電流有效值的獲取。利用建模仿真以及觸/漏電實驗實測數據對所提出的方法進行了驗證，證明了所提方法具有可靠性好、計算精度較高、有一定的抗噪聲能力、響應時間短以及簡便易行的優點，很適合工程實際應用，對新型剩余電流保護裝置的開發有一定的參考價值。

剩余電流保護技術；故障電流；幅值；真有效值；數字測量技術

0 引 言

電流動作型剩余電流保護裝置(residual current devices, RCDs)，又稱剩余電流動作斷路器(RCCB)，是目前中國應用最多的剩余電流保護裝置，其動作機理是利用低壓供電回路總剩余電流的幅值大小與設定的基準值作比較，當總剩余電流幅值大于基準值時，通過直接激勵脫扣器或者發出機械開閉信號的方式使開關電器斷開。這種保護裝置的動作機理是低壓電網剩余電流保護裝置的基本動作原理[1]。另一種比較常見的則是電流脈沖型剩余電流保護裝置，是利用低圧回路總剩余電流矢量變化量的幅值大小作為動作判據。

由于故障電流與系統本身存在的正常剩余電流之間存在相位差，而且相位差不確定，導致發生故障的時候總的剩余電流幅值或者總剩余電流變化量的幅值不一定會增大，從而使得現有剩余電流保護裝置存在死區。準確檢測出故障電流，以故障電流有效值作為動作判據，實現電流分離型保護，可以有效解決現有剩余電流保護裝置死區的問題。

針對觸/漏電故障電流提取這一問題，國內的一些專家學者給出了自己的解決方法。文獻[2]提出了一種利用特種波形比較的硬件分離人體觸電電流的方法，但是不能說明該特種波形具有普適性。文獻[3-4]提出了利用小波變換的方法分離觸電電流，但是忽略了人體的電容引起的相位變化。文獻[5-6]采用了B-P神經網絡的方法，文獻[7]用到了支持向量機的方法提取人體觸電電流，但是上述兩種方法需要訓練樣本滿足特定要求，樣本需求量大，計算量很大，而且在正常剩余電流發生變化的時候需要重新訓練樣本，不具有保護所需要的實時性和即時性。

以上方法均是通過求得觸電故障波形后進行保護整定，實際上如果能直接計算得到故障電流的有效值就可以達到無死區保護的效果。這里采用了數字信號的處理技術，對總剩余電流的兩個完整周波進行采樣，將總剩余電流兩個完整的離散波形同相位點對應相減，求得故障支路電流的離散波形。利用幅值變化總量整定的方法確定故障發生周波，接著求取故障發生周波之后半個周波的真有效值，即為故障電流的有效值。通過仿真分析以及觸電物理實驗數據分析，顯示了所提方法在含噪聲、實際漏電故障以及實際動物觸電故障等情況下均有較高計算精度，證明了所提方法可靠性高，具有一定抗干擾能力，而且方法原理簡便、響應速度特別快，很適合工程實際應用。

1 現有剩余電流保護裝置存在的問題

現有的剩余電流保護裝置基本上都是采用的鑒幅機制，是以檢測到的總剩余電流幅值或者是總剩余電流變化矢量的幅值作為動作判據。電流動作型剩余電流保護裝置是目前實際應用最多的觸/漏電保護裝置，它的工作原理是低壓電網剩余電流保護裝置的基本動作原理，見圖1所示。

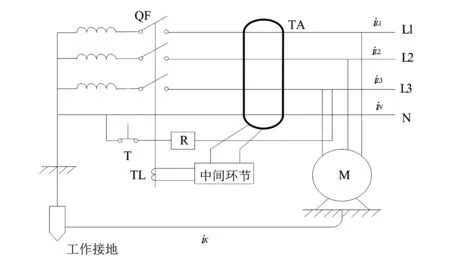
圖1 剩余電流動作型漏電保護器工作原理圖

圖1為三相四線制中性點直接接地系統，三相線路以及零線穿過零序電流互感器一次側的鐵心，在正常情況下，三相線路中的電流iL1、iL2、iL3與零線中流過的電流iN會平衡，剩余電流互感器一次側流過的電流矢量和i為0，鐵心內磁通量也為0 ，零序電流互感器二次回路輸出電壓為0，動作器不動作。當有故障發生時，鐵心包含的導體中的電流矢量平衡會被打破：

iL1+iL2+iL3+iN=i≠0

(1)

由于鐵心內磁通量不再為0，零序電流互感器二次回路會有輸出電壓產生，可以直接激勵脫扣器或者經放大電路后激勵脫扣器脫扣，完成保護動作。

但是，由前面所述可知，由于供電回路絕緣性能不可能絕對良好，即使在系統正常運行情況下，剩余電流互感器一次側流過的電流矢量和i也不是為0，有正常剩余電流i0存在，即正常情況下：

iL1+iL2+iL3+iN=i0=i≠0

(2)

當故障發生時，剩余電流互感器一次側流過的電流矢量和i則是故障電流ir與正常剩余電流i0的矢量和：

i0+ir=i

(3)

ir與i0之間的相位差φ是任意的，假設額定動作電流有效值為Irn，驅動保護裝置動作的故障電流有效值臨界值為Irp，那么保護裝置動作的臨界條件為

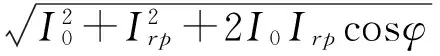
(4)

由式(4)可知，當φ=π時：

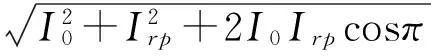
(5)

此時故障電流有效值需要達到正常剩余電流與額定動作電流的有效值之和裝置才能動作，此時裝置最易拒動。

當φ=0時：

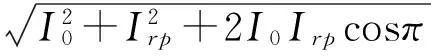
(6)

此時，當故障電流的有效值為額定動作電流與正常剩余電流有效值的差值時裝置就會動作，此時裝置最易誤動或者無法投運。

運行實踐表明，現有剩余電流保護裝置經常會在發生觸/漏電故障的時候無法及時動作；或者是在負荷較大的時候合不上閘而無法正確投運；或者遇到陰雨潮濕天氣時候，由系統絕緣水平顯著下降而誤動作切除電源[5]。

2 基于幅值變化總量的故障周波定位

現有剩余電流保護裝置的保護特性不理想，原因在于其動作電流或多或少受到電網三相不平衡漏電電流的制約。如果能夠從總剩余電流中獲取故障支路汲出電流信號的有效值，以此作為動作判據，就能夠在故障時候準確動作，而不受三相漏電流的影響。

電網在正常運行的時候存在一個正常剩余電流，其構成為基波電流與各整數次諧波電流(主要為3、5、7次諧波，間諧波含量極少，可忽略)的矢量疊加，即使其大小和相位會受到電網運行特性以及天氣等因素的影響，但基本上是一個穩定的周期信號，其基波頻率與電網工頻一致。在故障時候，總剩余電流是正常剩余電流與故障電流的矢量疊加。電網正常剩余電流及故障電流的變化情況如圖2所示。

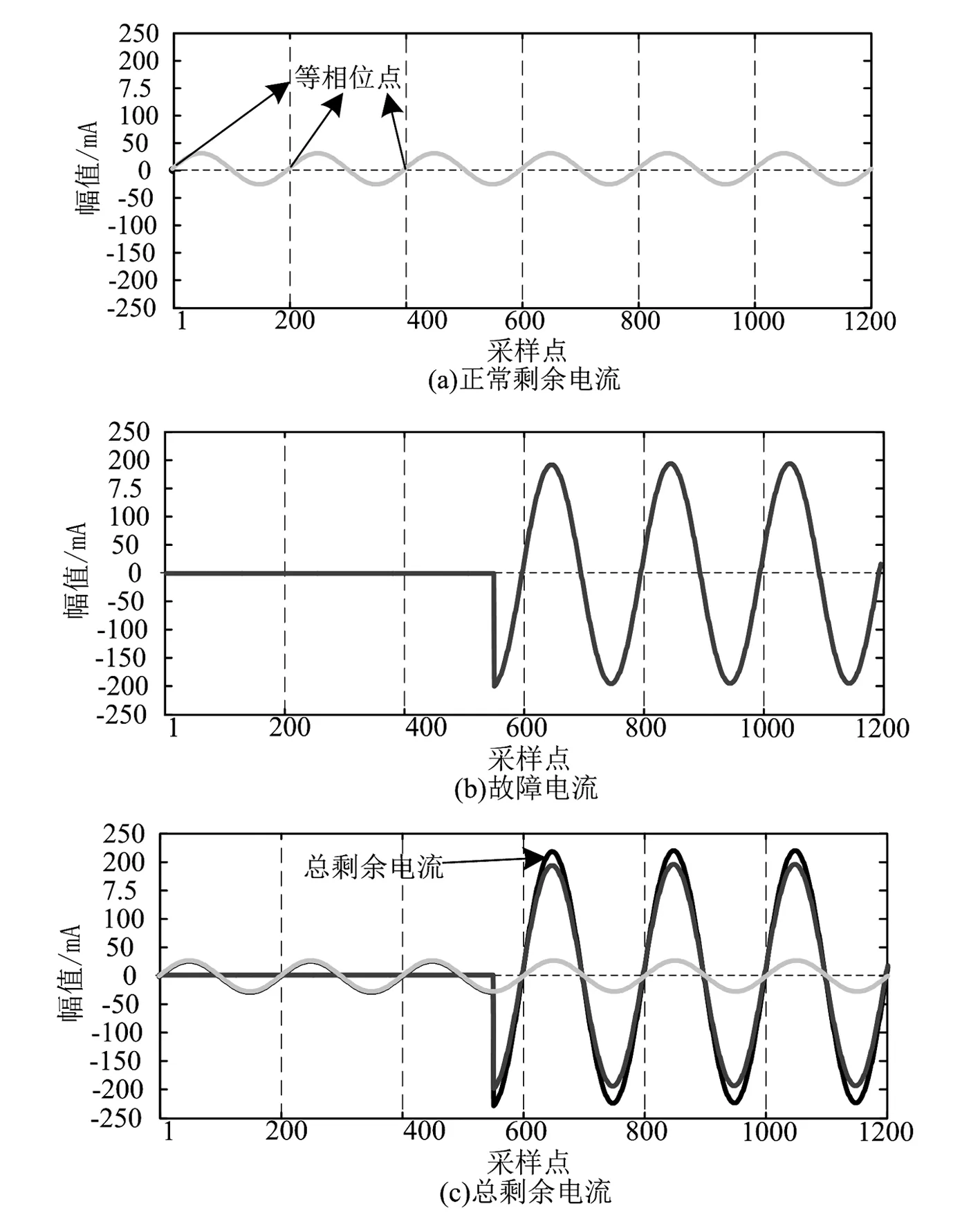
圖2 正常剩余電流及故障電流變化情況

圖2中的波形數據是仿真模擬人體觸電情況得到。電源為有效值220 V的正弦波，工頻50 Hz；正常剩余電流支路阻抗為11 kΩ；故障支路阻抗采用IEC 60990推薦的人體阻抗模型[8]。采樣頻率為10 kHz，每個波形周期采樣200個點，共計6個波形周期1 200個點。

正常剩余電流基波頻率與電力系統頻率一致，中國電力系統的額定頻率為50 Hz，規定頻率偏差范圍為±0.2～±0.5 Hz，在忽略系統噪聲的前提下，可以認為正常剩余電流為幾個頻率穩定的正弦波的矢量疊加。一個正弦波，其同相位點的幅值是相同的，如圖2(a)中所示3個點均為0相位點，采樣點的剩余電流幅值大小也相等，都為0。而整數次諧波的頻率為基波頻率的整數倍，那么基波的等相位點也一定是整數次諧波的等相位點，其等相位點處的采樣值也一定是相等的。總剩余電流i為正常剩余電流ir與故障電流i0的矢量疊加，將總剩余電流相鄰的兩個完整周波等相位處的采樣點對應相減，就可以將正常剩余電流波形抵消掉。各個采樣點的幅值突變量就構成了故障電流的離散波形。具體方法如下：

假設電力系統頻率為f，采樣頻率為fc，每個周波的采樣點數為N，N為正整數。

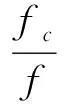
(7)

數據處理窗口一次取總剩余電流i的兩個完整周波作為分析對象，共計2N個采樣點，令第j個采樣點信號為Ij，j=1，2，……，N，Ij采樣點的下一個完整周波的等相位處的采樣點則為Ij+N，那么Ij采樣點的等相位點突變量ΔIj可以表示為

ΔIj=Ij+N-Ij

(8)

ΔIj可以認為是故障電流波形的一個采樣點。相鄰兩個完整周波的采樣點等相位相減以后就可以得到故障電流ir一個周波的離散波形：

ir=(ΔI1,ΔI2,…ΔIj,…ΔIN)

(9)

一個窗口數據處理完畢后，窗口滑動半個周波，即滑動步長為N/2個采樣點，這樣選擇既可以保證有半個波形周期的數據處理時間，也可以保證在最多兩個半波之內確定故障，最重要是能準確識別故障電流。處理方式如圖3所示，此時N為200。步長過短會大大增加數據處理量，如果數據處理不及時就會使得計算結果紊亂；而當滑動步長大于半個周波時會有誤差情況發生，在后面會進一步說明。

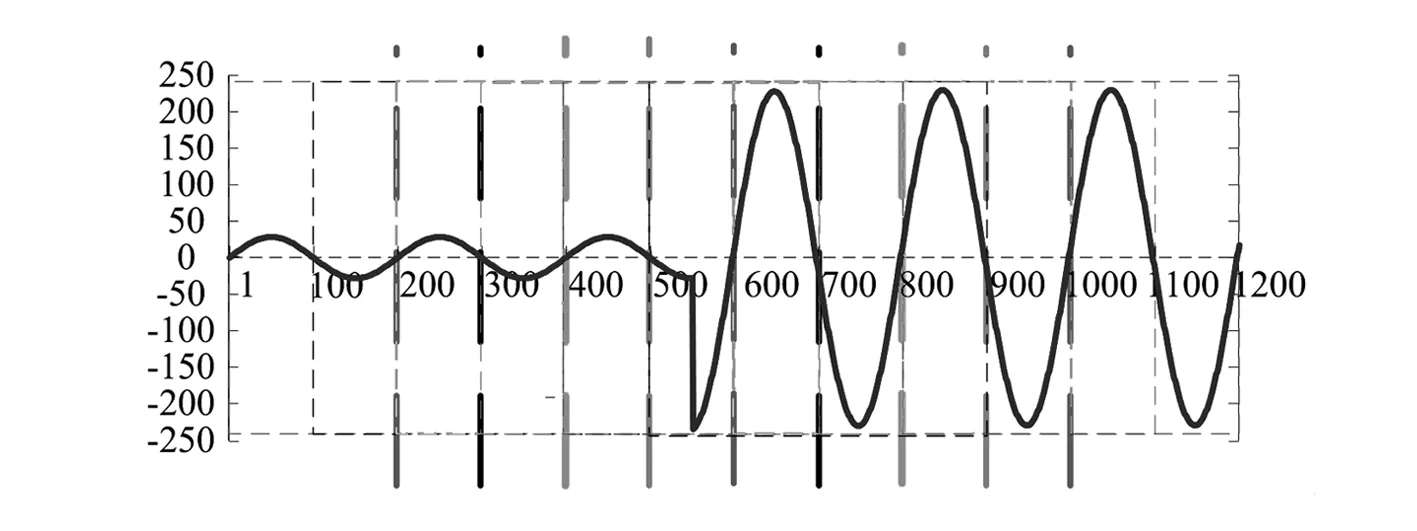
圖3 數據處理窗口示意圖

每個窗口經過這樣的數據處理后就會得到由N個采樣點組成的一個故障電流完整周波的離散波形。而在窗口滑動的過程中，故障波形電流也會在經過數據處理后的結果窗口中以半波N/2個采樣點為步長滑動。結果如圖4所示，此時N為200。

由圖3所示總剩余電流波形的采樣和處理過程中，在前2個窗口，故障尚未發生，處理得到的離散波形也是幾乎為0，如圖4(a)所示；第3個窗口中故障發生，計算得到的故障電流波形也出現，如圖4(b)所示；而在第4個窗口的計算結果中，故障電流波形相比前一個窗口的計算結果向左移動了半個周波100個采樣點，如圖4(c)所示；下一個窗口的計算結果中，故障電流波形依然向左平移半個周波，但是窗口右邊半個周波會被前一個故障周波的等相位半波抵消掉一部分，如圖4(d)所示；直到完全抵消，重新接近于0，如圖4(e)、圖4(f)所示。需要說明的是，由于故障支路阻抗呈容性，故障電流有一個逐漸穩定的過程，所以故障電流抵消的部分并不為0，直到故障電流穩定后才為0，但是這個對計算結果影響很小。

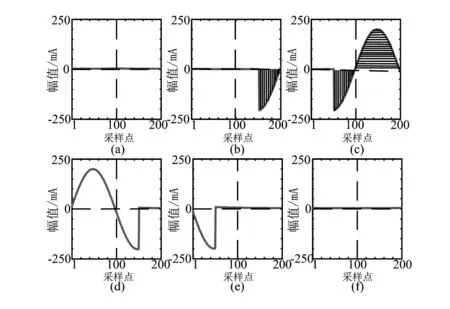
圖4 故障電流波形在結果窗口滑動示意圖

由前面的分析可知，在故障發生時刻所在窗口，計算結果中會有故障電流離散波形出現，可以根據所得離散波形的幅值絕對值的和來確定故障發生的周波。令第T個窗口處理得到的故障電流離散波形為

irT=(ΔIT1,ΔT2,…ΔITj，…ΔITN)

(10)

則其幅值絕對值之和為

(11)

定義故障發生時刻所在窗口判據為

(12)

式中：K為閾值，根據系統噪聲情況以及正常剩余電流大小進行設定；函數值為1表示發生故障，函數值為0表示沒有故障發生。

利用式(8)～式(12)可以確定故障發生時刻所在的窗口。如果故障時刻發生在第T個數據處理窗口，那么第T個窗口中的后一個采樣周波即為故障發生周波，如圖4(b)中陰影部分所示。

3 基于半波真有效值的故障電流整定計算

確定故障發生周波以后，需要進一步計算得到故障電流的有效值，才能進行無死區的剩余電流保護整定工作。在數字測量系統中，交流信號的有效值定義為

(13)

式中：Xeff為被測信號有效值；sqr()代表取平方根；xm(k)為被測信號第m個周波的第k個采樣點；N為交流信號一個周期采樣點。

交流信號有效值的數字測量方法，主要有峰值測量法、平均值測量法和純計算法[9]。前兩種只能計算正弦信號有效值，得不到波形的真有效值[10]。純計算法在滿足奈奎斯特采樣定理[11]并且滿足整周期采樣條件[12](采樣頻率必須為波形頻率的整數倍或有理分數倍)就可以計算得到交流信號的真有效值而不受到諧波的影響。若N為常數或有理分數，只要滿足奈奎斯特采樣定理，式(13)得到的就是真有效值。

電力系統中主要存在的是3、5、7次諧波，故障電流也可以認為是由一個系統頻率的基波與整數次諧波的矢量疊加構成，是一個非正弦的周期信號。非正弦量的有效值等于它的各次諧波有效值平方和的平方根值[9]。一個正弦波的有效值可以用連續的整數個半個周波來進行計算，一個周期信號，基波的連續半個周波一定是包含著整數個的整數次諧波的半個周波(系統中有少量的間諧波，這里忽略不計)，因此含有整數次諧波的故障電流有效值可以利用故障電流連續的半個周波來進行求取。

根據式(7)可知：計算窗口得到的故障電流離散信號滿足整周期采樣條件；忽略系統含量極少的高次諧波，奈奎斯特采樣定理也很容易滿足。因此可以利用純計算法計算故障電流半波的真有效值來確定故障電流的有效值。

假設通過式(8)～式(12),確定了故障發生在第T個數據處理窗，故障電流波形出現。由前面分析可知，在第T+1個結果窗口里故障波形會向左平移半個周波，那么第T+1結果窗口的右邊半個周波一定是故障電流連續的半個周波。如圖4(b)中出現了陰影部分所示的故障電流，那么在接下來圖4(c)所示的結果窗口中，故障電流向左平移了半個周波，右邊半個窗口的波形就是故障周波連續的半個周波，如圖4(c)陰影部分所示。這里可以看出，如果數據處理窗口滑動步長大于半個周波，就會導致圖4(c)所示結果窗口右邊連續的半波有可能被抵消一部分，就會出現誤差。根據式(13)給的交流信號有效值定義，可以計算出第T+1個結果窗口右邊半個周波的故障電流半波真有效值為

(14)

由前面分析可知，由式(14)計算得到的即為故障電流的有效值，可以在故障后發生的兩個半波之內得到結果。

接下來利用以下判據就可以實現無死區的剩余電流保護整定：

(15)

式中，IK為設定的動作電流閾值，函數值為1表示發生故障，函數值為0表示沒有故障發生。

4 仿真數據以及實驗數據驗證分析

下面將通過仿真得到的數據以及實驗室實測數據來驗證上面所述的方法在建模仿真、實際漏電故障以及實際動物觸電故障等情況下的可靠性和精確度。

4.1 數據獲取

利用Matlab搭建模型，仿真模擬人體觸電情況。模型參數：電源為有效值220 V的正弦波，工頻50 Hz；故障支路阻抗采用IEC 60990推薦的人體阻抗模型。改變正常剩余電流支路參數，改變總剩余電流信噪比，每種情況各測得10組樣本數據,編號1～10保存，共獲取60組樣本數據。

搭建物理實驗平臺獲取實際漏電故障情況。實驗參數：市電，正常剩余電流支路參數為12 kΩ電阻與0.47 μF串聯，故障支路參數為15 kΩ電阻。重復實驗10次，共獲取10組樣本數據，編號1～10保存。

利用物理實驗平臺獲取實際動物觸電故障情況。實驗參數為：市電，正常剩余電流支路參數為10 kΩ電阻與0.47 μF串聯，故障支路實驗對象為小兔子。兔子體重2.5 kg，前肢和后肢剃除毛發作為觸電點。重復實驗10次，共獲取10組樣本數據，編號1～10保存。物理實驗平臺如圖5所示。

物理實驗用高精度錄波儀DL750記錄數據。仿真以及物理實驗波形采樣頻率均為10 kHz，每次仿真以及實驗的故障發生時刻隨機，保證故障時刻的故障電流初相位隨機。

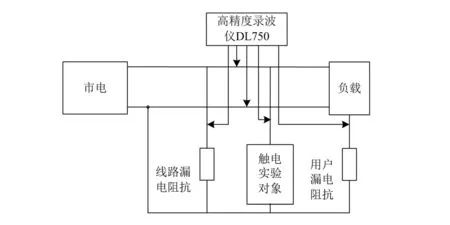
圖5 物理實驗平臺

4.2 數據驗證分析

利用仿真以及實驗所得的數據對所提的基于幅值突變總量的故障周波定位方法進行計算驗證，結果如表1所示。

表1 故障發生周波檢測效果

注：i0為正常剩余電流，i為總剩余電流，與前面一致。

該方法的關鍵在于閾值K的確定，其大小取決于系統噪聲含量以及正常剩余電流大小。由表1可以看出，在噪聲含量較高以及正常剩余電流較大的時候，K也需要取較大值。實際觸/漏電故障實驗中，直接采用220 V市電作為電壓源，系統噪聲以及諧波均自然存在，選取合適的閾值，檢測準確率可以達到100%，證明了所提方法具有一定的抗干擾能力。表1的數據計算表明，在系統正常運行時，只要根據系統情況選取合適的閾值，就能夠保證故障周波的準確定位。方法所需要的計算時間為0.002 1 s，準確性以及響應速度滿足后期檢測要求以及工程實際需求。

確定了故障發生周波之后，進一步利用所獲取的數據對所提的基于半波真有效值的故障電流整定計算方法進行驗證，結果如表2所示。

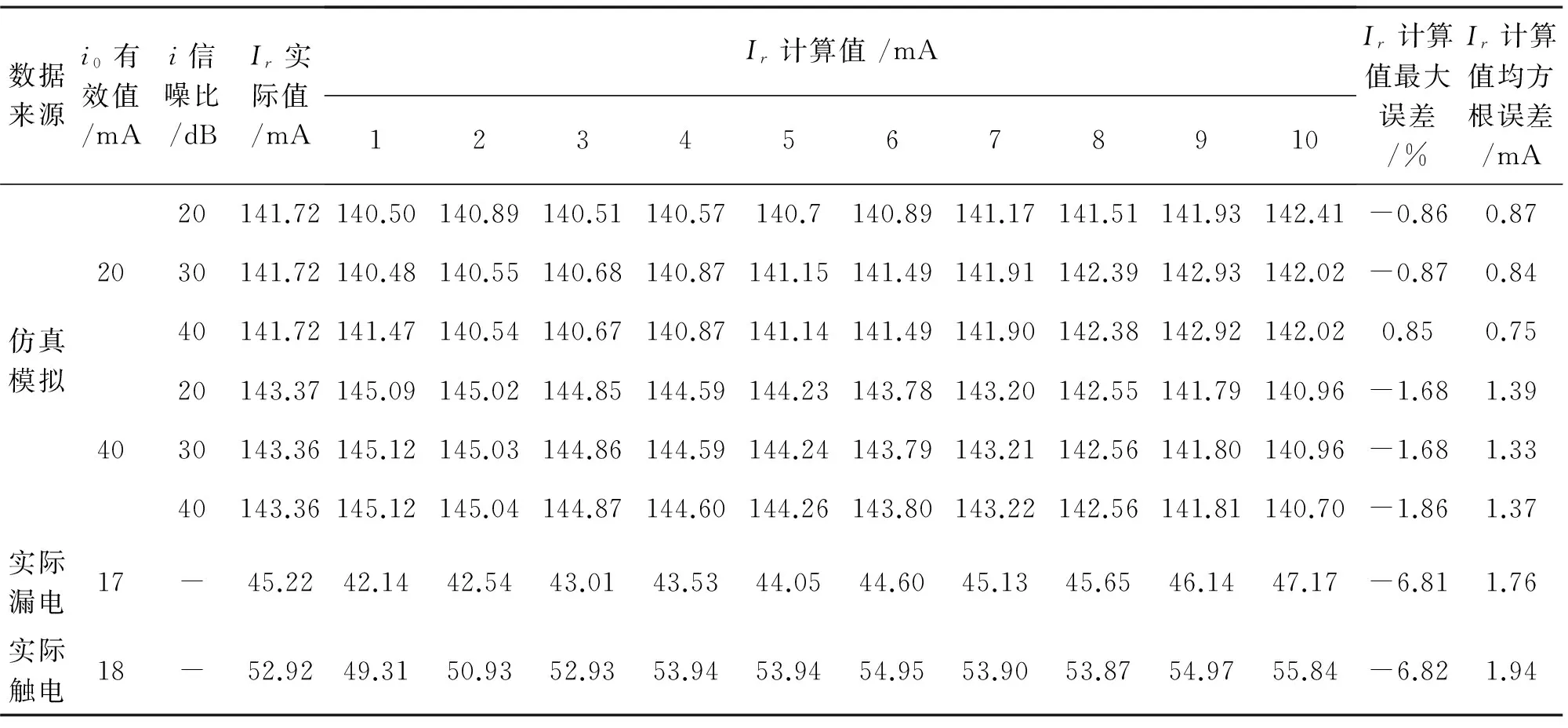
表2 故障電流檢測結果

注：i0為正常剩余電流，i為總剩余電流，Ir為故障電流有效值，與前面一致。由于故障支路并非純阻性，Ir會隨故障的進行略有變化，Ir實際值取故障發生周波的下一個完整周波的有效值。

由表2可知，無論是在仿真模擬的情況下，還是在實際的觸/漏電故障中，所提方法均能夠準確可靠地計算出故障電流的有效值。在仿真模擬情況下，誤差不超過2%；在實際的觸/漏電故障中，誤差不超過10%。均方根誤差(RMSE)是觀測值與真值偏差的平方和觀測次數n比值的平方根，能夠很好地反映出測量的精確度。所提方法，每次仿真或者實驗所得的10組樣本數據的計算值與實際值的均方根誤差不超過2 mA。單次計算時間為0.002 4 s，相較現有方法[14]，計算時間縮短了76%～99%，證明了本方法具有較高的精確度以及較快的響應速度。

由表2還可以看出，正常剩余電流的大小以及系統的噪聲含量會影響計算精度；實際的觸/漏電故障中，系統頻率可能存在±0.2～±0.5 Hz的偏差，系統中存在間諧波，這些因素會影響計算精度。因此，對處理的數據先進行消噪處理可以提高精確度，但是會以更多的計算時間為代價。另外，在保證計算速度并滿足奈奎斯特采樣定律和周期采樣條件的前提下，適當提高采樣頻率，合理設定閾值K，也可以提高最終計算結果的精確度。

5 結 論

1)提出了一種基于幅值變化總量的故障周波定位方法，可以在0.002 1 s的時間內快速確定故障發生的周波。

2)提出了一種基于故障電流半波真有效值的故障電流檢測方法，可以準確快速檢測到觸、漏電故障電流的有效值，單次計算時間為0.002 4 s，相較現有方法，計算時間縮短了76%～99%，方法簡便可靠，響應速度特別快，符合剩余電流保護工程應用領域對實時性的要求。

3)搭建物理實驗平臺，獲取實測數據，證明了所提方法在實際的觸/漏電故障情況下的準確性和可靠性。故障電流有效值計算誤差不超過10%，作為動作判據，能有效消除現有剩余電流保護裝置的動作死區。

[1] 夏越，杜松懷，李春蘭，等. 中國剩余電流保護技術與裝置的發展趨勢[J]. 農業工程學報, 2010, 10, 26(Z2): 151-155.

[2] 滕松林, 楊校生. 觸電漏電保護器及其應用[M]. 北 京: 機械工業出版社, 1994.

[3] 黃俊. 基于小波變換的觸電電流信號檢測方法研究 [D].北京：中國農業大學，2010.

[4] 林軍. 小波變換在零序電流暫態高頻信號分析中的應用[J].電工技術學報，2004，19(4)：89-92.

[5] 李春蘭, 蘇娟, 杜松懷, 等. 基于小波分析和BP神經網絡的觸電信號檢測模型[J].農業工程學報, 2010, 26(Z2): 130-134.

[6] 關海鷗, 杜松懷, 蘇娟, 等.一種觸電信號的自動快速檢測模型[J]. 電網技術, 2013, 37(8): 2328-2335.

[7] 韓曉慧, 杜松懷, 蘇娟, 等. 基于參數優化的最小二乘支持向量機觸電電流檢測方法[J]. 農業工程學報, 2014, 30(23): 238-245.

[8] IEC. Methods of Measurement of Touch Currents and Protective Conductor Current [S]. IEC 60990, 1999-2008(2nd Ed).

[9] 徐墾.交流信號真有效值數字測量方法[J]. 華中科技大學學報(自然科學版), 2006,34 (2): 51-54.

[10] Turner L W. Electronic Engineer′s Reference Book (4th Edition)[M]. London :New aes Butterworths Co. Ltd., 1976.

[11] 胡廣書. 數字信號處理[M]. 北京:清華大學出版社,1997.

[12] Albu M , Heydt G T. On the Use of RMS Values in Power Quality Assessment[J]. IEEE Trans. on Power Delivery, 2003, 18(4):1586-1587.

[13] 熊曉祎， 肖先勇， 趙恒.基于自適應算法的觸電事故 電流檢測[J]. 電力系統保護與控制， 2017, 45(4): 139-144.

Aimed at the problem that the existing protective methods all have protective dead-zones, a method to detect fault current based on the true RMS of the half wave is proposed. After discretization, sampling point subtract the same phase point of total residual current to remove the normal residual current on the total residual current and remain fault current. Firstly, the sum of the absolute values of the amplitude is used to determine the occurrence of the fault current. Then the true RMS value of the half fault waveform is calculated after the fault occurs, thus obtaining the effective value of the fault current. The method can calculate the RMS of the shock/leakage current. The simulation and experimental samples are used for verification. The results show that the method has the advantages of good reliability, high precision, high anti- noise ability, short response time and simple operation. It is very suitable for engineering application, and has a certain reference value for the development of new residual current protection device.

residual current protection technology; fault current; amplitude; true RMS; digital measurement technology

TM74

A

1003-6954(2017)03-0066-07

左金威(1991)，碩士研究生，研究方向為剩余電流保護技術；

2017-05-01)

趙 恒(1983)，博士研究生，研究方向為漏電保護與電氣安全。