船舶交通量的BP神經網絡馬爾科夫預測模型

呂鵬飛+莊元+李洋+楊坤

摘要：為提高船舶交通量的預測精度，在BP神經網絡的基礎上結合馬爾科夫預測模型建立一個新的預測模型.采用通過長江九江大橋的月度船舶交通量數據進行模型訓練、驗證和預測，求出相對殘差值，將相對殘差的前8項歸一化后劃分為3個狀態，利用馬爾科夫預測模型修正BP神經網絡的預測值.該新模型將BP神經網絡的相對殘差值區間從[-12.9%，12.3%]降低至[-9.9%，5.4%].該模型能提高船舶交通量的預測精度，用于預測船舶交通量是可行的.

關鍵詞： 船舶交通量； BP神經網絡； 馬爾科夫預測模型

中圖分類號： U692； TP183； O211.62

文獻標志碼： A

Abstract： To improve prediction accuracy of the ship traffic flow， a new prediction model is established based on BP neural network combined with Markov prediction model. The month data of ship traffic flow crossing the Jiujiang Yangtze River Bridge are used to do the model training， verification and prediction. The relative residuals are calculated， the top 8 relative residuals are divided into 3 states， and Markov prediction model is used to correct the prediction values by BP neural network. The relative residual interval of BP neural network is improved from [-12.9%， 12.3%] to [-9.9%， 5.4%] by the new model， which shows that the new model can improve the prediction accuracy， and is feasible for the prediction of the ship traffic flow.

Key words： ship traffic flow； BP neural network； Markov prediction model

0 引 言

船舶交通量的預測為航道的規劃、設計和船舶通航管理提供基礎性依據[1]，準確預測船舶交通量是海上交通控制和誘導的關鍵.船舶交通量預測模型大多借鑒道路預測模型，其中灰色模型[23]、神經網絡模型[45]、支持向量機模型[68]和組合模型[1，9]是預測船舶交通量常用的模型.

馬爾科夫過程因其無后效性常被用于道路交通量、需水量、用電量、股票等的預測.QI等[10]提出一種隱馬爾科夫模型對高速公路高峰期的交通量進行短期預測.劉宗明等[11]在灰色預測理論的基礎上，對隨機波動大的殘差序列進行馬爾科夫預測.孔垂猛等[12]將建立的灰色馬爾科夫預測模型運用到短時交通量數據的預測中，預測結果較好.景亞平等[13]建立了基于馬爾科夫鏈修正的組合灰色神經網絡城市需水量預測模型，其預測結果優于灰色神經網絡及各單一預測模型的預測結果.何鑫等[14]用馬爾科夫鏈方法預測全國年發電量趨勢.WANG等[15]建立了模糊神經網絡馬爾科夫預測模型預測股票指數.

學者們通常將灰色理論與馬爾科夫鏈相結合以提高船舶交通量預測精度.船舶交通量的大小與天氣、貨運量、海況等因素密切相關，因此船舶交通量的變化趨勢必然不會呈現指數規律.灰色模型適用于具有較強指數規律的序列，只能描述單調的變化過程，并不適用于非單調擺動發展序列或飽和的S形序列.BP（Back Propagation）神經網絡是人工智能網絡中的一個經典模型，因其具有很強的非線性映射能力和自主學習能力備受各行各業研究者的青睞.本文在利用BP神經網絡預測船舶交通量的基礎上，結合馬爾科夫性質對波動較大的預測值序列進行修正，從而提高船舶交通量預測精度.

1 預測模型

1.1 BP神經網絡預測模型

BP神經網絡于1986年由RUMELHART和MCCELLAND提出，是一種按誤差逆傳播算法訓練的多層前饋網絡.神經元是神經網絡的基本單元，是一個多輸入單輸出的非線性原件.神經元輸出值除受輸入值影響外，還受神經元內部因素的影響，因此在神經網絡建模中通常還需設置閾值.對神經網絡進行訓練時，通過不斷調整閾值的大小可以使預測值與實際值的殘差最小，從而提高模型精度.最常用的神經網絡結構包括輸入層（Input layer）、隱層（Hidden

1.3 BP神經網絡馬爾科夫預測模型

BP神經網絡馬爾科夫預測模型的建立步驟：將訓練數據輸入到BP神經網絡預測模型中，計算出預測值與實際值的殘差；利用黃金分割法將相對殘差值劃分為若干狀態后，根據第1.2節馬爾科夫性對預測值進行修正.BP神經網絡馬爾科夫預測模型建立流程見圖2，具體步驟如下.

（1）建立BP神經網絡模型，歸一化原始樣本數據；

（2）用原始樣本數據序列中的前3個數據預測第4個數據，依此類推，得到重組數據后，對其進行訓練、驗證和預測；

（3）將預測值與實際值比較，求出相對殘差值，歸一化后進行狀態劃分；

（4）根據1步狀態轉移頻數求出1步狀態轉移概率矩陣；

（5）根據CK方程求出k步狀態轉移概率矩陣；

（6）用馬爾科夫過程修正BP神經網絡預測結果.

1.4 模型適用范圍

船舶交通量可以理解為單位時間內通過某一水域的船舶實體數，它能夠在一定程度上反映該水域的擁擠程度和危險程度.

它是航運基礎設施建設規劃的主要依據，其預測結果的合理性、準確性、可靠性直接影響投資和效益.通常按照一定的時間跨度對船舶交通量進行預測，一般有短期（短時）、中期和長期預測等3種.任何一種預測模型或方法，都不可能對所有時間跨度的預測全部適用.短期船舶交通量數據具有時間序列非線性的特點，雖然BP神經網絡具有非線性映射能力，可以以任意精度逼近任何非線性連續函數，從而求解內部機制復雜的問題，但是智能程度不高，仍存在許多未解決的問題.同時，馬爾科夫預測模型不擅長處理非線性時間序列.因此，BP神經網絡馬爾科夫預測模型適用于中長期船舶交通量預測.

2 實例驗證及數據分析

以翟久剛等[5]統計的長江九江大橋觀測線月度船舶交通量數據為基礎進行船舶交通量預測.以相鄰前3個數據為訓練樣本預測第4個數據的方法重組33組樣本數據，見表1.取前18組數據作為網絡的訓練數據，后15組數據作為驗證和預測數據.

2.1 BP神經網絡結構及參數設置

設置輸入層神經元數量n=3，輸出層神經元數量l=1，則根據式（2）可得隱層神經元數量m=4，這就構成341的3層神經網絡結構.隱層傳遞函數為tansig，輸出層傳遞函數為purelin，訓練函數為trainlm，學習函數為learngd，訓練次數為5 000次，訓練目標為0.001，學習速率為0.1.

2.2 BP神經網絡預測結果

BP神經網絡預測結果見表2.

2.3 馬爾科夫修正

2.3.1 狀態劃分

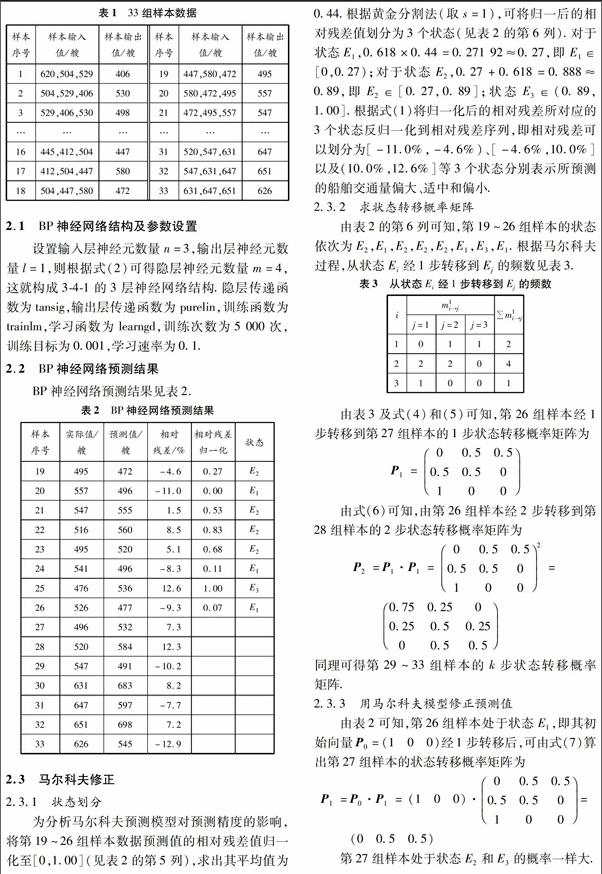
為分析馬爾科夫預測模型對預測精度的影響，將第19～26組樣本數據預測值的相對殘差值歸一化至[0，1.00]（見表2的第5列），求出其平均值為0.44.根據黃金分割法（取s=1），可將歸一后的相對殘差值劃分為3個狀態（見表2的第6列）.對于狀態E1，0.618×0.44=0.271 92≈0.27，即E1∈[0，0.27）；對于狀態E2，0.27+0.618=0.888≈0.89，即E2∈[0.27，0.89]；狀態E3∈（0.89，1.00].根據式（1）將歸一化后的相對殘差所對應的3個狀態反歸一化到相對殘差序列，即相對殘差可以劃分為[-11.0%，-4.6%）、[-4.6%，10.0%]以及（10.0%，12.6%]等3個狀態分別表示所預測的船舶交通量偏大、適中和偏小.

2.3.2 求狀態轉移概率矩陣

由表2的第6列可知，第19～26組樣本的狀態依次為E2，E1，E2，E2，E2，E1，E3，E1.根據馬爾科夫過程，從狀態Ei經1步轉移到Ej的頻數見表3.

第27組樣本處于狀態E2和E3的概率一樣大.根據公式

X=X^/（1-Q）對預測值進行馬爾科夫修正，式中：X^為BP神經網絡預測值，Q為對應的相對殘差區間.由表3可知，第27組樣本的預測值為532，經馬爾科夫模型修正后的預測值區間分別為（480，509）（狀態E2）和（509，592）（狀態E3），則經修正后的預測值取兩區間平均值的平均值后為523.

第28組樣本處于狀態E1的概率最大.由表2可知，第28組樣本的預測值為584，經馬爾科夫模型修正后的預測值區間為（527，559），取平均值后為543.

同理可得第29～33組樣本的預測區間分別為（470，546），（616，654），（571，664），（629，668），（522，606），取各區間的平均值后分別為508，635，618，649，564.經馬爾科夫模型修正后的BP神經網絡預測值見表4.

由表4可知，BP神經網絡預測的月度船舶交通量殘差區間為[-12.9%，12.3%]，經馬爾科夫模型修正后，BP神經網絡預測的月度船舶交通量殘差為[-9.9%，5.4%].經馬爾科夫模型修正后的BP神經網絡預測模型的預測精度優于單一的BP神經網絡預測模型.

3 結束語

船舶交通量的預測精度對確保導航安全、資源的有效利用以及減少水上交通事故的發生具有重要意義.本文提出采用BP神經網絡馬爾科夫預測模型提高船舶交通量的預測精度.實例驗證結果表明，經馬爾科夫模型修正后的BP神經網絡預測的月度船舶交通量殘差區間從[-12.9%，12.3%]降低至[-9.9%，5.4%]，說明經馬爾科夫模型修正后的BP神經網絡預測模型的預測精度優于單一的BP神經網絡預測模型的預測精度.BP神經網絡馬爾科夫模型適用于中長期船舶交通量預測.

參考文獻：

[1]劉敬賢， 張濤， 劉文. 船舶交通流組合預測方法研究[J]. 中國航海， 2009， 32（3）： 8084. DOI： 10.3969/j.issn.10004653.2009.03.018.

[2]張樹奎， 肖英杰. 船舶交通流量預測的灰色神經網絡模型[J]. 上海海事大學學報， 2015， 36（1）： 4649. DOI： 10.13340/j.jsmu.2015.01.008.

[3]馬曉波， 劉雪菲， 戴冉. 優化的長山水道船舶交通流量灰色系統預測模型[J]. 上海海事大學學報， 2016， 37（2）： 1216. DOI： 10.13340/j.jsmu.2016.02.003.

[4]郝勇， 王怡. 基于優化RBF網絡的港口船舶交通流量預測[J]. 中國航海， 2014， 37（2）： 8184. DOI： 10.3969/j.issn.10004653.2014.02.019.

[5]翟久剛， 田延飛， 嚴新平. 基于BP神經網絡與殘差分析的船舶交通流量預測[J]. 上海海事大學學報， 2013， 34（1）： 1922. DOI： 10.3969/j.issn.16729498.2013.01.005.

[6]FENG Hongxiang， KONG Fancun， XIAO Yingjie. Vessel traffic flow forecasting model study based on support vector machine[C]∥Advanced Research on Electronic Commerce， Web Application， and Communication. Berlin Heidelberg： Springer， 2011： 446451. DOI： 10.1007/9783642203671_72.

[7]LI Mingwei， HAN Duanfeng， WANG Wenlong. Vessel traffic flow forecasting by RSVR with chaotic cloud simulated annealing genetic algorithm and KPCA[J]. Neurocomputing， 2015， 157： 243255. DOI： 10.1016/j.neucom.2015.01.010.

[8]馮宏祥， 肖英杰， 孔凡邨. 基于支持向量機的船舶交通流量預測模型[J]. 中國航海， 2011， 34（4）： 6266. DOI： 10.3969/j.issn.10004653.2011.04.014.

[9]李俊， 徐志京， 唐貝貝. 基于GA優化的灰色神經網絡船舶交通流量預測方法研究[J]. 船海工程， 2013， 42（5）： 135137. DOI： 10.3963/j.issn.16717953.2013.05.036.

[10]QI Yan， ISHANK Sherif. A hidden Markov model for short term prediction of traffic conditions on freeways[J]. Transportation Research Part C， 2014， 43： 95111. DOI： 10.1016/j.trc.2014.02.007.

[11]劉宗明， 賈志絢， 李興莉. 基于灰色馬爾科夫鏈模型的交通量預測[J]. 華東交通大學學報， 2012， 29（1）： 3034. DOI： 10.3969/j.issn.10050523.2012.01.007.

[12]孔垂猛， 韓印. 基于灰色馬爾科夫模型的波動性交通流量預測[J]. 森林工程， 2015（1）： 9296. DOI： 10.16270/j.cnki.slgc.2015.01.022.

[13]景亞平， 張鑫， 羅艷. 基于灰色神經網絡與馬爾科夫鏈的城市需水量組合預測[J]. 西北農林科技大學學報（自然科學版）， 2011， 39（7）： 229234. DOI： 10.13207/j.cnki.jnwafu.2011.07.016.

[14]何鑫， 宋平崗， 官二勇. 用馬氏鏈方法預測全國年發電量趨勢[J]. 華東交通大學學報， 2006， 23（4）： 5154. DOI： 10.3969/j.issn.10050523.2006.04.015.

[15]WANG Yifan， CHENG SHihmin， HSU Meihua. Incorporating the Markov chain concept into fuzzy stochastic prediction of stock indexes[J]. Applied Soft Computing， 2010， 10（2）： 613617. DOI： 10.1016/j.asoc.2009.08.028.

[16]高大啟. 有教師的線性基本函數前向三層神經網絡結構研究[J]. 計算機學報， 1998， 21（1）： 8086. DOI： 10.3321/j.issn：02544164.1998.01.011.

[17]FRANK T D. Numeric and exact solutions of the nonlinear ChapmanKolmogorov equation： a case study for a nonlinear semigroup Markov model [J]. International Journal of Modern Physics B， 2009， 23（19）： 36293643. DOI： 10.1142/S0217979209053497.

（編輯 賈裙平）