約束混凝土靶的準靜態柱形空腔膨脹理論

詹昊雯,曹揚悅也,2,蔣志剛,宋殿義,譚清華

(1.國防科學技術大學 指揮軍官基礎教育學院,湖南 長沙 410072;2.代爾夫特理工大學 土木和地球科學學院,荷蘭 2628CN)

約束混凝土靶的準靜態柱形空腔膨脹理論

詹昊雯1,曹揚悅也1,2,蔣志剛1,宋殿義1,譚清華1

(1.國防科學技術大學 指揮軍官基礎教育學院,湖南 長沙 410072;2.代爾夫特理工大學 土木和地球科學學院,荷蘭 2628CN)

針對射彈侵徹約束混凝土靶問題,基于Hoek-Brown(H-B)準則,建立了徑向受彈性約束的有限混凝土介質準靜態柱形空腔膨脹模型,得到了各種響應模式下的擴孔壓力和響應模式轉換條件,分析了擴孔過程以及約束效應對擴孔壓力和侵徹阻力的影響。結果表明:約束混凝土靶的擴孔壓力在擴孔過程中不斷變化,約束剛度對響應模式和擴孔壓力有顯著影響;增大約束剛度可有效提高約束混凝土靶的侵徹阻力,約束混凝土靶的侵徹阻力可比半無限靶提高50%以上。

防護結構;約束混凝土;侵徹;空腔膨脹;H-B準則

由于鋼管對核心混凝土的約束作用,鋼管約束混凝土靶的抗侵徹性能優于普通混凝土靶[1]。硬芯槍彈侵徹試驗[2-4]表明:與半無限混凝土靶相比,鋼管約束混凝土靶的侵徹深度可減小10%～20%,且抗多發打擊性能優良。但是,目前關于約束混凝土抗侵徹問題的理論研究很少,尚無便于工程應用的侵徹阻力計算方法。

基于空腔膨脹理論計算侵徹阻力是研究混凝土侵徹問題的常用方法[5]。Forrestal等[6]發展了無限混凝土介質空腔膨脹理論,并建立了卵形頭剛性彈侵徹半無限混凝土靶的工程模型[7-8]。Li和Chen[9-10]將Forrestal模型推廣到了任意彈頭形狀的剛性彈。黃民榮等[11]建立了基于Griffith準則的空腔膨脹模型,得到了侵徹阻力公式。Warren等[12]基于準靜態球形空腔膨脹模型建立了卵形頭剛性彈侵徹含水飽和混凝土靶的工程模型,理論計算結果與試驗吻合較好。曹揚悅也等[13]考慮混凝土-巖石類靶粉碎區三向受壓特性,基于Hoek-Brown(H-B)非線性強度準則,建立了剛性彈侵徹半無限混凝土-巖石類靶的工程模型。上述模型均針對半無限靶,尚未見到基于空腔膨脹理論的有限尺寸混凝土靶侵徹工程模型。

本文采用H-B準則描述粉碎區混凝土的強度特性,提出了鋼管約束混凝土的準靜態柱形空腔膨脹模型,得到了不同響應模式下的擴孔壓力和轉換條件的解析解,分析了擴孔過程和約束剛度的影響;得到了剛性彈侵徹約束混凝土靶的侵徹阻力計算公式,并與文獻[4]硬芯槍彈侵徹試驗進行了比較,考證了公式的適用性。

1 準靜態有限柱形空腔膨脹模型

1.1 擴孔過程描述與基本方程

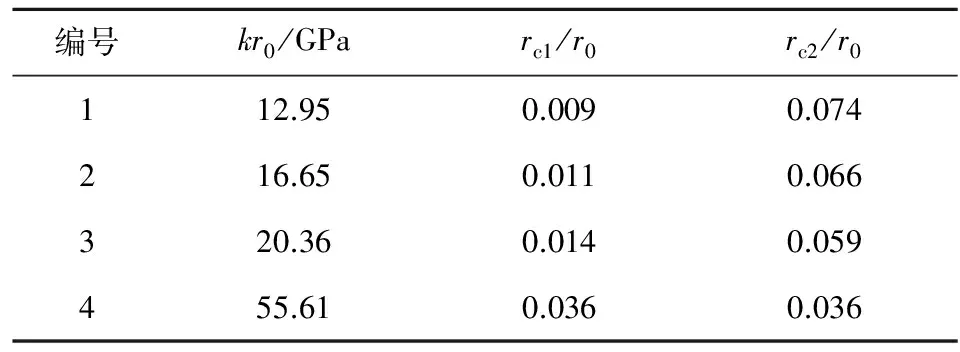
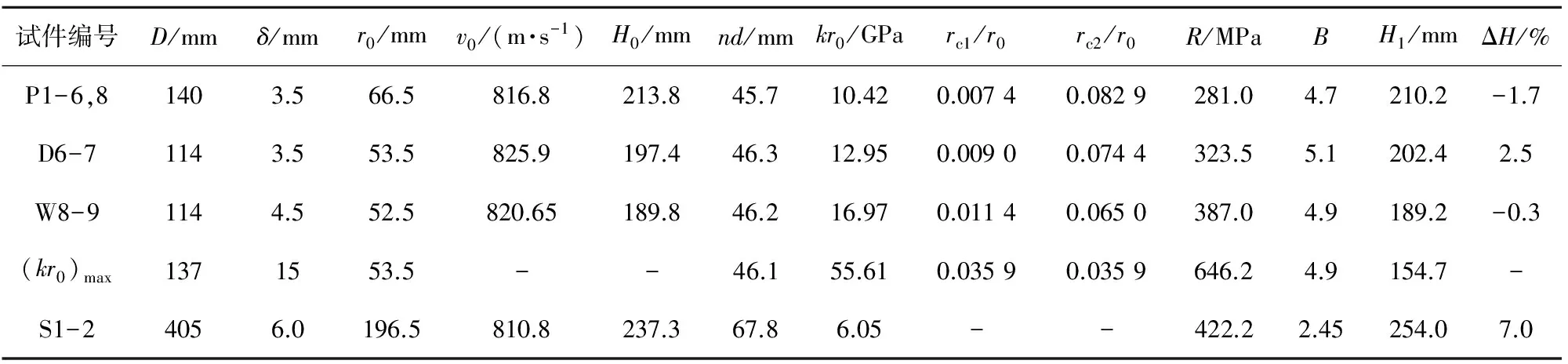
設在受徑向彈性約束、半徑為r0的無限長圓柱形混凝土介質內,有一同軸柱形空腔從半徑為0勻速緩慢地膨脹至半徑rc,彈性波到達混凝土外邊界之前,為無限介質空腔膨脹,空腔外混凝土響應區由外到內依次為未擾動區、彈性區、裂紋區和粉碎區[6];彈性波到達混凝土外邊界之后,即為有限空腔膨脹,徑向約束對擴孔過程產生影響。根據約束剛度的大小,有限空腔膨脹的擴孔過程可能存在以下2種情況:①當約束剛度不夠大、不能限制徑向裂紋的發展時,有限空腔膨脹過程可分為3階段。第一階段為“彈性—裂紋—粉碎”響應,如圖1所示,圖中,k為徑向彈性約束剛度,彈性區半徑re等于核心混凝土半徑r0。隨著空腔半徑的增大,粉碎區和裂紋區不斷向外擴展,彈性區范圍縮小,當裂紋區擴展到核心混凝土外邊界時,彈性區消失,第一階段結束。第二階段為“裂紋—粉碎”響應,粉碎區半徑rp小于裂紋區半徑rcr,且rcr恒等于r0。當粉碎區擴展到核心混凝土外邊界時,第二階段結束。第三階段為“完全粉碎”響應,rp恒等于r0。當徑向約束屈服或破壞時,第三階段結束。②當約束剛度足夠大、徑向約束對核心混凝土施加的徑向壓力足以限制裂紋區的發展時,第一階段的裂紋區可能在尚未擴展到核心混凝土外邊界之前就先于彈性區消失。這種情況下,第一階段“彈性—裂紋—粉碎”響應的結束條件為粉碎區半徑等于裂紋區半徑,且均小于核心混凝土半徑,即rp=rcr

需指出,若粉碎區與裂紋區同時到達核心混凝土外邊界,則上述兩種情況下,均不存在第二階段,直接從第一階段“彈性—裂紋—粉碎”響應轉換為“完全粉碎”響應。由于篇幅有限,本文僅對情況①進行討論,情況②另文討論。

對于準靜態柱形空腔膨脹,采用柱面坐標,各響應區的平衡方程均為

(1)

式中:σr為徑向應力,σθ為環向應力,均以受壓為正;r為空間坐標,以向外為正。

粉碎區混凝土采用H-B準則[13-14]:

(σ1-σ3)2=σu(mσ3+σu)

(2)

式中:σ1,σ3分別為最大、最小主壓應力;σu為單軸抗壓強度;m為無量綱經驗系數[13]。

此外,采用文獻[6]的假定:彈性區為小變形,符合胡克定律,且在與裂紋區交界處環向拉應力達到混凝土單軸抗拉強度σf;裂紋區環向應力為0,且在與粉碎區交界處徑向壓應力達到混凝土單軸抗壓強度σu。

1.2 擴孔壓力求解

1.2.1 彈性—裂紋—粉碎響應

彈性區(rcr

(3)

(4)

式中:E為混凝土彈性模量,ν為泊松比;u為徑向位移,以向外為正。

將式(3)和式(4)代入式(1),求解位移場,并考慮邊界條件(r=r0,σr=ku;r=rcr,σθ=-σf,σf為混凝土單軸抗拉強度),得:

(5)

(6)

(7)

裂紋區(rp

(8)

將式(8)代入式(1),并考慮r=rp處σr=σu和r=rcr處徑向位移連續,得:

(9)

(10)

粉碎區(rc

(11)

代入式(1)得:

(12)

考慮r=rp處徑向應力連續,即σr=σu,解之得:

(13)

令r=rc,σr=σrc,得到求解擴孔壓力的方程:

(14)

式中:rp與rc的關系可以由r=rcr處的徑向應力連續條件和r=rp處的徑向位移連續條件得到。

由式(6)、式(9)和r=rcr處徑向應力連續,得:

(15)

參照文獻[15],忽略粉碎區密度的變化和r=rp處徑向位移up的高階項,由粉碎區質量守恒得:

(16)

考慮r=rp處徑向位移連續,由式(16)和式(10)得:

(17)

聯立式(15)和式(17),可得rp與rc的關系,將其代入式(14),即可求擴孔壓力σrc與rc的關系。順便指出,令r0→∞,kr0→0,可得無限介質空腔膨脹的解。

1.2.2 裂紋—粉碎響應

對于裂紋區(rp

(18)

將式(18)代入式(8),可求得σr。

粉碎區(rc

(19)

由式(14)和式(19),可求擴孔壓力與rc的關系。

1.2.3 完全粉碎響應

式(12)仍然成立。忽略材料密度的變化,由質量守恒,得:

(20)

考慮r=r0處徑向應力σr0=u0k,得:

(21)

積分式(12),并利用邊界條件r=r0,σr=σr0,得到求解擴孔壓力與rc關系的方程:

(22)

1.3 響應模式轉換條件

彈性—裂紋—粉碎響應(第一階段)存在的條件為rp

(23)

綜合約束剛度kr0應滿足條件:

(24)

由式(17)和式(23)可得第一階段末(rcr=r0)的空腔半徑rc1,即:

(25)

裂紋—粉碎響應存在的條件為rc1

(26)

令rp=rcr=r0,由式(15)得kr0=(kr0)max。此時,rc=rc1=rc2,即粉碎區與裂紋區同時到達核心混凝土外邊界,彈性—裂紋—粉碎響應結束,直接進入完全粉碎響應階段。

2 擴孔過程及侵徹阻力分析

參照文獻[4]硬芯槍彈侵徹小直徑鋼管約束混凝土靶試驗,取彈靶參數:彈丸直徑d=12.7mm;彈芯直徑d0=7.5mm,彈芯質量m0=19.7g,彈頭形狀系數N=0.26。混凝土密度ρc=2 140kg/m3,σu=35.8MPa,σf=-3.6MPa,泊松比0.22,彈性模量E=20.25GPa,由式(24)得,(kr0)max=55.61GPa。鋼管彈性模量Es=198GPa。

2.1 擴孔過程分析

取鋼管內半徑r0=53.5mm,壁厚δ=3.5mm,4.5mm和5.5mm,對應的kr0=Esδ/r0[4],rc1/r0,rc2/r0如表1所示,表中kr0=55.61GPa對應的鋼管壁厚δ=15.0mm。

表1 臨界半徑與綜合約束剛度kr0的關系

由表1可知:kr0越大,rc1/r0越大,而rc2/r0越小,即隨著kr0的增大,裂紋區變小;當kr0=55.61 GPa時,rc1/r0=rc2/r0,沒有第二階段。

在H-B準則中取m=15,圖2給出了擴孔壓力與空腔半徑的關系,即擴孔過程。以kr0=16.65 GPa曲線為例,A點對應于無限介質空腔膨脹階段;AB段為第一階段(彈性—裂紋—粉碎響應),B點rc/r0=rc1/r0=0.011;BC段為第二階段(裂紋—粉碎響應),C點rc/r0=rc2/r0=0.066;CD段為第三階段(完全粉粹響應)。

由表1和圖2可知:對于約束混凝土,kr0綜合反映了徑向彈性約束和混凝土自約束效應(外圍混凝土對粉碎區混凝土的約束作用),kr0越大,擴孔壓力越大。當rc/r0

2.2 侵徹阻力分析

根據文獻[2～4],硬芯槍彈侵徹混凝土靶的過程可分為開坑和隧道侵徹2個階段,開坑階段侵徹深度為nd(d為彈丸直徑,n為根據侵徹試驗確定的經驗系數)。基于空腔膨脹理論計算隧道階段的侵徹深度,假設彈頭表面法向壓力σn由靜阻力項和流動阻力項構成,并忽略摩擦力和開坑階段彈芯的速度損失,則侵徹深度公式為

(27)

式中:v0為彈丸撞擊速度;ρc為靶體混凝土密度;R為靜阻力項,B為流動阻力系數。

對于鋼管約束混凝土靶,本文取R為準靜態有限空腔膨脹模型的擴孔壓力σrc(取空腔半徑等于彈芯半徑計算,即rc=d0/2=3.75mm),B根據文獻[4]試驗由式(27)反求得到。按上述方法,表2給出了文獻[4]鋼管約束混凝土靶(P、D、W組)的計算結果。表中:D為鋼管外徑;試驗所得侵徹深度記為H0,式(27)所求侵徹深度記為H1,H1相對于H0的誤差記為ΔH。P、D、W組結果表明,鋼管直徑與壁厚對B的影響不明顯,B可取平均值4.9計算(表中P、D、W組計算H1時,B取4.9)。表2中還給出了(kr0)max和S1-2的計算結果,其中(kr0)max對應于本文適用的最大綜合約束剛度工況,計算中取R=σrc,B=4.9,nd取試驗結果均值46.1mm;S1-2為半無限靶,由于對于槍彈侵徹半無限靶尚無合適的侵徹深度計算公式,因此按文獻[11],取B=2.45,R按文獻[10]中經驗公式R=Sσu計算,其中S=82.6(σu/106)-0.544。

表2 侵徹深度與侵徹阻力計算

由表2可得:

①鋼管約束混凝土靶(P、D、W組)和半無限靶(S1-2)的侵徹深度計算結果與文獻[4]試驗吻合良好,誤差不大于7%。

②鋼管約束混凝土靶的靜阻力隨著約束剛度的增大而增大。當綜合約束剛度較小(kr0≤16.97 GPa)時,由于半無限靶混凝土自約束作用較強,約束混凝土靶的靜阻力小于半無限靶;但當綜合約束剛度較大(kr0=55.61 GPa)時,約束混凝土靶的靜阻力可比半無限靶增大50%以上,侵徹深度可減小約40%。

③鋼管約束混凝土靶的流動阻力系數B約為半無限靶的2倍,即鋼管的約束作用有效約束了混凝土的側向運動,從而增大了動阻力。因此,靜阻力小于半無限靶(綜合約束剛度較小)時,約束混凝土靶的侵徹深度仍小于半無限靶,即鋼管約束混凝土靶的侵徹阻力大于半無限靶。

3 結論

本文首次提出了約束混凝土的準靜態柱形空腔膨脹模型,得到了各響應模式擴孔壓力及模式轉化條件的解析解,分析了擴孔過程和約束效應。結果表明:

①約束混凝土的準靜態擴孔過程與綜合約束剛度有關。當綜合約束剛度較小時,有限空腔膨脹過程分為彈性—裂紋—粉碎、裂紋-粉碎和完全粉碎響應3個階段;當綜合約束剛度達到(kr0)max時,沒有裂紋—粉碎響應直接進入完全粉粹響應。

②綜合約束剛度kr0越大,擴孔壓力越大,侵徹阻力也越大。當kr0較大時,約束混凝土的擴孔壓力始終大于無限介質空腔膨脹。

[1] 蔣志剛,甄明,劉飛,等,鋼管約束混凝土抗侵徹機理的數值模擬[J].振動與沖擊,2015,34(11):1-6. JIANG Zhi-gang,ZHEN Ming,LIU Fei,et al.Simulation of anti-penetration mechanism of steel tube confined concrete[J].Journal of Vibration and Shock,2015,34(11):1-6.(in Chinese)

[2] 甄明,蔣志剛,萬帆,等.鋼管約束混凝土抗侵徹性能試驗[J].國防科技大學學報,2015,37(3):121-127. ZHEN Ming,JIANG Zhi-gang,WAN Fan,et al.Steel tube confined concrete targets penetration experiment[J].Journal of National University of Defense Technology,2015,37(3):121-127.(in Chinese)

[3] 蔣志剛,萬帆,譚清華,等.鋼管約束混凝土抗多發打擊試驗[J].國防科技大學學報,2016,38(3):120-126. JIANG Zhi-gang,WAN Fan,TAN Qing-hua,et al.Multi-hit experiments of steel-tube confined concrete targets[J].Journal of National University of Defense Technology,2016,38(3):120-126.(in Chinese)

[4] WAN Fan,JIANG Zhi-gang,TAN Qing-hua,et al.Response of steel-tube-confined concrete targets to projectile impact[J].Int J Impact Eng,2016,94:50-59.

[5] BEN-DOR G,DUBINSKY A,ELPERIN T.Analytical engineering models for predicting high speed penetration of hard projectiles into concrete shields:a review[J].Int J Damage Mechanics,2015,24(1):76-94.

[6] FORRESTAL M J,TZOU D Y.A spherical cavity-expansion penetration model for concrete targets[J].Int J Solids Struct,1997,34:4 127-4 146.

[7] FORRESTAL M J,ALTMAN B S,CARGILE J D,et al.An empirical equation for penetration depth of ogive-node projectiles into concrete targets[J].Int J Impact Eng,1994,15:395-405.

[8] FORRESTAL M J,FREW D J,HANCHAK S J,et al.Penetration of grout and concrete targets with ogive-nose steel projectiles[J].Int J Impact Eng,1996,18:465-476.

[9] CHEN X W,LI Q M.Deep penetration of a non-deformable projectile with different geometrical characteristics[J].Int J Impact Eng,2002,27:619-637.

[10] LI Q M,CHEN X W.Dimensionless formula for penetration depth of concrete target impacted by a non-deformable projectile[J].Int J Impact Eng,2003,28:93-116.

[11] 黃民榮,顧曉輝,高永宏.基于Griffith強度理論的空腔膨脹模型與應用研究[J].力學與實踐,2009,31(5):30-34. HUANG Min-rong,GU Xiao-hui,GAO Yong-hong.Cavity expansion model based on the Griffith strength theory and its application[J].Mechanics in Engineering,2009,31(5):30-34.(in Chinese)

[12] WARREN T L,FORQUIN P.Penetration of common ordinary strength water saturated concrete targets by rigid ogive-nosed steel projectiles[J].Int J Impact Eng,2016,90:37-45.

[13] 曹揚悅也,蔣志剛,譚清華,等.基于Hoek-Brown準則的混凝土-巖石類靶侵徹模型[J].振動與沖擊,2017,36(5):48-53,60. CAO Yang-yue-ye,JIANG Zhi-gang,TAN Qing-hua,et al.Penetration model for concrete-rock targets based on Hoek-Brown criterion[J].Journal of Vibration and Shock,2017,36(2):7-12.(in Chinese)

[14] HOEK E,BROWN E T.Empirical strength criterion for rock masses[J].Journal of the Geotechnical Engineering Division,1980,9:1 013-35.

[15] SATAPATHY S,BLESS S.Calculation of penetration resistance of brittle materials using spherical cavity expansion analysis[J].Mechanics of Materials,1996,23:323-330.

Quasi-static Cylindrical Cavity-expansion Model for Confined-concrete Targets

ZHAN Hao-wen1,CAO Yang-yue-ye1,2,JIANG Zhi-gang1,SONG Dian-yi1,TAN Qing-hua1

(1.College of Basic Education,National University of Defense Technology,Changsha 410072,China; 2.CITG,Delft University of Technology,Netherland 2628CN)

Aiming at the problem of projectile penetrating into confined concrete target,a quasi-static cylindrical cavity-expansion model for finite concrete target with radially elastic confinement was established based on the Hoek-Brown(H-B)criterion.The pressure at cavity wall and the transition conditions of response modes were obtained.The influence of cavity expansion process and confinement on pressure at cavity wall was also analyzed.The results show that the pressure at cavity wall and resistance of penetration constantly vary during the process of cavity expansion,and the confinement stiffness has significant effect on response modes and pressure at cavity wall.It can greatly improve penetration resistance of confined concrete to increase confinement stiffness.The penetration resistance of confined concrete target is larger than that of semi-infinite concrete target by 50%.

protective structure;confined concrete;penetration;cavity expansion;Hoek-Brown(H-B)criterion

2016-12-02

國家自然科學基金項目(51308539);國防科學技術大學優秀研究生創新資助(S5150901)

詹昊雯(1994- ),女,碩士研究生,研究方向為武器效應與防護。E-mail:283262252@qq.com。

曹揚悅也(1991- ),女,博士研究生,研究方向為計算力學。E-mail:cy3yeah@outlook.com。

TH212;TH213.3

A

1004-499X(2017)02-0013-06