基于二維分岔的超空泡航行體非線性動力學特性分析
呂一品,熊天紅,易文俊,吳錦濤
(南京理工大學 瞬態物理國家重點實驗室,江蘇 南京 210094)
基于二維分岔的超空泡航行體非線性動力學特性分析
呂一品,熊天紅,易文俊,吳錦濤
(南京理工大學 瞬態物理國家重點實驗室,江蘇 南京 210094)
基于二維分岔圖,利用相軌圖、時域仿真圖、Lyapunov指數譜等動力學分析工具分析了超空泡航行體復雜的動力學行為,探討了超空泡航行體運動狀態隨尾翼偏轉角反饋控制增益及空化數的變化規律,確定了航行體穩定運動的條件和參數范圍。結果表明:隨著參數的變化,超空泡航行體的動力學行為中存在分岔、混沌、周期窗等豐富的非線性物理現象;合理調整尾翼偏轉角,能夠有效抑制航行體的振蕩與沖擊。研究結果對超空泡航行體控制器的設計具有重要的指導意義。
超空泡航行體;非線性動力學;二維分岔圖;尾翼偏轉角;空化數
超空泡是由氣泡形成的、幾乎能完全包繞水下運動物體的氣穴空腔。當水下航行體與周圍水體之間發生高速相對運動時,由于靜壓力急速下降,航行體表面附近發生空化,迅速形成覆蓋航行體大部分甚至全部表面的超空泡,大大降低了航行體的阻力系數,提高了航行體的運動速度和距離[1-3]。然而,航行體在水下高速航行時,浮力主要作用在與水接觸的頭部空化器和尾翼上,空化器和尾翼的偏轉角影響超空泡的尺寸及阻力的大小,進而影響航行體運動的穩定性。同時,尾部與空泡壁接觸時會產生復雜的非線性滑行力,滑行力將導致航行體在運動過程中產生有害的振動、沖擊、甚至混沌振蕩等非線性動力學現象[4-5]。
為了有效控制超空泡航行體的運動姿態,減少航行體與空泡壁碰撞產生的沖擊,國內外學者通常選擇頭部空化器偏轉角和尾翼偏轉角作為反饋控制律來保證航行體在水下的穩定運動[6-8]。然而,超空泡航行體的穩定運動受多個系統參數影響,空化數、空化器偏轉角、尾翼偏轉角等參數相互耦合和相互制約,這些系統參數變化所引起的非線性動力學行為是超空泡航行體控制器設計的重要依據。近年來,國內外已有相關研究成果發表,白濤[9]等為保證水下高速運動體在水中能穩定地高速運動,使用分叉法分析運動體的運動穩定性和穩定運動的空化數取值區域;Lin[10]等研究了當空化數在合適的范圍內變化時超空泡航行體動力學特性的變化規律;文獻[11]中呈現了當空化器偏轉角變化時超空泡系統產生的動力學行為。總體來說,有關尾翼偏轉角的變化對超空泡非線性動力學特性影響的研究不多見。本文將以尾翼偏轉角和空化數為可變參數來探討水下超空泡航行體的非線性動力學特性,為下一步超空泡航行體控制器的設計提供理論研究基礎。
基于超空泡航行體四維動力學模型,利用二維分岔圖呈現了系統隨空化數和尾翼偏轉角反饋控制增益變化所產生的非線性物理現象,通過分岔圖、相軌圖、Lyapunov指數譜等非線性動力學工具,分析空化數與尾翼偏轉角對超空泡航行體非線性動力學特性的影響,并對航行體在不同參數下的運動狀態進行仿真。
1 水下超空泡航行體特性
1.1 空化數的描述
空化數是空泡流的基本相似參數,通過改變空化數的大小可以改變流場的空化狀態,當空化數降到小于起始空化數時,流場就由非空化狀態變為空化狀態,進一步降低空化數,在一定條件下流場就可能由氣泡空化狀態發展為局部附體空泡狀態,繼而發展到超空泡狀態[3]。由此可知,空化數是超空化技術的重要技術指標之一。空化數σ是描述空化起始與狀態的一個無因次參數,其表達式為
(1)
式中:p∞為外壓,pc為空泡內壓,ρ為水的密度,v為航行體在縱平面內頭部空化器的合速度[9]。
1.2 水下超空泡航行體受力分析
超空泡航行體的外形結構及受力分析如圖1所示,航行體為回轉體,頭部為空化器,前部為截頭錐體,中部為柱體,尾部為擴張圍裙式尾翼。
作用在航行體上的力主要有:空化器上的升力Fc、尾翼上的升力Ff、航行體質心位置的重力G,以及滑行力Fp,航行體頭部空化器受力表達式[12]為
(2)
式中:Rn為空化器半徑;αc為航行體的攻角,即空化器偏轉角δc和航行體速度v的夾角;阻力系數Cx=Cx0(1+σ),Cx0=0.82。
同理可得,航行體尾翼所受的升力為[12]
(3)
式中:n為尾翼效率,即尾翼浸入水中的長度與尾翼總長度的比值;αf為尾翼偏轉角δe與航行體速度v的夾角。
當航行體在超空泡的包裹下航行時,由于航行體與空泡的相對位置發生變化,其尾部與空泡壁接觸時會產生復雜的非線性滑行力,從而導致航行體產生振動與沖擊。滑行力表達式[13]為
(4)
式中:Rc為空泡半徑,R為航行體半徑,R′=Rc-R,如圖2所示,h為航行體尾部探出空泡的深度,稱作浸沒深度,其表達式為[13]
(5)
式中:wth=(Rc-R)v/L為臨界分界點,L為航行體長度。由式(5)可知,當|w|>wth時,h>0,尾部穿過空泡浸入了水中,產生了滑行力;|w| 航行體中心線與空泡中心線之間的幾何角為浸沒角α,表達式為[13] (6) 1.3 水下超空泡航行體動力學建模 建模選取的體坐標系原點位于航行體頭部圓盤形空化器頂端面的圓心,x軸與航行體對稱軸重合指向前,z軸垂直x軸指向下。z軸方向的速度是w,v表示縱平面內航行體空化器的合速度,θ為航行體俯仰角,q為體坐標系下的俯仰角速度,航行體深度為z。上述變量有如下關系: (7) 通過分析計算空化器和尾部的流體動力,再考慮航行體的重力就可得到航行體全部外力和力矩,基于剛體動力學理論可以推出[14]: (8) 式中:η為模型平均密度與水密度的比值,C為常量,表達式為C=Cx(Rn/R)2/2;重力G可以簡化為[12] (9) 選取參數η=2,n=0.5,Rn=0.019 1m,R=0.050 8m,L=1.8m。以航行體的深度z、垂直速度w、俯仰角θ和俯仰角速度q為狀態變量,聯立式(7)~式(9),可得到以尾翼偏轉角反饋增益k和空化數σ為可變參數的規范的系統動力學方程式: (10) 式中:a22=0.198 2v(1+σ),a24=0.064vσ+1.064v,a42=-0.171 9v(1+σ),a44=-0.075 6v(1+σ),b21=5.998 7[1+(1/σ)],b22=27.442 8[1+(1/σ)],b41=-7.088 6[1+(1/σ)],b42=-21.913 0[1+(1/σ)],d2=-1.226 6,d4=1.449 2。 基于水下超空泡航行體的四維動力學模型(10),保持其他參數取值不變,以k和σ為可變參數,分析在空化數有效范圍σ∈[0.019 8,0.036 8]內[10],尾翼偏轉角δe的反饋控制增益k對航行體動力學的影響,隨機地選取初始條件,運用Matlab軟件編程,依照Lyapunov穩定性理論[15]將方程的穩定解、周期解、混沌解用不同的顏色表示出來,給出了(σ,k)二維分岔圖。 在(σ,k)相空間上,系統的動力學行為分布情況如圖3所示,水平切面是系統隨空化數σ變化的分岔圖;豎直切面是系統隨尾翼偏轉角控制增益k變化的分岔圖。利用二維分岔圖能夠確定超空泡航行體在不同運動狀態下對應的參數取值范圍。圖中淺灰色部分表示航行體的穩定運動區域,在此區域內任取一點(σ,k),航行體在該點對應參數的作用下能夠實現穩定航行;圖中深灰色部分表示航行體周期運動區域,參數在此范圍內取值時,航行體的運動則會出現周期振蕩;圖中黑色部分表示系統的混沌區域,在此范圍內航行體則會出現劇烈的振動與沖擊,進而傾覆。 當系統由穩定狀態切換到周期狀態時,會引發Hopf分岔[15],所以圖中淺灰色區域與深灰色區域的交界線即穩定狀態與周期狀態的臨界切換線,被稱為Hopf分岔線。相應地,深灰色區域與黑色區域的邊界表示周期狀態與混沌狀態的切換,在此邊界處存在切分岔或倍周期分岔等物理現象。 二維分岔圖較為完整地展現了超空泡系統隨參數變化的動力學分布。可見,σ∈[0.019 8,0.031 08]時,在[-4.726,33.08]范圍內調節k的取值均能夠有效實現超空泡航行體的穩定航行,對其穩定性控制具有指導意義。 由超空泡航行體的受力分析可知,只有滑行力Fp是關于垂直速度w的非線性力,其他都是線性力。復雜的非線性力Fp作用于航行體尾部,往往導致航行體的運動出現振動與沖擊,甚至傾覆。從非線性的角度對超空泡航行體系統進行分析,探討在航行過程中產生的非線性物理現象,可以進一步了解超空泡航行體的運動特性,為其穩定性控制做好準備工作。 目前用于刻畫非線性運動特征的方法通常有相軌圖、分岔圖、Lyapunov指數譜等。相軌圖是系統運動軌跡的記錄,反映出系統狀態的變化情況,是觀察系統中動力學行為的最直接的方法[15]。分岔圖是當系統參數變化時,其龐加萊映射在某一坐標軸上的投影,在分岔圖中可以很清晰地描繪出系統性能隨參數變化的特征[15]。李雅普諾夫(Lyapunov)指數沿某一方向取值的正負和大小,表示長時間系統在吸引子中相鄰軌道沿該方向平均發散或收斂的快慢程度[15]。 3.1 空化數對超空泡航行體非線性動力學特性的影響 觀察圖3可以發現,在k=1處作水平切面可以得到同時具有穩定、周期、混沌3種狀態的分岔圖。k=1時,即δe=θ,δc=15z-30θ-0.3q時,系統狀態變量w隨空化數σ變化的分岔情況如圖4所示。 當系統處于小空化數σ∈[0.019 8,0.023 83]時,系統的運動軌跡被吸引到圖中加粗的穩定平衡點上,在此范圍內,求解式(5)和式(10),航行體的垂直速度w總是大于臨界值wth,故浸沒深度h總是大于0,航行體尾部一直處于浸入水中的狀態,由空化器的升力、尾翼的升力以及滑行力共同平衡航行體的重力,使之穩定運動;隨著σ的增加,σ=0.023 83時出現Hopf分岔,此時w=wth=(Rc-R)v/L=2.86 m/s,導致穩定平衡點變成了不穩定平衡點,σ∈[0.023 83,0.031 79]時,航行體平衡態失穩產生周期振蕩;在σ=0.031 82處,出現了一個分岔,形成了周期3軌道,之后一系列倍周期分岔導致σ=0.032 66處出現了混沌現象。圖5是圖4在0.032 5<σ<0.033 0范圍的放大,展示了豐富多樣的分岔行為,σ=0.032 66時,周期3軌道經歷倍周期分岔后合并成一個巨大的混沌吸引子,這種行為被稱為混沌危機[13];在σ=0.032 72處,混沌狀態轉變到周期狀態,發生切分岔,切分岔引起陣發混沌,形成了周期6窗,并在σ=0.032 73處,窗口結束,又突變到混沌狀態。當σ=0.032 77時,系統再由混沌狀態突變到周期軌道,形成了周期5窗,在σ=0.032 79處,窗口結束,次級混沌帶與不穩定的周期軌道相遇,再次引發混沌危機,突變為混沌寬帶。σ=0.032 84時,該混沌寬帶又突變成周期2軌道。由圖4所示,系統在σ=0.033 37處由周期2軌道跳變到周期1軌道,而后沿著該軌道作周期運動。 令k=1,即控制律為δe=θ,δc=15z-30θ-0.3q,選擇σ=0.022,保持航行體其他參數均不變,圖6(a)為此時超空泡航行體的相軌在w-q平面上的投影,狀態變量初始時刻的值較大,在反饋控制律的作用下逐漸被吸引到一個平衡點上,此點為穩定平衡點,系統穩定運動;圖6(b)為隨時間變化的Lyapunov指數譜,4個Lyapunov指數:Ly1=-14.67,Ly2=-15.23,Ly3=-25.63,Ly4=-26.21,均小于0。根據Lyapunov穩定性理論[15],可判斷系統處于穩定狀態。該情況對應于圖3中淺灰色穩定區域的點(0.022,1),同時也驗證了在穩定范圍σ∈[0.019 8,0.023 83]時的分岔分析。 保持k=1,選擇σ=0.030,此時系統軌跡在相平面w-q上的投影為極限環,如圖7(a)所示,這表明系統處于周期振蕩的運動狀態。圖7(b)為相對應的Lyapunov指數譜,Ly1=0.192 3,Ly2=-13.75,Ly3=-16.41,Ly4=-37.51,其中,Ly1近似零值,Ly2,Ly3,Ly4均為負值,根據Lyapunov穩定性理論[15],系統周期振蕩。該情況對應于圖3中深灰色周期區域的點(0.03,1),同時也驗證了在圖4中σ∈[0.023 83,0.031 79]范圍的分岔分析。 保持k=1,選擇σ=0.032 7,系統動力學行為如圖8所示。系統相軌跡在平面w-q上的投影為混沌吸引子,如圖8(a)所示,此時航行體具有復雜的非線性動力學行為。 圖8(b)為對應的Lyapunov指數譜,Ly1=11.1,Ly2=-1.772,Ly3=-24.67,Ly4=-37.75,可以發現,Ly1>0,其他3個Lyapunov指數均小于0,根據Lyapunov穩定性理論[15],系統處于混沌狀態,航行體運動失穩。該情況對應于圖3中黑色混沌區域的點(0.0327,1),同時也驗證了圖4在σ∈[0.032 66,0.032 84]范圍的分岔分析。 3.2 尾翼偏轉角對超空泡航行體非線性動力特性的影響 將空化數σ=0.032 6代入式(10),可得到以尾翼偏轉角反饋控制增益k為可變參數的超空泡航行體動力學方程,基于該方程研究尾翼偏轉角對超空泡航行體非線性動力學的影響。 當σ=0.0326,控制律為δe=kθ,δc=15z-30θ-0.3q時,w隨k變化的分岔情況如圖9所示,表現出了豐富多樣的分岔行為,k∈[-100,-71.5]時,3條穩定的周期軌道說明系統處于周期運動的狀態,接著3條軌道在k=-71.8附近分別發生了分岔,一個形成了周期3軌道,一個沒有形成穩定的運動軌道,另一個形成了周期2軌道,隨著k值的增大,這些軌道在k=-50.5附近均發生分岔,形成了各自的混沌帶,混沌帶在k=-48.1處發生切分岔,形成了2個周期3窗和一個周期1窗,之后在k=-45.9附近由倍周期分岔進入混沌狀態,短暫的混沌狀態結束后,又突變到周期2軌道,當k=-21.2時,周期2軌道發生分岔,一個軌道分岔形成一條穩定的周期軌道,另一條軌道分岔形成2條穩定的周期軌道,這3條軌道在k=-14.6附近發生倍周期分岔并分別形成各自的混沌帶,混沌帶在k=-7.8附近突變到周期2軌道。隨著k的進一步增大,在k=-0.5處,系統由周期狀態進入混沌狀態,當k=0.6時,發生切分岔,形成了周期3窗,之后在k=7.1處突變成混沌狀態,緊接著又回到了周期軌道,直到k=22.6時系統發散。 當σ=0.032 6時,選擇k=5,即系統控制律為δe=5θ,δc=15z-30θ-0.3q,圖10(a)為此時系統的相軌,形成了極限環,航行體的運動處于周期振蕩狀態。圖10(b)為此時對應的Lyapunov指數譜,分別為Ly1=0.216 9,Ly2=-25.84,Ly3=-28.11,Ly4=-31.74,Ly1近似零值,Ly2,Ly3,Ly4均為負值,根據Lyapunov穩定性理論[15],航行體周期振蕩。該情況對應于圖3中黑色周期區域的點(0.032 6,5),同時也驗證了上述分岔分析。 保持σ=0.032 6,令k=7.1,此時系統的相軌圖和Lyapunov指數譜對應于圖11(a)和圖11(b)。 如圖11(a)所示,形成了一個混沌吸引子,航行體的運動具有復雜的非線性動力學行為;如圖11(b)所示,Ly1=10.92,Ly2=-2.29,Ly3=-24.28,Ly4=-38.62,其中Ly1>0,其他3個均小于0,根據Lyapunov穩定性理論[15],系統處于混沌狀態。該情況對應于二維分岔圖中黑色混沌區域的點(0.032 6,7.1),同時也符合上述分岔分析的結果。 由上節的分析討論可知,當空化數σ=0.022,尾翼偏轉角的控制增益k=1時,航行體穩定運動。此時時域響應情況如圖12所示,縱向深度z、垂直速度w、俯仰角θ和俯仰角速度q在控制律的作用下被吸引到平衡點S1(0.080 3,3.336 6,0.038 1,0)上。由式(5)可知,wth=2.82 m/s,如圖12(a)所示,w=3.25 m/s,w>wth,h>0。圖12(c)顯示超空泡航行體尾部伸出空泡長度為0.036 3 m,相應的滑行力Fp=16.68 N,浸沒深度h符合要求,滑行力穩定。此時超空泡航行體在空泡內的位置和姿態固定,頭部的空化器和尾部的滑行力共同維持航行體的平衡,航行體處于小攻角斜向運動的穩定航行狀態。 由上節的分析討論可知,當σ=0.032 6,k=5或σ=0.03,k=1時,系統運動的相軌跡圖均為極限環,航行體均處于周期運動狀態。以σ=0.03,k=1為例,系統各個變量的時域響應情況如圖13所示,縱向深度z、垂直速度w、俯仰角θ和俯仰角速度q以平衡點(0.048 4,1.679 3,0.022 4,0)為中心周期振蕩;浸沒深度h時而等于0,時而突變到0.095 6 m,產生的滑行力Fp在[0,73.64]之間周期振蕩,此現象是由于航行體受重力的影響,尾部下端穿過空泡伸入水中,產生滑行力,接著在滑行力的作用下尾部又被彈回空泡中,如此反復,該現象被稱為“尾擊現象”[13]。由此也表明此時航行體處于周期運動狀態。 由上節的分析討論可知,當σ=0.032 6,k=7.1或σ=0.032 7,k=1時,系統運動的相軌跡圖均為混沌吸引子。以σ=0.032 6,k=7.1為例,時域響應情況如圖14所示,超空泡航行體發射后,狀態變量z,w,θ和q隨著時間變化發生了劇烈的非周期振蕩,航行體的運動將會失穩。由圖14(c)可知,由于“尾擊現象”的出現,h和Fp也在隨時間不斷變化,h最高達到了0.22 m,該長度超過了航行體的直徑,對應的Fp接近200 N,在實際運動中,航行體將失去穩定進而傾覆,因此必須進行有效的控制以避免這種情況發生。 基于二維分岔分析,利用多種非線性動力學分析工具,分析了尾翼偏轉角和空化數對超空泡航行體非線性動力學的影響,得到以下結論:①運用時域仿真、相軌圖、分岔圖等動力學分析工具可以準確地分析超空泡系統在參數影響下的動力學行為;②超空泡航行體的運行軌跡有著復雜的動力學行為,隨著系統參數的變化,出現了混沌、分岔和周期窗等非線性現象;③二維分岔圖能夠確定航行體在不同運動狀態下對應的參數范圍,根據二維分岔圖可以設置合適的控制參數,從而有效控制航行體尾翼的偏轉,實現超空泡航行體的穩定航行,為航行體控制器的設計提供理論研究基礎。 [1] 曹偉,魏英杰,王聰,等.超空泡技術現狀問題與應用[J].力學進展,2006,36(4):571-579. CAO Wei,WEI Ying-jie,WANG Cong,et al.Current status problems and applications of supercavitating technology[J].Advances in Mechanics,2006,36(4):571-579.(in Chinese) [2] 熊天紅,易文俊.高速射彈超空泡減阻試驗研究與數值模擬分析[J].工程力學,2009,26(8):174-178. XIONG Tian-hong,YI Wen-jun.Experimental research and numerical simulation of supercavity drag reduction of a high speed projectile[J].Enggineering Mechanics,2009,26(8):174-178.(in Chinese) [3] 張宇文,袁緒龍,鄧飛.超空泡航行體流體動力學[M].北京:國防工業出版社,2012:3-25. ZHANG Yu-wen,YUAN Xu-long,DENG Fei.Fluid dynamics of supercavitating underwater vehicles[M].Beijing:National Defense Industry Press,2012:3-25.(in Chinese) [4] 魏英杰,王京華,張嘉鐘,等.水下超空泡航行體非線性動力學與控制[J].振動與沖擊,2009,28(6):179-204. WEI Ying-jie,WANG Jing-hua,ZHANG Jia-zhong,et al.Nonlinear dynamics and control of underwater supercavitating vehicle[J].Journal of Vibration and Shock,2009,28(6):179-204.(in Chinese) [5] LIN G J,BALACHANDRAN B,ABED E H.Nonlinear dynamics and bifurcations of a supercavitating vehicle[J].IEEE Journal of Oceanic Engineering,2007,32(4):753-761. [6] VANEK B,BOKOR J,BALAS G J,et al.Longitudinal motion control of a high-speed supercavitation vehicle[J].Journal of Vibration and Control,2006,13(2):159-184. [7] HASSOUNEH M A,NGUYEN V,BALACHANDRAN B,et al.Stability analysis and control of supercavitating vehicles with advection delay[J].Journal of Computational and Nonlinear Dynamics,2012,8(2):233-246. [8] 呂瑞,于開平,魏英杰,等.超空泡航行體的增益自適應變結構控制設計[J].兵工學報,2010,31(3):303-308. LV Rui,YU Kai-ping,WEI Ying-jie,et al.Design of gain adaptivevariable structure controller for supercavitating vehicle[J].Acta Armamentarii,2010,31(3):303-308.(in Chinese) [9] 白濤,孫堯,莫宏偉.分叉分析在水下高速運動體穩定控制中的應用[J].哈爾濱工程大學學報,2008,29(10):1 067-1 075. BAI Tao,SUN Yao,MO Hong-wei.Application of bifurcation analysis to the stability control of underwater high-speed vehicles[J].Journal of Harbin Engineering University,2008,29(10):1 067-1 075.(in Chinese) [10] LIN G J,BALACHANDRAN B,ABED E.Supercavitating body dynamics,bifurcation and control[C]//2005 American Control Conference.USA:IEEE,2005:691-696. [11] 熊天紅,包伯成.超空泡航行體閉環控制動力學特性研究[J].振動與沖擊,2015,34(17):168-173. XIONG Tian-hong,BAO Bo-cheng.Closed-loop control dynamics for supercavitating vehicles[J].Journal of Vibration and Shock,2015,34(17):168-173.(in Chinese) [12] DZIELSKI J,KURDILA A.A benchmark control problem for supercavitating vehicles and an initial investigation of solutions[J].Journal of Vibration and Control,2003,9(7):791-804. [13] LIN G J,BALACHANDRAN B,ABED E H.Bifurcation behavior of a supercavitating vehicle[C]//2006 ASME international Mechanical Engineering Congress and Exposition.USA:ASME 2006:5-10. [14] 白濤,孫堯,莫宏偉.水下高速航行體縱向運動建模及穩定控制[J].中國科技論文在線,2009,4(1):32-38. BAI Tao,SUN Yao,MO Hong-wei.Modeling and stability control of underwater high-speed vehicle[J].Sciencepaper Online,2009,4(1):32-38.(in Chinese) [15] 包伯成.混沌電路導論[M].北京:科學出版社,2013:5-38. BAO Bo-cheng.An introduction to chaotic circuits[M].Beijing:Science Press,2013:5-38.(in Chinese) Nonlinear Dynamic Characteristics of Supercavitating Vehicle Based on Two-dimensional Bifurcation LV Yi-pin,XIONG Tian-hong,YI Wen-jun,WU Jin-tao (National Key Laboratory of Transient Physics,Nanjing University of Science and Technology,Nanjing 210094,China) Based on two-dimensional bifurcation diagram,the complex dynamic behaviors of supercavitating vehicles were analyzed by using dynamic analysis tools,such as phase track diagram,time-domain simulation diagram,Lyapunov exponent spectrum.The motion of supercavitating vehicle changing with feedback control gain of the tail deflection angle and cavitation numbers was explored,and the conditions and ranges of variable parameters for the stable motion of vehicle were determined.The results show that some rich nonlinear phenomena varying with variable parameters,such as bifurcations,period windows and chaos can be found.Vibrations and shocks can be suppressed effectively by reasonably adjusting the tail deflection angle.The research result has an important guiding significance to the design of the controller of supercavitating vehicle. supercavitating vehicle;nonlinear dynamics;two-dimensional bifurcation diagram;tail deflection angle;cavitation number 2017-01-14 國家自然科學基金項目(11402116,11472136);中央高校基本科研業務費專項資金資助(30910612203) 呂一品(1993- ),女,博士研究生,研究方向為超空泡航行體非線性動力學特性與穩定控制研究。E-mail:YipinLv623@126.com。 熊天紅(1977- ),女,講師,博士,研究方向為超空泡減阻技術實驗與理論研究。E-mail:xiongtianhong688@163.com。 TV131.2;O322 A 1004-499X(2017)02-0039-08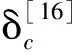
2 水下超空泡航行體的二維分岔分析
3 水下超空泡航行體的非線性動力學
4 超空泡航行體運動特性分析
5 結束語

