一種沖擊波壓力傳感器的準靜態校準神經網絡模型

趙傳榮， 孔德仁， 王勝強， 商 飛

(1.安徽工業大學 電氣與信息工程學院，安徽 馬鞍山 243032； 2.南京理工大學 機械工程學院，南京 210094； 3.西安近代化學研究所，西安 710065)

一種沖擊波壓力傳感器的準靜態校準神經網絡模型

趙傳榮1， 孔德仁2， 王勝強3， 商 飛2

(1.安徽工業大學 電氣與信息工程學院，安徽 馬鞍山 243032； 2.南京理工大學 機械工程學院，南京 210094； 3.西安近代化學研究所，西安 710065)

由沖擊波壓力傳感器準靜態校準原理，間接比對式校準的精度取決于重錘的落高與壓力擬合模型的精度，本文采用RBF神經網絡建立了以落高為輸入量、沖擊波壓力峰值為輸出量的神經網絡模型。選用典型標準壓力傳感器，在7～30 MPa量程范圍開展校準實驗；通過對測試樣本進行分析，結果表明：該神經網絡模型預測的最大相對誤差不超過0.04%，比多項式擬合模型和指數擬合模型高一個數量級。落高與壓力擬合模型引入的不確定度是構成沖擊波壓力傳感器動態測量不確定度的一個重要分量，通過建立高精度的重錘落高與沖擊波壓力峰值神經網絡擬合模型，為進一步提高沖擊波壓力傳感器的測量精度奠定了基礎。

沖擊波壓力傳感器；RBF神經網絡；準靜態校準；擬合模型

沖擊波壓力的大小是評價武器威力的一個重要指標，為定量地評定各類武器或爆炸器材的威力及計算爆炸釋放能量與燃燒率，準確測量沖擊波壓力具有十分重要的意義。

目前常用的壓電式沖擊波壓力測量傳感器，無論是ICP(Integrated Circuit Piezoelectric)型還是高阻抗輸出型，在實際使用中存在以下幾個問題：

(1) ICP型和壓電式高阻輸出的沖擊波壓力傳感器的靈敏度一般都是依靠生產廠家提供的，用戶難以通過標定的手段獲取靈敏度、靜態特性，尤其在使用一段時間后，其靈敏度狀態變化用戶或使用者不甚清楚；

(2) ICP型、高阻抗輸出壓電式傳感器的低頻特性尤其是零頻特性比較差[1]，這是由其工作原理決定的；

(3) 毀傷工況下，其工作環境伴隨著寄生效應，如熱效應、機械沖擊、振動等效應，為準確測量沖擊波壓力，傳感器在工作時必須采取隔熱、防振等技術措施，而采取了這些技術措施后，必然會引起傳感器的等效質量、等效剛度發生變化，導致傳感器的靈敏度發生變化，而由廠家提供的裸傳感器的靈敏度不再適用這種工況下的傳感器組件使用[2-3]。

因此，沖擊波壓力傳感器在使用前，必須對其進行校準。由于壓電式壓力傳感器存在上述諸多問題，采用靜態標定方法會產生靜態漂移等現象，獲得的靈敏度精度不高；基于激波管裝置的動態校準方法，激波管的階躍平臺時間不可能做到無窮大[4-5]，無法反映傳感器測量系統的零頻和低頻特性(一般情況下0～800 Hz或0～1 kHz)，更談不上對沖擊波壓力傳感器實現可溯源的低頻校準。故，目前國內外常用基于落錘式液壓動標裝置的準靜態校準方法[6]對壓電式沖擊波壓力傳感器進行校準。所謂準靜態校準是指用落錘液壓動標裝置產生類似于半正弦型的壓力脈沖對傳感器進行動態校準，壓力脈沖的有效頻帶一般在1 kHz以下，而被校沖擊波壓力傳感器的固有頻率比較高，可達到100 kHz以上，測量系統的可用頻帶比較寬，這對于0～1 kHz低頻段校準來講，相當于準靜態校準。

準靜態校準方法有比對式校準和間接比對式校準兩種[7]，其中比對式校準是直接采用“標準傳感器”與被校傳感器對稱地安裝在基于落錘液壓標定裝置的油缸四周的傳感器安裝孔上，同時監測油缸中的壓力，采用“標準傳感器”直接對被標定的傳感器進行校準。間接比對式校準是當油缸初始容積、活塞有效面積及重錘質量固定不變情況下，對校準用的油缸-重錘組件先用“標準傳感器”進行標定，以獲得沖擊波壓力峰值與重錘落高之間的函數關系，然后拆除“標準傳感器”，利用上述函數關系，由油缸-重錘組件對被標定的傳感器進行校準，實質上是被標傳感器與標準傳感器進行間接比對，這種標定方法對保護壽命較短而價格昂貴的高壓傳感器(“標準傳感器”)是十分有利的，因此它在測試界被廣泛使用。

1 校準方法及試驗設計

落錘液壓動標裝置的工作原理如圖1所示。重錘自由下落撞擊精密活塞組件，活塞組件壓縮造壓油缸內的傳壓介質，產生一個類似于半正弦型壓力脈沖。壓力Pm可通過調節重錘質量m、落高h、活塞桿有效面積S、造壓油缸的初始容積V0等加以改變。

(a)

(b)

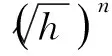
考慮到落錘裝置產生壓力脈沖的影響因素，針對不同的壓力校準范圍，所對應的油缸初始容積、重錘質量及活塞桿有效面積不同。此外，為消除各落高點的壓力隨機誤差，在每點落高處每次安裝都進行n(n≥5)次重復實驗，用這些數據的平均值進行建模。

2 沖擊波壓力傳感器間接比對式準靜態校準神經網絡模型

2.1 RBF神經網絡擬合模型設計

RBF神經網絡具有很強的非線性逼近能力，通過訓練RBF神經網絡能夠以任意精度近似任意非線性函數[11]。與BP神經網絡相比，RBF神經網絡不存在局部最優問題。典型的RBF網絡結構包括輸入層、隱含層和輸出層三層。層與層之間采用全互連方式，同一層單元之間不存在相互連接。隱層節點的基函數對輸入激勵產生一個局部化的響應，輸出節點是隱節點基函數的線性組合。

基于RBF神經網絡建立的沖擊波壓力傳感器間接比對式準靜態校準擬合模型的網絡結構如圖2所示。

逾越節本是游牧民族一年一度的避禍祈福儀式，意思是降災的毀滅者越過了困在埃及的以色列子民的房屋，使各家獲救。逾越節因此有“拯救”之意。見《摩西五經》，馮象譯注，三聯書店，2013年版，第134頁.

第一層為輸入層，只有一個神經元-重錘的落高h。

第二層為隱含層，隱含層節點通過徑向基函數將輸入空間映射到一個新的空間。目前RBF神經網絡常用的基函數為高斯函數。因此，RBF神經網絡隱含層第i個節點的輸出為

圖2 RBF神經網絡結構

(1)

第三層為輸出層，也只有一個神經元-沖擊波壓力峰值Pm，它對隱含層基函數的輸出進行線性加權組合，網絡輸出可表示為

Pm=θ+∑Wiφi

(2)

式中：Wi為隱含層第i個節點與輸出層的連接權值；θ為輸出節點的偏移。

2.2 網絡訓練與驗證

神經網絡結構設計之后，需通過訓練樣本對神經網絡進行學習，網絡中待確定參數有兩類：①基函數中心ci和寬度σi；②輸出層與隱含層之間的連接權值Wi。目前常采用K-均值聚類算法和迭代LMS算法分別學習并確定基函數的中心和寬度，以及輸出層與隱含層之間的連接權值。

3 實驗分析

某落錘液壓動標裝置如圖3所示，“標準傳感器”選用的是四只完全相同的Kistler7005型傳感器，量程0～600 bar。在7～30 MPa壓力范圍的校準實驗數據(即神經網絡學習的訓練樣本)如表1所列，給出的壓力值Pm均是：單個落高獨立重復試驗5次，四只“標準傳感器”監測結果的平均值。為了進一步檢驗模型的精度，給出了表2所示的測試樣本。

圖3 落錘液壓動標裝置

表1 用于7～30 MPa壓力絕對校準建模數據

表2 測試樣本

為了提高網絡的訓練效率，對訓練樣本進行歸一化處理，利用式(3)將表1中數據映射到[0,1]中。

(3)

訓練完后，還需利用式(4)將數據進行還原。

(4)

選擇落高h作為神經網絡的輸入層節點，壓力Pm作為網絡的期望輸出，依據2.1節確定的模型，采用Matlab神經網絡工具箱編制算法程序進行網絡設計、訓練和對訓練后的網絡進行測試。將網絡訓練目標(Goal)(誤差平方和)設置為10-31，在訓練過程中調整擴展因子以趨于正確值，做到誤差最小。網絡訓練結果見圖4。

由圖4可見，實際訓練的誤差平方和為1.265 34×10-32，實際最終使用了9個神經元節點就已經逼近了訓練目標。

最終得出預測效果最好的RBF神經網絡預測模型的參數如表3所列。

圖4 網絡訓練結果

表3 RBF神經網絡參數設置

(5)

其中，剩余標準差為0.087 9 MPa，線性相關系數為0.999 9。

由于表1的實驗數據是在保持重錘質量、造壓油液(傳壓介質)、活塞桿的有效面積以及油缸的初始容積不變的前提下，僅通過改變重錘落高獲得的。根據參考文獻[6]，Pm與h之間的指數擬合關系如式(6)所示。

Pm=2.325 4h0.515 7

(6)

為了驗證構造的神經網絡泛化能力，選取了2個測試樣本來檢驗訓練精度，測試樣本值分別與相應的神經網絡擬合值、多項式擬合值及指數擬合值之間的相對誤差如表4所示。

由表3的對比結果可見，神經網絡模型預測的最大相對誤差不超過0.04%，表明文中所建神經網絡擬合模型的合理與正確。此外，RBF神經網絡擬合值與試驗樣本值更加接近，RBF神經網絡擬合模型的精度比傳統的經驗公式擬合模型精度高一個數量級。

表4 不同方法的計算值

4 結 論

(1) 利用RBF神經網絡能夠以任意精度近似任意非線性函數的特點，建立了以落高為輸入量、壓力峰值為輸出量的神經網絡擬合模型。

(2) 采用測試樣本對建立的重錘落高與沖擊波壓力峰值擬合模型進行檢驗，結果表明，該神經網絡模型預測的最大相對偏差不超過0.04%，四階多項式擬合模型預測的最大相對偏差不超過0.49%，指數擬合模型預測的最大相對偏差不超過0.70%。可見，神經網絡模型的預測精度比傳統經驗擬合公式的精度高一個數量級。

此外，實驗分析神經網絡預測模型的訓練樣本是7～30 MPa壓力范圍的校準實驗數據，因此該神經網絡預測模型的動態壓力校準范圍是7～30 MPa。

[1] XING Qin, ZHANG Jun, QIAN Min. Design, calibration and error analysis of a piezoelectric thrust dynamometer for small thrust liquid pulsed rocket engines[J].Measurement, 2011,44(2):338-344.

[2] 孔德仁, 朱明武, 李永新, 等. 壓力傳感器準靜態“絕對校準”[J]. 傳感器技術，2001, 20(12): 32-34.

KONG Deren, ZHU Mingwu, LI Yongxin, et al. Quasi-static absolute calibration on pressure-measuring sensors[J]. Journal of Transducer Technology, 2001, 20(12): 32-34.

[3] 張玉山, 元虎堂. 壓電式傳感器的準靜態校準[J]. 計量與測試技術, 2009,36(1): 33-34.

ZHANG Yushan, YUAN Hutang. Quasi-static calibration method of piezoelectric transducers[J]. Metrology & Measurement Technique, 2009,36(1): 33-34.

[4] 杜紅棉,祖靜,馬鐵華,等.自由場傳感器外形結構對沖擊波測試的影響研究[J].振動與沖擊,2011,30(11):85-89.

DU Hongmian, ZU Jing, MA Tiehua,et al. Effect of mount configuration of free-field transducers on shock wave measurement[J]. Journal of Vibration ans Shock, 2011, 30(11): 85-89.

[5] 李強, 王中宇, 王卓然, 等. 壓力傳感器激波管校準條件下的動態參數估計[J].北京航空航天大學學報, 2015,41(7):1223-1230.

LI Qiang, WANG Zhongyu, WANG Zhuoran, et al. Dynamic parameter estimation of pressure transducer in shock tube calibration test[J].Journal of Beijing University of Aeronautics and Astronautics,2015, 41(7): 1223-1230.

[6] 孔德仁, 朱明武, 李永新, 等. 量綱分析在傳感器絕對校準建模中的應用[J]. 彈道學報，2002,14(1):93-96.

KONG Deren, ZHU Mingwu, LI Yongxin, et al. The application of dimension analysis on making absolute calibration model of transducers[J]. Journal of Ballistics, 2002,14(1):93-96.

[7] 孔德仁, 朱明武, 李永新, 等. 基于落錘動標裝置的傳感器準靜態絕對校準方法[J]. 南京理工大學學報, 2002, 26(1): 48-51.

KONG Deren, ZHU Mingwu, LI Yongxin, et al. Means of quasi-static absolute calibration of pressure-measuring transducers based on the drop-hammer dynamic pressure calibration system[J]. Journal of Nanjing University of Science and Technology, 2002, 26(1): 48-51.

[8] 朱明武.壓力準靜態校準技術[J].宇航計測技術,2004, 24(2): 19-22.

ZHU Mingwu. Pressure quasi-static calibration technology[J].Journal of Astronautic Metrology and Measurement, 2004, 24(2): 19-22.

[9] 狄長安, 孟祥明, 邊鵬, 等. 高壓壓電傳感器靜態與準靜態校準方法研究[J]. 彈道學報, 2014,26(2): 86-89.

DI Changan, MENG Xiangming, BIAN Peng, et al. Analysis on static and quasi-static sensitivity characteristics of high-pressure piezoelectric sensors[J]. Journal of Ballistics, 2014, 26(2): 86-89.

[10] 王麗, 劉訓濤. 基于神經網絡的壓力傳感器標定技術[J]. 煤炭技術, 2006,25(7): 109-110.

WANG Li, LIU Xuntao. Calibration of pressure sensor based on neural network[J]. Coal Technology, 2006,25(7): 109-110.

[11] 陳明. MATLAB神經網絡原理與實例精解[M]. 北京: 清華大學出版社, 2014.

A neural network model of quasi-static calibration for shock wave pressure sensors

ZHAO Chuanrong1, KONG Deren2, WANG Shengqiang3, SHANG Fei2

1. School of Electrical and Information Engineering, Anhui University of Technology, Ma’anshan 243032, China;2. School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China;3. Xi’an Modern Chemistry Research Institute, Xi’an 710065, China)

According to the principle of quasi-static calibration of shock wave pressure sensors, the indirect comparative calibration accuracy depends on the accuracy of the fitting model for pressure versus height of drop-hammer. Here, the RBF neural network was used to set up a neural network model taking height of drop-hammer as input and shock wave pressure peak as output. Choosing a typical standard pressure sensor, the calibration test was performed in the range of 7-30 MPa. Through analyzing test samples, the results indicated that the maximum relative error of the neural network model’s prediction is not more than 0.04%, the accuracy of this model is one order of magnitude higher than those of the polynomial fitting model and the exponential fitting model; the uncertainty induced by the fitting model for pressure versus height of drop-hammer is an important component of the dynamic measurement uncertainty of shock wave pressure sensors; to build a neural network fitting model for shock wave pressure peak versus height of drop-hammer with a higher accuracy can lay a foundation for improving the measurement accuracy of shock wave pressure sensors.

shock wave pressure sensor; RBF neural network; quasi-static calibration; fitting model

國家自然科學基金(11372143)

2015-11-30 修改稿收到日期：2016-05-11

趙傳榮 男，博士生,1989年生

孔德仁 男，博士，教授，博士生導師，1964年生 E-mail: derenkongnj@sina.com

O385

A

10.13465/j.cnki.jvs.2017.13.014