船舶推進軸系的扭轉-縱向沖擊響應

楊 翼， 王旭榮， 王明坤， 吳 毅， 戴義平

(西安交通大學 能源與動力工程學院，西安 710049)

船舶推進軸系的扭轉-縱向沖擊響應

楊 翼， 王旭榮， 王明坤， 吳 毅， 戴義平

(西安交通大學 能源與動力工程學院，西安 710049)

以某柴油機推進軸系為例，建立了扭轉-縱向沖擊有限元模型，加入柴油機曲軸和螺旋槳附水引起的扭縱耦合效應，研究了扭縱耦合軸系的自由振動和扭轉-縱向沖擊響應，并與無耦合軸系結果進行對比，分析了扭縱耦合效應對推進軸系自由振動和沖擊響應的影響。結果表明，扭縱耦合效應對推進軸系的固有頻率影響不大，但它明顯地影響了沖擊響應，扭縱耦合下，單一類型(扭轉或縱向)沖擊會同時激發縱向和扭轉振動，并且引起較大的位移和扭矩波動，威脅軸系運行安全。因此船舶推進軸系的扭轉-縱向沖擊在設計階段應予以足夠的重視。

船舶推進軸系；沖擊響應；扭縱耦合

船舶在實際航行和作戰中，會受到來自于螺旋槳、主機、海浪等周期或非周期性載荷，以及接觸性爆炸、水中爆炸、空中爆炸、武器發射時反沖造成的沖擊。沖擊應力超過材料的破壞極限會對船舶設備造成嚴重損害，即便沖擊應力低于材料在靜載荷下的強度，但多次沖擊作用會使設備疲勞破壞。推進軸系作為主機與螺旋槳之間傳遞功率和扭矩的核心設備，是保證船舶機動性、安全性和可靠性的關鍵系統[1]，有必要對其沖擊特性進行研究。

國內學者對船舶推進軸系的沖擊響應展開了大量工作。于大鵬等[2-6]通過建立推進軸系的有限元模型，借助有限元軟件或Matlab對推進軸系的沖擊響應進行仿真，分析了軸系沖擊特性及其影響因素。朱小平等[7-8]考慮了梁彎曲振動的幾何非線性，建立船舶推進軸系非線性沖擊動力學仿真模型，并分析了非線性對軸系沖擊的影響。孫洪軍等[9-10]通過實驗的方法對船舶推進軸系沖擊進行研究，并與理論計算結果進行對比，驗證了推進軸系沖擊動力學理論模型的可靠性和適用性。然而，上述研究均局限于船舶推進軸系的橫向和垂向沖擊，對扭轉和縱向沖擊的研究有待深入，張金國等[11-12]分別研究了船舶推進軸系的縱向沖擊和冰載荷沖擊下的扭轉振動響應。實際航行與作戰中，推進軸系會受到各個方向的沖擊，因此對扭轉與縱向沖擊展開研究具有工程實際意義。

另一方面，船舶推進軸系的扭縱耦合振動特性很早就有研究，扭縱耦合效應主要體現在內燃機曲軸和螺旋槳兩部分[13]，一種振動的發生通常伴隨另外一種振動。目前已有的研究主要集中于推進軸系扭縱耦合模型的建立以及扭縱耦合下的自由振動和穩態受迫振動，卻未見有沖擊響應研究。因此，本文以某船舶推進軸系為研究對象，建立了扭轉和縱向沖擊響應計算的有限元模型，考慮了扭縱耦合效應，并分析其對自由振動的影響。最后對扭縱耦合下的沖擊響應進行仿真，并得出了具有一定參考價值的結論。

1 有限元模型

扭轉振動研究中，通常將船舶推進軸系簡化為集總參數模型，由三種基本原件組成：僅考慮轉動慣量的勻質圓盤元件、無慣量阻尼元件和具有扭轉剛度的彈簧元件。而縱向振動研究中，通常將其簡化為由集總質量和彈簧阻尼元件構成的彈簧振子系統。當同時研究縱振和扭振并考慮兩者之間的耦合效應時，應采用牛頓法列寫系統的運動方程。對于大型船舶推進軸系，由于其軸段長，慣性元件多，運動方程數目大，因此采用有限元法建模更加方便。推進軸系的扭縱有限元模型主要由三種原件組成：圓盤元件、推力軸承以及軸段元件。推進軸系的柴油機各缸、飛輪、法蘭和螺旋槳等均簡化為勻質圓盤，其質量和極轉動慣量集中于圓盤中心。每個圓盤均為單節點單元，具有扭轉和縱向兩個自由度，因此其質量矩陣是由圓盤質量m和極轉動慣量J構成的對角陣。推力軸承簡化為油膜剛度、油膜阻尼、軸承座質量和剛度以及船體梁參振質量和剛度。由于上述參數一般很難確定，因此實際計算中，一般簡化為彈簧阻尼單元，一端與推力盤集總質量連接，一端固定[14]。

推進軸段離散為一定數量的兩節點梁單元，如圖1所示，為了和圓盤元件保持協調性，每個節點包含兩個自由度，即縱向自由度u和扭轉自由度θ，因此該梁單元的位移向量可以表示為

(1)

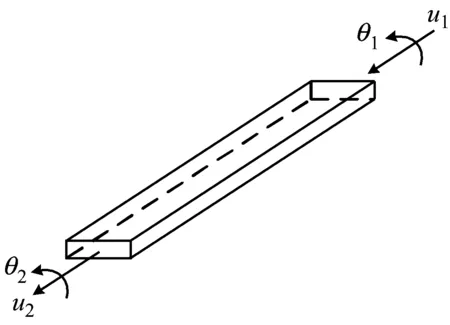
圖1 推進軸的兩節點梁單元

梁單元的質量矩陣和剛度矩陣分別為

(2)

(3)

式中:A為梁的截面積;J為橫截面的扭轉慣性矩;E為彈性模量;G為剪切模量;ρ為密度;L為長度。

得到圓盤、推力軸承和軸段的質量矩陣和剛度矩陣后，即可組裝成推進軸系的非耦合質量矩陣Muc，和非耦合剛度矩陣Kuc。非耦合系統的運動方程可以寫為

(4)

式中:q為系統的廣義位移向量;Cuc為系統的非耦合阻尼矩陣，由軸系的扭轉和縱向阻尼系數確定;f(t)為沖擊載荷向量。

2 扭縱耦合

通過式(2)和式(3)可以明顯看出，軸系的扭轉和縱向自由度相互獨立并不耦合，因此一種振動并不會激發或者影響另一種振動。推進軸系的扭縱耦合效應主要體現在柴油機曲軸和螺旋槳兩部分。

2.1 螺旋槳的扭縱耦合效應

螺旋槳扭縱耦合通常是由螺旋槳附水效應引起的。圖2為螺旋槳軸系的簡化示意圖。圖2中mp為螺旋槳集總質量,Jp為螺旋槳轉動慣量,ku為縱向剛度，kθ為扭轉剛度。

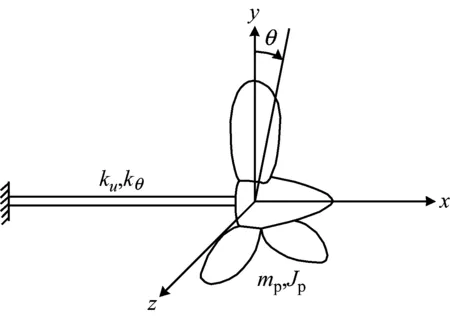
圖2 螺旋槳軸系簡化示意圖

實際中，當螺旋槳在水中轉動時，會產生作用于螺旋槳附水力，該附水力正比于加速度項和速度項，可表示為

(5)

式中:Ma為附水質量矩陣;Ca為螺旋槳阻尼矩陣，可以分別表示為

(6)

(7)

式中:ma為附水質量;Ja為附水轉動慣量；cua為縱向阻尼;cθa為扭轉阻尼；mc為耦合慣性項;cc為耦合阻尼項。這些參數可以按照文獻[15]中的回歸方程求得。

顯然，Ma與Ca的非對角項是引起扭縱耦合振動的因素，當忽略兩個矩陣的非對角項時，不考慮耦合效應的無阻尼自由振動方程為

(8)

式中:m=mp+ma;J=Jp+Ja。

顯然，系統的固有頻率為

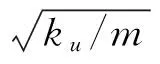
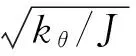
(9)

將Ma的非對角項也即耦合項加入式(8)，可得考慮耦合效應的無阻尼自由振動方程

(10)

將u=Usinwt和θ=Θsinwt代入式(7)，即可得到系統的特征方程為

(11)

解得

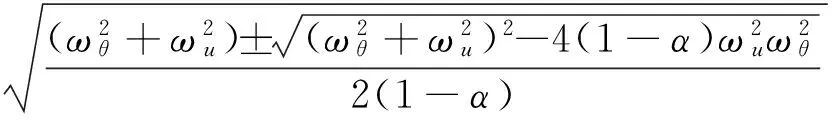
(12)

其中,

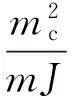
(13)

顯然，當不考慮耦合效應時，α=0，ω=ωθ=ωu，與之前得出的固有頻率是一致的。當考慮耦合效應時，固有頻率發生了變化，系統的自由振動和受迫振動均會受到影響。而且，即使只加載單一的縱向或者扭轉載荷，也會同時激發縱向和扭轉的振動。

2.2 內燃機曲軸的扭縱耦合效應

內燃機曲軸引起的扭縱耦合效應同樣不容忽略，對曲軸扭縱耦合機理的這一認識，已經得到廣泛的認可。在推進軸系的計算中，通常將曲軸扭縱耦合簡化為一個當量耦合剛度。參照文獻[13]，將柴油機曲軸的耦合效應用當量耦合剛度ki,i+1(i=1,2,…,n-1；n為柴油機集總質量數目)表示。因此，對于第j和第j+1個集總質量，其扭縱耦合效應可以由以下耦合剛度矩陣表示

(14)

顯然，式(14)中的矩陣元素和式(6)～式(7)中矩陣的非對角元素，都將軸系的扭轉和縱向振動耦合在一起。因此，將曲軸耦合剛度矩陣、附水質量矩陣和附水阻尼矩陣加入式(4)中，即可得到系統的扭縱耦合運動方程

(15)

式中，Mc、Cc和Kc分別為扭縱耦合系統的質量矩陣、阻尼矩陣和剛度矩陣。

3 數值仿真

本文以文獻[16]中的6S50MC-C型柴油機軸系為研究對象，該軸系結構示意圖如圖3所示。該型號柴油機為6缸2沖程，最大持續功率為9 480 kW，額定轉速為127 r/min，單缸振動質量為2 721 kg；螺旋槳葉片數為4，直徑6 000 mm，平均螺距3 909 mm，槳葉展開面積比0.553，螺旋槳重25 217 kg(空氣中)。其余參數詳見文獻[16]。

圖3 推進軸系模型

3.1 自由振動

該軸系劃分為24個節點，11個圓盤元件，1個推力軸承，23個軸段。各氣缸間的曲軸按照文獻[16]給出的剛度簡化為具有同等剛度的軸段。在此，我們定義三種系統并進行比較，以便得出后續結論。①無耦合無附水系統：將各元件的質量矩陣和剛度矩陣組裝成總體剛度和質量矩陣，選取扭轉和縱向的內外阻尼系數，生成總體阻尼矩陣，得到式(4)所描述的推進軸系無耦合運動方程。②無耦合系統：在式(4)中，僅加入附水質量矩陣和附水阻尼矩陣的對角元素，即不加入耦合項，將這種運動方程對應的系統定義為無耦合系統。③耦合系統：將曲軸耦合剛度矩陣、附水質量矩陣和附水阻尼矩陣都加入運動方程，即得到式(9)所描述的推進軸系的耦合運動方程，將相應的系統定義為耦合系統。表1列出了無耦合無附水系統、無耦合系統、耦合系統的固有頻率，并與文獻[16](未考慮附水效應)的計算結果進行了對比。

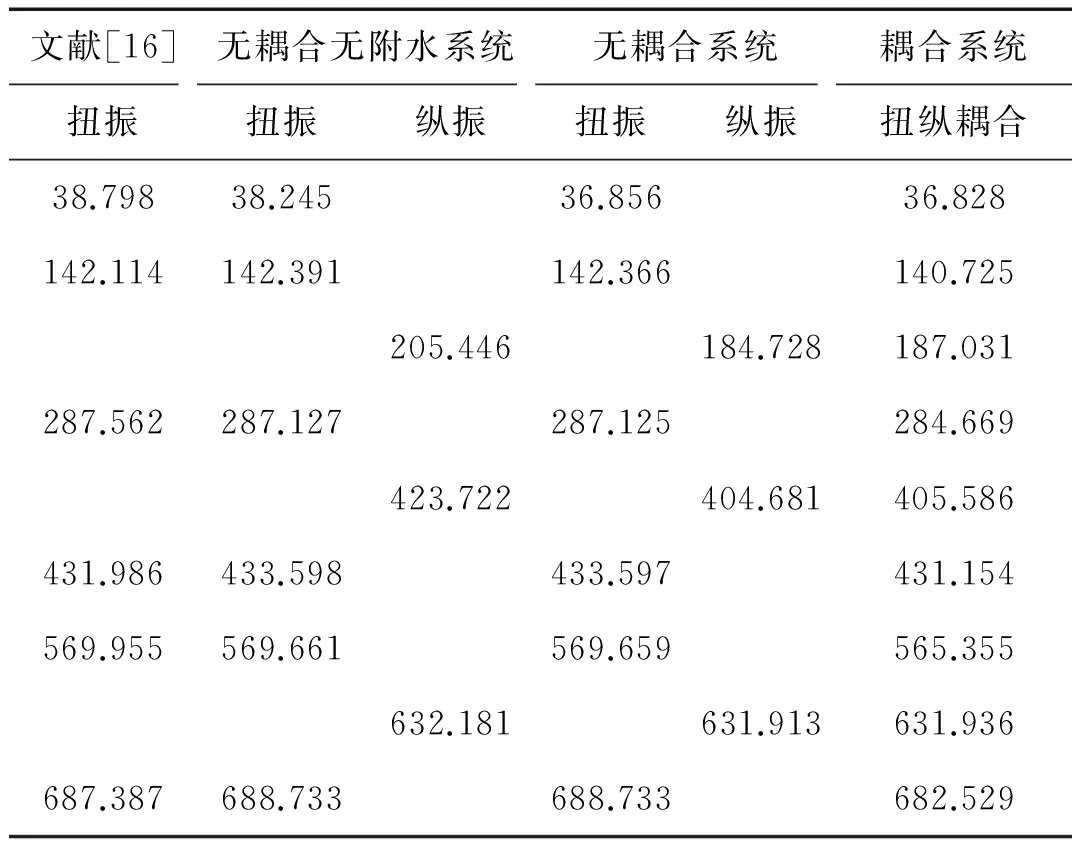
表1 三種系統的固有頻率

由于文獻[16]僅研究了軸系扭振特性，因此僅給出了扭振的固有頻率。比較文獻[16]與無耦合無附水系統的固有頻率，可以發現二者結果基本一致，誤差很小，因此本文所建立的有限元模型是可靠的。比較無耦合無附水系統與無耦合系統的固有頻率，可以發現附水慣性與阻尼對扭振頻率的影響不是十分顯著，而對縱振頻率的影響較大。這是由于按照文獻[15]的計算，該螺旋槳附水質量相對于螺旋槳自身重量較大，而附水轉動慣量相對于螺旋槳自身轉動慣量較小。因此附水質量對系統的影響更為明顯，導致了縱振的固有頻率變化較大。比較無耦合系統與耦合系統的固有頻率，可以發現扭縱耦合效應對系統的固有頻率影響并不明顯，這與文獻[15]得出的結論是一致的。

3.2 沖擊響應

本文旨在研究耦合效應對推進軸系沖擊特性的影響，因此接下來只給出無耦合系統和耦合系統的沖擊響應。

3.2.1 沖擊輸入激勵

參照德國海軍規范BV043/85，縱向沖擊輸入激勵可根據設計沖擊譜等效為雙三角波，如圖4所示。波形參數的詳細計算公式為

a2=0.6a0V1=0.75v0

t3=2V1/a2t2=0.4t3

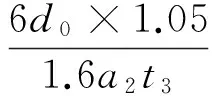
t4=t3+0.6(t5-t3)

(16)

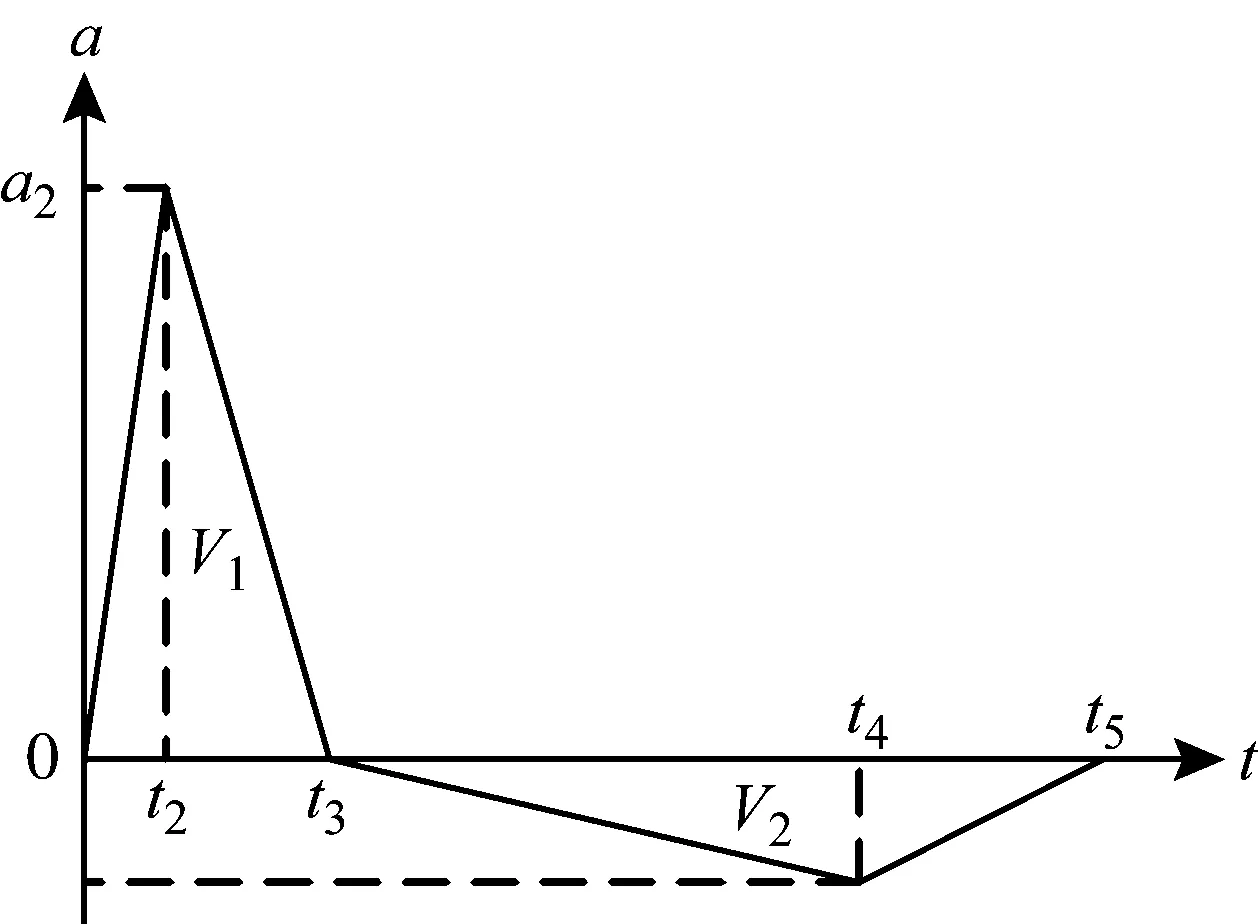
圖4 縱向沖擊輸入激勵時間歷程曲線

扭轉沖擊輸入激勵為冰載荷沖擊。螺旋槳旋轉時每個葉片依次與冰塊發生碰撞，產生的扭轉沖擊可假定為半正弦波形力矩。總的力矩即為槳葉依次作用力矩在時間軸上的疊加。計算公式參考文獻[17]，得到的扭矩如圖5所示。

圖5 扭轉沖擊輸入激勵時間歷程曲線

3.2.2 縱向沖擊

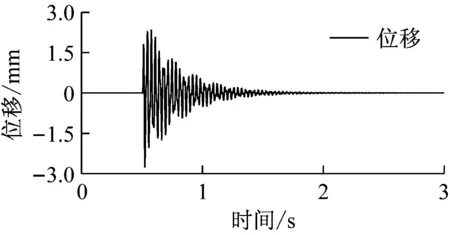
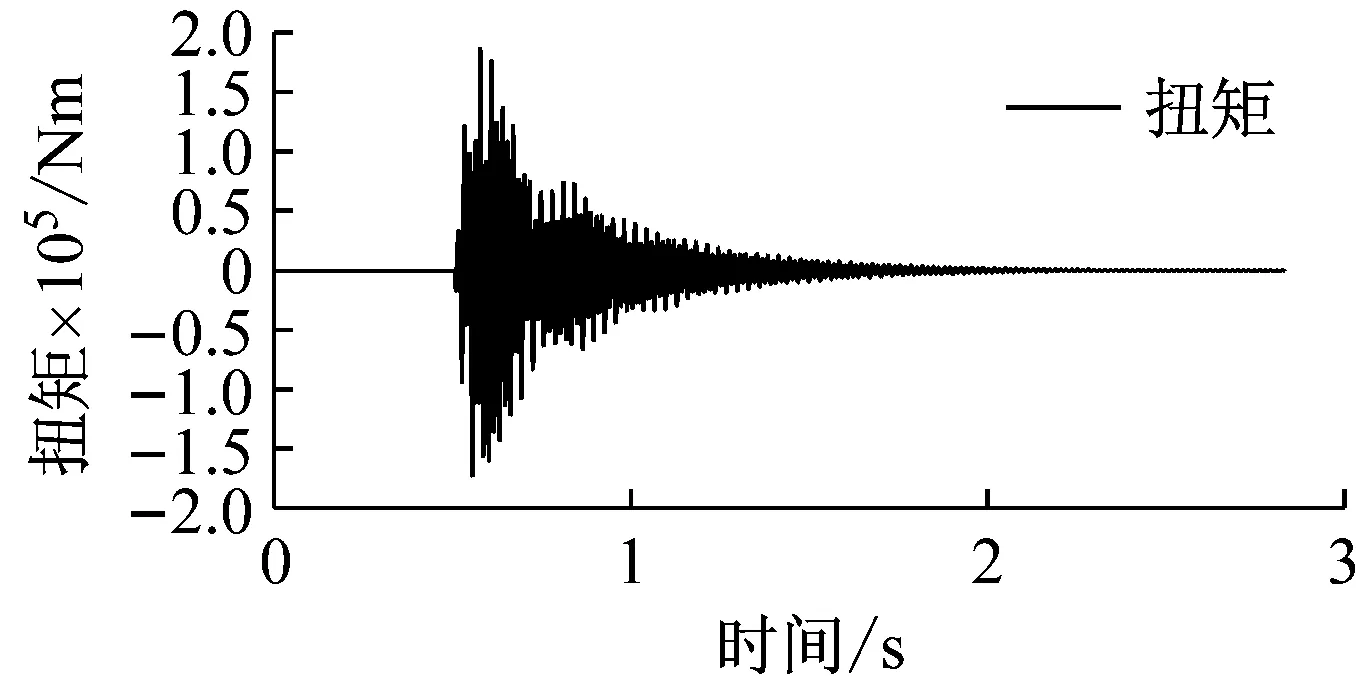
首先，僅對螺旋槳處施加縱向沖擊。當沖擊載荷為雙三角波時，無耦合系統1號節點縱向位移響應與1號軸段的扭矩如圖6所示。由圖可以看出，0.5s時沖擊載荷施加于螺旋槳處，由于縱向沖擊激勵作用時間非常短，因此位移迅速增大并很快達到最大值，之后在阻尼的作用下逐漸減小，2.0s后逐漸衰減為0。另一方面，當沒有耦合效應時，縱向沖擊只激發了縱向振動，而沒有引起扭轉振動，因此1號軸段的扭矩并未發生變化。耦合系統的響應如圖7所示。顯然，耦合效應的加入使得縱向沖擊激發了扭轉振動，1號軸段的扭矩產生了劇烈震蕩，其振動形式與縱振形式一致。同時，可以發現無耦合系統的縱振響應與耦合系統的縱振響應基本相同，說明扭縱耦合效應對縱向沖擊下的縱向振動影響很小。

(a)

(b)

圖6 縱向沖擊下無耦合系統的1號節點縱向位移與1號軸段扭矩

Fig.6Longitudinaldisplacementandtorqueofuncoupledsystemunderlongitudinalshock

(a)

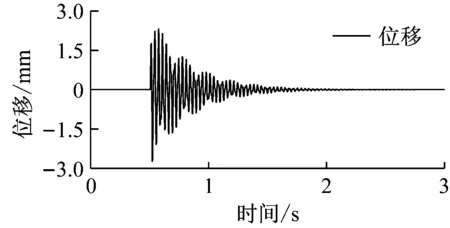
(b)

圖7 縱向沖擊下耦合系統的1號節點縱向位移與1號軸段扭矩

Fig.7Longitudinaldisplacementandtorqueofcoupledsystemunderlongitudinalshock

耦合系統各節點位移最大響應如圖8所示。隨著節點編號的增大，位移逐漸減小，到10節點也就是推力軸承處時，位移達到最小，之后逐漸增大，在螺旋槳處位移響應達到最大。縱向沖擊激發的各軸段扭矩最大響應如圖9所示，可以看出，最大值出現在第10個軸段，也就是推力軸承與飛輪之間的軸段。最小扭矩則出現在第11個軸段。

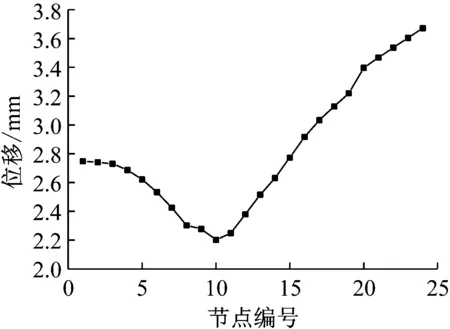
圖8 縱向沖擊下耦合系統各個節點最大位移

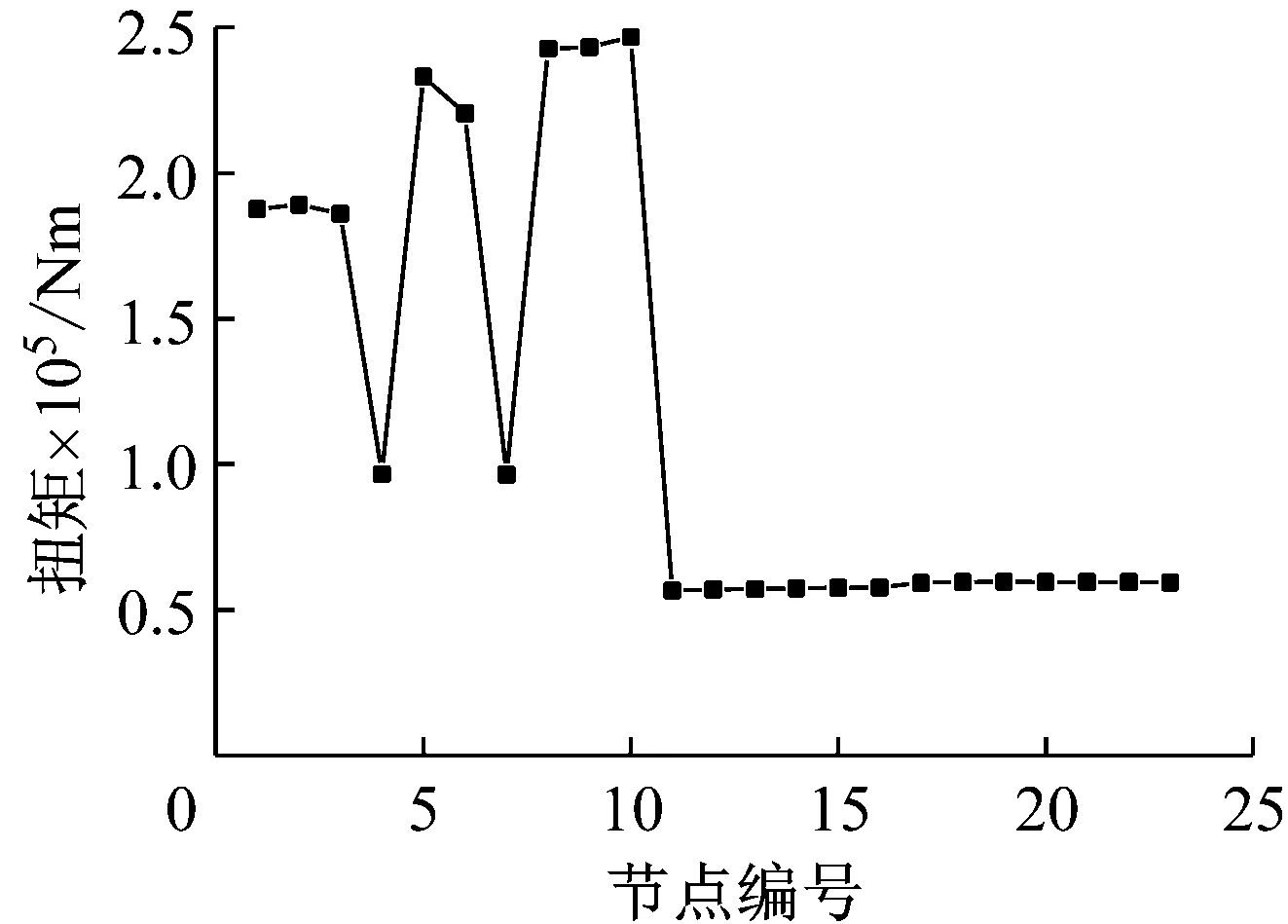
圖9 縱向沖擊下耦合系統各個軸段最大扭矩

3.2.3 扭轉沖擊

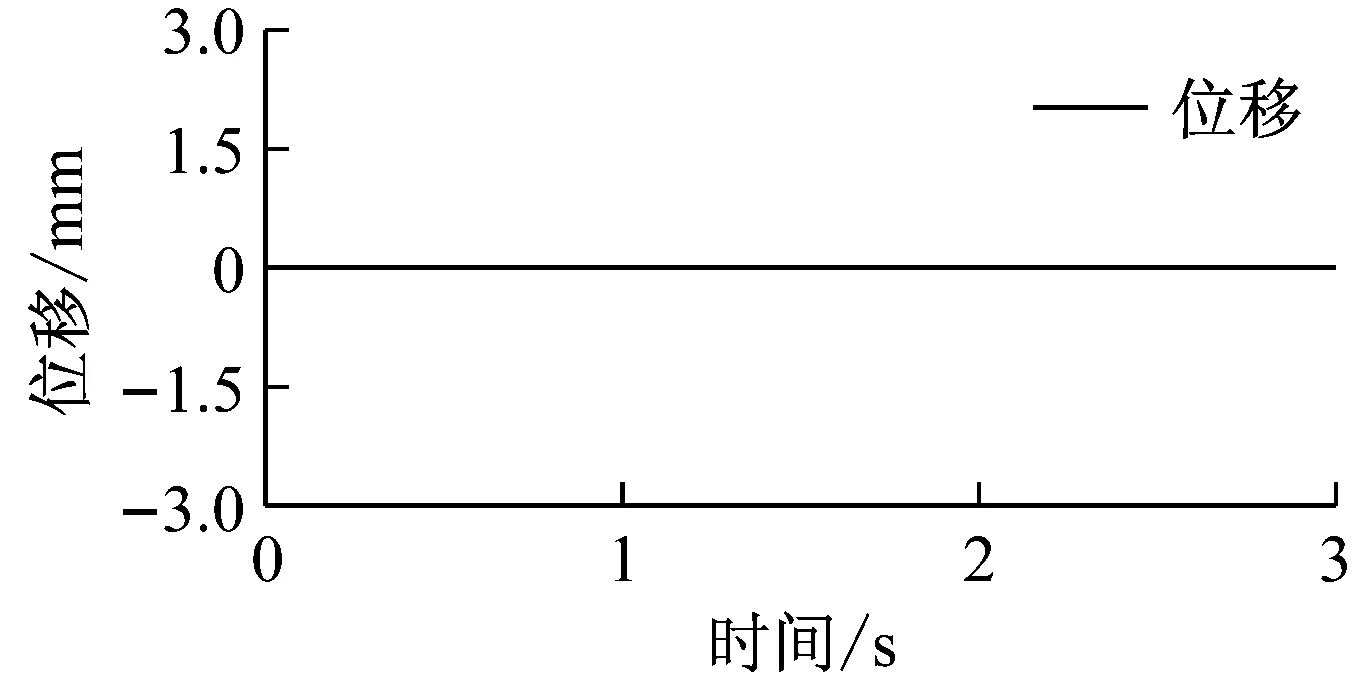
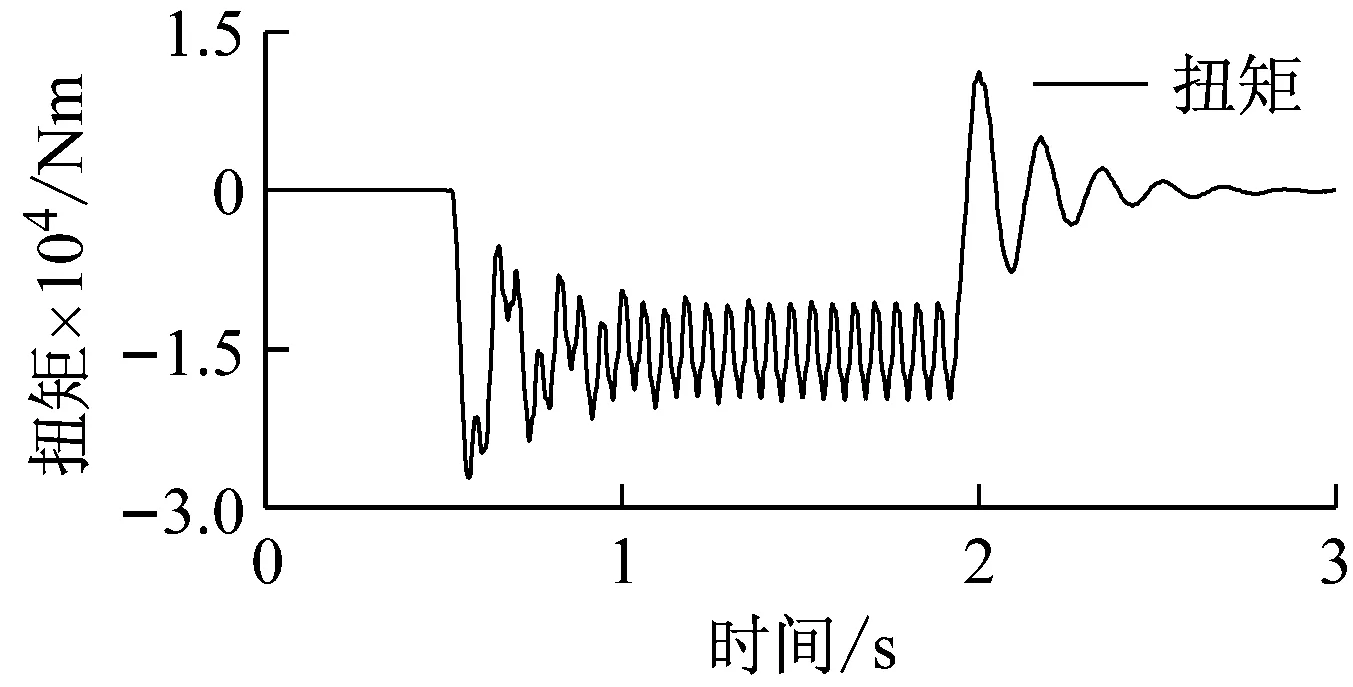
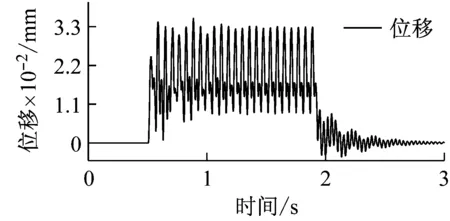
對螺旋槳施加冰載荷沖擊，無耦合系統1號節點縱向位移響應與1號軸段的扭矩如圖10所示。0.5s時冰載荷沖擊作用于螺旋槳處，扭矩迅速增大，由于冰載荷沖擊具有周期性，因此在沖擊時間內(0.5～1.92s)扭矩的波動逐漸趨于穩定。沖擊結束后，扭矩逐漸衰減至0。同樣可以看出，由于沒有加入耦合效應，扭轉沖擊并未引起縱向振動，因此1號節點的縱向位移響應為0。圖11為扭轉沖擊作用下耦合系統1號節點的縱向位移響應和1號軸段的扭矩，耦合效應使得扭轉沖擊引起了明顯的縱向振動，其振動形式與扭振形式一致。比較圖10和圖11，可以看出扭轉沖擊下無耦合系統的扭矩與耦合系統的扭矩基本相同，說明扭縱耦合效應對扭轉沖擊下的扭轉振動影響不大。

圖12給出了耦合系統各個軸段扭矩的最大響應。由于扭轉沖擊直接作用于螺旋槳，因此23號軸段扭矩最大。隨著節點編號的減小，扭矩逐漸減小。扭轉沖擊激發的各個節點位移的最大響應如圖13所示。最大位移在24號節點，也就是螺旋槳處，最小位移在10號節點，即推力軸承處。

4 結 論

本文建立了船舶推進軸系的扭縱耦合有限元模型，以某船舶推進軸系為例研究了扭縱耦合效應對軸系自由振動的影響，并進行了沖擊響應的仿真計算，得出了以下結論：

(1) 對于該推進軸系，附水效應會顯著降低縱振固有頻率，但對扭振固有頻率影響較小；而扭縱耦合效應對固有頻率影響并不明顯。

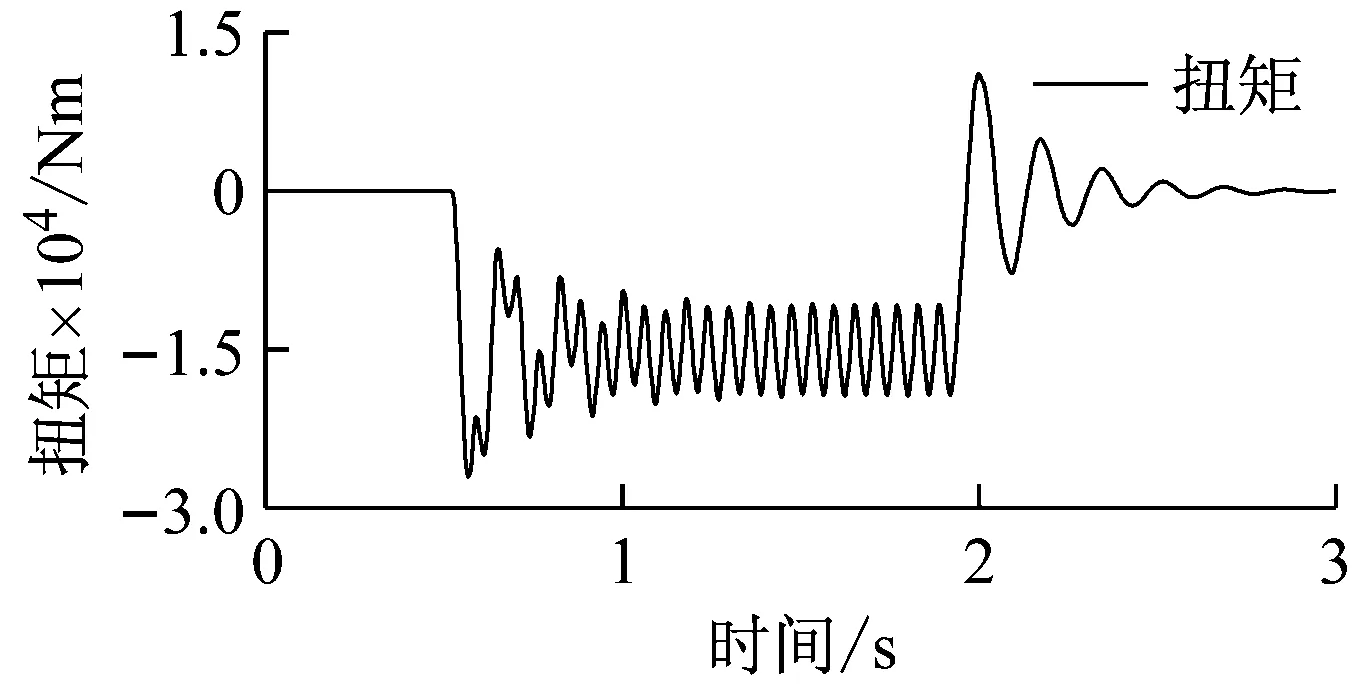
(a)

(b)

圖10 扭轉沖擊下無耦合系統的1號節點縱向位移與1號軸段扭矩

Fig.10Longitudinaldisplacementandtorqueofuncoupledsystemundertorsionalshock

(a)

(b)

圖11 扭轉沖擊下耦合系統的1號節點縱向位移與1號軸段 扭矩

Fig.11Longitudinaldisplacementandtorqueofcoupledsystemundertorsionalshock

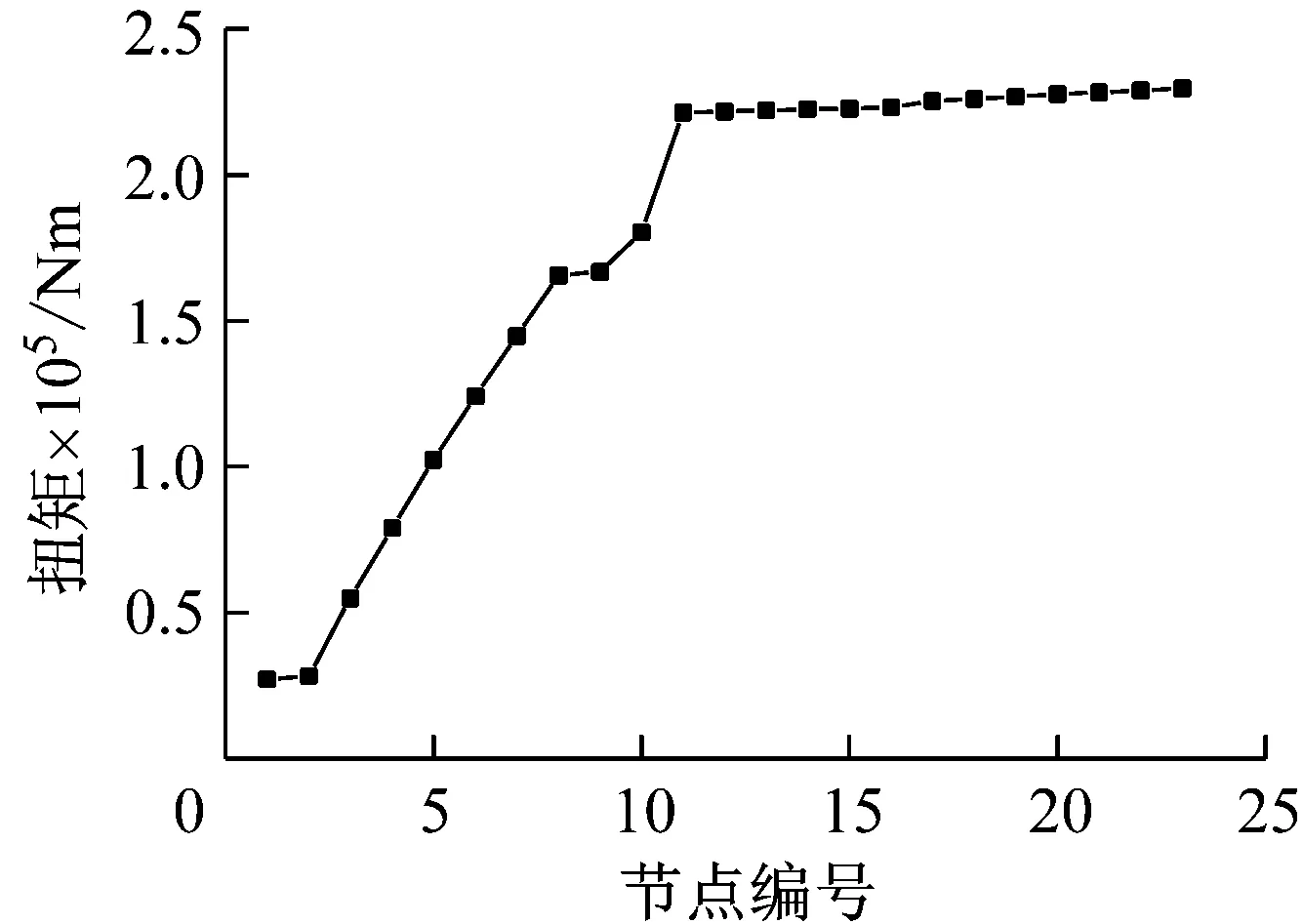
圖12 扭轉沖擊下耦合系統各個軸段最大扭矩

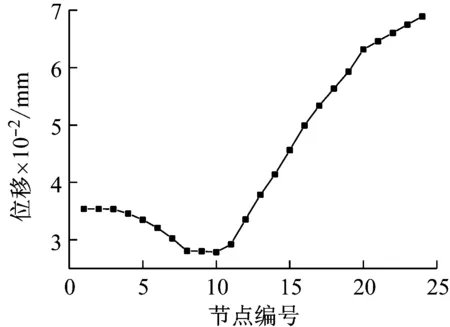
圖13 扭轉沖擊下耦合系統各個節點最大位移

(2) 扭縱耦合效應會使得縱向(扭轉)沖擊激發明顯的扭轉(縱向)振動，但基本不改變縱向(扭轉)沖擊下的縱向(扭轉)振動。

(3) 當耦合系統受到雙三角波沖擊載荷時，縱向位移會迅速增大，隨后在阻尼的作用下逐漸衰減為0，同時引起明顯的軸段扭矩振動，其振動形式與位移是一致的。當耦合系統受到冰載荷沖擊時，軸段扭矩迅速增大，之后保持周期性振動，載荷消失后，扭矩逐漸衰減為0，同樣會引起明顯的縱向位移振動，其趨勢與扭矩是一致的。

(4) 當沖擊作用于螺旋槳處時，冰載荷沖擊下，系統的最大位移響應和最大扭矩都出現在螺旋槳和靠近螺旋槳的軸段。雙三角波載荷沖擊下，系統的最大位移響應出現在螺旋槳處，但扭矩的最大值并不在靠近螺旋槳的軸段。因此，在推進軸系的沖擊設計時，應考慮在不同位置加載沖擊載荷，計算各個節點的位移與扭矩響應，來預測有可能的危險工況。

[1] 汪玉, 計晨, 杜儉業,等. 艦船動力軸系沖擊響應性能分析[J]. 振動與沖擊, 2011, 30(5):164-168.

WANGYu,JIChen,DUJianye,etal.Shockresponseanalysisofashippowershaftingsystem[J].JournalofVibrationandShock, 2011, 30(5):164-168.

[2] 于大鵬, 汪玉, 杜儉業. 不同激勵載荷下水面艦艇推進軸系沖擊響應分析[J]. 船舶工程, 2012(增刊2):46-51.

YUDapeng,WANGYu,DUJianye.Shockresponseanalysisofwarshippropulsiveshaftsubjectedtodifferentexcitation[J].ShipEngineering, 2012(Sup2):46-51.

[3] 黃冰陽, 吳煒, 陳汝剛,等. 船舶推進軸系沖擊建模和仿真研究[J]. 船海工程, 2012, 41(2):43-46.

HUANGBingyang,WUWei,CHENRugang,etal.Modelingandsimulationforimpactofthepropulsionshafting[J].Ship&OceanEngineering, 2012,41(2):43-46.

[4] 韓江桂, 吳新躍, 賀少華. 船舶推進軸系沖擊響應計算方法[J]. 艦船科學技術, 2012, 34(1):45-49.

HANJianggui,WUXinyue,HEShaohua.Researchonshockresponsemethodofshippropulsiveshafting[J].ShipScience&Technology, 2012,34(1):45-49.

[5] 孫洪軍, 鄭榮. 船舶推進軸系抗沖擊動力學建模與仿真[J]. 噪聲與振動控制, 2003, 23(4):16-18.

SUNHongjun,ZHENGRong.Modelingandsimulationofanti-shockdynamicsforpropulsiveshaftingofship[J].Noise&VibrationControl, 2003,23(4):16-18.

[6] 沈榮瀛, 張智勇, 汪玉. 船舶推進軸系沖擊響應[J]. 中國造船, 2000, 41(3):74-79.

SHENRongying,ZHANGZhiyong,WANGYu.Shockresponseofpropulsiveshaftofvessels[J].ShipbuildingofChina, 2000,41(3):74-79.

[7] 朱小平, 馮奇. 船舶主推進系統沖擊研究[J]. 船舶力學, 2007, 11(1):143-151.

ZHUXiaoping,FENGQi.Shockanalysisofthemainpropulsionshaftoftheship[J].JournalofShipMechanics, 2007,11(1):143-151.

[8] 朱小平, 馮奇. 考慮油膜力作用的船舶主推進系統沖擊研究[J]. 力學季刊, 2007, 28(4):653-660.

ZHUXiaoping,FENGQi.Shockanalysisofmainpropulsionshipshaftwithoilfilmforceconsideration[J].ChineseQuarterlyofMechanics, 2007, 28(4):653-660.

[9] 孫洪軍, 沈榮瀛, 沈密群,等. 船舶推進軸系沖擊特性試驗研究[J]. 船舶工程, 2006, 28(6):21-23.

SUNHongjun,SHENRongying,SHENMiqun,etal.Experimentalstudyonshockperformanceofmarinepropulsiveshafting[J].ShipEngineering, 2006,28(6):21-23.

[10] 朱漢華, 嚴新平, 劉正林,等. 沖擊載荷下船舶軸系轉速與回旋振動間影響研究[J]. 武漢理工大學學報(交通科學與工程版), 2008, 32(6):983-985.

ZHUHanhua,YANXinping,LIUZhenglin,etal.Researchonimpactresponserelationshipbetweentherotatingspeedandlateralvibration[J].JournalofWuhanUniversityofTechnology(TransportationScience&Engineering), 2008,32(6):983-985.

[11] 張金國, 佟軼杰, 姚世衛,等. 艦艇大功率推進軸系三向沖擊響應分析研究[J]. 艦船科學技術, 2005, 27(增刊1):24-26.

ZHANGJinguo,TONGYijie,YAOShiwei,etal.Studyingonthreeorientationsshockresponseofshiphigh-powerpropulsiveshafting[J].ShipScience&Technology, 2005, 27(Sup1):24-26.

[12] 楊紅軍, 車馳東, 張維競,等. 冰載荷沖擊下的船舶推進軸系瞬態扭轉振動響應分析[J]. 船舶力學, 2015(增刊1):176-181.

YANGHongjun,CHEChidong,ZHANGWeijing,etal.Transienttorsionalvibrationanalysisforiceimpactofshippropulsionshaft[J].JournalofShipMechanics, 2015(Sup1):176-181.

[13] 張洪田, 張志華, 劉志剛,等. 船舶推進軸系縱扭耦合振動研究[J]. 中國造船, 1995(2):68-76.

ZHANGHongtian,ZHANGZhihua,LIUZhigang,etal.Astudyoncoupledaxialandtorsionalvibrationofmarinepropulsionshafting[J].ShipbuildingofChina, 1995(2):68-76.

[14] 曾攀. 有限元分析基礎教程[M]. 北京: 清華大學, 2008.

[15]PARSONSMG.Modecouplingintorsionalandlongitudinalshaftingvibrations[J].Propellers, 1983, 20(3):257-271.

[16] 張冶. 6S50MC-C船舶柴油機軸系扭轉振動計算研究[D]. 大連:大連海事大學, 2009.

[17]POLICD,EHLERSS,AESOYV,etal.Propulsionmachineryoperatinginice-amodellingandsimulationapproach[C]∥Proceedings27thEuropeanConferenceonModellingandSimulation.Alesund: [s.n.],2013:191-197.

Torsional-longitudinal shock responses of a ship propulsion shaft system

YANG Yi, WANG Xurong, WANG Mingkun, WU Yi, DAI Yiping

(School of Energy and Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

A torsional-longitudinal shock finite element model for a diesel engine’s propulsion shaft system was established considering torsional-longitudinal coupled effects caused by the diesel engine’s crankshaft, and added hydrodynamic inertia and damping of a ship’s propeller. The free vibration and torsional-longitudinal shock responses of the coupled system were studied and compared with those of the uncoupled system to analyze influences of torsional-longitudinal coupled effects on the free vibration and shock responses of the propulsion shaft system. Results showed that the torsional-longitudinal coupled effects have little influence on the natural frequencies of the propulsion shaft system, but they obviously influence the shock responses of the propulsion shaft system; under the torsional-longitudinal coupled effects, either a single longitudinal shock or a single torsional one can simultaneously excite longitudinal vibration and torsional one to cause larger fluctuations of displacements and torques, and threaten the operation security of the shaft system, so enough attentions must be paid to torsional-longitudinal shock responses of a ship propulsion shaft system in its design stage.

ship propulsion shaft system; shock response; torsional-longitudinal coupled effect

2016-02-02 修改稿收到日期：2016-05-06

楊翼 男，博士生，1992年生

戴義平 男，博士，博士生導師，教授，1961年生

U664.21

A

10.13465/j.cnki.jvs.2017.13.015