帶漸消因子的容積卡爾曼濾波算法
賀 姍,師 昕
(西安工程大學計算機科學學院,陜西 西安 710048)
帶漸消因子的容積卡爾曼濾波算法
賀 姍,師 昕
(西安工程大學計算機科學學院,陜西 西安 710048)
在實際的非線性系統濾波問題中,會出現模型不匹配的情況,而標準容積卡爾曼濾波器對于這種模型不確定性的魯棒性比較差,其濾波估計后的效果會出現較大的偏差。針對這個問題,結合強跟蹤濾波器的思想,提出了一種新的帶漸消因子的容積卡爾曼濾波算法。這個算法的主要思想是,在濾波過程中,引入漸消因子修正濾波器的狀態協方差矩陣。應用這種方法能夠獲得比容積卡爾曼濾波更高的濾波精度。
非線性系統;強跟蹤濾波;容積卡爾曼濾波;卡爾曼濾波
在狀態估計中,如果為非線性系統,通常采用擴展卡爾曼濾波(Extended Kalman Filter,EKF)。這個算法的主要思想是,通過對系統的非線性方程進行泰勒級數展開,截取一階項或二階項對非線性函數進行線性化近似,再通過卡爾曼濾波器處理。2009年,Arasaratnam提出了容積卡爾曼濾波(Cubature Kalman Filtering,CKF),它是一種確定點采樣濾波算法。然而在實際應用過程中,可能出現系統初始狀態建模不準確的問題。
針對這個問題,周東華等人提出了強跟蹤濾波器。強跟蹤濾波器應對系統產生的狀態突變等問題,該方法的濾波精度比較高。隨后,在周東華等人提出的強跟蹤濾波算法的基礎上,又提出了一系列的改進算法,例如擴展卡爾曼濾波強跟蹤算法(Strong Tracking Extended Kalman Filter,SEKF)濾波。
該算法通過引入強跟蹤濾波因子修正濾波器的狀態預測協方差矩陣,具有較強的跟蹤性。本文將強跟蹤濾波器算法應用到了容積卡爾曼濾波器算法中,提出了帶漸消因子的容積卡爾曼濾波算法。
1 帶漸消因子的容積卡爾曼濾波
針對濾波過程中出現的模型不確定性問題,基于前人所提出的強跟蹤濾波算法,可以得到一種改進的濾波方法,即帶漸消因子的容積卡爾曼濾波算法。該算法可以有效克服模型的不確定性。一個濾波器具有強跟蹤性能的充分條件是需要滿足正交性原理。正交性原理是,一個濾波器要成為強跟蹤濾波器的充分條件是,在線選擇一個適當的時變增益矩陣,從而得出:

式(1)中:γk為量測估計值與量測真實值間的誤差(殘差)。
當出現系統模型不匹配的情況時,需要在線調整時變增益矩陣,讓殘差序列仍然保持正交性,使得濾波器仍能滿足正交性原理,能夠保持較強的跟蹤能力。為了使得濾波器具有強跟蹤濾波器的特性,可以引入一個時變的漸消因子λ。具體實現方法是,在強跟蹤容積卡爾曼濾波的預測誤差協方差陣中引入漸消因子,而量測更新部分與標準容積卡爾曼濾波算法相同,此處不再贅述。
算法1是在線求解漸消因子λ,即:

式(2)中:ρ為遺忘因子,0.95≤ρ≤0.995;lk為弱化因子,lk≥1.
第一步,初始狀態協方差因式分解:
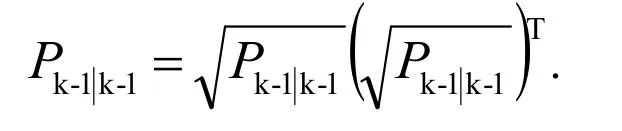
第二步,計算積分點:

第三步,計算修正之后的積分點,得到新的積分點Xl,k-1│k-1.
第四步,計算增值積分點:

第五步,計算公式(3),得到估計狀態,然后計算公式(4),得到預測誤差協方差:

2 仿真實驗和結果分析
針對單變量非穩定增長模型(Univariate Nonstationary Growth Model,UNGM),可得:

3 結論
針對非線性系統濾波問題,本文結合相關學者提出的強跟蹤濾波算法,提出了帶漸消因子的容積卡爾曼濾波算法。針對容積卡爾曼濾波對于模型不確定性的魯棒性比較差這一問題,利用強跟蹤濾波器在線調整增益矩陣,使得系統輸出的殘差序列仍然保持正交,則可以使得濾波器在實際系統中具有更強的跟蹤性能。
實驗仿真的結果表明,與標準容積卡爾曼濾波器相比,本文提出的帶漸消因子的容積卡爾曼濾波算法,能夠獲得更高的濾波精度,均方根誤差比較小。

圖1 容積卡爾曼濾波算法估計誤差

圖2 強跟蹤容積卡爾曼濾波算法估計誤差
[1]PS Maybeck,EJ Balder.Book-Review-Stochastic Models Estimation and Control.Space Science Reviews,1980,26(8):868-869.
[2]Arssaratnam I,Haykin S.Cubature Kalman filters.IEEE Trans onAutomatic Control,2009,54(6):1254-1269.
[3]周東華,席裕庚,張鐘俊.非線性系統的帶次優漸消因子的擴展卡爾曼濾波[J].控制與決策,1990,5(5):1-6.
[4]周東華,席裕庚,張鐘俊.一種帶多重次優漸消因子的擴展卡爾曼濾波器[J].自動化學報,1991,17(6):690-695.
[5]付夢印,鄧志紅,閆麗萍.Kalman濾波理論及其在導航系統中的應用[M].北京:科學出版社,2010:100-103.
[6]范文兵,劉春風,張素貞.一種強跟蹤擴展卡爾曼濾波器的改進算法[J].控制和決策,2010,21(1):74-76.本文部分參考文獻因著錄項目不全被刪除。
〔編輯:白潔〕
TN97
A
10.15913/j.cnki.kjycx.2017.13.001
2095-6835(2017)13-0001-02

