淺談極限的幾何意義在高等數學教學中的運用
劉瓊玲++王林林
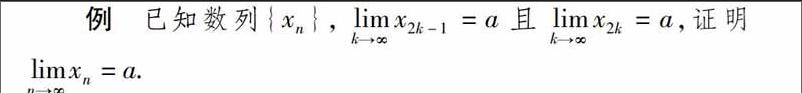

【摘要】極限是高等數學的核心內容之一,對極限定義的理解常常是高等數學教學的難點.本文從數列極限的幾何意義入手,借助幾何意義的直觀性來理解極限的定義,詳細分析了極限的有界性、唯一性、保號性等重要性質,并舉例說明了如何從幾何意義的角度尋找部分問題的解題思路.
【關鍵詞】極限;幾何意義;數列
【基金項目】國家自然科學基金(11501561);中國礦業大學基本科研業務費項目(2014QNA58).
一、引言
極限思想貫穿整個高等數學始終,是高等數學學習的基礎,高等數學中的許多概念及運算法則都是建立在極限的基礎之上,因此,在高等數學教學中,使學生充分理解極限的定義、內涵和性質等是十分必要的.而通過幾何意義體現出的生動活潑的極限思想,能夠提高學生的學習興趣,加深學生對極限本質的認識,使得這一概念不再僅僅是一種形式化的表達.
在教學過程中,首先,從幾何意義的角度給出直觀的幾何解釋,提起學生的學習興趣,使得學生對概念或性質等有個直觀的印象和初步的理解,然后,進行嚴格的理論推導,可使學生理解起來相對容易,更加容易掌握定義和性質的內涵,會收到較好的教學效果.
二、數列極限的定義和幾何意義
(一)定義(ε-N語言)[1]
對于數列{xn}及常數a,ε>0(無論多么小),總存在正整數N,當n>N時,恒有|xn-a|<ε,則稱a是{xn}的極限,或稱{xn}收斂于a,記作
(二)幾何意義
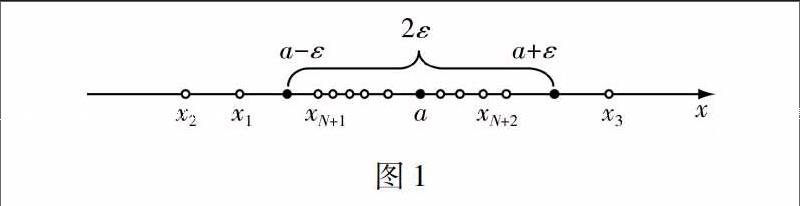
在定義中|xn-a|<εa-ε
隨著n的增大,xn代表的點越來越“密集”在點a的附近.
結合數列的幾何意義可以更加有效地向學生講解數列極限的有界性、唯一性、保號性以及數列子列的收斂性等性質.
三、從幾何意義的角度理解數列極限的性質
(一)有界性:如果數列{xn}收斂,則數列{xn}一定有界
分析設 limn→∞xn=a,根據上述幾何意義,對于任一給定的正數ε,一定都有正整數N,數列{xn}從第N+1項開始都落在區間(a-ε,a+ε)里面,不妨取ε=1,那么{xn}從某一項開始都落在區間(a-1,a+1)里面,剩下的有限項自然是有界的,取一個既包含區間(a-1,a+1)又包含剩下的有限多項的閉區間[-M,M]即可證明結論成立.
(二)唯一性:如果數列{xn}收斂,則極限唯一
(四)數列子列的收斂性:如果數列{xn}收斂于a,則它的任一子列{xnk}都收斂于a
分析設 limn→∞xn=a,根據極限的幾何意義,對于任一給定的正數ε,都存在正整數N,數列{xn}從第N+1項開始都落在區間(a-ε,a+ε)里面,在區間(a-ε,a+ε)外面只有數列{xn}中的有限項,而{xnk}作為{xn}的子列,自然也只有有限項落在區間(a-ε,a+ε)外面,于是可以找到正整數N*,使得{xnk}從第N*+1項開始都落在區間(a-ε,a+ε)里面,這就說明{xnk}同樣收斂于a.
對于函數f(x)的極限,可以類似地討論其幾何意義并從幾何意義的角度分析其性質,這里就不再累述.
四、運用幾何意義分析問題并尋找證題思路
部分關于極限的證明題,同樣可以從幾何意義的角度來理解,從而找到解決問題的正確思路.
分析因為 limk→∞x2k-1=a且 limk→∞x2k=a,根據幾何意義可知,對于任一給定的正數ε,可以找到共同的正整數N,數列{x2k-1}和{x2k}均從第N+1項開始都落在區間(a-ε,a+ε)里面,在區間(a-ε,a+ε)外面只有{x2k-1}和{x2k}中的有限項,因此,在區間(a-ε,a+ε)外面必然只有數列{xn}中的有限項,這就說明了{xn}也是收斂于a.
在高等數學中,類似的問題還有很多,例如,導數[3]、微分中值定理、定積分等等,均有其幾何意義,從幾何直觀出發對相應的問題進行分析可以加深對概念或問題內涵的理解,使得抽象復雜的數學問題變得形象直觀,在教學中合理運用這些幾何意義,不僅能夠使得教師的教學活動事半功倍,更能提高學生分析問題和解決問題的能力.
【參考文獻】
[1]同濟大學數學系.高等數學:上冊[M].北京:高等教育出版社,2007.
[2]張興永,楊宏晨,吳宗翔,逄世友,趙遷貴.高等數學:上冊[M].北京:煤炭工業出版社,2014.
[3]王芳,汪曉勤.HPM視角下“導數幾何意義”的教學[J].數學教育學報,2012,21(05):57-60.

