“等差數列前n項和”教學實錄與反思

林愛華

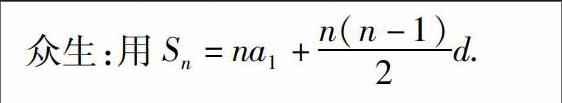
【摘要】本節課是必修5第二章第三節“等差數列的前n項和”的第一課時，主要內容是等差數列的前n項和公式的推導和簡單應用.通過本課的部分教學實錄談談對教學的幾點反思.

【關鍵詞】等差數列；前n項和；教學實錄；反思

一、創設問題情境

問題1：1+2+3+4+…+100=？

師：大家都聽說過高斯的故事吧，據說在200多年前，高斯上小學時，有一次數學老師給同學們提出了這樣的一道問題：計算1+2+3+4+…+100=？當時高斯的同學一看到題目就馬上埋頭計算起來，而唯獨他沒有這么做，他先思考，結果當他的同學都在緊張計算卻還沒有得出答案的時候，他已經舉手說：“老師，我做完了.”老師大吃一驚，原來是班上年紀最小的高斯.老師走到他身邊只見他在筆記上寫著5 050，不由得暗自稱贊.同學們，你們知道小高斯當時用了什么妙法迅速解決了這個求和問題嗎？

生1：他不是從左往右一個一個計算的.

生2：高斯發現1+100=101，2+99=101，3+98=101，…，50+51=101.因此，把1+2+3+4+…+100分成50組，每組和為101，共5 050.

師：回答得非常好！

1+2+3+4+…+100

=（1+100）+（2+99）+（3+98）+…+（50+51）

=101×50

=5050.

問題2：建筑工地上一堆圓木，從上到下每層的數目分別為1，2，3，…，9.共有多少根圓木？請用簡便的方法計算.（數據小而少，學生很快就求得結果45）

問題3：求1到n的正整數之和，即1+2+3+…+n=？

（學生們紛紛模仿小高斯的做法來算，但很快就有學生算不下去了）

生3：老師，n是奇數還是偶數？

師：都有可能.（很快有學生說出了自己的想法）

師：很好，懂得對n分類討論，要是不分類還有別的求和辦法嗎？

生5：把1+2+3+…+n各項順序倒過來，即n+（n-1）+…+3+2+1，把兩式相加再除以2即可.

師：回答得非常棒！剛才這名同學利用的是1+n=2+（n-1）=3+（n-2）=…=n+1這一特點求和.

二、課題引入

師：我們把a1+a2+a3+…+an叫作數列{an}的前n項和，記作Sn，如何求等差數列{an}前n項和Sn呢？

三、探究新知

師：設等差數列{an}的前n項和為Sn，則Sn=a1+a2+a3+…+an，能否用問題3的解決方法求和呢？請討論并推導.（筆者下去巡查了一下，發現有的組討論很激烈）

師：請一名同學說說你們組的討論結果，是如何得到的？

師：不錯，以上兩個公式都是等差數列的前n項和公式，前者反映了等差數列的任意的第k項與倒數第k項的和等于首末項的和這個性質；后者反映了等差數列的前n項和與它的首項、公差之間的關系，并且是關于n的“二次函數”.華羅庚曾說過：“數少形不直觀，形少數難入微.”你們能否認真觀察公式（1）（2）并給予幾何解釋.（學生沉默了近1分鐘，還是沒有發現哪個圖形與它們有聯系）

練習熱身：求下列等差數列{an}的前項和Sn（略）.

（這組練習目的是幫助學生熟悉公式，并能恰當地選擇合適的公式）

四、應用舉例

例1（教材第43頁例1）（讓學生閱讀并審題）

師：根據題意求這10年資金的總投入即把這10年的資金相加，而每年投入的資金是多少？

眾生：2001年是500萬元，以后每年的投入資金比上一年增加50萬元.

師：這是怎樣的一個求和問題？

眾生：等差數列，求以500為首項，以50為公差的等差數列的前10項和.

師：很好.要用哪個求和公式？

（分析完畢，利用幻燈片給出解題過程）

例2（教材第43頁例2）（讓學生閱讀并審題）

師：要確定等差數列的前n項和的公式，最基本的量有哪些？（學生回顧等差數列的前n項和的公式，明確a1與d是等差數列的兩個基本量，利用方程組思想解決）

五、練習鞏固（略）

六、教后反思

（一）對教學過程設計的反思

本節開頭以大家熟知的小高斯的故事設置情境，既激發學生的學習興趣，同時也激勵學生認真學習，淺顯的引入讓學生情緒高漲.這時又拋出第二個工地上木頭的堆放問題，層層鋪墊，引導學生從特殊到一般歸納等差數列的前n項和的推導方法，并得出結論Sn=n（a1+an）2，由an=a1+（n-1）d，進一步得到Sn=na1+n（n-1）2d.并且利用梯形面積幫助學生記憶等差數列的前n項和的兩個公式.在推導出等差數列的前n項和之后就是應用舉例，由于剛剛認識等差數列的前n項和公式，本人認為如果直接講解教材中的例1，難度較大，于是補充了三道練習，根據所給的條件求等差數列的前n項和.目的是讓學生熟悉公式，并能恰當地選擇合適的公式.最后講解教材中的例題1、2.這樣的安排符合了學生的認識規律，由易到難，層層遞進，在練習鞏固部分，通過變式，讓學生體會“思則變，變則通”的理念，同時體驗到方程組思想在解題中的運用，加深理解等差數列的前n項和公式中五個變量a1，an，n，d，Sn，只要知道其中三個就可求另外兩個，即“知三求二”.

（二）對學生評價的反思

在整個教學過程中，本人很重視學生的質疑與回答.如果對了，本人及時給予肯定，這樣可以鼓勵他們繼續積極思考并回答問題.值得一提的是在教學過程中本來并沒有預設學生對問題3的解決會采用分類的方法進行分組求和，當學生提出疑問n是奇數還是偶數時，筆者沒有直接否定他的做法而是耐心引導，及時肯定，給他留出足夠的計算時間，使他能夠順利完成1+2+3+…+n求和，并發現不論n為奇數還是偶數，和都為n（n+1）2.當筆者及時肯定他的發現時，他表現出少有的興奮，目光更有神了，聽課更專注了.雖然上課的時間較有限，但如果當時筆者假裝沒聽見不予理睬的話，那可能將會是另外一種情形，學生會感到被教師所冷落，對他的回答不關心，從而會影響他學習數學的積極性.總之，在課堂中對學生的評價要及時，多用賞識的眼光看待他們.

（三）對教學中不足的反思

由于對等差數列的前n項的公式的推導花費的時間稍多了一些，而導致最后的變式訓練和小結有些倉促.如果重新設計教學的話，筆者會適當減少練習.