用函數的觀點求解數列問題

楊梅++甯懿楠

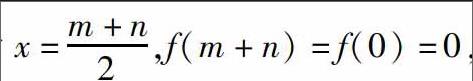
【摘要】教材將數列安排在函數之后學習，強調了數列與函數知識的密切關系，數列可看作一個定義域為N的函數，數列的通項公式就是相應的函數解析式；其圖像表示的是一群孤立的點，因此，用函數的觀點去考查數列問題也是一種有效的途徑，本文將用函數的觀點來解決數列的相關問題.

【關鍵詞】函數；等差數列；二次函數

一、利用等差數列通項公式是一次函數形式的性質

對于公差不為零的等差數列來說，它的通項是關于n的一次函數，其公差就是這個一次函數（直線）的斜率，因此，可用此思想來求得數列的公差，進而求得數列中其他的量.

例1在等差數列{an}中，a5=-3，a15=27，求數列的通項公式.

分析本題中已知數列中的兩項，求數列的通項公式，屬于基礎題，要求出數列通項的公式，應先求出公差d，再按公式寫出通項.

解題思路聯系等差數列的通項公式是關于n一次函數，且公差就是這個一次函數的斜率，題中已知的兩項可看成兩點（5，-3），（15，27），求出過這兩點直線的斜率即為該數列的公差，則可求得數列的通項公式.

二、利用Sn是n的二次函數的性質

分析該題的題干較短，可提取的信息不多，對于我們解決問題有一定的困難，若直接用公式然后令它們相等來解決問題較難，不易突破.因此，可以聯系公差不為零的等差數列的前n項和是關于項數n的二次函數，將數列問題用函數的思想求解.

解題思路（1）略.

（2）該題若從數列的角度解決有一定的困難，為了更方便地解決此題，我們可以從函數的角度思考利用公差不為零的等差數列前n項和與二次函數之間的關系可知對稱軸為 ，即Sm+n的值為零.

反思上題第二問的解答方式利用了二次函數圖像關于對稱軸對稱的性質，結合函數圖像性質分析解決數列問題能使問題轉變得更簡單.

三、利用函數的性質解數列問題

數列是特殊的函數，函數基本性質包括：單調性、周期性、奇偶性、最值性，其中函數的單調性、周期性在數列中有廣泛的應用.

（一）函數單調性在數列中的應用

解題思路由所求問題可知，首先應先求出an的形式，根據題中所給出的遞推關系很容易判斷出用累加法求通項，令f（n）=ann將所求問題轉化為函數問題，再按求函數最值的方法求最值即可，但應注意此特殊函數定義域.

反思數列是一種離散型的函數，它的單調性與函數的單調性既有聯系又有區別.在利用函數單調性解決數列的最值問題時要善于利用函數的圖像和性質來分析數列問題，同時應注意數列的定義域.

（二）函數的周期性在數列中的應用

分析此題所要求解的是該數列的第2 008項，從題中給出的已知條件我們不能套用公式，因此，我們應從周期性的角度考慮，結合函數周期的確定方法來解決此問題.

解題思路題中給出的遞推關系是連續三項之間的關系，我們可以令f（n）=an，聯系題中已知的遞推關系可以求出該函數的周期，用2 008除以周期再結合余數即可求出第2 008項的值.

反思本題主要考查數列的基本知識，關鍵在于發現所隱含的函數關系，利用周期性，從而達到解題的目的.

綜上可見，在解決較難數列問題時，常常找不到解題的突破口，使思維受阻.我們知道數列是一類特殊的函數，若能將數列問題轉化為函數問題來研究就很方便快捷.因此，當我們在解決數列問題時，要樹立函數思想及觀點，應充分利用函數的有關知識，以它的概念、性質以及圖像為紐帶，架起函數與數列之間的橋梁，揭示它們內在的聯系和區別，從而更好地解決數列問題.

【參考文獻】

[1]閆沛蓮.函數觀點下的數列問題[J].數學教學研究，2006（2）：24-26.

[2]周道平.用函數的知識解決數列問題[J].數理化學習：高三版，2013（12）：63.