基于多元統計分析的出租車資源配置模型研究
孫麗男++張璇++張靜++劉德華


【摘要】利用打車軟件智能出行平臺獲取相關數據,采用統計學方法分析不同時空出租車資源的“供需匹配”程度,為城市的出租車資源配置提供決策依據.首先,選取國內具有代表性的20個城市,利用聚類分析將其分為三類;其次,利用MATLAB對“出租車分布”和“出租車需求量分布”進行了可視化,直觀分析了三類城市出租車資源“供需匹配”程度;最后,選取適當指標,利用SPSS對數據進行主成分分析及多元線性回歸,建立了模型,量化了出租車資源“供需匹配”程度與相關指標的關系,從而可以通過控制各個指標來優化出租車資源配置.
【關鍵詞】供需匹配程度;主成分分析;聚類分析;多元線性回歸
【基金項目】2014年12月黑龍江省教育科學規劃辦重點課題,基于大數據技術的應用型本科院校統計學專業人才培養模式研究與實踐(編號:GJB1214026).
隨著人們生活水平的日益提高,城市交通網越來越發達,城市交通工具趨于多樣性,私家車擁有量逐年飆升,盡管如此,受各種政策和客觀條件的影響,出租車仍然是我國城鎮市民出行重要的交通工具.由于出租車市場監管不夠嚴格,城鄉接合部面積擴張迅速等原因,一些城市出現了“打車難”現象,特別是流動人口多的旅游城市這種現象更加突出[1].為了緩解這一現象,打車軟件應運而生并推出了許多優惠和補貼政策,一時間受到了廣大司機和消費者的青睞.與此同時,打車軟件智能出行平臺內承載的海量數據也隨著大數據時代的到來日漸凸顯其重要的價值[2],通過對這些數據進行挖掘和分析必將對有效監管出租車市場的發展、合理配置出租車資源提供決策支持.針對我們要解決的實際問題,我們需要做以下模型假設:(1)假設打車軟件系統無漏洞;(2)假設每個出租車公司出行政策相同;(3)假設每個地區軟件平均使用率相同;(4)假設每個出租車行駛里程單價相同;(5)假設出租需求與供給不受天氣影響;(6)假設道路交通里程數不變;(7)假設各個城市人口總數不變,出租車數量總數不變;
一、城市聚類分析
本小節選取聚類分析方法中系統聚類法[3]將一些重要城市聚類,為接下來的模型建立奠定基礎.我們選取人口數、出租車擁有量等指標,利用系統聚類的分類方法將上海、北京、廣州等20個主要城市進行聚類,將其分為三類,即一線交通發展城市、二線交通發展城市和三線交通發展城市.根據收集的統計數據,利用上述聚類方法,我們得到20個城市聚類后的樹狀圖,從而我們可以得到聚類分析結果,見圖1.
進一步,根據樹狀圖和指標分布情況采用最長距離法進行分類.其中,最長距離法所使用的公式為
它等于Gp與Gq中最遠的兩個樣品的距離.
根據最長距離法的定義及其公式,經過三次分類,最終將北京、廣州聚為一類,定義為一線交通發展城市;沈陽、武漢、哈爾濱、濟南、寧波、杭州、廈門和深圳聚為一類,定義為二線交通發展城市;剩余城市聚為一類,定義為相對發展較弱的三線交通發展城市.進行分類后,我們即可選取北京、沈陽和南京分別作為各類城市中的代表.
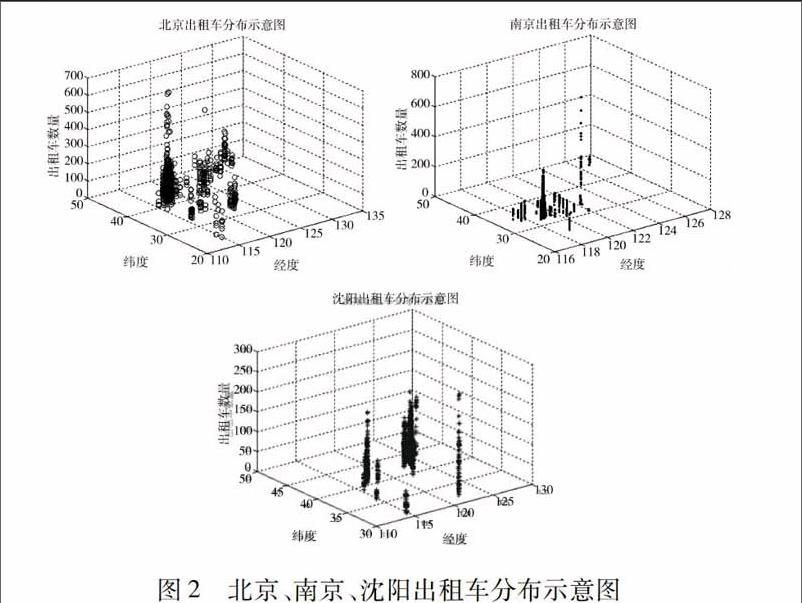
我們對北京、沈陽和南京三個城市的打車需求量與出租車分布利用MATLAB進行三維模擬,并進行兩個指標間的比較.
由圖2、圖3可知,北京出租車分布情況的密集程度與需求量的分布程度部分地區基本一致,但總體差異性比較大,即北京的供求匹配不合理,需要重新合理分配出租車分布.南京出租車分布情況的密集程度與需求量的分布程度類似,但需求量很少,由此造成出租車空載率増大,資源浪費,因此,需要重新分配出租車分布以達到供需匹配平衡.沈陽分布出現的問題與南京相同,因此,需要調整出租車分布.
二、主成分分析[4]和多元線性回歸模型
(一)模型建立
下面,我們將各城市出租車分布設為因變量y,難易度x1、需求量x2、搶單時間x3設為自變量,利用主成分分析對上述變量建立多元回歸模型,具體步驟如下:
第一步,針對三個自變量做因子分析,計算出各指標的方差累積貢獻率,得出x2與x3的累積貢獻率大于85%,貢獻率較高,x1的貢獻率不高;
第二步,根據上述分析結果選取需求量x2、搶單時間x3作為因子,利用SPSS求得主成分prin1、prin2,見表2.
第三步,用y對兩個主成分prin1和prin2做普通最小二乘,獲得主成分系數,得到主成分回歸方程為
(二)模型檢驗與分析
根據系數表,我們可知各個參數對應顯著性檢驗的p值均小于顯著性水平0.05,因此,上述模型通過檢驗.根據上述模型可知乘客對出租車的需求量與出租車的分布情況呈負相關,因此,出租車的分布與出租車的需求之間矛盾,造成出租車空載率增大,分布不合理,應有效改善出租車分布情況,提高利用率,盡可能地平衡分布與需求的關系.
(三)模型應用
下面我們通過對模型簡單應用,進一步比較觀測值和預測值,從而更直觀地感受模型的回歸效果及應用價值.
北京的模型應用:當難易度為9 452、需求量為707 154、搶單時間為604 100.55時,代入y=0.284x1-0.055x2+0479x3+56.181,得出租車分布為692 302,該數值與觀測值相差不大,本模型預測效果較佳.
沈陽的模型應用:當難易度為2 857、需求量為294 228、搶單時間為20 594.38時,代入y=0.536x1-1.559x2+0049x3+41.806,得出租車分布為291 371,該數值與觀測值相差不大,本模型預測效果較佳.
南京的模型應用:當難易度為4676、需求量為572 990、搶單時間為31 140.13時,代入y=-2.036x1-0.103x2+046x3+84.46,得出租車分布為568 314,該數值與觀測值相差不大,本模型預測效果較佳.
除了上述模型的預測應用外,其還可以進行控制應用,即政府部門或相關企業要想控制某區域內的出租車分布,可以出臺相應政策和措施調控難易度x1、需求量x2、搶單時間x3,進而達到調控出租車配置的目的.
【參考文獻】
[1]潘玉奇,周勁,楊秀麗,袁寧.基于模糊聚類分析的數據檢索的應用[J].微電子學與計算機,2005(06):167-169,172.
[2]林玉川.移動打車軟件用戶行為研究[D].廈門:廈門大學,2014.
[3]何曉群.多元統計分析[M].北京:人民大學出版社,2015.
[4]韓冰.主成分分析和神經網絡在工業經濟數據中的應用[D].長春:吉林大學,2014.

