基于VMD-SE和DE-ELM的直升機滾動軸承故障診斷方法
姚瑞琦,熊邦書,李新民,莫燕,陳新云
(1.南昌航空大學 無損檢測技術教育部重點實驗室,南昌 330063;2.中國直升機設計研究所 直升機旋翼動力學國防科技重點實驗室,江西 景德鎮 333001;3.中航通飛研究院有限公司,廣東 珠海 519040)
自動傾斜器是直升機操縱系統和旋翼系統的重要組成部分,滾動軸承作為其關鍵部件,一旦出現故障,必將影響直升機的正常飛行,因此滾動軸承的故障診斷對直升機的安全飛行具有重要意義。
軸承振動信號具有非平穩、非線性的特點,時頻域方法是基于振動信號特征提取的主流方法。經驗模態分解(Empirical Mode Decomposition,EMD)[1]作為一種自適應信號分解方法,能夠處理復雜的非線性、非平穩信號,凸顯信號的局部特征,但存在模態混疊、端點效應、過包絡和欠包絡等問題。局部均值分解(Local Mean Decomposition,LMD)[2-3]處理信號的能力全面優于EMD,但LMD屬于遞歸模式分解,仍存在一定的模態混疊和端點效應,主要表現在很難將2個頻率相近的純諧波進行分離[4]。變分模態分解(Variational Mode Decomposition,VMD)[5]采用一種非遞歸的處理策略,通過在變分框架內求解約束變分模型實現信號的分解過程[6],從而將頻率相近的2個純諧波信號分離開[7],但很難確定模態數,目前常采用中心頻率法[4]確定模態數。
極限學習機(Extreme Learning Machine,ELM)作為一種單隱層前饋神經網絡,無需調整網絡參數,只需設定神經元個數,隨機初始化輸入權重和隱含層偏置就能得到輸出權重。相對于支持向量機(Support Vector Machine,SVM),ELM的分類優勢在于人工干預更少、運行時間更快[8],已經在發動機故障診斷、電能質量分析領域獲得應用[9-10]。但ELM隨機初始化過程中容易對分類結果造成影響,因此,利用差分進化算法(Differential Evolution,DE)改進ELM,嘗試在小樣本情況下提高軸承故障識別率。
1 基于VMD-SE的特征提取
1.1 信號的變分模態分解
VMD的目標是將振動信號分解為若干圍繞在中心頻率ωk周圍的帶限模態,每個模態yk帶寬估計的主要步驟如下[5]:
1)通過Hilbert變換將模態yk轉換為解析信號,獲得一個單邊頻譜;
2)通過混合指數項調整各自估計的中心頻率,將yk的頻譜變換到基帶上;
3)通過解調信號的Η1Guess平滑對模態的帶寬進行估計。
基于以上求解過程提出一種變分約束問題,即
(1)
為解決變分約束問題,首先引入Lagrange乘子和二次懲罰因子α到增廣Lagrange表達式
(2)
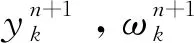
(3)
最后將(3)式轉變到頻域,得到各模態的頻域更新,即
(4)
1.2 基于SE的特征提取
VMD將各模態在頻域更新,最后又通過Fourier逆變換到時域,各模態特征提取步驟如下:
1)設其中一個模態為{x(n)},n=1,2,…,N,N為時間序列長度,將其劃分成m維向量
X(i)={X(i),X(i+1),…,X(i+m-1)};
i=1,2,…,N-m+1。
(5)
2)定義X(i)與X(j)之間的距離為
d(i,j)=max|x(i+k)-x(j+k)|;k=0,1,…,m-1。
(6)
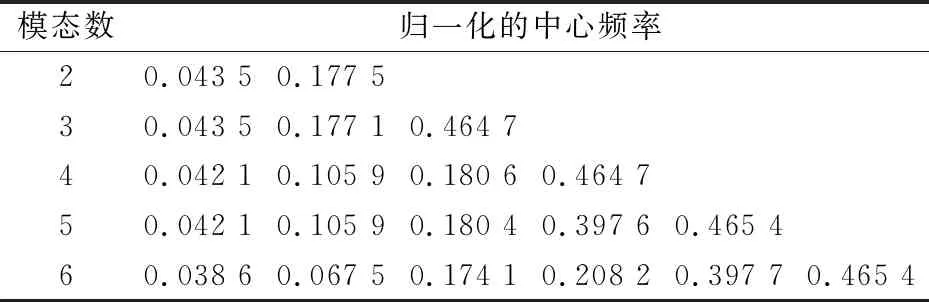
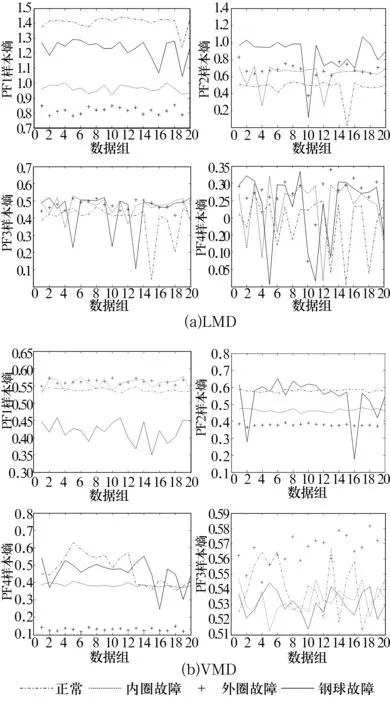
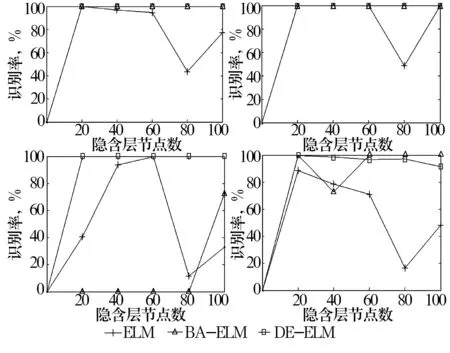
給定閾值r,統計d(i,j) (7) (8) 4)將維數加1,重復上述步驟可得Bm+1(r)。 5)樣本熵(Sample Entropy,SE)的定義為 SSE(m,r,N)=-ln[Bm+1(r)/Bm(r)]。 (9) 差分進化算法是一種新的基于種群迭代的群體智能優化算法,具有原理簡單、受控參數少、魯棒性強的特點,目前在優化計算領域已廣泛應用。DE的基本流程為[11]: 2.1.1 初始化 設D為個體維數,NP為種群規模,每個個體是一個包含D個決策變量xi={xi,1,xi,2,xi,3,…,xi,D}的向量,種群由下面公式產生。 (10) i=1,2,…,NP;j=1,2,…,D, 2.1.2 變異 DE算法主要通過差分策略實現變異過程,這也是區別傳統遺傳算法的重要標志。常用的變異算子為 -rand/1:vi=xr1+F(xr2-xr3), (11) -best/1:vi=xbest+F(xr1-xr2), (12) 式中:整數r1,r2,r3從{1,2,…,NP}中隨機選取,r1≠r2≠r3≠i;尺度因子F從[0,1]之間隨機選擇;xbest為當前子代的最佳個體。 2.1.3 交叉 用二項式交叉算子對變異得到的個體進行交叉操作,即 (13) 式中:jrand為從1到D的整數;CR∈[0,1],為交叉概率。 2.1.4 選擇 采用貪婪算法選擇進入下一代的個體,得到 (14) 上述模型用矩陣表示為 Hβ=T, (15) 為減少隱含層神經元個數,使用差分進化算法優化極限學習機,其流程如圖1所示。 圖1 DE-ELM算法流程圖 VMD具有處理非線性、非平穩信號的優勢,SE具有表征信號特征的能力,可將2種算法相結合用于滾動軸承故障特征提取;而試驗表明DE-ELM在預報命中率、均方根誤差、相關系數方面優于SVM,BPNN及ELM[13];因此,將VMD-SE與DE-ELM相結合用于滾動軸承故障診斷,診斷模型如圖2所示。 圖2 故障診斷模型 通過滾動軸承故障診斷試驗臺(圖3)進行模擬試驗,獲得軸承的振動數據。軸承型號為E3-631,參數見表1;采用2個三軸加速度振動傳感器采集正常狀態、內圈故障、外圈故障、鋼球故障在軸向載荷分別為0(基準載荷),2 750,4 125,5 500,-2 750,-4 125及-5 500 N下(載荷的正負表示在軸向上的2個相反方向)的振動信號;軸承轉速為219 r/min,采樣頻率為5 kHz。振動傳感器的布置如圖3b所示,測點分別在軸截面的12點鐘方位(0號傳感器)和3點鐘方位(1號傳感器)。軸承故障通過電火花刻蝕來實現,分別在內、外圈溝道及鋼球表面上加工寬1.5 mm,深0.4 mm的圓弧形槽進行模擬。各種載荷下的數據均有8列,每列1 500 000個點(為試驗需要,將每列分為300組,每組5 000個數據點)。試驗選擇每種狀態的前20組作為訓練集,后面280組作為測試集。 圖3 滾動軸承試驗臺 表1 滾動軸承主要參數 3.1模態數K的確定 采用中心頻率法[4]確定模態數,由表2可知,K=4時歸一化的中心頻率兩兩之間分隔明顯,因此選擇最佳模態數為4。 表2 不同K值對應的歸一化的中心頻率 為突出VMD的優勢,與LMD進行對比分析,各故障狀態下的前20組樣本熵如圖4所示。從圖中可以看出, VMD與LMD第1個分量的樣本熵區分均比較明顯,但VMD中第2和第3個分量中的內圈故障與外圈故障平均樣本熵差值均大于LMD結果,證明LMD很難分離2個頻率相近的純諧波,也進一步驗證了VMD方法相對于LMD方法對于信號分解的優越性。 圖4 樣本熵分布圖 為體現差分進化算法的優勢,將DE-ELM與傳統ELM以及蝙蝠算法(Bat Algotithm,BA)優化極限學習機[14]進行對比。隱含層節點數對診斷結果存在一定的影響,但并不是節點數越多診斷效果就越好,節點數的增加會導致訓練時間的增加[15]。因此,極限學習機的激勵函數g(x)選用sigmoid函數,設置隱含層節點數為20,40,60,80,100的情況進行對比分析。 不同算法對4種狀態的識別率結果如圖5所示。從圖中可以看出:1)正常狀態下,隨著節點數的增加,ELM的識別率逐漸下降,而BA-ELM,DE-ELM的識別率則一直保持在100%,說明優化算法對正常狀態的識別效果很好;2)內圈故障狀態下,ELM在節點數為80時識別率突然下降到48.57%,而BA-ELM,DE-ELM的識別率依然保持在100%,進一步說明了優化算法的優勢;3)外圈故障狀態下,DE-ELM的識別率依然保持在100%,而BA-ELM識別率最低,僅在節點數為100情況下為72.86%,其他情況為0%,而ELM僅在節點數為40,60情況下達到故障診斷要求;4)鋼球故障狀態下,DE-ELM的識別率隨著節點數的增加略有下降,但依然保持在91%以上,相比BA算法,DE算法更適合改進ELM。 圖5 不同算法的識別率 綜合分析結果可以看到:DE-ELM在節點數為20的情況下識別效果最好,整體識別率高達99%以上。因此,確定最佳節點數為20,也說明了DE-ELM在隱含層節點數較少情況下的優勢。 利用VMD-SE和DE-ELM對直升機滾動軸承進行故障診斷。在VMD分解過程中,利用中心頻率法區分頻率相近的分量,并通過對比試驗驗證了VMD方法的優越性。采用DE算法優化ELM,克服隨機初始化參數影響分類結果的缺點,在隱含層節點數較少情況下有效提高了故障信號的識別率。最后,通過實測真實數據的故障診斷試驗證明了VMD-SE和DE-ELM方法對低速、鋼球多的直升機自動傾斜器滾動軸承故障診斷的有效性。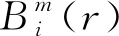
2 DE-ELM算法及故障診斷模型
2.1 差分進化算法
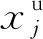
2.2 改進的極限學習機
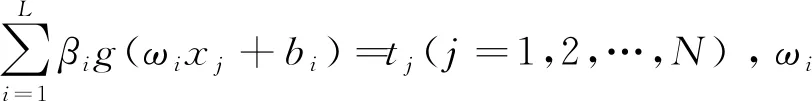
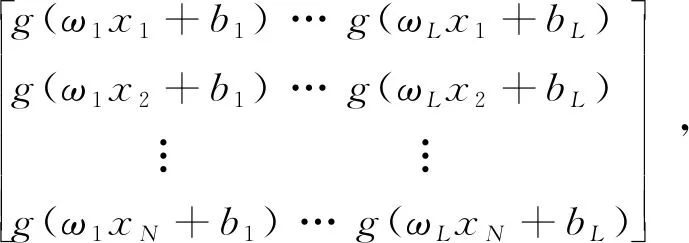
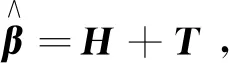
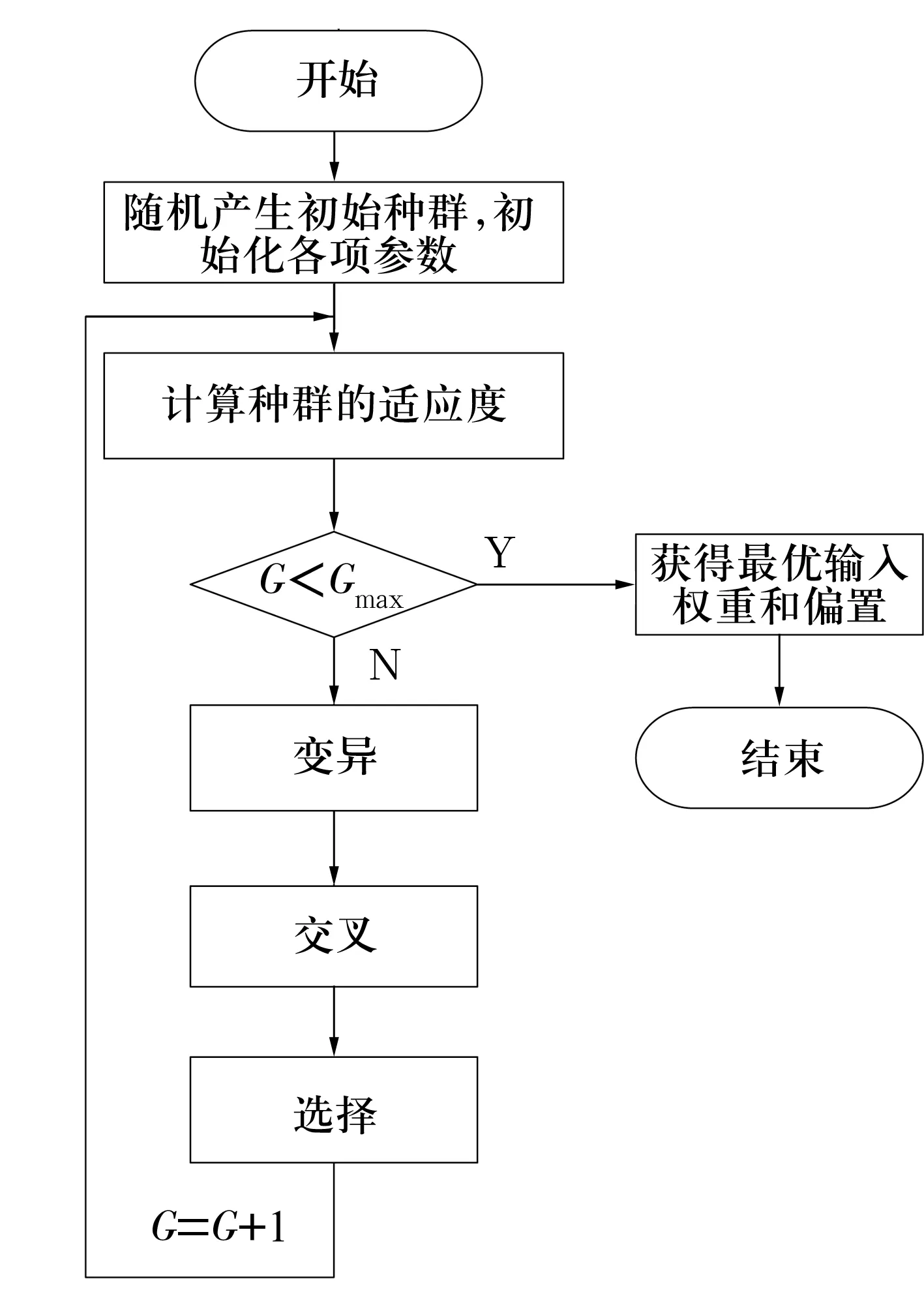
2.3 故障診斷模型
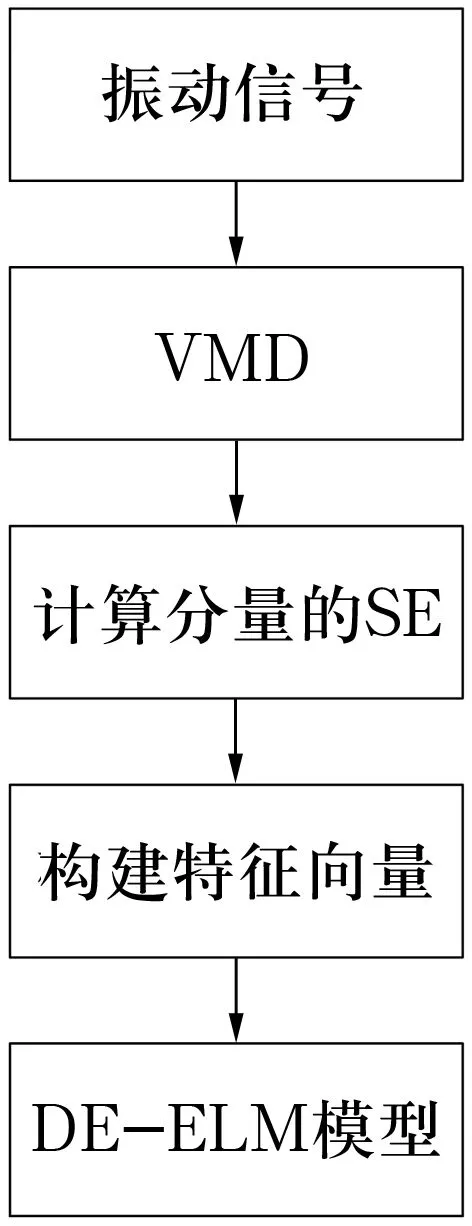
3 應用實例


3.2 故障診斷結果與分析
4 結束語

